Staatsexamenskurs Lineare Algebra
| Website: | WueCampus |
| Kurs: | vhb - lineare Algebra (nicht-vertieft) - Demo |
| Buch: | Staatsexamenskurs Lineare Algebra |
| Gedruckt von: | Gast |
| Datum: | Sonntag, 15. Februar 2026, 10:35 |
1. Lineare Gleichungssysteme, Determinanten- und Matrizenrechnung

Gabriel Cramer (1704 - 1752)
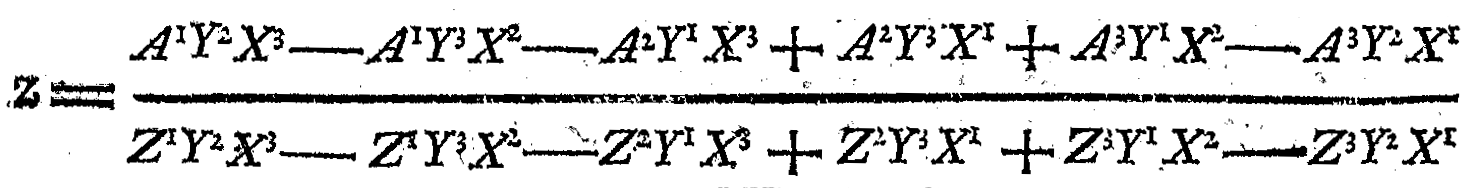
Lineare Gleichungen und Gleichungssysteme finden wir schon 300 v.Chr. sowohl in babylonischen Schriftzeugnissen als auch in China.
Rund zweitausend Jahre später beginnt mit Leibniz (1678), Cramer (1750) und anderen eine intensive Auseinandersetzung mit dieser Problemstellung.
Noch heute übliche Bezeichnungen wie Matrix, Determinante, Existenz und Eindeutigkeit von Lösungen wurden in die Wissenschaft eingeführt.
Sowohl in formaler Hinsicht (Notationen) als auch im Blick auf inhaltliche Erkenntnisse profitiert die Mathematik noch immer von diesen Darstellungen.
1.1. Lineare Gleichungssysteme
In einem ersten Zugang zur Linearen Algebra studieren wir die rechnerischen Grundlagen der Lösung von Linearen Gleichungssystemen. Im Zentrum steht die korrekte und nachvollziehbare Verwendung des Gaußschen Eliminationsverfahrens. Da sich viele Probleme der Linearen Algebra auf ein passendes Lineares Gleichungssystem zurückführen lassen, sind gefestigte Kenntnisse dieser Methode unerlässlich.
kurz nachgedacht
- Bestimmen Sie die Lösungsmenge des nachfolgenden Linearen Gleichungssystems!
\begin{array}{ccccccc}
x_1 & + & x_2 & +& x_3 & = & 9\\
x_1 & + & 2x_2 & + & 5x_3 & = & 15\\
x_1 & + & 3x_2 & + & 8x_3 & = & 23
\end{array}
Lösung - Bestimmen Sie die Lösungsmenge des nachfolgenden Linearen Gleichungssystems!
\begin{array}{ccccccc}
x_1 & + & 2x_2 & + & 3x_3 & = & 0\\
4x_1 & + & 5x_2 & + & 6x_3 & = & 1\\
7x_1 & + & 8x_2 & + & 9x_3 & = & 3
\end{array}
Lösung - Bestimmen Sie die Lösungsmenge des nachfolgenden Linearen Gleichungssystems!
\begin{array}{ccccccc}
x_1 & + & x_2 &&&= &7\\
2x_1 & + & x_2 & + & 2x_3 & = & 5\\
4x_1 & + & x_2 & + & 6x_3 & = & 1
\end{array}
Lösung
Übungsaufgaben
- Sei \(A=\left( \begin{array}{rrrrr}
2 & 3 & 4 & 5 & 9\\
1 & 2 & 3 & 4 & 5\\
1 & 1 & 1 & 1 & 4\\
1 & 0 & -1 & -2 & 3
\end{array} \right), b= \left (\begin{array}{c} 10\\6\\4\\2 \end{array} \right), x=\left(\begin{array}{c} x_1\\x_2\\x_3\\x_4\\x_5\end{array}\right) \)
a) Bestimmen Sie den Lösungsraum des homogenen Linearen Gleichungssystems \(A\cdot x=\vec{0}\).
b) Geben Sie die allgemeine Lösung des Linearen Gleichungssystems \(A\cdot x=b\) an.
Lösung - Gegeben sei \( A=\left( \begin{array}{rrrrr}
1 & 1 & 0 & 1 & 2\\
2 & 1 & 1 & 0 & 3\\
0 & 2 & -2 & 1 & 1\\
-1 & 2 & -3 & 2 & 0\end{array} \right), \text{sowie} \; x_p=\left( \begin{array}{c} 1\\0\\3\\-1\\2 \end{array}\right).\)
a) Bestimmen Sie den Lösungsraum des homogenen Linearen Gleichungssystems \( A\cdot x = \vec{0} \).
b) Bestimmen Sie \( b\in \mathbb{R}^4\) so, dass \(x_p\) eine Lösung von \(A\cdot x = b\) ist und geben Sie die Lösungsmenge dieses Linearen Gleichungssystems an.
Lösung - Sei \( n\in \mathbb{N}, n\geq 2\). Bestimmen Sie die Lösungsmenge \(\mathbb{L}\subset \mathbb{R}^n \) des folgenden Systems von n linearen Gleichungen.
\( \left\{ \begin{array}{l}\sum\limits_{j=1}^kx_j - \sum\limits_{j=k+1}^n=1,\;\; k=1;2;...n-1\\ \sum\limits_{j=1}^nx_j=1\end{array}\right.\)
Lösung - Lösen Sie das inhomogene Lineare Gleichungssystem in Abhängigkeit von \( t\in \mathbb{R} \).
\begin{array}{ccccccc}
2x_1 & + & 3x_2 & + & tx_3 & = & 3\\
x_1 & + & x_2 & - & x_3 & = & 1\\
x_1 & + & tx_2 & + & 3x_3 & = & 2
\end{array}
Lösung
1.2. Determinanten
Ein zentrales Mittel zur Lösung von n Linearen Gleichungen in n Unbestimmten ist die Determinantenberechnung. Bedeutende Mathematiker wie Leibniz, Maclaurin, Bezout und Vandermonde arbeiteten ca. 100 Jahre an dieser Theorie, bis sie die uns heute vertraute Form fand.
Der Wert der Determinante entscheidet (=determiniert), ob das Gleichungssystem eine eindeutige Lösung besitzt oder nicht. Damit ist ein Hilfsmittel an der Hand, das eine qualitative Aussage erlaubt, ohne das System explizit gelöst zu haben.
kurz nachgedacht
- Für \( a,b,c\in \mathbb{R}\) sei
\( A_{a,b,c}=\left(\begin{array}{cccc} a & 1 & b & 2\\
0 & 0 & c & 3\\
1 & 1 & 1 & 1\\
0 & 0 & 1 & 1\end{array}\right) \)
Bestimmen Sie alle \(a,b,c\in \mathbb{R}\), so dass \(\det(A_{a,b,c})\)=0.
Lösung - Berechnen Sie für \(b\in \mathbb{R}\) die Determinante der Matrix
\(\left(\begin{array}{ccc} (b-1)b & 2b & -4\\ 2(b-1)b & 2b & 2\\ 3(b-1)b & b & 6\end{array}\right).\)
Lösung - Beweisen Sie folgende Rechenregeln für Matrizen \(A,B\in M(n\times n,\mathbb{R})\):
(i) \( (A+B)^{\top} =A^{\top}+B^{\top}\)
(ii) \( (A\cdot B)^{\top} = B^{\top}\cdot A^{\top} \)
Lösung
Übungsaufgaben
- Gegeben sei die Matrix
\(B=\left(\begin{array}{ccccc}
0 & 1 & 1 & 1 & 1\\
1 & 0 & 2 & 2 & 2\\
1 & 2 & 0 & 3 & 3\\
1 & 2 & 3 & 0 & 4\\
1 & 2 & 3 & 4 & 0\end{array}\right) \in \mathbb{R}^{5\times 5}\)
a) Man berechne die Determinante von B.
b) Man zeige mit Hilfe von a), dass die Matrix \( C=-\frac{1}{2}B\in \mathbb{R}^{5\times 5}\) die Determinante \(\det C < -1\) besitzt.
c) Man untersuche, ob es eine Matrix \(F\in \mathbb{R}^{5\times 5} \) mit \( F^2=C\) gibt.
Lösung - Gegeben seien die Matrizen:
\(T_1 = (1); T_2=\left(\begin{array}{cc}1 & 1\\1 & 2\end{array}\right); T_3=\left(\begin{array}{ccc} 1 & 1 & 0\\1 & 2 & 1\\0 & 1 & 2\end{array}\right);
T_n=\left(\begin{array}{cccccc}
1 & 1 & 0 & \ldots & \ldots & 0\\
1 & 2 & 1 & 0 & & \vdots\\
0 & 1 & 2 & 1 & \ddots & \vdots\\
\vdots & \ddots & \ddots & \ddots & \ddots & 0\\
\vdots & & \ddots & \ddots & \ddots & 1\\
0 & \ldots & \ldots & 0 & 1 & 2\end{array}\right) \) für \( n\geq 4\)
a) Zeigen Sie mit Hilfe des Determinanten-Entwicklungssatzes die Rekursionsformel
\(\det(T_n)=2\cdot \det(T_{n-1})-\det( T_{n-2})\) für \( n>2.\)
b) Zeigen Sie mit vollständiger Induktion \( \det(T_n)=1\) für alle \(n\in \mathbb{N}.\)
Lösung
1.3. Cramersche Regel
Die Cramersche Regel zur expliziten Berechnung der Lösung eines quadratischen Linearen Gleichungssystem kommt - ohne das Gaußsche Eliminationsverfahren zu verwenden - allein durch Berechnung geeigneter Determinanten zum Ziel.
Dies gelingt allerdings nur (!) bei Systemen, die eine eindeutige Lösung besitzen. Hat das Lineare Gleichungssystem keine eindeutige Lösung, werden wir wieder auf Gauß zurückverwiesen.
Übungsaufgaben
- Ermitteln Sie für welche \(t\in \mathbb{R}\) das inhomogene Lineare Gleichungsystem
\begin{array}{ccccccc}
2x_1 & + & 3x_2 & + & tx_3 & = & 3\\
x_1 & + & x_2 & - & x_3 & = & 1\\
x_1 & + & tx_2 & + & 3x_3 & = & 2\end{array}
eindeutig lösbar ist und berechnen Sie diese Lösung mittels der Cramerschen Regel.
Lösung - Lösen Sie - falls möglich mit Hilfe der Cramerschen Regel - folgendes inhomogenes Lineares Gleichungssystem
\begin{array}{ccccc}
ax_1 & + & bx_2 & = & 2a\\
a^2x_1 & + & b^2x_2 & = & a^2+b^2\end{array}
in Abhängigkeit von \(a;b\in \mathbb{R}\) .
Lösung
Erproben Sie doch zum Abschluss Ihre Kenntnisse in einem Spiel!
1.4. Staatsexamensaufgaben
Herbst 2011 - Thema 3 - Aufgabe 4
a) Bestimmen Sie alle \(t\in \mathbb{R}\), für welche die Determinante der Matrix
\(A=\left(\begin{array}{ccc}
1 & t & t^2\\
t & 2 & t\\
1 & t & 3\end{array}\right) \)
ungleich 0 ist.
b) Bestimmen Sie in Abhängigkeit von \(t\in \mathbb{R}\) alle Lösungen des inhomogenen Linearen Gleichungssystems
\( A\cdot \left(\begin{array}{c} x\\y\\z\end{array}\right)= \left( \begin{array}{c} 1\\2\\1 \end{array}\right)\).
Lösung
Herbst 2012 - Thema 3 - Aufgabe 4
Gegeben sei das Lineare Gleichungssystem \( (G_t)\) über \(\mathbb{R} \):
\( \begin{array}{ccc}
-x+3z & = & 3\\
-2x-ty+z & = & 2\\
x+y+tz & = & 1\end{array} \)
a) Für welche \(t\in \mathbb{R} \) ist \( (G_t)\) eindeutig lösbar?
b) Für welche \(t\in \mathbb{R} \) hat \((G_t)\) keine Lösungen?
c) Für welche \( t\in \mathbb{R} \) hat \( (G_t)\) mehrere Lösungen?
d) Geben Sie in den Fällen der Lösbarkeit die Lösungsmenge von \( (G_t)\) an.
Lösung
Herbst 2019 - Thema 2 - Aufgabe 1
Für \( a\in \mathbb{R} \) sei die reelle Matrix
\( M_a = \left(\begin{array}{cccc}
a & 0 & 1 & 0\\
0 & a & 0 & 1\\
1 & 0 & a & 0\\
0 & 1 & 0 & a\end{array}\right)\in \mathbb{R}^{4 \times 4} \) gegeben.
a) Zeigen Sie, dass die Determinante von \(M_a\) den Wert \( \det M_a= a^4-2a^2+1\) hat.
b) Sei \(b=(1;1;1;1)^{\top}\in \mathbb{R}^4 \). Bestimmen Sie alle \( a\in \mathbb{R}\), für welche die Lösungsmenge \(\mathbb{L}_a=\{ x\in \mathbb{R}^4: M_ax=b\} \) mehr als ein Element hat. Geben Sie in diesem Fall/ diesen Fällen die Lösungsmenge konkret an.
Lösung