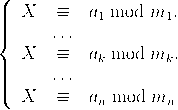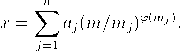3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik
| Site: | WueCampus |
| Cours: | vhb - Grundlagen der elementaren Zahlentheorie (DemoKurs) |
| Livre: | 3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 6 décembre 2025, 05:26 |
Description
Grundlegende Konzepte wie Irrationalität und Primalität werden in diesem Modul behandelt und mit speziellen Methoden wie Kettenbruchentwicklung bzw. Kongruenzkalkül untersucht. Hierbei wird Wert auf eine algorithmische Herangehensweise gelegt, die einen rechnerischen Zugang zur Arithmetik ermöglicht.
______________________________________________________________________________
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.1. Elementare Teilbarkeitslehre
______________________________________________________________________________
|
|
Beispielsweise gelten 
Hierbei ist der Betrag |x| definiert als das Maximum von x und −x. Von diesen vielen Regeln verifizieren wir hier nur (4.): Nach Voraussetzung gelten a = md und b = nd mit gewissen m, n. Dann gilt für beliebige x,y ∈ ℤ zunächst ax + by = mdx + ndy = (mx + ny)d und damit d | (ax + by). |
|
Aufgabe 1. Beweisen Sie die restlichen Rechenregeln zur Teilbarkeit. |
|
Aus Rechenregel (4.) folgt u.a., dass eine ganze Zahl ≠ 0 nur endlich viele Teiler besitzt. Damit besitzen a,b ∈ ℤ, nicht beide gleich Null, einen größten gemeinsamen Teiler ggT(a,b) ∈ ℕ, für den also gilt
Streng genommen ist die Existenz einer solchen Zahl ggT(a,b) hier zu zeigen. Hierzu kann man z.B. wieder mit Hilfe der Wohlordnung argumentieren; die Menge der Teiler d von a und b ist nicht-leer (da 1 | a und 1 | b). Ferner setzen wir ggT(0, 0) = 0. Gilt ggT(a,b) = 1, so nennen wir a und b teilerfremd. Wie so oft starten wir mit einer simplen Tatsache, die sich jedoch als sehr wichtig erweisen wird und deshalb auch einen Namen trägt: |
|
Satz (Division mit Rest). Zu a,b ∈ ℤ mit b ≠ 0 existieren eindeutig bestimmte ganze Zahlen q,r, so dass  |
|
Beweis. Mit dem Prinzip der Wohlordnung besitzt  |
|
Die Aussage des Satzes wird kurz mit ’Division mit Rest’ bezeichnet, weil in    Im Beispiel:  . .Hier nun eine erste wichtige Konsequenz: |
|
Korollar. Für a,b ∈ ℤ mit b ≠ 0 bezeichne d = ggT(a,b). Dann gilt  Der größte gemeinsame Teiler zweier ganzer Zahlen a,b lässt sich also als Linearkombination ax + by von a und b schreiben! |
|
Beweis. Wir nehmen an, dass a ≠ 0 ist (ansonsten ist die zu beweisende Aussage trivial). Wir definieren  |
|
Einige Rechenregeln für den größten gemeinsamen Teiler:
Das kleinste gemeinsame Vielfache zweier ganzer Zahlen a,b ist definiert als das Minimum aller m ∈ ℕ für die a | m und b | m gilt; in Zeichen kgV[a,b]. |
|
Aufgabe 2. Zeigen Sie für beliebige a,b ∈ ℤ die Formel ![ab = ggT (a,b) ⋅ kgV [a,b].](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/744/1ElementareTeilbarkeitslehre9x.gif) |
Den größten gemeinsamen Teiler zweier ganzer Zahlen berechnet man am einfachsten mit dem so genannten euklidischen Algorithmus. Dieses Verfahren entspricht einer sukzessiven Division mit Rest (siehe obigen Satz). |
|
Satz (Euklidischer Algorithmus). Zu gegebenen natürlichen Zahlen a und b mit a > b seien r−1 := a,r0 := b und a = q1b + r1, b = q2 r1 + r2, ... rj-2 = qj rj-1 + rj, ... rn-2 = qn rm-1 + rn, rn-1 = qn+1 rn |
|
Beweis. Die Reste rj sind nicht-negative ganze Zahlen, die in jedem Schritt kleiner werden: 0 ≤ rj < rj−1. Also terminiert der Algorithmus (nach höchstens b Schritten). Durchläuft man das Gleichungssystem von unten nach oben, so zeigt sich rn | rn-1 ⇒ rn|rn-2 ⇒ ... ⇒ rn | r0 = b ⇒ rn | r-1 = a. Damit ist rn ein gemeinsamer Teiler von a und b. Für jeden gemeinsamen Teiler d von a und b ergibt sich beim Durchlauf des Gleichungssystems von oben nach unten sukzessived | a = r-1, d | b = r0 ⇒ d | r1 ⇒ ... ⇒ d | rn-1 ⇒ d | rn.
Also ist rn der größte gemeinsame Teiler von a und b. qed. |
Beispiel des Euklidischen Algorithmus und Spiel zum Euklidischen Algorithmus. Den größten gemeinsamen Teiler bzw. das kleinste gemeinsame Vielfache von mehr als zwei ganzen Zahlen erklärt man induktiv;   |
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.2. Lineare diophantische Gleichungen
___________________________________________________________________________
| Diophantische Gleichungen sind nach dem griechischen Mathematiker Diophantus (ca. 200 v.Chr. - 284 v. Chr.) benannt und spielen insbesondere in der algebraischen Zahlentheorie eine wichtige Rolle. Unter einer derartigen Gleichung versteht man eine polynomielle Gleichung mit ganzzahligen Koeffizienten bei der man sich insbesondere für die ganzzahligen Lösungen interessiert. Derartige Gleichungen haben häufig einen realen Bezug, so treten sie beispielsweise in der Chemie oder bei der Gewichteverteilung bei Balkenwaagen auf. |
|
Wir starten bescheiden mit einer linearen Gleichung in zwei Unbekannten  Gibt es also ganzzahlige Lösungen der obigen Gleichung? Angenommen, a und b sind nicht teilerfremd, also ggT(a,b) > 1, dann ist nach dem Korollar aus III.1. ax + by für beliebige ganzzahlige x,y stets ein Vielfaches von ggT(a,b) und also nie gleich eins; in diesem Fall ist die Gleichung also unlösbar. Sind jedoch a und b teilerfremd, also ggT(a,b) = 1 (gleich der rechten Seite), dann ist die Gleichung wiederum nach dem Korollar aus III.1. lösbar. Es ist gut zu wissen, wann diese Gleichung lösbar ist, aber im Falle ihrer Lösbarkeit ist es in der Praxis oft darüber hinaus sehr hilfreich, auch noch eine Lösung (oder gar alle) zu kennen. Unser bisheriges Argument reicht an dieser Stelle leider nicht aus, wohl aber hilft hier der euklidische Algorithmus aus dem vorhergehenden Kapitel weiter. Besonders gut lässt sich dies mit Hilfe eines Beispiels illustrieren. |
|
Aufgabe 1. Bestimmen Sie die Menge aller ganzzahligen Lösungen der linearen Gleichung  |
| Eine wichtige Verallgemeinerung unserer bisherigen Überlegungen (insbesondere des Korollars aus III.1.) liefert der |
|
Satz (Satz von Bézout). Die lineare Gleichung
mit ganzen Zahlen a,b,c ist genau dann ganzzahlig lösbar, wenn ggT(a,b) ein Teiler von c ist; in diesem Fall ist die Menge der ganzzahligen Lösungen gegeben durch
|
|
Beweis. Nach Obigem sind die Gleichungen (2) bzw. (3) ganzzahlig lösbar. Falls ggT(a,b) ein Teiler von c ist, d.h. c = dggT(a,b) für ein d ∈ ℤ, so ist mit einer Lösung x,y von (3) dann dx,dy eine Lösung der Gleichung:  Dank des euklidischen Algorithmus lässt sich die Lösungsgesamtheit wie folgt beschreiben: Gegeben eine spezielle ganzzahlige Lösung x0,y0 von (2), so ist insbesondere ggT(a,b) ein Teiler von c und jede Lösung von (1) ist – wie man sofort nachrechnet – von der Form
Der Satz ist somit vollständig bewiesen. qed. |
| Die ganzzahligen Lösungen einer linearen diophantischen Gleichung sind auch hinsichtlich der rationalen Approximation sehr interessant, siehe hierfür wiederum ein illustrierendes Beispiel. |
______________________________________________________________________________
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3. Approximation mit Kettenbrüchen
_______________________________________________________________
| In diesem Kapitel werden zunächst Kettenbrüche erklärt und anschließend die Approximation reeller Zahlen mit Kettenbrüchen beschrieben. |
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3.1 Approximationssatz von Dirichlet
_______________________________________________________________
| Die Menge ℚ liegt dicht in der Menge ℝ, d.h. in jeder noch so kleinen Umgebung einer beliebigen reellen Zahl gibt es eine (tatsächlich sogar unendlich viele) rationale Zahl(en). Insofern macht es Sinn, reelle Zahlen durch rationale approximieren zu wollen, aber wie macht man das? |
| Eine wichtige Frage ist dabei, wann eine rationale Zahl überhaupt eine gute rationale Approximation genannt werden sollte? Eine mögliche Antwort hierauf liefert der folgende |
| Satz (Approximationssatz von Dirichlet, 1842). Zu einer Irrationalzahl α gibt es unendlich viele rationale Zahlen p/q mit |
|
Beweis. Wir notieren den Ganzteil und den gebrochenen Anteil einer reellen Zahl x als 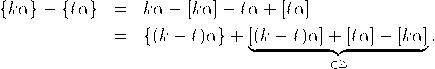 Weil nun {kα}−{ℓα} in dem Intervall [0,1/Q) liegt, addieren sich die Ganzteile in der vorangegangenen Formel zu null auf. Sei nun q = k − ℓ, dann gilt also {qα} = {kα}−{ℓα} <1/Q. Mit p := [qα] folgt ferner welches wegen q < Q die gewünschte Abschätzung liefert. Jetzt nehmen wir an, dass α irrational ist und nur endlich viele p1/q1,…,pn/qn der gewünschten Ungleichung genügen. Mit der Irrationalität von α gibt es dann ein Q mit |α −pj/qj| >1/Q für j = 1,…,n, was der oberen Abschätzung gegen 1/(qjQ) widerspricht. Damit ist der Satz bewiesen. qed. |
|
Der Beweis des Dirichletschen Approximationssatzes zeigt leider nicht, wie zu einer gegebenen Irrationalzahl wirklich gute rationale Approximationen tatsächlich gefunden werden können. Tatsächlich charakterisiert die Approximationseigenschaft des Dirichletschen Approximationssatzes Irrationalzahlen: |
Satz. Für rationale Zahlen α gibt es nur endlich viele rationale Zahlen p/q mit
![]()
| Die Frage, ob eine gegebene reelle Zahl α irrational ist, lässt sich also durch die Qualität rationaler Näherungen beantworten. Im Falle eines irrationalen α existieren unendlich viele p/q, die um weniger als 1/q2 von α abweichen, während für rationale α nur endlich viele solche existieren. |
| Beweis. Ist α = m/n mit teilerfremden m,n und m/n ≠ p/q, so gilt |
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3.2. Kettenbrüche
_______________________________________________________________________________
|
|
Zunächst betrachten wir den euklidischen Algorithmus, welchen wir (gemäß der Notation aus III.1.) umschreiben als (1) für n ≤ m; dabei steht ⌊x⌋ für die größte ganze Zahl ≤ x (auch Gaußklammer bzw. Ganfteil genannt). Setzen wir an = ⌊rn−1/rn⌋, so ergibt sich
Der typographische Albtraum 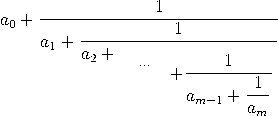 heißt Kettenbruch (engl. continued fraction); die an nennt man Teilnenner. Wir notieren einen solchen Kettenbruch kurz mit ![[a ,a ,a ] = a2a1a0 +-a2-+-a0-. 0 1 2 a2a1 + 1](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch5x.gif)
und ![[a0,a1,...,an] = a0 + ----1------= [a0,[a1,...,an]]. [a1,...,an ]](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch7x.gif) Für n ≤ m nennen wir [a0,a1,…,an] den n-ten Näherungsbruch an [a0,a1,…,am]. Wir definieren desweiteren 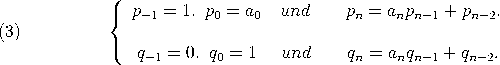 Die Berechnung der Näherungsbrüche erfolgt leicht mit Hilfe von |
Satz. Für 0 ≤ n ≤ m gilt
![pn-= [a0,a1,...,an]. qn](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch9x.gif)
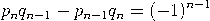
|
Beweis per Induktion nach n. Der Fall n = 0 ist trivial. Der Fall n = 1 folgt unmittelbar aus ![a1a0 + 1 p1 [a0,a1] = ---------= --. a1 q1](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch11x.gif) ![[ ] --1-- [a0, a1,...,an,an+1] = a0,a1,...,an + an+1 .](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch12x.gif) 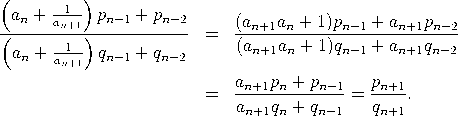 was die Induktion und den Beweis der ersten Aussage abschließt. Mittels (3) ist 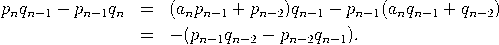 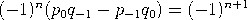 |
Jetzt weisen wir den Teilnennern an und somit auch dem Kettenbruch [a0,a1,…,am] numerische Werte zu. Wir fordern a0∈ℤ und an∈ℕ für 1 ≤ n < m, sowie am≥ 1. Sei jetzt α irgendeine rationale Zahl. Dann gibt es teilerfremde ganze Zahlen a und b > 0, so dass α = ab. Es folgt aus der Variation des euklidischen Algorithmus (1) angewandt auf r−1 = a und r0 = b, dass α als endlicher Kettenbruch dargestellt werden kann: ![[ ] a-= [a0,a1,a2,...,am ] , wobei an = rn−1-. b rn](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch16x.gif) ![[a0,a1,a2,...,am ] = [a0,a1,a2, ...,am − 1,1];](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch17x.gif) Jetzt wollen wir Kettenbrüche zu nicht notwendig rationalen Zahlen bilden. Wir können den Algorithmus (1) zur Berechnung der Kettenbruchentwicklung von rationalen Zahlen umschreiben als
Setzen wir an = ⌊αn⌋, so erhalten wir α = [a0,a1,…,an,αn+1]. Dieser Algorithmus ist der Kettenbruchalgorithmus. Ist α rational, dann bricht die Iteration nach endlich vielen Schritten ab und der Kettenbruchalgorithmus ist nichts anderes als der euklidische Algorithmus in Verkleidung. Beispiel. ![[a ,a ,...] := lim [a ,a ,...,α ]. 0 1 m→ ∞ 0 1 m](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch19x.gif) |
|
Satz. Sei α = [a0,a1,…,an,αn+1] irrational mit Näherungsbrüchen pn/qn. Dann gilt 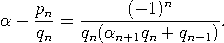
und ![pn α = lim ---= [a0,a1,a2,...]. n→∞ qn](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch22x.gif) |
|
Beweis. Zunächst bemerken wir, dass alle unsere Beobachtungen über endliche Kettenbrüche sich auf unendliche Kettenbrüche übertragen - insbesondere (3) und der vorherige Satz. Eine kurze Berechnung zeigt 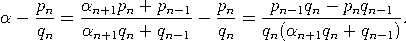 Der vorherige Satz impliziert damit die erste Behauptung. Wegen an+1≤ αn+1 folgt ferner 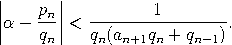 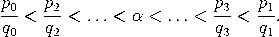 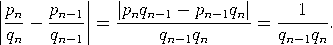 |
Sehr interessant sind auch so genannte periodische Kettenbrüche. |
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3.3. Gesetz der besten Approximation
|
|
Gegeben zwei reelle Zahlen α = [a0,…,an,αn+1] und α' = [a0,…,an,αn+1'] mit denselben ersten Teilnennern, dann folgt, dass jedes α'', das zwischen α und α' liegt, eine Kettenbruchentwicklung besitzt, die mit denselben Teilnennern startet, wie die von α und α', nämlich: ![α'' = [a ,...,a ,α '' ] 0 n n+1](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/741/23Beste0x.gif) Der zweite Satz aus dem vorherigen Kapitel zeigt, wie wichtig Kettenbrüche in der Theorie der diophantischen Approximation sind. Es folgt nämlich unmittelbar: Ist α = [a0,a1,…] irrational mit Näherungsbrüchen pn/qn, dann gilt 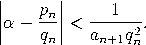 Diese Beobachtung ist kein Wunder wie Lagrange 1770 bewiesen hat: |
|
Satz (Gesetz der besten Approximation). Sei α irgendeine reelle Zahl mit Näherungsbrüchen pn/qn. Ist n ≥ 2 und sind p,q natürliche Zahlen mit 0 < q ≤ qn und p/q ≠ pn/qn, so gilt  |
| Das Gesetz der besten Approximation besagt also, dass die besten rationalen Approximationen durch die Näherungsbrüche der Kettenbruchentwicklung gegeben sind. Dies lässt sich an Beispielen veranschaulichen - ein besonders Prominentes ist unser täglich verwendetes Papierformat Din-A. |
|
Beweis. Wir dürfen annehmen, dass p und q teilerfremd sind. Wegen 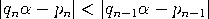 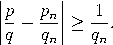 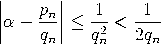 , ,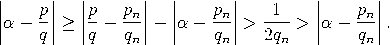 Es verbleibt der Fall: qn−1< q < qn. Das lineare Gleichungssystem 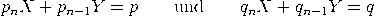 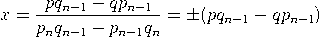 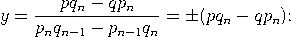 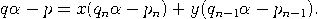 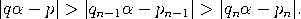 |
|
Eine Irrationalzahl α heißt quadratisch irrational, falls sie Wurzel eines quadratischen Polynoms mit ganzzahligen Koeffizienten ist; da α irrational ist, ist das Polynom irreduzibel (d.h. nicht als Produkt zweier linearer Polynome mit rationalen Koeffizienten darstellbar). Jede relle quadratische Irrationalität lässt sich also darstellen als
wobei a,b ∈ ℤ, c,d ∈ ℕ. Dies ergibt sich unmittelbar durch das Lösen der zu Grunde liegenden quadratischen Gleichung. Alle Beispiele dieser quadratischen Irrationalitäten haben folgendes gemein: Ihre Kettenbruchentwicklung ist periodisch! Hierbei heißt ein Kettenbruch [a0,a1,…] periodisch, falls es einen Index ℓ gibt, so dass an+ℓ = an für alle hinreichend großen n. Wir schreiben ![-------------- [a0,a1, ...,ar,ar+1,...,ar+ℓ] = [a0,a1,...,ar,ar+1,...,ar+ ℓ,ar+1,...,ar+ ℓ,...];](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/741/23Beste13x.gif)
wobei a1,a2,…,a2,a1 ein Palindrom ist. Dies wurde von Galois bewiesen, der tragisch in einem Duell verstarb und trotz seines jungen Alters unsterblich für die Algebra und Zahlentheorie ist. Wir verzichten hier auf den Beweis. |
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.4. Primzahlen
_______________________________________________________________________________| Primzahlen sind die multiplikativen Bausteine der ganzen Zahlen, da jede ganze Zahl in Primzahlen faktorisiert werden kann. Diese Faktorisierung ist bei großen Zahlen zumeist sehr aufwendig und es gibt noch kein effizientes Faktorisierungsverfahren. Diese Schwierigkeit wird bei modernen Verschlüsselungsverfahren oft ausgenutzt. Überhaupt haben Primzahlen eine sehr prominente Stellung im Alltag und in der Mathematik. |
|
Eine natürliche Zahl n > 1 heißt Primzahl oder kurz prim, wenn sie nur durch sich selbst und 1 teilbar ist (innerhalb der Menge ℕ); ansonsten nennt man n zusammengesetzt. Die ’ersten’ Primzahlen findet man leicht:  |
|
Lemma (Lemma von Euklid). Teilt eine Primzahl p ein Produkt, so teilt sie mindestens einen der Faktoren:  |
| Beim Beweis dürfen wir natürlich kein Ergebnis verwenden, welches wir mit Hife des Euklidschen Lemmas bewiesen haben, ansonsten entstünde ein ’Zirkelschluss’ und nichts wäre wirklich bewiesen. |
|
Beweis. Angenommen, p ∤ a, also insbesondere ggT(p,a) = 1 (da p eine Primzahl ist). Nach dem Korollar aus III.1. existieren ganze Zahlen x,y mit  |
|
Die Aussage des euklidschen Lemmas ist falsch für zusammengesetzte Zahlen: Beispielsweise teilt 6 das Produkt 2 ⋅ 3, jedoch keinen der Faktoren. Insofern charakterisiert das Lemma von Euklid also Primzahlen! Man überlege sich, wo genau im Beweis davon Gebrauch gemacht wurde, dass p eine Primzahl ist und warum das so entscheidend ist? Wir haben schon die multiplikative Zerlegbarkeit ganzer Zahlen in Primfaktoren angesprochen. Diese ist sogar eindeutig. So simpel dieser Sachverhalt auch sein mag, diese Beobachtung bildet einen der wichtigsten Sätze der Zahlentheorie überhaupt! Die entsprechende Aussage hätte eigentlich bereits in Euklids Elementen stehen können, jedoch findet man sie erst bei Gauß in seinen berühmten ’Disquisitiones Arithmeticae’ aus dem Jahre 1801. |
|
Satz (Fundamentalsatz der Arithmetik). Jede natürliche Zahl n besitzt eine eindeutige Primfaktorzerlegung, d.h. es gibt eindeutig bestimmte Exponenten νp(n) ∈ℕ0, so dass
|
| Hierbei läuft das Produkt über alle Primzahlen; tatsächlich sind stets jedoch nur endlich viele Exponenten νp(n) verschieden von Null. Für n = 1 verschwinden alle Exponenten und das Produkt ist leer. |
|
Beweis. Wir nutzen die Wohlordnung von ℕ. Wir zeigen zunächst die Existenz: Ist n ∈ℕ die kleinste Zahl, für die eine solche Primfaktorzerlegung nicht bekannt ist, so ist n entweder prim oder ein Produkt kleinerer natürlicher Zahlen, für die die Aussage bereits bekannt ist. Also folgt die Existenz einer Primfaktorzerlegung von n. Nun der Nachweis der Eindeutigkeit: Angenommen, n ist minimal mit zwei wesentlich verschiedenen Primfaktorzerlegungen,
|
| Wie reichhaltig ist die Menge der multiplikativen Bausteine der ganzen Zahlen? Eine erste Antwort auf diese Frage gibt ein berühmtes Resultat von Euklid (was heutzutage bereits in der Schule gelehrt wird): |
|
Satz (Euklid). Es gibt unendlich viele Primzahlen. |
|
Beweis. Wir zeigen: Zu jeder gegebenen endlichen Menge von Primzahlen existiert eine weitere; damit ist die Menge der Primzahlen also nicht endlich! Sei hierzu p1 = 2,p2,…,pm eine Menge von Primzahlen. (Hierbei haben wir p1 explizit mit dem Wert 2 belegt, damit wir nicht mit einer leeren Primzahlmenge argumentieren!) Dann ist die natürliche Zahl
Mit q und q − 1 würde dann aber p auch jede Linearkombination dieser beiden Zahlen teilen (4. Rechenregel aus III.1.), also insbesondere |
| Der Beweis liefert ein Beispiel dafür, zu einer gegebenen Liste von Primzahlen weitere zu finden. Die Unendlichkeitsaussage von Euklid gibt nur eine unzulängliche Beschreibung für die Primzahlen. Auf den ersten Blick scheinen die Primzahlen wie zufällig aufzutreten, aber gehorcht ihre Verteilung vielleicht doch einer bestimmten erstaunlichen Gesetzmäßigkeit. Ein klassische Fragestellung der Zahlentheorie lautet deshalb: Wie sind die Primzahlen innerhalb der natürlichen Zahlen verteilt? Veranschaulichen lässt sich diese Frage beispielsweise durch die sogenannte Ulam-Spirale. |
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.5. Rechnen mit Restklassen
__________________________________________________________________________
| Eine zahlentheoretische Besonderheit bildet das Rechnen mit sogenannten Restklassen. Eine besonders spannende Anwendung hierfür ist beispielsweise das Verschlüsselungsverfahren RSA. |
Zunächst soll das Rechnen mit Restklassen eingeführt werden. Sei hierzu m eine natürliche Zahl, so definiert   Kongruenzen sind eine Verallgemeinerung von Gleichungen, denn mit a = b gilt sicherlich auch a ≡ b mod m für jedes beliebige m ∈ ℕ. Insbesondere bestehen folgende Rechenregeln: Für beliebige a,b,c,d ∈ ℤ und m ∈ ℕ gelten
Die ersten drei Rechenregeln reflektieren, dass es sich bei der Kongruenz um eine Äquivalenzrelation handelt (s.o.). Von den restlichen Rechenregeln beweisen wir hier nur die 6. Rechenregel: Nach Voraussetzung gilt m∣(a − b)c und weil ggT(m,c) sowohl m als auch c teilt, folgt  Wir schreiben die Äquivalenzklassen bzgl. ∼ als     Mit a ≡ A und b ≡ B mod m existieren per Definition ganze Zahlen k,ℓ mit a = A + km und b = B + ℓm, so dass (a mod m) + (b mod m) = (a + b) mod m
= (A + B + (k + ℓ)m) mod m
= (A + B) mod m = (A mod m) + (B mod m). Nun betrachten wir sämtliche Restklassen eines festen Moduls gemeinsam. Modulo m bilden die Restklassen   Diese Strukturen sind kein Zufall |
|
Satz. Sei m eine natürliche Zahl, dann ist die Menge ℤ∕mℤ mit der oben definierten Addition und Multiplikation ein kommutativer Ring, der sogenannte Restklassenring modulo m. |
|
Beweis. Die Menge ℤ∕mℤ ist mit der oben eingeführten Addition eine abelsche Gruppe mit neutralem Element 0 mod m bzgl. der Addition (was sich aus unseren bisherigen Überlegungen unmittelbar ergibt). Mit der oben definierten Multiplikation ist ℤ∕mℤ eine Halbgruppe und 1 mod m ist das neutrale Element der Multiplikation, insbesondere gelten die Distributiv- und Assoziativgesetze. Damit ist ℤ∕mℤ ein Ring und der Satz bewiesen. qed. |
|
Die Idee der Restklassenbildung ist oft hilfreich, um redundante Information los zu werden, mit dem Vorteil von der unendlichen Menge ℤ zur endlichen Menge von Restklassen modulo m übergehen zu können. Die Restklassenarithmetik hat ganz verschiedene Anwendungen, wie beispielsweise bei ISBN-Nummern. Eine Restklasse a mod m heißt prim, wenn a und m teilerfremd sind. Wegen ggT(a + km,m) = ggT(a,m) ist entweder jedes Element einer Restklasse oder keines teilerfremd zum Modul m. Die primen Restklassen modulo m = 8 sind damit  φ(8) = 4, φ(10) = 4 und φ(2k) = 2k+1 bzw.φ(p) = p-1 und φ(pk) = pk(1 - 1/p) für p prim. Die Idee der primen Restklassen (bzw. multiplikativ Inversen) hilft auch beim Lösen von linearen Kongruenzen. Diese Idee lässt sich verallgemeinern |
|
Satz. Seien a,b ∈ ℤ und m ∈ ℕ. Dann ist die Kongruenz  |
|
Beweis. Nach dem Satz von Bézout ist die lineare diophantische Gleichung   |
| Der Beweis ist konstruktiv (dank des euklidischen Algorithmus versteckt im Satz von Bézout). In einem alten chinesischen Mathematikbuch vor ca. zweitausend Jahrhen stellte sein Verfasser Sun-Tsu folgende Aufgabe: |
|
Aufgabe 1. Finde eine Zahl, welche Zahl bei Division durch 3 den Rest 2, bei Division durch 5 den Rest 3 und bei Division durch 7 den Rest 2 lässt. |
| Hierher rührt auch der Name des folgenden Resultates: |
|
Satz (Chinesischer Restsatz). Es seien m1,…,mn ∈ ℕ paarweise teilerfremd und a1,…,an ∈ ℤ beliebig. Dann besitzt das lineare Konruenzsystem
|
| Eine interessante Interpretation des chinesischen Restsatzes ist die folgende: In einem hinreichend kleinen Intervall ist eine ganze Zahl also eindeutig durch ihre Reste modulo kleiner Primzahlen bestimmt! |
|
Beweis. Wir haben die Existenz und die Eindeutigkeit dieser Lösung zu zeigen. Hierzu setzen wir
Also gilt x ≡ ak mod mk für 1 ≤ k ≤ n und x ist eine Lösung unseres linearen Kongruenzsystems. Dies beweist also die Existenz einer Lösung; nun der Nachweis der Eindeutigkeit: Eine Restklasse y ist genau dann eine Lösung, wenn mj∣(x − y) für 1 ≤ j ≤ n gilt. Mit der paarweisen Teilerfremdheit der mj ist dies äquivalent zu m = m1⋅…⋅mn∣(x−y) bzw. x ≡ y mod m, was zu zeigen war. qed. |
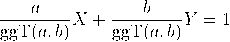
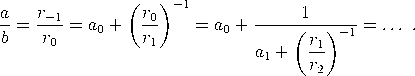
![[ ] [a ,a ,...,a ] = a ,a ,...,a + -1- 0 1 n 0 1 n−1 an](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/743/22Kettenbruch6x.gif)
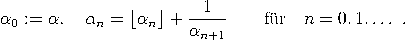
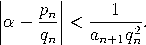
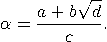
![[[ ] ------------------[---]] √ -- √ -- √ -- d = d ,a1,a2,...,a2,a1,2 d ,](https://wuecampus.uni-wuerzburg.de/moodle/pluginfile.php/114950/mod_book/chapter/741/23Beste14x.gif)