1. Trigonometrie I

1.4. Bestimmung einiger Funktionswerte und Zusammenhänge zwischen Sinus, Kosinus und Tangens

Bestimmung einiger Funktionswerte und Zusammenhänge zwischen Sinus, Kosinus und Tangens

Nach der Einführung von Sinus, Kosinus und Tangens (am rechtwinkligen Dreieck) sollten einige Funktionswerte exakt bestimmt und Zusammenhänge zwischen Sinus, Kosinus und Tangens herausgearbeitet werden. Das ist u. a. auch deshalb sinnvoll, da die Schülerinnen und Schüler hierbei immer wieder auf die Definitionen zurückgreifen müssen. Außerdem werden Unterrichtsinhalte früherer Jahre (z. B. Innenwinkelsatz, Satz des Pythagoras) wiederholt. Vor allem aber erfolgt eine Vernetzung geometrischer Überlegungen mit algebraischen Herleitungen.

Exakte Bestimmung einiger Funktionswerte

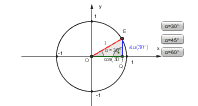
Erarbeiten Sie die Werte für den Sinus und den Kosinus der Winkelbeträge 30°, 45° und 60°.

Eine Hilfe erhalten Sie im Applet rechts.


Hilfe Funktionswerte

Zusammenhänge zwischen Sinus, Kosinus und Tangens

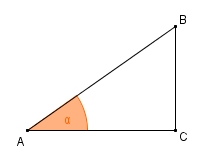
Zeigen Sie durch geometrische Überlegungen folgende Zusammenhänge:

  1. \( \sin (90^\circ – \alpha) = \cos \alpha\) und \( \cos (90^\circ – \alpha) = \sin \alpha\)
  2. \( \tan \alpha =\frac{\sin \alpha }{\cos \alpha }\)
  3. Trigonometrischer Satz des Pythagoras für alle rechtwinkligen Dreiecke: \[ \sin^2 \alpha + cos^2 \alpha = 1\] (verkürzte Schreibweise \(\sin^2 α\) für \((\sin \alpha)^2 \))

Hilfe Zusammenhang