Demokurs: Didaktik der Geometrie

Startsida:	WueCampus
Kurs:	vhb - Demokurs Lehramt
Bok:	Demokurs: Didaktik der Geometrie

Utskrivet av:	Visiteur anonyme
Datum:	fredag, 17 maj 2024, 04:32

Beskrivning

Kursbuch

Innehållsförteckning

1. Trigonometrie I

1. Trigonometrie I

Trigonometrie I – Einstiege in die Trigonometrie

Im Kapitel Trigonometrie I – Einstiege in die Trigonometrie finden Sie:

Die Gegenüberstellung zweier möglicher Unterrichtseinstiege in die Trigonometrie.

Diese werden dann genauer ausgeführt:

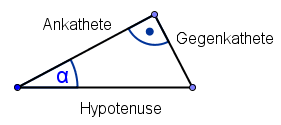
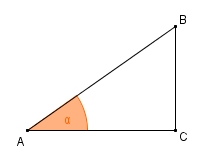
Einführung von Sinus und Tangens am rechtwinkligen Dreieck.
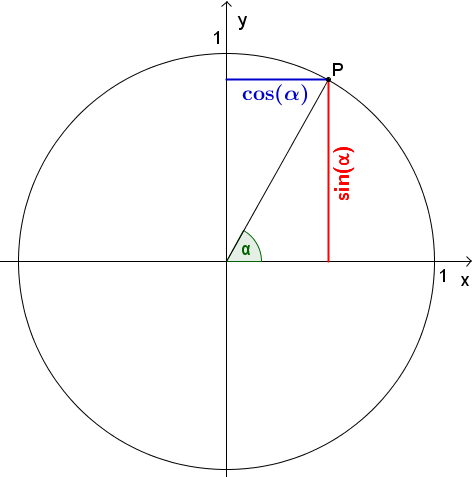
Sinus, Kosinus und Tangens am Einheitskreis.

Nach der Einführungssequenz sollen

einige Funktionswerte exakt bestimmt und Zusammenhänge zwischen Sinus, Kosinus und Tangens erarbeitet werden.

Bedeutung für den Geometrieunterricht

Das Wort Trigonometrie kommt aus dem Griechischen und bedeutet Dreiecksmessung. Das Dreieck nimmt eine sehr wichtige Rolle in der Geometrie ein und somit auch die Trigonometrie im Geometrie- bzw. gesamten Mathematikunterricht. Für die zentrale Bedeutung der Dreiecksbetrachtungen in der Geometrie gibt es mehrere Gründe: Jedes beliebige Vieleck lässt sich in Dreiecke zerlegen, so dass man zu Berechnungen am Vieleck auf Dreiecksberechnungen zurückgreifen kann. Unter anderem dadurch ergibt sich die Bedeutung der Dreiecke für das Lösen geometrischer Probleme.

Zudem hat das Unterrichtsthema Trigonometrie Berührungspunkte zu besonders vielen Leitideen ("Raum und Form", "Messen", "funktionaler Zusammenhang" und "Zahl") und das Thema bietet viele Möglichkeiten für Anwendungen, Modellierungen und Vernetzungen. Die Zusammenhänge zwischen Geometrie und Algebra treten besonders deutlich hervor, wenn geometrische Aufgaben, die vorher nur konstruktiv gelöst werden konnten nun algebraisch gelöst werden.

Für die Wahl eines geeigneten Einstiegs in die Behandlung der Trigonometrie ist neben der Wahl geeigneter Anwendungskontexte vor allem die Frage zu berücksichtigen, wie an frühere Inhalte des Unterrichts angeknüpft werden kann.

1.1. Einstiege in die Trigonometrie

Einstiege in die Trigonometrie

Für die unterrichtliche Einführung der Trigonometrie werden besonders zwei mögliche Einstiege diskutiert:

Die Definition von Sinus, Kosinus und Tangens am rechtwinkligen Dreieck und
die Einführung von Sinus und Kosinus am Einheitskreis.

Die folgende Gegenüberstellung der beiden Methoden macht unter anderem die jeweiligen Vor- und Nachteile deutlich:

1. Einführung über rechtwinklige Dreiecke

Bei diesem Einstieg werden Sinus, Kosinus und Tangens zunächst nur für den Spezialfall spitzer Winkel am rechtwinkligen Dreieck definiert. Eine Erweiterung für beliebige Winkel erfolgt erst später, z.B. am Einheitskreis.

Vorteile
Bei dieser Einführung stehen Berechnungen an geometrischen Figuren von Anfang an im Mittelpunkt und es ergeben sich vielfältige Anknüpfungspunkte an frühere Unterrichtsinhalte und somit das Vorwissen der Lernenden. Es finden sich vielfältige Problemstellungen und Anwendungen, aus denen heraus Sinus, Kosinus und Tangens entwickelt werden können. Über diesen Einstieg ergibt sich zudem die Möglichkeit einer genetischen Einbettung der Geometrie in den Mathematikunterricht.

Nachteile
Für eine Verallgemeinerung auf beliebige Winkelgrößen sind zusätzliche Überlegungen notwendig, die Zeit erfordern.

Definition von Sinus, Kosinus und Tangens am rechtwinkligen Dreieck

Genetischer Unterricht

2. Einführung am Einheitskreis

Bei diesem Einstieg werden Sinus und Kosinus für beliebige Winkelgrößen am Einheitskreis definiert. Anschließend kommt es zur Anwendung auf rechtwinklige Dreiecke.

Vorteile
Bei dieser Einführung können Sinus und Kosinus sofort für beliebige Winkel definiert werden. Zudem wird die Leitidee "funktionaler Zusammenhang" betont und der Übergang zu den Graphen der Sinus- und Kosinusfunktion liegt sehr nahe (Trigonometrische Funktionen).

Nachteile
Es gibt für diesen Einstieg wenige Anknüpfungspunkte an frühere Unterrichtsinhalte, weshalb er für die Schülerinnen und Schüler schwer zu motivieren ist.

Definition von Sinus, Kosinus am Einheitskreis

In den folgenden zwei Unterkapiteln werden die beiden Einstiege genauer vorgestellt.

1.2. Einführung von Sinus, Kosinus und Tangens am rechtwinkligen Dreieck

Einführung von Sinus, Kosinus und Tangens am rechtwinkligen Dreieck

Meistens wird in den Lehrbüchern zuerst der Sinus eingeführt, in manchen wird aber auch mit dem Tangens begonnen (was sinnvoll erscheint, da die Frage nach dem Zusammenhang zwischen Anstieg (Steigung) und Steigungswinkel bereits seit der Behandlung der linearen Funktionen offen ist).

Zum Einstieg in die Trigonometrie am rechtwinkligen Dreieck sollten zunächst Anwendungsprobleme gewählt werden, die bereits in früheren Schuljahren durch maßstäbliche Darstellungen konstruktiv bearbeitet werden konnten. Derartige Anwendungen können nun die exakte rechnerische Bestimmung fehlender Größen in rechtwinkligen Dreiecken motivieren.

Im Folgenden werden zwei Anwendungssituationen vorgestellt, welche die Einführung von Sinus und Tangens motivieren können:

Anwendungssituation zur Einführung des Sinus: Der Kran

Der Ausleger eines Krans sei 9,5 m lang und kann bis auf eine Länge von 35 m ausgefahren werden. Man kann ihn bis zu einem Winkel von höchstens 80° gegen die Waagerechte aufrichten. Mit Hilfe des Winkels und der Länge des Auslegers kann die Tragkraft des Krans kalkuliert und die Hubhöhe eingestellt werden, um die die Last angehoben werden kann.

Machen Sie sich mit Hilfe des Applets mit der Bedienung des Krans in Bezug auf die Hubhöhe vertraut. Von welchen Größen ist sie abhängig?

Anwendungssituation zur Einführung des Tangens: Straßensteigung

Straßensteigungen und -gefälle werden auf Verkehrsschildern in Prozent angegeben. Als steilste Straße der Welt gilt die Baldwin Street in Neuseeland mit einer maximalen Steigung von ca. 35%. Automobilkonzerne werben damit, dass ihre PKW-Topmodelle 80 oder sogar 100 Prozent Steigung bewältigen können.

Machen Sie sich mit Hilfe des Applets mit dem Begriff Steigung vertraut und erklären Sie, wie die Angabe von z.B. 80% entstehen kann.

Nach der Diskussion einführender Beispiele sollten die Verhältnisse in rechtwinkligen Dreiecken weiter erkundet bzw. gesichert werden, bevor die Begriffe Sinus, Kosinus und Tangens eingeführt werden:

Im zweiten Schritt muss die Erkenntnis gewonnen bzw. gesichert werden, dass in einem rechtwinkligen Dreieck das Verhältnis zweier Seitenlängen nur von der Größe eines Winkels abhängt. Die eindeutige Zuordnung zwischen Streckenverhältnissen und Winkeln lässt sich durch experimentelles Arbeiten mit einem DGS unterstützen.

Diese Erkenntnis soll im nächsten Schritt über Ähnlichkeiten oder Strahlensätze gesichert werden.

Begründung durch Ähnlichkeitsüberlegungen

Am Ende der Einführungssequenz steht dann die Definition der Begriffe Sinus, Kosinus und Tangens. Dafür sollten die einführenden Beispiele wieder aufgegriffen werden:
In Bezug auf das Anwendungsbeispiel "Der Kran" soll sich herausstellen, dass das Verhältnis zwischen der Hubhöhe und der Auslegerlänge allein vom Winkel α abhängt und dass es mit der Winkelfunktion Sinus bezeichnet wird: \[ \sin \alpha =\frac{Hubh\ddot{o}he}{Auslegerl\ddot{a}nge} \] Damit lässt sich also durch Wahl des Winkels und der Länge des Auslegers eine bestimmte Hubhöhe eindeutig einstellen. Das Anwendungsbeispiel "Straßensteigung" führt auf die Definition der Winkelfunktion Tangens: \[ \tan \alpha =\frac{H\ddot{o}hengewinn}{Luftlinie}\] Der Wert entspricht der Prozentangabe auf den Straßenschildern. Zu der Straße mit der steilsten Steigung von 35% gehört also ein Steigungswinkel von "nur" \( \alpha ={{\tan }^{-1}}(0,35)=19,29{}^\circ \).

Definition von Sinus, Kosinus und Tangens am rechtwinkligen Dreieck

1.3. Sinus, Kosinus und Tangens am Einheitskreis

Sinus, Kosinus und Tangens am Einheitskreis

Um Sinus, Kosinus und Tangens für beliebige Winkelgrößen einzuführen, wird meist vom Einheitskreis ausgegangen.

Einführungsbeispiel zu Sinus: Wasserrad

Das größte Wasserrad in Europa ist das "Great Laxey Wheel" mit 22m Durchmesser. Es wurde 1854 gebaut und diente bis 1929 dazu, Wasser aus einem Bergwerk zu pumpen. Die Achse des Rades schließt ungefähr mit dem oberen Ende der Gerinne ab, in die das Rad eingelassen ist. Die 168 Schaufeln sind in gleichen Abständen am Außenring des Rades befestigt. Es hat 24 Streben.

Mit diesem Beispiel können auch Vorkenntnisse der Lernenden zum Sinus am rechtwinkligen Dreieck aufgegriffen werden und der Begriff so erweitert werden. Zudem wird an diesem Beispiel die Einführung der Sinusfunktion vorbereitet.

Sinus, Kosinus und Tangens am Einheitskreis

Um den Tangens des Winkels zu bestimmen, betrachtet man die Strahlensatzfigur für z.B. α=45°. y(T) ist der Abstand des Punktes T von der x-Achse, es gilt \( \large \frac{1}{\cos \alpha }=\frac{y(T)}{\sin \alpha }\), also \(y(T)=\tan \alpha\).

1.4. Bestimmung einiger Funktionswerte und Zusammenhänge zwischen Sinus, Kosinus und Tangens

Bestimmung einiger Funktionswerte und Zusammenhänge zwischen Sinus, Kosinus und Tangens

Nach der Einführung von Sinus, Kosinus und Tangens (am rechtwinkligen Dreieck) sollten einige Funktionswerte exakt bestimmt und Zusammenhänge zwischen Sinus, Kosinus und Tangens herausgearbeitet werden. Das ist u. a. auch deshalb sinnvoll, da die Schülerinnen und Schüler hierbei immer wieder auf die Definitionen zurückgreifen müssen. Außerdem werden Unterrichtsinhalte früherer Jahre (z. B. Innenwinkelsatz, Satz des Pythagoras) wiederholt. Vor allem aber erfolgt eine Vernetzung geometrischer Überlegungen mit algebraischen Herleitungen.

Exakte Bestimmung einiger Funktionswerte

Erarbeiten Sie die Werte für den Sinus und den Kosinus der Winkelbeträge 30°, 45° und 60°.

Eine Hilfe erhalten Sie im Applet rechts.

Hilfe Funktionswerte

Zusammenhänge zwischen Sinus, Kosinus und Tangens

Zeigen Sie durch geometrische Überlegungen folgende Zusammenhänge:

\( \sin (90^\circ – \alpha) = \cos \alpha\) und \( \cos (90^\circ – \alpha) = \sin \alpha\)
\( \tan \alpha =\frac{\sin \alpha }{\cos \alpha }\)
Trigonometrischer Satz des Pythagoras für alle rechtwinkligen Dreiecke: \[ \sin^2 \alpha + cos^2 \alpha = 1\] (verkürzte Schreibweise \(\sin^2 α\) für \((\sin \alpha)^2 \))

Hilfe Zusammenhang