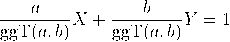3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.2. Lineare diophantische Gleichungen
___________________________________________________________________________
| Diophantische Gleichungen sind nach dem griechischen Mathematiker Diophantus (ca. 200 v.Chr. - 284 v. Chr.) benannt und spielen insbesondere in der algebraischen Zahlentheorie eine wichtige Rolle. Unter einer derartigen Gleichung versteht man eine polynomielle Gleichung mit ganzzahligen Koeffizienten bei der man sich insbesondere für die ganzzahligen Lösungen interessiert. Derartige Gleichungen haben häufig einen realen Bezug, so treten sie beispielsweise in der Chemie oder bei der Gewichteverteilung bei Balkenwaagen auf. |
|
Wir starten bescheiden mit einer linearen Gleichung in zwei Unbekannten  Gibt es also ganzzahlige Lösungen der obigen Gleichung? Angenommen, a und b sind nicht teilerfremd, also ggT(a,b) > 1, dann ist nach dem Korollar aus III.1. ax + by für beliebige ganzzahlige x,y stets ein Vielfaches von ggT(a,b) und also nie gleich eins; in diesem Fall ist die Gleichung also unlösbar. Sind jedoch a und b teilerfremd, also ggT(a,b) = 1 (gleich der rechten Seite), dann ist die Gleichung wiederum nach dem Korollar aus III.1. lösbar. Es ist gut zu wissen, wann diese Gleichung lösbar ist, aber im Falle ihrer Lösbarkeit ist es in der Praxis oft darüber hinaus sehr hilfreich, auch noch eine Lösung (oder gar alle) zu kennen. Unser bisheriges Argument reicht an dieser Stelle leider nicht aus, wohl aber hilft hier der euklidische Algorithmus aus dem vorhergehenden Kapitel weiter. Besonders gut lässt sich dies mit Hilfe eines Beispiels illustrieren. |
|
Aufgabe 1. Bestimmen Sie die Menge aller ganzzahligen Lösungen der linearen Gleichung  |
| Eine wichtige Verallgemeinerung unserer bisherigen Überlegungen (insbesondere des Korollars aus III.1.) liefert der |
|
Satz (Satz von Bézout). Die lineare Gleichung
mit ganzen Zahlen a,b,c ist genau dann ganzzahlig lösbar, wenn ggT(a,b) ein Teiler von c ist; in diesem Fall ist die Menge der ganzzahligen Lösungen gegeben durch
|
|
Beweis. Nach Obigem sind die Gleichungen (2) bzw. (3) ganzzahlig lösbar. Falls ggT(a,b) ein Teiler von c ist, d.h. c = dggT(a,b) für ein d ∈ ℤ, so ist mit einer Lösung x,y von (3) dann dx,dy eine Lösung der Gleichung:  Dank des euklidischen Algorithmus lässt sich die Lösungsgesamtheit wie folgt beschreiben: Gegeben eine spezielle ganzzahlige Lösung x0,y0 von (2), so ist insbesondere ggT(a,b) ein Teiler von c und jede Lösung von (1) ist – wie man sofort nachrechnet – von der Form
Der Satz ist somit vollständig bewiesen. qed. |
| Die ganzzahligen Lösungen einer linearen diophantischen Gleichung sind auch hinsichtlich der rationalen Approximation sehr interessant, siehe hierfür wiederum ein illustrierendes Beispiel. |