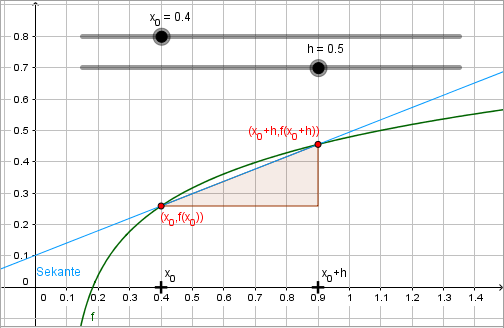
Geometrisch gedeutet, gibt er die Steigung der Sekanten durch die Punkte \( ( x_0\; \vert\; f(x_0) ) \) und \( ( x_0 + h \; \vert\; f(x_0 + h) ) \) an.
Demokurs: Didaktik der Analysis
Requisitos de finalización
1. Ableitung
1.1. Definition
Betrachtet wird eine in einem offenen Intervall \( J \) um \( x_0 \) definierte Funktion \( f \) mit
\[ f: \begin{cases} \mathbb{R} \supset J \to \mathbb{R},\\ x \to f(x) \end{cases} \]
Der Differenzenquotient
\[ \frac{ f(x_0 + h) - f(x_0)}{(x_0 + h)-x_0 } = \frac{ f(x_0 + h) - f(x_0)}{h} \]
mit \( x, x_0 \in J \subset \mathbb{R}, h \in \mathbb{R}, h > 0 \), beschreibt die (mittlere) Änderungsrate einer Funktion an der Stelle \( x_ 0\).
Falls der Grenzwert existiert, so gilt: Der Differenzialquotient
\[ \lim\limits_{h \to 0} \frac{ f(x_0 + h) - f(x_0)}{h} \] mit \( h \in \mathbb{R}, h > 0 \), beschreibt die lokale Änderungsrate einer Funktion im Punkt \(x_0\).
Geometrisch gedeutet gibt er die Steigung der Tangente im Punkt \( ( x_0 \; \vert\; f(x_0) ) \) an.
Existiert der Differenzialquotient, so heißt sein Wert Ableitung von \(f\) an der Stelle \(x_0\) und die Funktion \(f\) heißt differenzierbar in \(x_0\). Die Ableitung einer Funktion an einer Stelle \(x_0\) ist also eine Zahl, die aus einem Grenzprozess hervorgeht.
Das Bilden der Ableitung wird daher auch als Differenzieren, bzw. als Differentiation bezeichnet.
Die Ableitung einer Funktion lässt sich elementar berechnen, indem man den Differenzenquotienten bildet und den Grenzübergang durchführt. Hierdurch gewinnt man Ableitungsregeln für alle elementaren Funktionen.