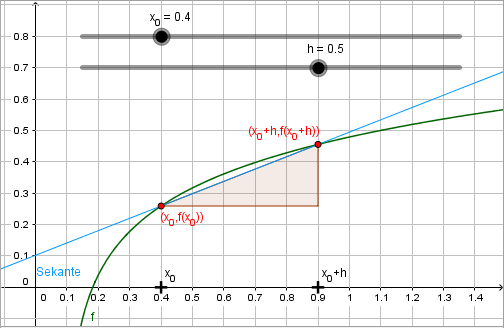
Geometrisch gedeutet, gibt er die Steigung der Sekanten durch die Punkte \( ( x_0\; \vert\; f(x_0) ) \) und \( ( x_0 + h \; \vert\; f(x_0 + h) ) \) an.
Demokurs: Didaktik der Analysis
| Website: | WueCampus |
| Kurs: | vhb - Demokurs Lehramt |
| Buch: | Demokurs: Didaktik der Analysis |
| Gedruckt von: | Gast |
| Datum: | Freitag, 22. November 2024, 00:21 |
1. Ableitung
Die Differenzialrechnung (oder Analysis) geht vor allem auf Sir Isaac Newton (1643–1727) und Gottfried Wilhelm Leibniz (1646–1716) zurück, wobei ihre heutige Form Ende des 19. Jahrhunderts entwickelt wurde. Sie stellt unter anderem eine wichtige Grundlage für zahlreiche Wissenschaften dar, wie etwa Physik, Elektrotechnik, Biologie oder die Wirtschaftswissenschaften. Im Hinblick auf ihren Einsatz in der Schule wird häufig kritisiert, dass im Unterricht zu viel Wert auf die Anwendung von Kalkülen gelegt werde, weshalb die Bildungsstandards für das Abitur (vgl. KMK 2012) verstärkt eine Orientierung an der Entwicklung des Begriffsverständnisses sowie an inhaltlichen und allgemeinen Kompetenzen fordern.
In diesem Kurs wird stets davon ausgegangen, dass die Differentiation vor der Integration (s. Kapitel 6) behandelt wird, wie dies heute in den meisten Schulbüchern üblich ist. Die historische Entwicklung der Differenzial- und Integralrechnung verlief allerdings anders (vgl. Volkert 1987).
Allgemeiner Hinweis
Durch Anklicken der Graphiken am rechten Rand der Buchseiten bzw. aller blau markierten Texte öffnen sich Pop-Ups, die Beispiele, Aufgaben oder Erläuterungen enthalten.
1.1. Definition
Betrachtet wird eine in einem offenen Intervall \( J \) um \( x_0 \) definierte Funktion \( f \) mit
\[ f: \begin{cases} \mathbb{R} \supset J \to \mathbb{R},\\ x \to f(x) \end{cases} \]
Der Differenzenquotient
\[ \frac{ f(x_0 + h) - f(x_0)}{(x_0 + h)-x_0 } = \frac{ f(x_0 + h) - f(x_0)}{h} \]
mit \( x, x_0 \in J \subset \mathbb{R}, h \in \mathbb{R}, h > 0 \), beschreibt die (mittlere) Änderungsrate einer Funktion an der Stelle \( x_ 0\).
Falls der Grenzwert existiert, so gilt: Der Differenzialquotient
\[ \lim\limits_{h \to 0} \frac{ f(x_0 + h) - f(x_0)}{h} \] mit \( h \in \mathbb{R}, h > 0 \), beschreibt die lokale Änderungsrate einer Funktion im Punkt \(x_0\).
Geometrisch gedeutet gibt er die Steigung der Tangente im Punkt \( ( x_0 \; \vert\; f(x_0) ) \) an.
Existiert der Differenzialquotient, so heißt sein Wert Ableitung von \(f\) an der Stelle \(x_0\) und die Funktion \(f\) heißt differenzierbar in \(x_0\). Die Ableitung einer Funktion an einer Stelle \(x_0\) ist also eine Zahl, die aus einem Grenzprozess hervorgeht.
Das Bilden der Ableitung wird daher auch als Differenzieren, bzw. als Differentiation bezeichnet.
Die Ableitung einer Funktion lässt sich elementar berechnen, indem man den Differenzenquotienten bildet und den Grenzübergang durchführt. Hierdurch gewinnt man Ableitungsregeln für alle elementaren Funktionen.
1.2. Grundvorstellungen zur Ableitung
Wie zuvor angedeutet, spielen vor allem zwei Aspekte beim Ableitungsbegriff eine Rolle:
- die Ableitung als Grenzwert des Differenzenquotienten und
- die Ableitung als lokale lineare Approximation
Mit diesen Aspekten wiederum sind jeweils verschiedene Grundvorstellungen verbunden:
1a) Lokale Änderungsrate
1b) Tangentensteigung
2a) Lokale Linearität
2b) Verstärkungsfaktor
1.3. Zugänge zum Ableitungsbegriff
Zugänge zum Ableitungsbegriff
Ein zentrales Ziel des Analysis-Unterrichts ist die Ausbildung von Grundvorstellungen, die der inhaltlichen Deutung mathematischer Begriffe dienen und deren Nutzen für Anwendungssituationen verdeutlichen.
Zu einer umfassenden Behandlung eines Begriffs und seiner Erfassung seiner Vernetzung mit anderen Begriffen der Analysis ist die Entwicklung verschiedener Vorstellungen notwendig.
Die Zugänge zum Ableitungsbegriff bauen jeweils primär auf einer der vorgestellten Grundvorstellungen auf (wobei stets Zusammenhänge zu den übrigen Vorstellungen bestehen).
Hier werden vor allem die zwei gängigsten unterrichtlichen Zugänge vorgestellt:
Zugang über lokale Änderungsraten
Dieser Zugang wird in den Bildungsstandards der KMK für das Abitur bevorzugt.
Hierbei wird auf die Beschreibung von Änderungs- oder Bewegungsprozessen zurückgegriffen, z.B. unter Betrachtung einer Funktion \(f \mapsto f(t)\), die jedem Zeitpunkt den zurückgelegten Weg zuordnet.
Die Frage nach der Momentangeschwindigkeit zu einem bestimmten Zeitpunkt \(t_0\) führt – aufbauend auf dem Geschwindigkeitsbegriff der Sekundarstufe I – zum Differenzenquotienten \(\left( \frac{\text{Weg}}{\text{Zeit}} \right) v = \frac{f(t) - f(t_0)}{t-t_0}, \; t\neq t_0\), der gerade der mittleren Änderungsrate, bzw. der physikalischen Durchschnittsgeschwindigkeit im Intervall \([t_0, t]\) entspricht.
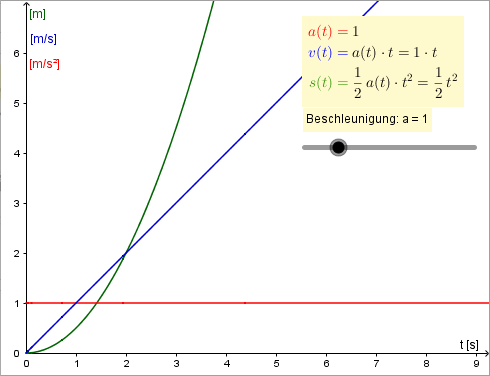
Exemplarisch lässt sich dieser Übergang anhand einer gleichmäßig beschleunigten Bewegung mit Beschleunigung \(a\) durchführen, deren zurückgelegte Strecke sich durch \(s(t) = \frac{1}{2}at^2\) beschreiben lässt.
Auch bei diesem Zugang lassen sich entsprechende Werte (in diesem Fall die Durchschnittsgeschwindigkeiten in immer kleiner werdenden Intervallen) mit einer Tabellenkalkulation aufzeigen; es kann beobachtet werden, dass sich diese Werte immer mehr dem einem bestimmten Wert annähern: der Momentangeschwindigkeit am Zeitpunkt \(t_0\), die der Ableitung von \(f\) entspricht.
Ermittlung der Durchschnittsgeschwindigkeit bei einer geradlinigen Bewegung mit der konstanten Beschleunigung \(a\)
Zugang über Sekanten und Tangenten
Aufbauend auf der vorgestellten Grundvorstellung wird bei diesem Zugang eine Tangente an den Graphen einer Funktion angelegt. Dazu werden ein fester Punkt \( P(x_0, f(x_0)) \) sowie ein beweglicher „Hilfspunkt“ \( Q(x_0+h, f(x_0 + h)), \; h\in\mathbb{R} \) gewählt. Durch \(P\) und \(Q\) wird eine Sekante gelegt und daraufhin schrittweise verkleinert. Diese Situation kann mit Hilfe dynamischer Geometrie-Programme von den Lernenden erkundet werden und die Idee der Tangenten als Grenzlage von Sekanten kann dadurch zuerst auf graphischer Ebene erfahren werden.
Oft wird in Graphiken nur \(h>0\) betrachtet. Doch auch der Fall \(h < 0\) sollte behandelt werden.
Der Fall \(h=0\), bei dem die Sekante „verschwindet“, kann im Unterricht durchaus thematisiert werden.
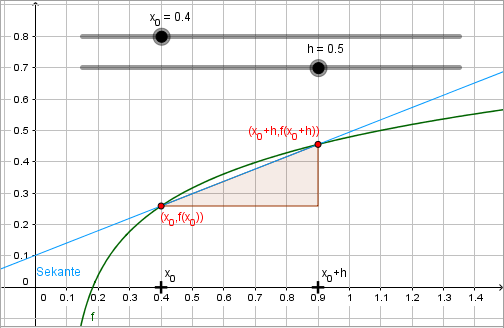
Die Sekantensteigung lässt sich (s. Definition) berechnen als \[ m_{PQ} = \frac{f(x_0 + h) - f(x_0)}{h}, \; h\neq 0 \]
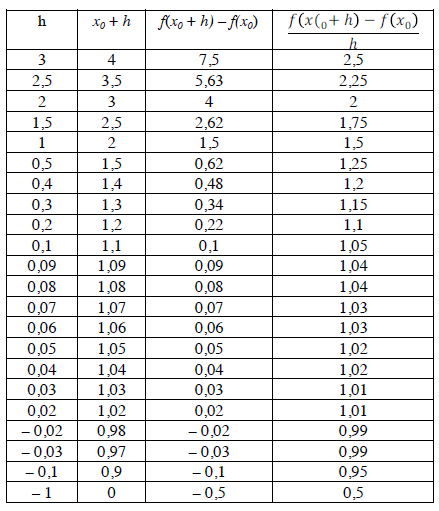
Der Grenzprozess \(h\to 0\) kann nun graphisch, numerisch und symbolisch veranschaulicht werden.
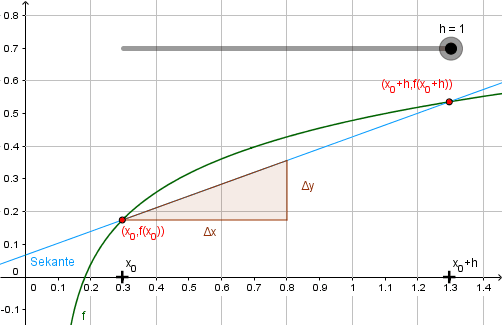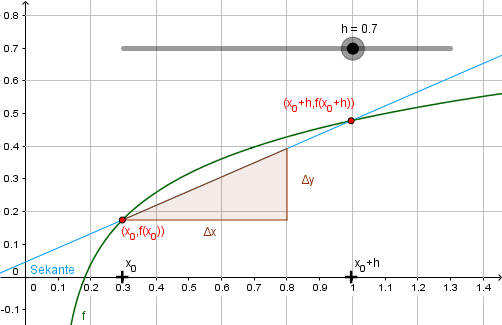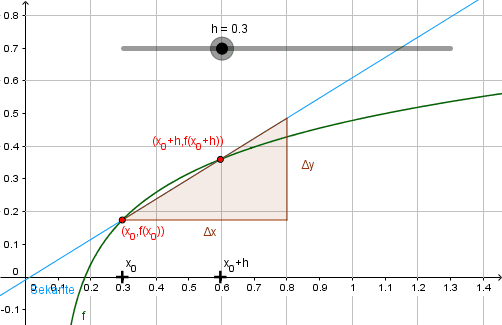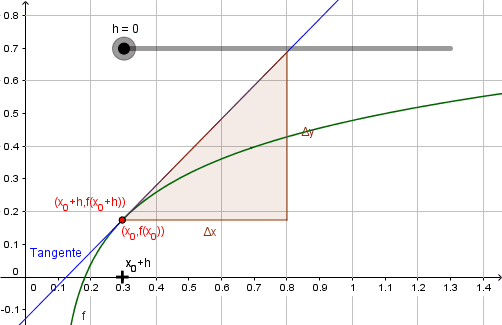
Die graphische Veranschaulichung lässt sich nur im Rahmen der Zeichengenauigkeit der verwendeten Software (oder einer klassischen Tafel) realisieren. Numerisch lässt sich der Grenzprozess ebenfalls nur diskret und bis zu einer gewissen Genauigkeit darstellen:
Tabellarische Darstellung des Annäherungsprozesses in \(x_0 = 1\) für \(f(x)=\frac{1}{2}x^2\)
Auf der symbolischen Ebene lässt sich die Ableitung entsprechend der Definition als Grenzwert des Differenzenquotienten für \(h\to 0\) herleiten – beispielsweise ebenfalls anhand der Funktion \(f(x)=\frac{1}{2}x^2\): \[ \begin{align*} \frac{f(x_0 + h) - f(x_0)}{h} &= \frac{\frac{1}{2}(x_0 + h)^2 - \frac{1}{2} {x_0}^2}{h} = \frac{\frac{1}{2} {x_0}^2 + x_0h + \frac{1}{2}h^2 - \frac{1}{2} {x_0}^2}{h} \\ &= x_0 + \frac{1}{2} h, \; h\neq 0 \end{align*}\]
Damit beträgt die Sekantensteigung für \(x_0 = 1\) gerade \(m=1 + \frac{1}{2}h\) und für den Grenzübergang \(h\to 0\) ergibt sich \(f'(x_0) = 1\).
1.4. Definition der Ableitung mittels Linearer Approximation
Diese Definition spielt im Unterricht eine eher untergeordnete Rolle und wird hier nur ergänzend vorgestellt.
\(f\) sei eine in einer offenen Umgebung von \(x_0\in\mathbb{R}\) definierte reellwertige Funktion.
\(f\) heißt differenzierbar an der Stelle \(x_0\), wenn eine Zahl existiert, sodass gilt:
\[ f(x) = f(x_0) + m\cdot (x-x_0) + r(x-x_0),\]
wobei für die Restfunktion \(r\) gilt:
\[ \lim\limits_{x \to x_0} \frac{ r(x-x_0)}{x-x_0} = 0 \]
\(m\) wird dann Ableitung von \(f\) an der Stelle \(x_0\) genannt; \(f'(x_0)=:m\).
Zur Vermeidung des Quotienten im Grenzwert lässt sich stattdessen auch definieren:
\[ f(x) = f(x_0) + m\cdot (x-x_0) + (x-x_0) \cdot R(x-x_0), \]
wobei
\[ \lim\limits_{x \to x_0} R(x-x_0) = 0 \]
Bedeutung der Definition:
Für lineare Funktionen lässt sich jeder Funktionswert \(f(x)\) aus dem Funktionswert an einer festen Stelle \(x_0\) berechnen, indem die Differenz \(x-x_0\) mit der Steigung \(m\in\mathbb{R}\) multipliziert wird:
\[f(x)=f(x_0) + (x-x_0)\cdot m.\]
Bei nichtlinearen Funktionen muss die Steigung in Abhängigkeit von der Stelle modifiziert werden, doch lokal passt die Approximation gut, sofern die Modifikation \(R(x-x_0)\) lokal klein ist und im Grenzwert verschwindet, d.h.:
\[ f(x) = f(x_0) + (x-x_0) \cdot (m + R(x-x_0)) \text{ mit } \lim\limits_{x \to x_0} R(x-x_0) = 0.\]
1.5. Graphisches Differenzieren
Graphisch differenzieren
Vom Verständnis der Ableitung als Tangentensteigung ausgehend kann ohne formale Berechnungs-Verfahren graphisch differenziert werden. Dazu muss an einzelnen Punkten des Graphen einer Funktion die Steigung ermittelt werden (z.B. durch Anlegen einer Tangente). Der (gemessene) Wert für deren Steigung wird als Ordinate (y-Wert) – gemeinsam mit der zugehörigen Abszisse (x-Wert) – als Punkt in ein (zweites) Koordinatensystem übertragen.
Dynamische Geometrie-Software ermöglicht, die Stelle, an der die Tangente gebildet wird, zu verschieben und die entsprechenden Punkte im zweiten Koordinatensystem durch die Spurfunktion der Software anzeigen zu lassen. So gelangt man „punktuell“ zum Graphen der zugehörigen Ableitungsfunktion.
1.6. Lernen in Stufen - Ableitung
Das Stufenschema des Begriffsverständnisses nach Vollrath
1. Stufe: Der Begriff als Phänomen
Auf dieser Stufe erwerben Lernende ein intuitives Begriffsverständnis. Ihnen sind Begriffe wie Durchschnitt, durchschnittliche und mittlere Änderungsrate, Steigung (von Geraden) sowie Steigen und Fallen von Graphen bekannt und sie können diese anhand von Beispielen aufzeigen und erklären.
2. Stufe: Der Begriff als Träger von Eigenschaften
Auf dieser Stufe erwerben Lernende ein inhaltliches Begriffsverständnis. Ihnen der Begriff der absoluten Änderung bekannt. Sie haben Einsicht in den Grenzwertprozess beim Übergang von Differenzen- zu Differentialquotient und können diesen anhand von Sekanten(steigungen) und Tangenten(steigungen) geometrisch deuten. Ihnen ist bewusst, dass die Ableitungsfunktion ihrerseits ebenfalls abgeleitet werden kann, was zum Begriff der höheren Ableitungen führt. Des Weiteren beherrschen sie die grundlegenden Ableitungsregeln.
3. Stufe: Der Begriff als Teil eines Begriffsnetzes
Auf dieser Stufe erwerben Lernende ein integriertes Begriffsverständnis. Ihnen sind Beziehungen zwischen den Eigenschaften einer Funktion und denen ihrer Ableitungen bewusst; So sind ihnen bspw. Beziehungen zwischen der Ableitung einer Funktion und dem Monotonieverhalten ihres Graphen bewusst und sie können dieses Wissen zur Berechnung von Extremwerten nutzen. Sie können diese Methodik im Folgenden auf die Berechnung von Wendepunkten übertragen. Weiterhin können sie zwischen lokaler und globaler Differenzierbarkeit unterscheiden.
Sie können den Ableitungsbegriff zu außermathematischen Situationen in Beziehung setzen.
4. Stufe: Der Begriff als Objekt zum Operieren
Auf dieser Stufe erwerben Lernende ein formales Begriffsverständnis. Sie können formal korrekte Definitionen wiedergeben und diese zum Führen von Beweisen nutzen. Sie beherrschen die Berechnung der Ableitung – auch bei Exponential-, Logarithmus- und trigonometrischen Funktionen. Sie verfügen über eine globale Sichtweise auf den Ableitungsbegriff und die Ableitungsfunktion und ihren Graphen als eigenständige Objekte, mit denen sie operieren.
5. Stufe: „kritisch“
Auf dieser Stufe erwerben Lernende ein kritisches Begriffsverständnis. Sie können den hinter dem Ableitungsbegriff stehenden Konstruktionsprozess beschreiben und erklären. Sie können über damit verbundene Schwierigkeiten reflektieren und ihr Wissen zur Verbesserung des eigenen Lernprozesses nutzen.
1.7. Aufgaben
Aufgabe 1
- Differenzieren Sie den Term für das Volumen einer Kugel nach dem Radius \(r\). Interpretieren Sie das Ergebnis geometrisch und erklären Sie dies mithilfe verschiedener Grundvorstellungen.
- Wiederholen Sie das für das Volumen eines Würfels.
- Betrachten Sie auch die Ableitung des Terms für das Volumen eines Kegels konstanter Höhe in Abhängigkeit vom Radius des Grundkreises. Inwiefern ist dieser Fall anders als die vorhergehe
Aufgabe 2
- Begründen Sie mit möglichst vielen verschiedenen Grundvorstellungen, dass an der Stelle eines lokalen Extremums die Ableitung 0 ist.
- Ein Schüler sagt, die Wurzelfunktion \(f:x\to \sqrt{x}\) habe in \(x=0\) ein globales Minimum. Eine Mitschülerin entgegnet, die erste Ableitung sei dort aber nicht 0. Klären Sie die Lage!
Aufgabe 3
- Begründen Sie, warum die Betragsfunktion an der Stelle 0 nicht differenzierbar ist.
- Untersuchen Sie die symmetrische Ableitung \[\lim_{n \to 0} \frac{f(x+h) - f(x-h)}{2h}\] für die Funktionen mit den Termen \(x^2\), \(x^3\) , \(|x|\).
- Nennen Sie Vor- und Nachteile der symmetrischen Ableitung.
Aufgabe 4
- Erläutern Sie im Zusammenhang mit quadratischen Funktionen die Begriffe
- allgemeine Form der Funktionsgleichung,
- Scheitelpunktform und
- Quadratische Ergänzung
- Erläutern Sie, wie mit Hilfe der quadratischen Ergänzung ein Extremwertproblem ohne Verwendung der Ableitung gelöst werden kann.
- Führen Sie dieses Verfahren an einem für den Analysisunterricht geeigneten Beispiel durch.
- Erläutern Sie Vor- und Nachteile.