3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik
vhb - Kurs: Grundlagen der elementaren Zahlentheorie
III.3.1 Approximationssatz von Dirichlet
_______________________________________________________________
| Die Menge ℚ liegt dicht in der Menge ℝ, d.h. in jeder noch so kleinen Umgebung einer beliebigen reellen Zahl gibt es eine (tatsächlich sogar unendlich viele) rationale Zahl(en). Insofern macht es Sinn, reelle Zahlen durch rationale approximieren zu wollen, aber wie macht man das? |
| Eine wichtige Frage ist dabei, wann eine rationale Zahl überhaupt eine gute rationale Approximation genannt werden sollte? Eine mögliche Antwort hierauf liefert der folgende |
| Satz (Approximationssatz von Dirichlet, 1842). Zu einer Irrationalzahl α gibt es unendlich viele rationale Zahlen p/q mit |
|
Beweis. Wir notieren den Ganzteil und den gebrochenen Anteil einer reellen Zahl x als 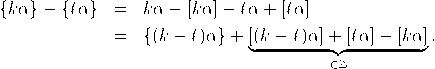 Weil nun {kα}−{ℓα} in dem Intervall [0,1/Q) liegt, addieren sich die Ganzteile in der vorangegangenen Formel zu null auf. Sei nun q = k − ℓ, dann gilt also {qα} = {kα}−{ℓα} <1/Q. Mit p := [qα] folgt ferner welches wegen q < Q die gewünschte Abschätzung liefert. Jetzt nehmen wir an, dass α irrational ist und nur endlich viele p1/q1,…,pn/qn der gewünschten Ungleichung genügen. Mit der Irrationalität von α gibt es dann ein Q mit |α −pj/qj| >1/Q für j = 1,…,n, was der oberen Abschätzung gegen 1/(qjQ) widerspricht. Damit ist der Satz bewiesen. qed. |
|
Der Beweis des Dirichletschen Approximationssatzes zeigt leider nicht, wie zu einer gegebenen Irrationalzahl wirklich gute rationale Approximationen tatsächlich gefunden werden können. Tatsächlich charakterisiert die Approximationseigenschaft des Dirichletschen Approximationssatzes Irrationalzahlen: |
Satz. Für rationale Zahlen α gibt es nur endlich viele rationale Zahlen p/q mit
![]()
| Die Frage, ob eine gegebene reelle Zahl α irrational ist, lässt sich also durch die Qualität rationaler Näherungen beantworten. Im Falle eines irrationalen α existieren unendlich viele p/q, die um weniger als 1/q2 von α abweichen, während für rationale α nur endlich viele solche existieren. |
| Beweis. Ist α = m/n mit teilerfremden m,n und m/n ≠ p/q, so gilt |
