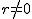Kegelschnitte
Abschlussbedingungen
7. Kegelschnitte
| Satz 7.2 Fünfpunktesatz Durch fünf Punkte einer Ebene, von denen keine vier kollinear sind, gibt es immer einen Kegelschnitt. Ferner existiert zu gegebenen paarweise verschiedenen fünf Punkten einer Ebene, von denen keine drei auf einer Geraden liegen, ein eindeutiger Kegelschnitt durch diese fünf Punkte. |
| Dieser Idee liegt auch das Global Positioning System (GPS) zugrunde, welches die Navigation (etwa mit Autos) erleichtert. |