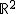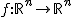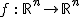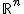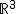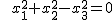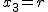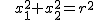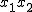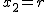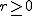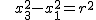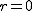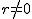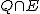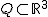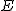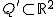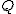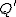|
Ein Kreiskegel im euklidischen Raum 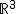 lässt sich durch die quadratische Gleichung lässt sich durch die quadratische Gleichung
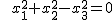
beschreiben. Schneiden wir diesen Kreiskegel etwa mit der Ebene, die durch 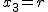 mit einer fixierten positiven reellen Zahl mit einer fixierten positiven reellen Zahl  definiert ist, so ergibt sich durch Einsetzen in der Kreiskegelgleichung die Gleichung definiert ist, so ergibt sich durch Einsetzen in der Kreiskegelgleichung die Gleichung
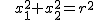 . .
Diese beschreibt bekanntlich einen Kreis vom Radius  mit Mittelpunkt im Ursprung in der mit Mittelpunkt im Ursprung in der 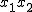 -Ebene. Also ist die Schnittkurve unseres Kegels mit besagter Ebene eben dieser Kreis. Wählen wir statt -Ebene. Also ist die Schnittkurve unseres Kegels mit besagter Ebene eben dieser Kreis. Wählen wir statt 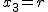 eine etwas geneigte Ebene, so ergeben sich Ellipse bzw. Parabel als Schnittkurven, wobei die Parabel genau dann entsteht, wenn die Winkel bei Ebene und Kegel übereinstimmen (siehe nachstehende Abbildungen). eine etwas geneigte Ebene, so ergeben sich Ellipse bzw. Parabel als Schnittkurven, wobei die Parabel genau dann entsteht, wenn die Winkel bei Ebene und Kegel übereinstimmen (siehe nachstehende Abbildungen).
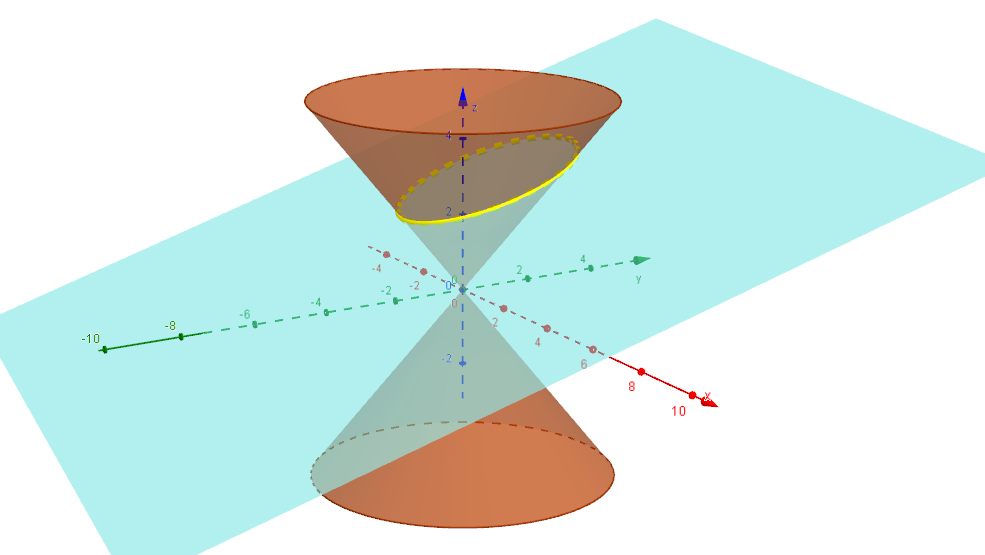
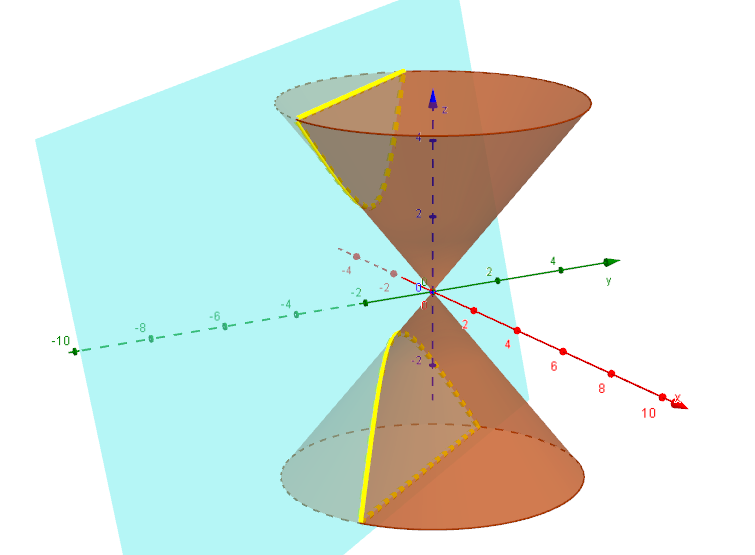
Schneiden wir hingegen mit einer Ebene 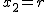 , wobei , wobei 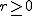 sei, so folgt nach Umstellen die Gleichung sei, so folgt nach Umstellen die Gleichung
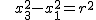 ; ;
damit ist die Schnittkurve in diesem Fall ein Geradenpaar (wenn 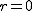 ) oder eine Hyperbel (wenn ) oder eine Hyperbel (wenn 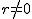 ; siehe nachstehende Abbildung). ; siehe nachstehende Abbildung).
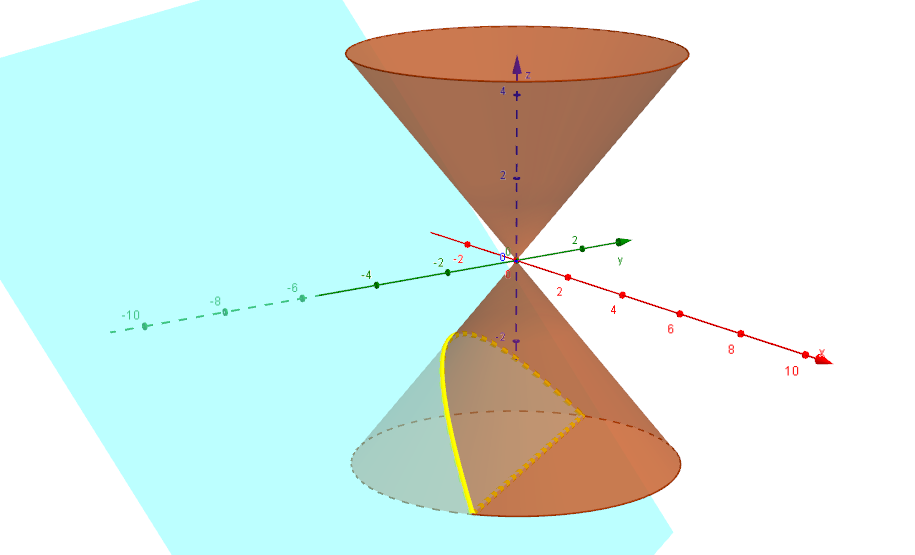
Folgender zentraler Satz besagt, dass wir sämtliche Quadriken der Ebene (bis auf Ähnlichkeit) als Schnitte von Ebenen mit einem Kreiskegel im dreidimensionalen Raum realisieren können. Aus diesem Grund nennt man die Quadriken der Ebene auch Kegelschnitte.
|