Demokurs: Grundlagen der anwendungsbezogenen Hochschulmathematik
1. Funktionen
1.1. Lineare und quadratische Funktionen


Funktionen und Stetigkeit - Lineare und quadratische Funktionen
In diesem Kapitel wird der Funktionsbegriff definiert und erläutert. Im Anschluss daran werden verschiedene bereits aus der Schule bekannte Funktionen eingehend betrachtet.
Was ist eine Funktion?
Beispiel 1:
Zwischen der in Metern pro Sekunde gemessenen Schallgeschwindigkeit \(c\) und der in Grad Celsius gemessenen Lufttemperatur \(\theta\) besteht der Zusammenhang
\(c = 331,5 \cdot \sqrt{1 + \frac{\theta}{273} }\, \text{für } \, \theta > - 273\)
\(c = c(\theta)\) ist eine Funktion von \(\theta\).

Definition 1 (Funktion)
Zu beliebigen Mengen \(A\) und \(B\) versteht man unter einer Funktion (bzw. Abbildung) \(f : A \rightarrow B\) eine Vorschrift, die jedem(!) \(x \in A\) genau einen Funktionswert \(y = f(x) \in B\) zuordnet. \(A\) heißt dabei Definitions- und \(B\) Wertebereich. Der Graph von \(f\) ist die Menge \(G_f= \{(x,y) \in A × B : y = f(x)\}\)
Erklärung: Eine Funktion ist also eine eindeutige Zuordnungs-Vorschrift
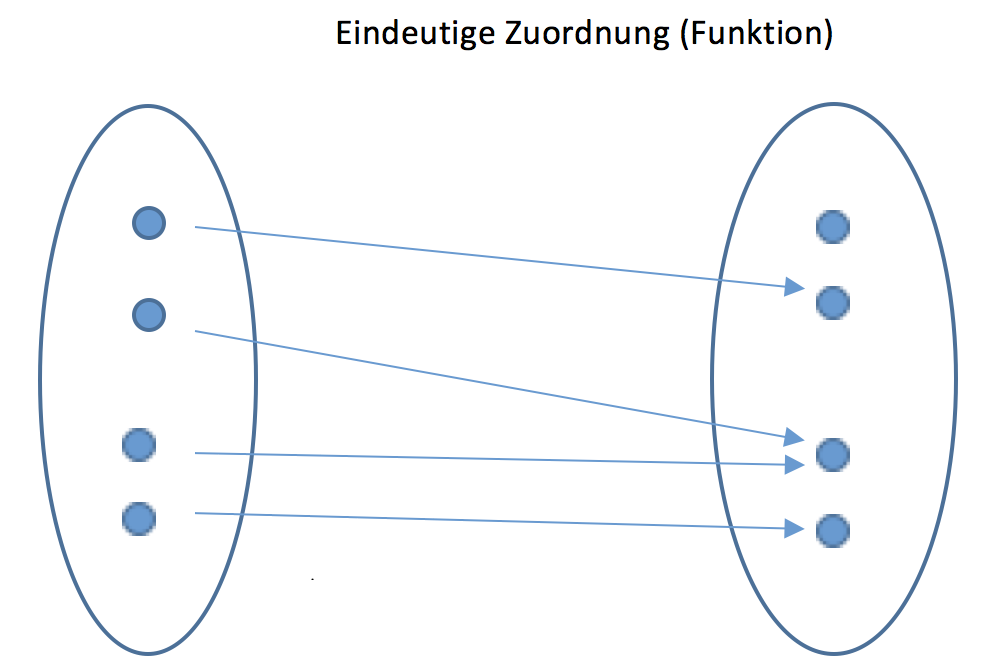
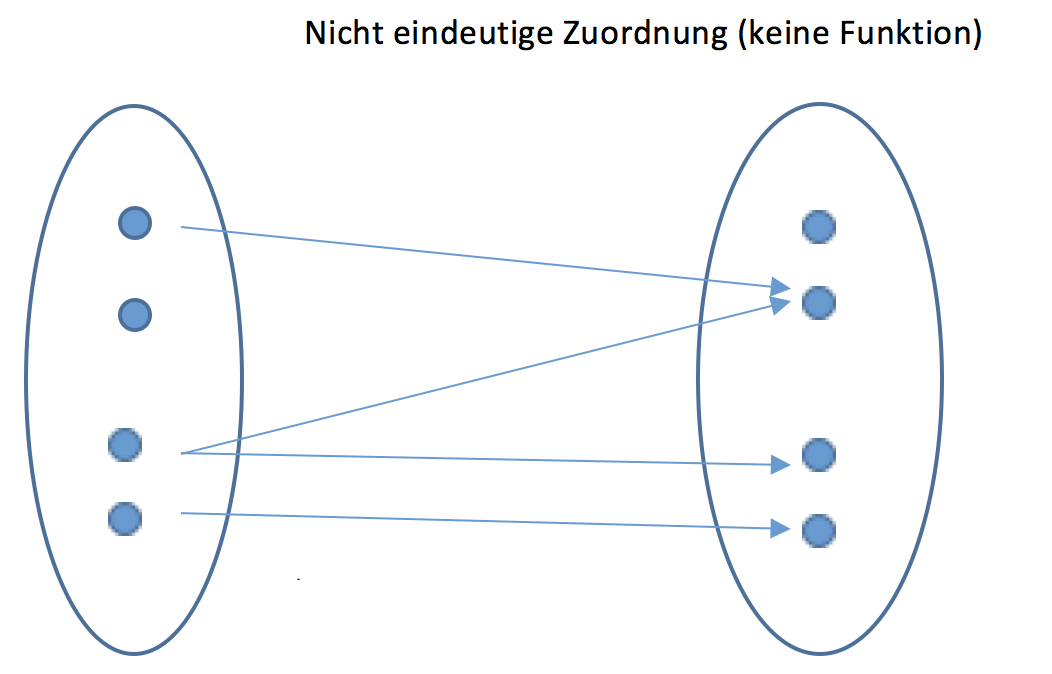
In diesem Beispiel wird jeder natürlichen Zahl \(x\) ihr Quadrat \(y = f(x) = { x }^{ 2 }\) zugeordnet.
Für gewöhnlich werden die hier relevanten Funktionen als Graph in einem Koordinatensystem dargestellt. Beim Graphen handelt es sich, wie oben definiert, um eine Punktemenge, die die bekannte Kurven-Darstellung ergibt. Die Punkte haben die Form \((x|f(x))\) .

Lineare Funktionen
Die Funktionsgleichung einer linearen Funktion \(f : x \in \mathbb{R} \rightarrow f(x) \in \mathbb{R}\) lautet:
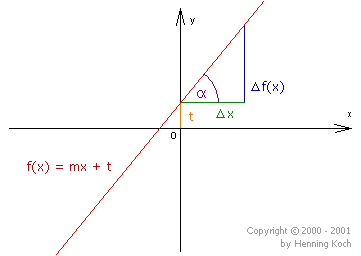
\(f(x) = m \cdot x + t \, \) mit \(\, m, \, t \in \mathbb{R}\)
\(m\) wird dabei als Steigung und \(t\) als y-Achsenabschnitt der Funktion (genauer: des Graphen der Funktion) bezeichnet.
Die Graphen linearer Funktionen sind Geraden. Bei positiver Steigung \(m > 0\) „steigt“ die Gerade, bei negativer Steigung \(m < 0\) „fällt“ die Gerade.
Diese Schreibweise bedeutet, dass die Funktionsvorschrift \(f\) einem Wert \(x\) (dem „Urbild“) einen Funktionswert \(f(x)\) (das „Bild“) zuordnet. Sowohl \(x\) als auch \(f(x)\) liegen in diesem Fall in \(\mathbb{R}\).
Je größer der Betrag von \(m\) gewählt wird, desto steiler verläuft die Gerade: Je größer eine positive Steigung ist, desto steiler verläuft sie aufwärts; je kleiner eine negative Steigung, desto steiler verläuft sie abwärts. Analog dazu wird die Gerade für kleinere positive \(m\), bzw. für größere negative \(m\) flacher.
Für \(m=0\) ergibt sich der Sonderfall einer Gerade, die parallel zur \(x\)-Achse, also waagrecht, verläuft:
\(f(x) = t\)
Der Betrag \(|a|\) einer Zahl \(a\) ist deren „Absolutwert“, also ihr Wert „ohne Vorzeichen“: \(|3|=3\) \(|-3|=3\)
Entsprechend kann die Betragsfunktion
\(f(x)=|x|=\begin{cases} x, \text{für } x\geq 0\\ -x, \text{für } x < 0\end{cases}\)
definiert werden:
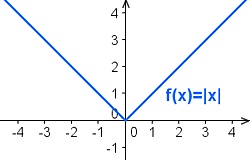
Man sollte jedoch beachten, dass mit der linearen Funktion keine Geraden dargestellt werden können, die parallel zur y-Achse verlaufen (was der Definition einer Funktion widersprechen würde), da hierzu die Steigung unendlich groß sein müsste und einem einzigen \(x\)-Wert mehrere (unendlich viele) Werte zugeordnet würden.
Derartige Geraden können hingegen mit der folgenden Gleichung (nicht Funktionsgleichung!) dargestellt werden:
\(x=a, a\in \mathbb{R}\)
Da \(t\) unabhängig von \(x\) (\(t\) verändert sich also nicht für verschiedene \(x\)-Werte/ ist für alle \(x\) gleich.) den Funktionswert erhöht oder erniedrigt, kann man durch \(t\) den gesamten Graphen an der \(y\)-Achse entlang verschieben. Für positives \(t\) wird der Graph nach oben und für negatives \(t\) nach unten verschoben. Ist \(t=0\), so verläuft die Gerade durch den Ursprung; es gilt nämlich
\(f(0)=m\cdot 0+t=t=0\).
Man spricht entsprechend von einer Ursprungsgerade.
Untersuchen Sie den Einfluss der Parameter \(m\) und \(t\) auf die lineare Funktion!

Berechnung der Steigung und des y-Achsenabschnitts
Die Steigung einer linearen Funktion berechnet sich mit Hilfe des Steigungsdreiecks wie folgt:
\(m = \frac{\Delta y}{\Delta x} = \frac{\Delta f(x)}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} \)
Dabei wird der vertikale Abstand zweier Punkte des Graphen durch den horizontalen Abstand der beiden Punkte geteilt (genauer gesagt, die Werte der jeweiligen Abstände). Die Steigung gibt also an, um welchen Wert sich die Funktion vertikal ändert, wenn horizontal eine gewisse Änderung erfolgt.
Ähnlich wird bspw. bei Steigungen im Straßenverkehr verfahren. Es wird gemessen, um wie viele Höhenmeter sich ein Fahrzeug nach oben bewegt, während es sich 100m in der Waagrechten fortbewegt. (Die tatsächlich zurückgelegte Strecke stellt dann die Hypotenuse des entstehenden rechtwinkligen Dreiecks dar.) Auf Grund dieser Idee – \(x\) Höhenmeter pro 100m in der Ebene – wird die entsprechende Steigung in Prozent („pro Hundert“) angegeben.

Der y-Achsenabschnitt \(t\) ist der Wert der Funktion bei \(x=0\), der sich berechnen lässt, indem \(0\) in die Funktionsvorschrift eingesetzt wird:
\(t = f(0)\)
Zeichnen des Funktionsgraphen
Zum Zeichnen des Funktionsgraphen sollte man sich folgende Vorgehensweise einprägen:
- Vom Ursprung aus um \(t\) an der \(y\)-Achse „entlanggehen“. Wir nennen diesen Punkt \(P\).
- Von \(P\) aus um den Wert des Zählers von \(m\) (s. Steigungsdreieck) nach oben und um den Wert des Nenners von \(m\) nach rechts gehen. Wir nennen diesen Punkt \(Q\).
- Der Graph ist eine Gerade durch \(P\) und \(Q\).
Ist \(m\) bereits berechnet worden, so lässt sich als Zähler in obiger Vorgehensweise \(m\) verwenden, als Nenner 1, denn es gilt: \(m = \frac{m}{1}\)
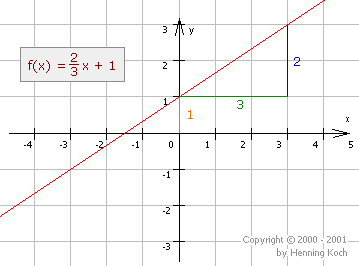
Berechnung des Winkels zwischen Gerade und x-Achse
Wir betrachten das rechtwinkelige Steigungsdreieck. Mit Hilfe der Definition für die Winkelfunktion Tangens im rechtwinkligen Dreieck ((Länge der) „Gegenkathete geteilt durch (Länge der) Ankathete“) gilt:
\(tan(\alpha ) = \frac{\Delta f(x)}{\Delta x} = m\)
nach Definition der Steigung \(m\) und damit
\( \alpha = arctan(m)\)

Nullstellen
Eine lineare Funktion hat genau eine Nullstelle ( \(f(x)=0\) ), also genau einen Schnittpunkt mit der \(x\)-Achse.
Ausgenommen ist der Sonderfall \(m=0\). Damit wäre \(f\) eine konstante Funktion und ihr Graph eine Parallele zur \(x\)-Achse: \(f(x)=t\). Eine solche Funktion hat keine Nullstellen für \(t \neq 0\). Für \(t = 0\) gilt: \(f(x)=0\). In diesem Fall hat die Funktion ausschließlich (und damit unendlich viele) Nullstellen.
Zur Berechnung der Nullstelle \(x_0\) setzt man \(f(x_0)=m\cdot x_0+t = 0\) und löst diese Gleichung nach \(x_0\) auf:
\(x_0 = - \frac{t}{m}\)
Beziehungen zwischen den Graphen einer linearen Funktion
Zwei Geraden sind genau dann parallel, wenn ihre Steigung gleich ist:
\(m_1 = m_2 \Leftrightarrow G_f \parallel G_g\)
Parallele Geraden \(f_1, f_2, f_3,\ldots \) unterscheiden sich also nur durch ihre \(y\)-Achsenabschnitte \(t_1, t_2, t_3,\ldots \) Sie gehen also durch Parallel-Verschiebungen in vertikaler Richtung (nach oben und nach unten) auseinander hervor.
Zwei Geraden \(f=m_1x+t_1\) und \(g=m_2x+t_2\) stehen genau dann aufeinander senkrecht, wenn das Produkt der beiden Steigungen \(-1\) ergibt:
\(m_1 \cdot m_2 = - 1 \Leftrightarrow G_f \bot G_g\)
\(G_f\) bezeichnet den Funktionsgraphen der Funktion \(f\).

Aufgabe:
Begründen Sie diesen Zusammenhang zwischen \(m_1\) und \(m_2\).

Quadratische Funktionen
Die allgemeine Form der quadratischen Funktion \(f : x \rightarrow f(x)\) lautet:
\(f(x) = a \cdot x^2 + b \cdot x + c \, \) mit \( \, a, \,b, \,c \in \mathbb{R}\)
Die Graphen quadratischer Funktionen sind Parabeln. Der Koeffizient („Vorfaktor“) von \(x^2\), also \(a\), bestimmt die Form der Parabel. Bei einem positivem Wert von \(a\) ist die Parabel nach oben, bei einem negativen Wert nach unten geöffnet. Je größer \(|a|\) gewählt wird, desto "enger" wird die Parabel. Analog wird die Form der Parabel für kleineres \(|a|\) weiter. Eine Veränderung des Parameter \(c\) bewirkt eine Verschiebung der Parabel in y-Richtung, denn \(c\) ist unabhängig von \(x\). Veränderungen in \(x\) bewirken also keine Veränderungen in \(c\).
Wird \(c\) um eins erhöht, dann wird der Graph um eine Einheit nach oben verschoben. Wird \(c\) um eins verringert, wird der Graph dagegen um eine Einheit nach unten verschoben.
\(c\) entspricht also sozusagen dem \(y\)-Achsenabschnitt, den wir von den Geraden kennen.
\(|a|\) bezeichnet den Betrag, bzw. Absolutwert von \(a\), also den Wert von \(a\) „ohne negatives Vorzeichen“
\(f(x)=|x|=\begin{cases} x, \text{für } x\geq 0\\ -x, \text{für } x < 0\end{cases}\)
Scheitelpunktsbestimmung
Der Scheitelpunkt der Parabel ist entweder das absolute Minimum (falls \(a\) positiv ist) oder das absolute Maximum (wenn \(a\) negativ ist). Die Koordinaten des Scheitelpunkts lassen sich direkt ablesen, wenn der Funktionsterm mittels quadratischer Ergänzung unter Ausnutzung der binomischen Formeln in die Scheitelpunktsform umgeformt wird:
\(f(x) = a \cdot (x - x_S)^2 + y_S\)
Bei dieser Form der Funktionsgleichung lässt sich der graph von \(f\) als Variation der Normalparabel mit Gleichung \(g(x) = x^2\) interpretieren.
\(f\) entsteht aus dieser durch Verschiebung um \(x_s\) nach rechts, um \(y_s\) nach oben und durch Streckung/Stauchung um den Faktor \(a\).
Als „absolut“ (oder „global“) wird ein Extremum (Maximum oder Minimum) bezeichnet, wenn es sich dabei um den größten/ kleinsten Wert im gesamten Definitionsbereich handelt. Im Gegensatz dazu ist ein „lokales“ Maximum/ Minimum nur Maximum/ Minimum in einer bestimmten Umgebung.
Der Koeffizient \(a\) ändert sich bei der Umformung nicht!
Mit den Koeffizienten der allgemeinen Form für quadratische Gleichungen (s. oben) ergeben sich die Koordinaten des Scheitelpunkts dann zu:
\(x_s = -\frac{b}{2a}\)
\(y_s = -\frac{4ac - b^2}{4a}\)
Der Scheitelpunkt hat dann die koordinaten \(S(x_s|y_s)\). Der Graph von \(f\) ist achsensymmetrisch zu einer Parallelen zur \(y\)-Achse durch \(x_s\).

Zeigen Sie, wie die allgemeine Form \(f(x) = ax^2+ bx + c \,\) in die Scheitelpunktform \(f(x) = a \cdot (x - x_S)^2+ y_S\) überführt werden kann.
Eine quadratische Funktion hat je nach Lage des Scheitelpunktes \(S\) und dem Vorzeichen von \(a\) keine, eine oder zwei Nullstellen.
Zur Berechnung der Nullstellen setzt man \(f(x) = 0\) und löst die Gleichung mittels der quadratischen Lösungsformel:
\(x_{1,2} = \frac{1}{2a} (-b \pm \sqrt{b^2 - 4ac})\)

Aufgabe 1:
Berechnen Sie die Nullstellen der Funktion \(f\) und zeichnen Sie den Funktionsgraphen für \(f(x) = -3x + 6\).
Aufgabe 2:
Gegeben sind zwei Punkte \(P = (4|3)\) und \(Q = (0|-2)\). Bilden Sie die Gleichung der Geraden \(g\) durch \(P\) und \(Q\) und berechnen Sie den Winkel, den \(g\) mit der x-Achse einschließt!
Aufgabe 3:
Bestimmen Sie durch quadratische Ergänzung den Scheitelpunkt \(S\) der Parabel mit \(f(x) = -5x^2+ 30x + 47\).
Aufgabe 4:
Berechnen Sie die Nullstellen folgender Parabel mit \(f(x) = -\frac{1}{2} x^2 + \frac{1}{2} x + 3\).

