Demokurs: Grundlagen der anwendungsbezogenen Hochschulmathematik
| Startsida: | WueCampus |
| Kurs: | vhb - Demokurs Lehramt |
| Bok: | Demokurs: Grundlagen der anwendungsbezogenen Hochschulmathematik |
| Utskrivet av: | مستخدم ضيف |
| Datum: | måndag, 8 december 2025, 21:07 |
1. Funktionen


Das Kapitel Funktionen umfasst:

- Funktionen - Lineare und quadratische Funktionen
- Potenzfunktionen, Polynome und Potenzreihen
- Exponentialfunktion und Wachstum
- Trigonometrische Funktionen
- Aufgaben

1.1. Lineare und quadratische Funktionen


Funktionen und Stetigkeit - Lineare und quadratische Funktionen
In diesem Kapitel wird der Funktionsbegriff definiert und erläutert. Im Anschluss daran werden verschiedene bereits aus der Schule bekannte Funktionen eingehend betrachtet.
Was ist eine Funktion?
Beispiel 1:
Zwischen der in Metern pro Sekunde gemessenen Schallgeschwindigkeit \(c\) und der in Grad Celsius gemessenen Lufttemperatur \(\theta\) besteht der Zusammenhang
\(c = 331,5 \cdot \sqrt{1 + \frac{\theta}{273} }\, \text{für } \, \theta > - 273\)
\(c = c(\theta)\) ist eine Funktion von \(\theta\).

Definition 1 (Funktion)
Zu beliebigen Mengen \(A\) und \(B\) versteht man unter einer Funktion (bzw. Abbildung) \(f : A \rightarrow B\) eine Vorschrift, die jedem(!) \(x \in A\) genau einen Funktionswert \(y = f(x) \in B\) zuordnet. \(A\) heißt dabei Definitions- und \(B\) Wertebereich. Der Graph von \(f\) ist die Menge \(G_f= \{(x,y) \in A × B : y = f(x)\}\)
Erklärung: Eine Funktion ist also eine eindeutige Zuordnungs-Vorschrift
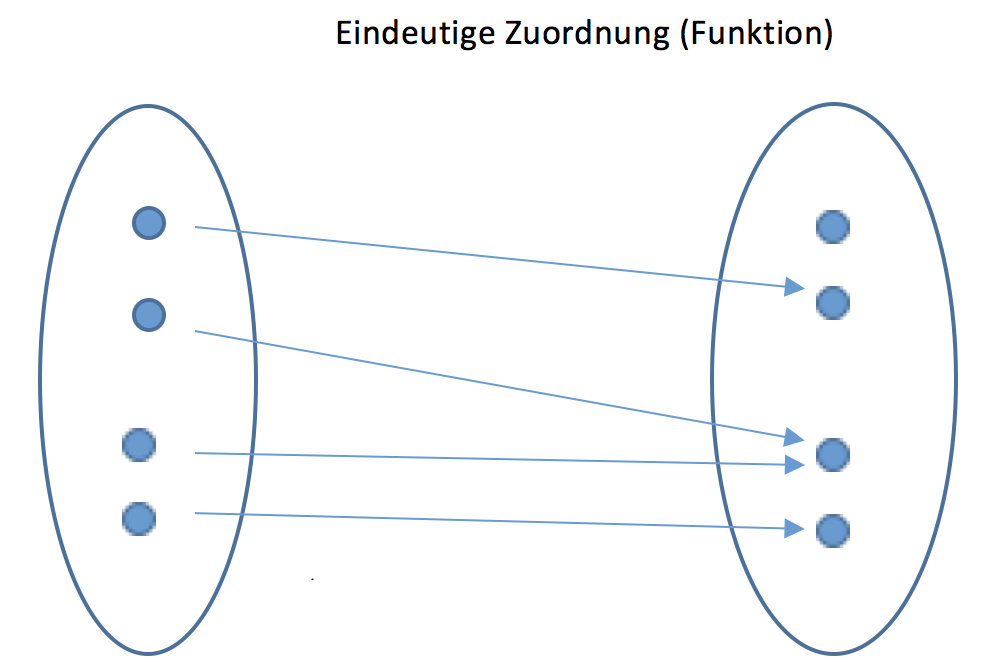
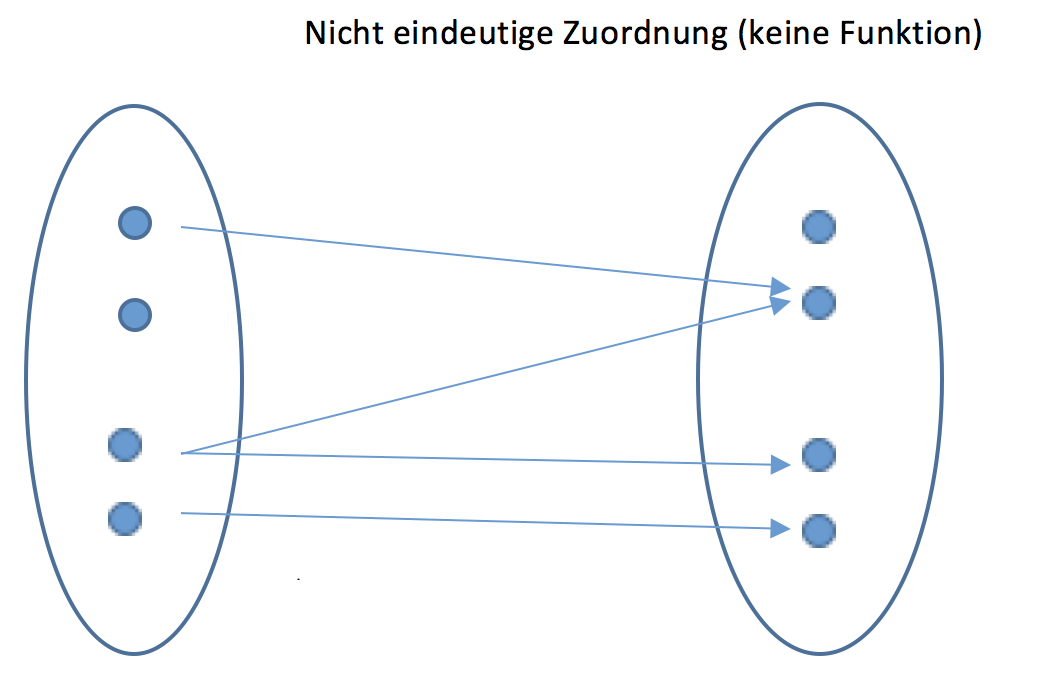
In diesem Beispiel wird jeder natürlichen Zahl \(x\) ihr Quadrat \(y = f(x) = { x }^{ 2 }\) zugeordnet.
Für gewöhnlich werden die hier relevanten Funktionen als Graph in einem Koordinatensystem dargestellt. Beim Graphen handelt es sich, wie oben definiert, um eine Punktemenge, die die bekannte Kurven-Darstellung ergibt. Die Punkte haben die Form \((x|f(x))\) .

Lineare Funktionen
Die Funktionsgleichung einer linearen Funktion \(f : x \in \mathbb{R} \rightarrow f(x) \in \mathbb{R}\) lautet:
\(f(x) = m \cdot x + t \, \) mit \(\, m, \, t \in \mathbb{R}\)
\(m\) wird dabei als Steigung und \(t\) als y-Achsenabschnitt der Funktion (genauer: des Graphen der Funktion) bezeichnet.
Die Graphen linearer Funktionen sind Geraden. Bei positiver Steigung \(m > 0\) „steigt“ die Gerade, bei negativer Steigung \(m < 0\) „fällt“ die Gerade.
Diese Schreibweise bedeutet, dass die Funktionsvorschrift \(f\) einem Wert \(x\) (dem „Urbild“) einen Funktionswert \(f(x)\) (das „Bild“) zuordnet. Sowohl \(x\) als auch \(f(x)\) liegen in diesem Fall in \(\mathbb{R}\).
Je größer der Betrag von \(m\) gewählt wird, desto steiler verläuft die Gerade: Je größer eine positive Steigung ist, desto steiler verläuft sie aufwärts; je kleiner eine negative Steigung, desto steiler verläuft sie abwärts. Analog dazu wird die Gerade für kleinere positive \(m\), bzw. für größere negative \(m\) flacher.
Für \(m=0\) ergibt sich der Sonderfall einer Gerade, die parallel zur \(x\)-Achse, also waagrecht, verläuft:
\(f(x) = t\)
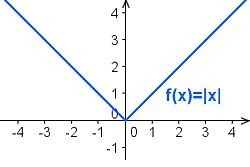
Der Betrag \(|a|\) einer Zahl \(a\) ist deren „Absolutwert“, also ihr Wert „ohne Vorzeichen“: \(|3|=3\) \(|-3|=3\)
Entsprechend kann die Betragsfunktion
\(f(x)=|x|=\begin{cases} x, \text{für } x\geq 0\\ -x, \text{für } x < 0\end{cases}\)
definiert werden:
Man sollte jedoch beachten, dass mit der linearen Funktion keine Geraden dargestellt werden können, die parallel zur y-Achse verlaufen (was der Definition einer Funktion widersprechen würde), da hierzu die Steigung unendlich groß sein müsste und einem einzigen \(x\)-Wert mehrere (unendlich viele) Werte zugeordnet würden.
Derartige Geraden können hingegen mit der folgenden Gleichung (nicht Funktionsgleichung!) dargestellt werden:
\(x=a, a\in \mathbb{R}\)
Da \(t\) unabhängig von \(x\) (\(t\) verändert sich also nicht für verschiedene \(x\)-Werte/ ist für alle \(x\) gleich.) den Funktionswert erhöht oder erniedrigt, kann man durch \(t\) den gesamten Graphen an der \(y\)-Achse entlang verschieben. Für positives \(t\) wird der Graph nach oben und für negatives \(t\) nach unten verschoben. Ist \(t=0\), so verläuft die Gerade durch den Ursprung; es gilt nämlich
\(f(0)=m\cdot 0+t=t=0\).
Man spricht entsprechend von einer Ursprungsgerade.
Untersuchen Sie den Einfluss der Parameter \(m\) und \(t\) auf die lineare Funktion!

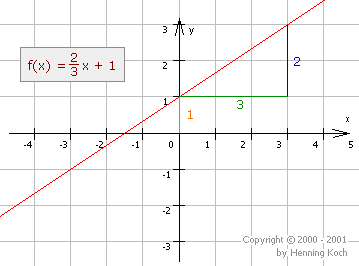
Berechnung der Steigung und des y-Achsenabschnitts
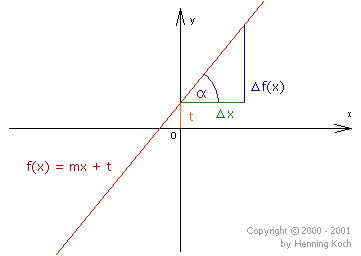
Die Steigung einer linearen Funktion berechnet sich mit Hilfe des Steigungsdreiecks wie folgt:
\(m = \frac{\Delta y}{\Delta x} = \frac{\Delta f(x)}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} \)
Dabei wird der vertikale Abstand zweier Punkte des Graphen durch den horizontalen Abstand der beiden Punkte geteilt (genauer gesagt, die Werte der jeweiligen Abstände). Die Steigung gibt also an, um welchen Wert sich die Funktion vertikal ändert, wenn horizontal eine gewisse Änderung erfolgt.
Ähnlich wird bspw. bei Steigungen im Straßenverkehr verfahren. Es wird gemessen, um wie viele Höhenmeter sich ein Fahrzeug nach oben bewegt, während es sich 100m in der Waagrechten fortbewegt. (Die tatsächlich zurückgelegte Strecke stellt dann die Hypotenuse des entstehenden rechtwinkligen Dreiecks dar.) Auf Grund dieser Idee – \(x\) Höhenmeter pro 100m in der Ebene – wird die entsprechende Steigung in Prozent („pro Hundert“) angegeben.

Der y-Achsenabschnitt \(t\) ist der Wert der Funktion bei \(x=0\), der sich berechnen lässt, indem \(0\) in die Funktionsvorschrift eingesetzt wird:
\(t = f(0)\)
Zeichnen des Funktionsgraphen
Zum Zeichnen des Funktionsgraphen sollte man sich folgende Vorgehensweise einprägen:
- Vom Ursprung aus um \(t\) an der \(y\)-Achse „entlanggehen“. Wir nennen diesen Punkt \(P\).
- Von \(P\) aus um den Wert des Zählers von \(m\) (s. Steigungsdreieck) nach oben und um den Wert des Nenners von \(m\) nach rechts gehen. Wir nennen diesen Punkt \(Q\).
- Der Graph ist eine Gerade durch \(P\) und \(Q\).
Ist \(m\) bereits berechnet worden, so lässt sich als Zähler in obiger Vorgehensweise \(m\) verwenden, als Nenner 1, denn es gilt: \(m = \frac{m}{1}\)
Berechnung des Winkels zwischen Gerade und x-Achse
Wir betrachten das rechtwinkelige Steigungsdreieck. Mit Hilfe der Definition für die Winkelfunktion Tangens im rechtwinkligen Dreieck ((Länge der) „Gegenkathete geteilt durch (Länge der) Ankathete“) gilt:
\(tan(\alpha ) = \frac{\Delta f(x)}{\Delta x} = m\)
nach Definition der Steigung \(m\) und damit
\( \alpha = arctan(m)\)

Nullstellen
Eine lineare Funktion hat genau eine Nullstelle ( \(f(x)=0\) ), also genau einen Schnittpunkt mit der \(x\)-Achse.
Ausgenommen ist der Sonderfall \(m=0\). Damit wäre \(f\) eine konstante Funktion und ihr Graph eine Parallele zur \(x\)-Achse: \(f(x)=t\). Eine solche Funktion hat keine Nullstellen für \(t \neq 0\). Für \(t = 0\) gilt: \(f(x)=0\). In diesem Fall hat die Funktion ausschließlich (und damit unendlich viele) Nullstellen.
Zur Berechnung der Nullstelle \(x_0\) setzt man \(f(x_0)=m\cdot x_0+t = 0\) und löst diese Gleichung nach \(x_0\) auf:
\(x_0 = - \frac{t}{m}\)
Beziehungen zwischen den Graphen einer linearen Funktion
Zwei Geraden sind genau dann parallel, wenn ihre Steigung gleich ist:
\(m_1 = m_2 \Leftrightarrow G_f \parallel G_g\)
Parallele Geraden \(f_1, f_2, f_3,\ldots \) unterscheiden sich also nur durch ihre \(y\)-Achsenabschnitte \(t_1, t_2, t_3,\ldots \) Sie gehen also durch Parallel-Verschiebungen in vertikaler Richtung (nach oben und nach unten) auseinander hervor.
Zwei Geraden \(f=m_1x+t_1\) und \(g=m_2x+t_2\) stehen genau dann aufeinander senkrecht, wenn das Produkt der beiden Steigungen \(-1\) ergibt:
\(m_1 \cdot m_2 = - 1 \Leftrightarrow G_f \bot G_g\)
\(G_f\) bezeichnet den Funktionsgraphen der Funktion \(f\).

Aufgabe:
Begründen Sie diesen Zusammenhang zwischen \(m_1\) und \(m_2\).

Quadratische Funktionen
Die allgemeine Form der quadratischen Funktion \(f : x \rightarrow f(x)\) lautet:
\(f(x) = a \cdot x^2 + b \cdot x + c \, \) mit \( \, a, \,b, \,c \in \mathbb{R}\)
Die Graphen quadratischer Funktionen sind Parabeln. Der Koeffizient („Vorfaktor“) von \(x^2\), also \(a\), bestimmt die Form der Parabel. Bei einem positivem Wert von \(a\) ist die Parabel nach oben, bei einem negativen Wert nach unten geöffnet. Je größer \(|a|\) gewählt wird, desto "enger" wird die Parabel. Analog wird die Form der Parabel für kleineres \(|a|\) weiter. Eine Veränderung des Parameter \(c\) bewirkt eine Verschiebung der Parabel in y-Richtung, denn \(c\) ist unabhängig von \(x\). Veränderungen in \(x\) bewirken also keine Veränderungen in \(c\).
Wird \(c\) um eins erhöht, dann wird der Graph um eine Einheit nach oben verschoben. Wird \(c\) um eins verringert, wird der Graph dagegen um eine Einheit nach unten verschoben.
\(c\) entspricht also sozusagen dem \(y\)-Achsenabschnitt, den wir von den Geraden kennen.
\(|a|\) bezeichnet den Betrag, bzw. Absolutwert von \(a\), also den Wert von \(a\) „ohne negatives Vorzeichen“
\(f(x)=|x|=\begin{cases} x, \text{für } x\geq 0\\ -x, \text{für } x < 0\end{cases}\)
Scheitelpunktsbestimmung
Der Scheitelpunkt der Parabel ist entweder das absolute Minimum (falls \(a\) positiv ist) oder das absolute Maximum (wenn \(a\) negativ ist). Die Koordinaten des Scheitelpunkts lassen sich direkt ablesen, wenn der Funktionsterm mittels quadratischer Ergänzung unter Ausnutzung der binomischen Formeln in die Scheitelpunktsform umgeformt wird:
\(f(x) = a \cdot (x - x_S)^2 + y_S\)
Bei dieser Form der Funktionsgleichung lässt sich der graph von \(f\) als Variation der Normalparabel mit Gleichung \(g(x) = x^2\) interpretieren.
\(f\) entsteht aus dieser durch Verschiebung um \(x_s\) nach rechts, um \(y_s\) nach oben und durch Streckung/Stauchung um den Faktor \(a\).
Als „absolut“ (oder „global“) wird ein Extremum (Maximum oder Minimum) bezeichnet, wenn es sich dabei um den größten/ kleinsten Wert im gesamten Definitionsbereich handelt. Im Gegensatz dazu ist ein „lokales“ Maximum/ Minimum nur Maximum/ Minimum in einer bestimmten Umgebung.
Der Koeffizient \(a\) ändert sich bei der Umformung nicht!
Mit den Koeffizienten der allgemeinen Form für quadratische Gleichungen (s. oben) ergeben sich die Koordinaten des Scheitelpunkts dann zu:
\(x_s = -\frac{b}{2a}\)
\(y_s = -\frac{4ac - b^2}{4a}\)
Der Scheitelpunkt hat dann die koordinaten \(S(x_s|y_s)\). Der Graph von \(f\) ist achsensymmetrisch zu einer Parallelen zur \(y\)-Achse durch \(x_s\).

Zeigen Sie, wie die allgemeine Form \(f(x) = ax^2+ bx + c \,\) in die Scheitelpunktform \(f(x) = a \cdot (x - x_S)^2+ y_S\) überführt werden kann.
Eine quadratische Funktion hat je nach Lage des Scheitelpunktes \(S\) und dem Vorzeichen von \(a\) keine, eine oder zwei Nullstellen.
Zur Berechnung der Nullstellen setzt man \(f(x) = 0\) und löst die Gleichung mittels der quadratischen Lösungsformel:
\(x_{1,2} = \frac{1}{2a} (-b \pm \sqrt{b^2 - 4ac})\)

Aufgabe 1:
Berechnen Sie die Nullstellen der Funktion \(f\) und zeichnen Sie den Funktionsgraphen für \(f(x) = -3x + 6\).
Aufgabe 2:
Gegeben sind zwei Punkte \(P = (4|3)\) und \(Q = (0|-2)\). Bilden Sie die Gleichung der Geraden \(g\) durch \(P\) und \(Q\) und berechnen Sie den Winkel, den \(g\) mit der x-Achse einschließt!
Aufgabe 3:
Bestimmen Sie durch quadratische Ergänzung den Scheitelpunkt \(S\) der Parabel mit \(f(x) = -5x^2+ 30x + 47\).
Aufgabe 4:
Berechnen Sie die Nullstellen folgender Parabel mit \(f(x) = -\frac{1}{2} x^2 + \frac{1}{2} x + 3\).

1.2. Potenzfunktionen, Polynome und Potenzreihen


In diesem Kapitel wiederholen wir zunächst die Eigenschaften von Potenzfunktionen und Polynomen. In einem freiwilligen Exkurs führen wir dann noch ein wichtiges Konzept der Analysis ein - die Potenzreihen.
Potenzfunktionen

Eine Potenzfunktion mit natürlichem Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^n\) mit \(a \in \mathbb{R}, n \in \mathbb{N}, D = \mathbb{R}\)
\(n=1,2,3,\cdots \)
Zwei Spezialfälle einer Potenzfunktion sind uns bereits aus dem letzten Kapitel bekannt:
Für \(n=1\) ergibt sich die reine lineare Funktion \(f\) mit \(f(x) = ax\) un für \(n=2\) ergibt sich die reine quadratische Funktion \(f\) mit \(f(x) = ax^2\).
Außerdem ergibt sich für \(n=0\) der Spezialfall einer konstanten Funktion \(f(x) = a∙x^0 = a∙1 = a\).

Variieren Sie bei folgendem Beispiel für \(f(x) = a \cdot x^3\) den Parameter \(a\). Erläutern Sie die Veränderung des Graphen.

Eine Potenzfunktion mit ganzzahligem Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^z\) mit \(a \in \mathbb{R}, z \in \mathbb{Z}, D = \mathbb{R}\backslash\{0\}\)
\(z=\cdots ,-2,-1,0,1,2,\cdots \)
Die Potenzfunktionen mit ganzzahligem Exponenten lassen sich in zwei Gruppen mit gegensätzlichen Eigenschaften teilen:
\(f(x) = a \cdot x^n\) (natürlicher Exponent, \(n>0\)):
Diese Funktionen haben eine Nullstelle bei \(x = 0\) und divergieren für große \(|x|\) (dh. sie gehen gegen plus unendlich oder minus unendlich). Sie sind auf ganz \(\mathbb{R}\) stetig. Ihre Graphen nennt man Parabeln \(n\)-ter Ordnung.
\(f(x) = a \cdot x^{-n}\) (negativer natürlicher Exponent, \(-n<0\)):
Diese Funktionen haben eine Polstelle bei \(x = 0\) und konvergieren für große \(|x|\) gegen \(0\). Sie sind auf \(\mathbb{R}\backslash\{0\}\) stetig. Ihre Graphen nennt man Hyperbeln n-ter Ordnung. Sie haben auf Grund der Polstelle zwei Äste.
Die Graphen von Potenzfunktionen mit ungeradem Exponent sind punktsymmetrisch zum Ursprung, die von Potenzfunktionen mit geradem Exponent sind achsensymmetrisch zur y-Achse.
\(f(-x) = (-x)^2 = x^2 = f(x)\)
\(f(-x) = (-x)^3 = -(x^3) = -f(x)\)
\(x^{-n} = \frac{1}{x^n}\)
Für wachsende \(x\) wird der Nenner des Bruchs (bzw. eigentlich sein Betrag!) also immer größer und der Gesamtbruch konvergiert gegen 0.

Eine Potenzfunktion mit Stammbruch im Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^{\frac{1}{n}}\) mit \(a \in \mathbb{R}, n \in \mathbb{N}, D = \mathbb{R}_0^+\)
Stammbrüche:
\(\frac{1}{n} = 1,\frac{1}{2},\frac{1}{3},\ldots \)

Unten sehen Sie den Graphen der Funktion \(f\) mit \(f(x) = x^{\frac{1}{n}}\) für \(n \in \{2, 3, 4, 5, 6\}\). Beschreiben Sie den Graphen und achten Sie dabei auf Definitionsbereich, Monotonie, größte und kleinste Funktionswerte. Gibt es Punkte, die allen Graphen dieser Bauart gemeinsam sind? Begründen Sie!
Insbesondere ist die Funktion
\(f: \mathbb{R}_0^+ \rightarrow \mathbb{R}_0^+, x \rightarrow \sqrt{x} = x^{\frac{1}{2}}\),
die jeder positiven Zahl ihre Quadratwurzel zuordnet, eine Potenzfunktion. Analog sind auch die k-ten Wurzeln \( \sqrt[k]{x}\) Potenzfunktionen vermöge der Festlegung \(\sqrt[k]{x} = x^{\frac{1}{k}}\). Die k-te Wurzelfunktion \(f\) mit \(f(x) = x^{\frac{1}{k}} \) ist die Umkehrfunktion zur Potenzfunktion \(g\) mit \(g(x) = x^k\) und \(g\) ist die Umkehrfunktion zu \(f\).

Eine Potenzfunktion mit negativem Stammbruch im Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^{ - \frac{1}{n}}\) mit \(a \in \mathbb{R}, n \in \mathbb{N}, D = \mathbb{R}^+\)

Vergleichen Sie die Graphen der Funktionen mit negativen Stammbrüchen im Exponenten (blau) mit den bereits bekannten Graphen der Funktionen mit poitiven Stammbrüchen im Exponenten (rot gestrichelt). Achten Sie dabei auf Definitionsbereich, Symmetrie, Monotonie, größte und kleinste Funktionswerte. Gibt es Punkte, die allen Graphen gemeinsam sind? Begründen Sie.

Eine Potenzfunktion mit rationalem Exponenten ist eine Funktion der Form:
\(f : x \rightarrow a \cdot x^{\frac{p}{q}}\) mit \(a \in \mathbb{R}, p \in \mathbb{Z}, q \in \mathbb{N}, D = \mathbb{R}^+\)

Vergleichen Sie den Graphen der Potenzfunktionen mit rationalem Exponenten (blau) mit dem, den Sie schon aus den obigen Abschnitten kennen (rot und lila gestrichelt); mit dem Schieberegler können Sie dazu wieder die Exponenten verändern. Beschreiben Sie Gemeinsamkeiten und Unterschiede der Graphen! Achten Sie dabei auf Definitionsbereich und Symmetrie.
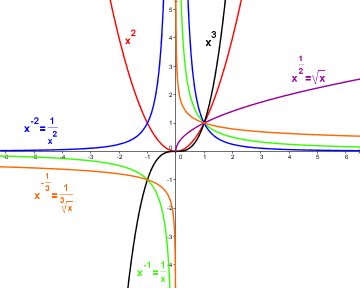 Verschiedene Potenzfunktionen
Verschiedene PotenzfunktionenDie Darstellung von Funktionen der Form \(f(x) = (\sqrt[k]{x})^p\) als \(f(x) = x^{\frac{p}{k}}\) spielt vor allem beim Ableiten von Funktionen eine Rolle, da sich die bekannten Ableitungsregeln damit auch auf Wurzel-Funktionen übertragen lassen.
Polynome werden aus den Potenzfunktionen \(ax^n\) mit natürlichem \(n\) mittels Addition gebildet. Sie sind auf ganz \(\mathbb{R}\) definiert und stetig.

Zu \(a_0, a_1, \ldots, a_n \in \mathbb{R}\) heißt
\(p: \mathbb{R} \rightarrow \mathbb{R}, x \rightarrow \sum_{k=0}^n {a_k x^k} = a_0 + a_1 x + a_2 x^2 + \ldots + a_n x^n\)
Polynom vom Grad \(n\), falls \(a_n \ne 0\).
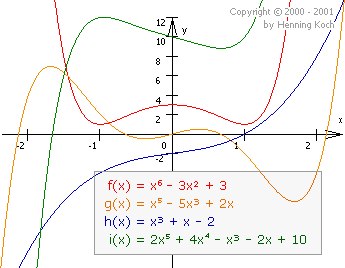 Verschiedene Polynomfunktionen
Verschiedene PolynomfunktionenNach Definition sind also konstante, lineare, quadratische und Potenzfunktionen Polynome.
Die Graphen der Polynome mit Grad \(>2\) besitzen ein nicht mehr so leicht bestimmbares Verhalten und Aussehen wie die Spezialfälle der Graphen konstanter, linearer und quadratischer Funktionen. Um die Eigenschaften dieser Polynome und deren Graphen zu bestimmen, wendet man das aus der Schule bekannte Verfahren der Kurvendiskussion an (siehe rechts).
Polynome bei denen nur gerade Exponenten auftreten sind achsensymmetrisch zur y-Achse, Polynome bei denen nur ungerade Exponenten auftreten sind punktsymmetrisch zum Ursprung.
Polynome sind in der Analysis von großer Bedeutung, da sie eine (relativ) einfache Funktionenklasse darstellen. Insbesondere sind sie leicht zu differenzieren und integrieren. Darüber hinaus gibt es viele Möglichkeiten komplizierte Funktionen durch Polynome anzunähern.
Betrachtet man nun unendliche Summen von Potenzfunktionen, so erhält man "Potenzreihen".

Sei \((a_n)_n\) eine Folge reeller Zahlen und \(x,a \in \mathbb{R}\). Dann heißt die Reihe
\(\sum_{n=0}^\infty {a_n (x-a)^n}\)
Potenzreihe mit Koeffizienten \(a_n\) und Entwicklungspunkt \(a\).
Polynome sind also ein Spezialfall von Potenzreihen, bei denen unendlich viele Koeffizienten \(0\) sind.
Potenzreihen stellen ein mächtiges Werkzeug in der Analysis dar. Im folgenden geben wir zwei Beispiele für Potenzreihen. Ausführlich werden diese in der Analysisvorlesung zu Studienbeginn behandelt.
Die geometrische Reihe
\(\sum_{n=0}^\infty {x^n}\)
konvergiert für alle \(x \in (-1; 1)\). Hier stellt sie die Funktion \(f\) mit
\(f (x) = \frac{1}{1-x}\)
dar.

Zeigen Sie dies, indem Sie für spezielle x-Werte die Summe der ersten \(2, 3, 4, 5, \ldots\) Glieder berechnen.
Die Funktion \(f\) mit
\(f(x) = \sum_{n=0}^\infty {\frac{1}{n!} x^n}\)
ist auf ganz \(\mathbb{R}\) definiert. Mehr zu dieser speziellen Funktion lernen wir im nächsten Kapitel...

Berechnen Sie für spezielle x-Werte die Summe der ersten \(2, 3, 4, 5, \ldots\) Reihenglieder.

- Skizzieren Sie den Verlauf folgender Potenzfunktionen: \(x^3\), \(x^{\frac{1}{3}}\), \(x^{-3}\), \(x^{- \frac{1}{3}}\)
- Geben Sie für die Polynomfunktion mit \(f(x) = - \frac{1}{4} x^4 + \frac{3}{2} x^2 - 2x -2\) Art und Lage der Extrempunkte, die Wendepunkte und die Nullstellen an.

1.3. Exponentialfunktion und Wachstum


In diesem Kapitel lernen wir eine besonders wichtige Funktion kennen - die Exponentialfunktion. Danach werden wir das Wachstum beliebiger Funktionen an Hand des Wachstums bereits bekannter Funktionen kategorisieren.
Einführendes Beispiel: Lineares und exponentielles Wachstum
Kapitalentwicklung bei einfacher Verzinsung
Bei einer einfachen Verzinsung werden in jedem Jahr nur die einfachen Zinsen in der Höhe von \(K_0 \cdot \frac{p}{100}\) zum Anfangskapital \(K_0\) hinzugerechenet. Die Zinsen der weiteren Jahre werden immer nur vom Anfangskapital \(K_0\) berechnet. Es wird also davon ausgegangen, dass die jährlichen Zinsen an den Anleger ausbezahlt werden. Es ergibt sich für das Kapital nach \(n\) Jahren
\(K(n) = K_0 + K_0 \cdot \frac{p}{100} \cdot n\)
Kapitalentwicklung mit Zinseszins
Bei einer Verzinsung mit Zinseszinsen werden jedes Jahr die Zinsen der vorangegangenen Jahre wiederum verzinst, d.h. das Anfangskapital \(K_0\) wird im jedem Jahr mit \((1 + \frac{p}{100})\) multipliziert. Es ergibt sich für das Kapital nach \(n\) Jahren
\(K(n) = K_0 \cdot (1 + \frac{p}{100})^n\)

Erläutern Sie das Zustandekommen dieser Formel.
Näherungsweise kann man aber auch mit einem Exponenten \(x \in \mathbb{R}\) arbeiten, um das Kapital zu beliebigen Zeitpunkten (z.B. \(x = 1, 75\) Jahre) zu berechnen. Der Graph für das Kapital nach einer beliebigen Zeitspanne \(x\) besteht in diesem Fall aus einer stetigen Kurve. (Diese kontinuierliche Entwicklung kann in den Applets über das Kontrollkästchen ein- bzw. ausgeschaltet werden.)
Das Anwachsen eines Kapitals nach der Funktionsgleichung \(K(x) = K_0 \cdot (1 +\frac{p}{100})^x\) nennt man exponentielles Wachstum. Dieses Wachstum wird durch die Funktionsgleichung eines neuen Funktionstyp beschrieben. Bei dieser Art von Funktion steht die unabhängige Variable \(x\) im Exponenten und wird deshalb Exponentialfunktion genannt.
Die allgemeine Exponentialfunktion

Die Funktion
\(f: \mathbb{R} \rightarrow \mathbb{R}, \, f(x) = a^x = \exp (x \cdot \log(a))\,\) für \(a \in \mathbb{R}^+\)
heißt Exponentialfunktion zur Basis \(a\).
\(a>0\) wird hier echt positiv gewählt, da für \(a<0\) bspw. Ausdrücke der Form \(a^{\frac{1}{2}}=\sqrt{a}\) in \(\mathbb{R}\) nicht lösbar sind.
Für \(a=0\) hingegen sind bspw. Ausdrücke der Form \(a^{-1}=\frac{1}{a}\) nicht definiert.

Für alle \(x,y \in \mathbb{R}\) gilt:
\(a^{(x+y)} = a^x \cdot a^y\)

- Die Exponentialfunktion ist für alle \(x \in \mathbb{R}\) definiert.
- Sie nimmt nur positive Funktionswerte an.
- Die Graphen aller Exponentialfunktionen der Form \(f(x) = a^x\) gehen durch den Punkt \((0|1)\).
- Für \(0 < a < 1\) ist \(f(x)\) monoton fallend, für \(a = 1\) konstant und für \(a > 1\) monoton steigend.
- Die Graphen von \(f(x) = a^x\) und \(g(x) = a^{-x}=\frac{1}{a^x}\) liegen symmetrisch bezüglich der y-Achse. Für beide Graphen ist die x-Achse horizontale Asymptote.
- Für \(0 < a < 1\) ist \(f(x) = a^x\) monoton fallend, \(f\) divergiert für \(x \rightarrow -\infty\) und konvergiert gegen \(0\) für \(x \rightarrow \infty\)
- Für \(a=1\) ist \(f\) konstant
- Für \(a > 1\) ist \(f(x) = a^x\) monoton steigend, \(f\) divergiert für \(x \rightarrow \infty\) und konvergiert gegen \(0\) für \(x \rightarrow -\infty\)
Es gilt: \(a^0=1\) für alle \(a\)
Es gilt: \(1^x=1\) für alle \(x\)
\(f(-x) = a^{-x} = g(x)\)
\(f(x) = a^{x} = a^{-(-x)} = g(-x)\)

- (Diskussion von \(x \rightarrow a^x\)) Stellen Sie zunächst für \(m\) und \(b\) den Wert \(1\), für \(c\) und \(d\) den Wert \(0\) ein und ändern Sie mit Hilfe des Schiebereglers den Wert der Basis \(a\) und beschreiben Sie den Verlauf des Schaubildes für verschiedene Werte von \(a\). Verifizieren Sie die oben genannten Eigenschaften der Funktion \(x \rightarrow a^x\).
- Warum existiert die Funktion \(f(x)\) nicht für negative \(a\)?
- (Diskussion von \(x \rightarrow m \cdot a^x\)) Lassen Sie wiederum \(a\) fest (nicht \(0\)) und veränderen Sie nur \(m\). Beschreiben Sie die Auswirkungen auf das Schaubild und finden Sie eine bestimmte Eigenschaft für bestimmte Wertepaare von \(m\) heraus.
- (Diskussion von \(x \rightarrow a^{b \cdot x}\)) Lassen Sie nun \(a\) fest (nicht \(0\)) und verändern Sie nur \(b\). Beschreiben Sie die Auswirkungen auf das Schaubild und finden Sie eine bestimmte Eigenschaft für bestimmte Wertepaare von \(b\) heraus.
- (Diskussion von \(x \rightarrow a^x+ c\)) Stellen Sie für \(m\) und \(b\) wieder den Wert \(1\) und für \(d\) den Wert \(0\) ein und ändern Sie mit Hilfe des Schiebereglers den Wert von \(c\). Beschreiben Sie die Auswirkungen auf das Schaubild.
- (Diskussion von \(x \rightarrow a^{x+d}\)) Stellen Sie für \(m\) und \(b\) wieder den Wert \(1\) und für \(c\) den Wert \(0\) ein und ändern Sie mit Hilfe des Schiebereglers den Wert von \(d\). Beschreiben Sie die Auswirkungen auf das Schaubild.
Beispiel 2 (Die Exponentialfunktion wächst schneller als jede Potenz von x):
Für beliebiges \(m \in \mathbb{N}\) gilt \(x^m < o(\exp(x))\), denn für \(x > 0\) ist
\(\exp(x) = \sum_{n=0}^\infty {\frac{x^n}{n!}} > \frac{x^{m+1}}{(m+1)!}\)
und damit
\( 0 \ge \lim_{x \to \infty} \frac{x^m}{\exp(x)} \ge \lim_{x \to \infty} \frac{x^m}{\frac{x^{m+1}}{(m+1)!}} = 0\)
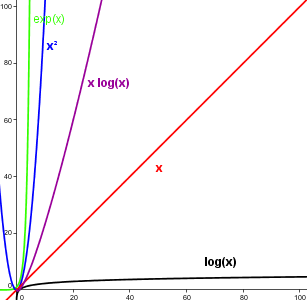
Der Logarithmus - die Umkehrfunktion der Exponentialfunktion
Die Umkehrfunktion der Exponentialfunktion ist der Logarithmus \(\log_a(x) : \mathbb{R}^+ \rightarrow \mathbb{R}\). Er ist stetig und streng monoton wachsend.
Die Logarithmus-Funktion ergibt sich als Umkehrfunktion durch Umformen der Exponentialfunktion:
\(y=f(x)=a^x\)
Dann ist:
\(x=f^{-1}(y)=log_a(y)\)
Um die Funktion im gewohnten Koordinatensystem darzustellen, wird sie allerdings ebenfalls in der Form \(x \rightarrow f^{-1}(x)\) verwendet.

- Ändern Sie mit Hilfe des Schiebereglers den Wert von \(a\) und beschreiben Sie den Verlauf des Schaubildes für verschiedene Werte von \(a\). Was haben alle Funktionen gemeinsam? Welche Unterschiede für welche \(a\) gibt es?
- Was fällt Ihnen im Vergleich von Exponentialfunktion und Logarithmusfunktion auf? Beschreiben Sie die Lage beider Schaubilder zueinander.

Für alle \(x, y \in \mathbb{R}^+\) gilt:
\(\log_a(x \cdot y) = \log_a(x) + \log_a(y)\)


1.4. Trigonometrische Funktionen


Nun sollen die wichtigsten Eigenschaften der trigonometrischen Funktionen (oft auch Winkelfunktionen genannt) Sinus (\(\sin\)), Cosinus (\(\cos\)) und Tangens (\(\tan\)) erläutert werden.
Die trigonometrsichen Funktionen beschreiben Zusammenhänge zwischen den Seiten und Winkeln eines rechtwinkligen Dreiecks. Als Hypotenuse bezeichnet man die dem rechten Winkel gegenüber liegende Seite des Dreiecks. Die Gegenkathete ist die Seite des Dreiecks, die dem Winkel gegenüber liegt, der gerade betrachtet wird. Die Ankathete ist die direkt am Winkel anliegende Seite (die nicht die Hypotenuse ist).
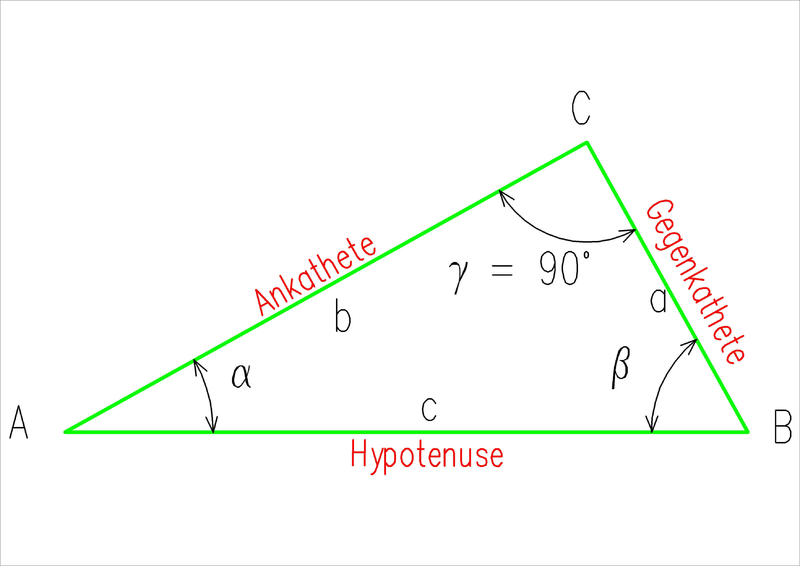 rechtwinkliges Dreieck
rechtwinkliges DreieckDie Trigonometrischen Funktionen sind am rechtwinkeligen Dreieck wie folgt definiert:
Sinus
Der Sinus ist das Verhältnis der Längen von Gegenkathete und Hypotenuse.

\(\sin(\alpha) = \frac {Gegenkathete}{Hypotenuse}\)
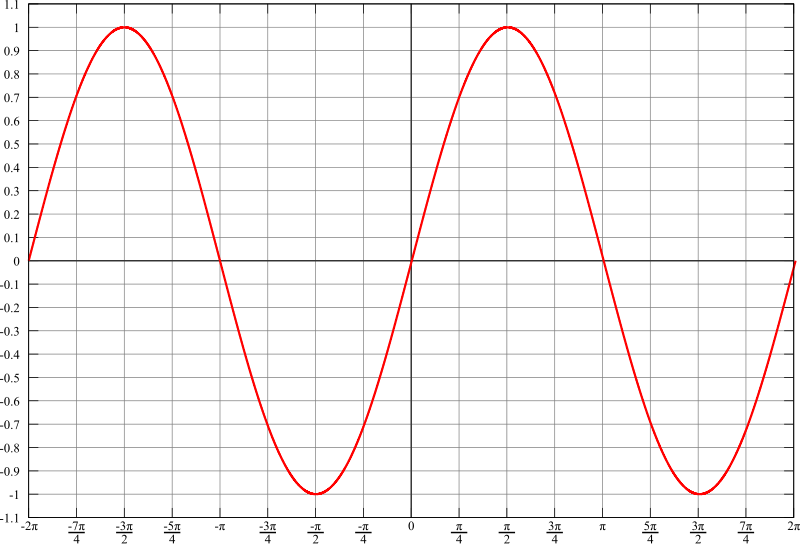 Sinusfunktion
SinusfunktionDer Begriff Sinus stammt aus dem Lateinischen für Bogen, Krümmung.
Da in der Geometrie die Hypotenuse immer die längste Seite im Dreieck ist, ist der Wert des Sinus immer kleiner \(1\).
Der Cosinus ist das Verhältnis der Längen von zwischen Ankathete und Hypotenuse.

\(\cos(\alpha) = \frac {Ankathete}{Hypotenuse}\)
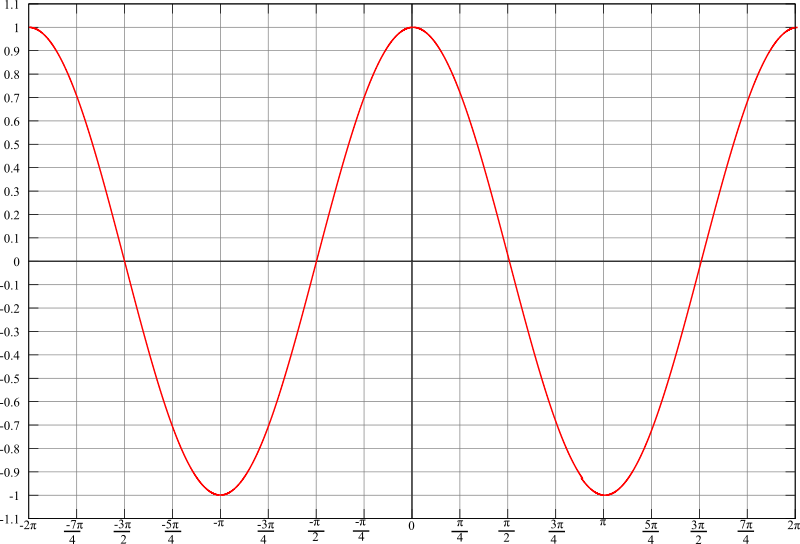 Cosinusfunktion
CosinusfunktionDie Bezeichnung Cosinus ergibt sich aus complementi sinus, also dem Sinus des Komplementärwinkels.
Für den Cosinus gilt natürlich auch, dass der Wert immer kleiner \(1\) ist, da die Hypotenuse die längste Seite ist.
Der Tangens ist das Verhältnis der Längen von Gegenkathete zu Ankathete.

\(\tan(\alpha) = \frac {\sin(\alpha)}{\cos(\alpha)} = \frac{\frac{Gegenkathete}{Hypotenuse}}{\frac{Ankathete}{Hypotenuse}} = \frac{Gegenkathete}{Ankathete}\)
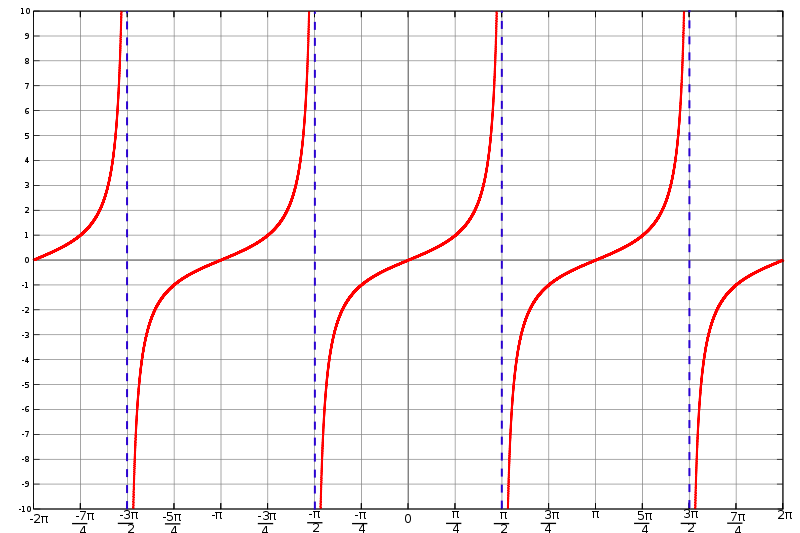 Tangensfunktion
TangensfunktionDer Name Tangens lässt sich aus der Definition des Tangens am Einheitskreis ableiten. Näheres dazu im nächsten Kapitel.
Der Wert des Tangens kann \(1\) leicht überschreiten, da zum einen im Verhältnis die Hypotenuse nicht mehr vorkommt (was beim Sinus und Cosinus der Grund für die Wertgrenze war), und zum anderen die Ankathete durchaus kleiner sein kann als die Gegenkathete.
Zeichnet man in einem Koordinatensystem den Einheitskreis um den Ursprung (Nullpunkt) und wählt im ersten Quadranten einen Punkt \(P\) auf dem Einheitskreis, so kann man ein rechtwinkliges Dreieck in den Einheitskreis dermaßen einzeichnen, dass die Strecke vom Nullpunkt zu \(P\) als Hypotenuse anzusehen ist.
\(x\) ist dann also die x-Koordinate von \(P\) und \(y\) die y-Koordinate.
Somit kann man \(\sin\), \(\cos\) und \(\tan\) wieder mittels der obigen Definitionen bestimmen. Da die Hypotenuse in diesem Fall genau die Länge \(1\) hat, ergeben sich für den Sinus und Cosinus die Werte
\(\sin(\alpha) = y\) und \(\cos(\alpha) = x\)
Mit Hilfe des Satzes von Pythagoras erhält man die Gleichung
\(\sin^2(\alpha) + \cos^2(\alpha) = 1\)
Verlängert man die Strecke \(\overline{0P}\) über \(P\) hinaus und zeichnet im Punkt \((1,0)\) eine Tangente an den Einheitskreis (diese verläuft dann senkrecht), so entspricht der Tangens der Strecke zwischen dem Punkt \((1,0)\) und dem Schnittpunkt der Urspungsgeraden durch \(P\) und der Tangente. Aus dieser Beziehung folgt auch der Name Tangens. Wählt man den Punkt \(P\) auf dem Einheitskreis aber außerhalb des ersten Quadranten, so ergeben sich für den Sinus, Cosinus und Tangens auch die Werte für beliebige Winkel.
Dabei lassen sich folgende Beziehungen erkennen:
\(-\sin(\alpha) = \sin(-\alpha)\)
\(cos(-\alpha) = \cos (\alpha)\)
Der Sinus ist also eine ungerade (der Graph ist punktsymmetrisch zum Ursprung) Funktion, der Cosinus eine gerade (der Graph ist achsensymmetrsich zur y-Achse) Funktion.
Man erkennt auch, dass Sinus und Cosinus periodische Funktionen sind mit der Periode \(360°(= 2\pi)\).
Der Tangens ist ebenfalls periodisch, da gilt:
\(\tan(\alpha + 180°) = \frac{\sin(\alpha + 180°)}{\cos(\alpha + 180°)} = \frac{-\sin(\alpha)}{-\cos(\alpha)} = \tan(\alpha)\)
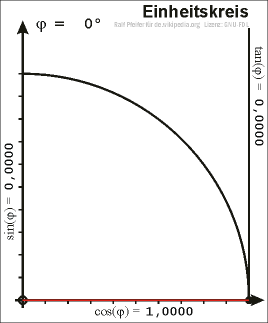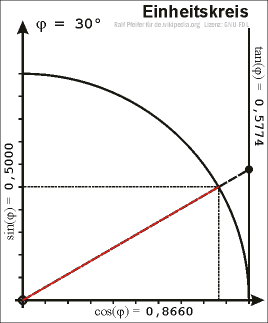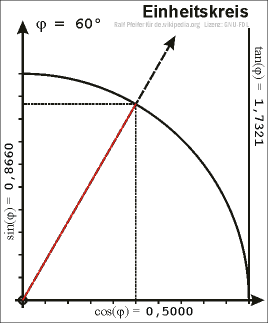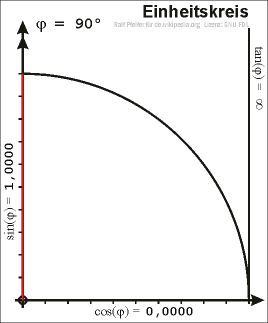 rechtwinkliges Dreieck im Einheitskreis
rechtwinkliges Dreieck im EinheitskreisDie allgemeine Form der Trigonometrischen Funktionen \(\sin\), \(\cos\) und \(\tan\) kann man folgendermaßen angeben:
\(\sin(\alpha) = a \cdot \sin(b \cdot \alpha - c) + d\)
\(\cos(\alpha) = a \cdot \cos(b \cdot \alpha - c) + d\)
\(\tan(\alpha) = a \cdot \tan(b \cdot \alpha - c) + d\)
Der Faktor \(a\) verändert hier die Auslenkung in y-Richtung. Es gilt:
| \(a = 1\) | die "normale" Funktion wird angegeben |
| \(a<1\) | die Amplitude ist schwächer |
| \(a>1\) | die Amplitude ist stärker |
Der Faktor \(b\) verändert die Periode der Funktion. Es gilt:
| \(b = 1\) | die "normale" Funktion wird angegeben |
| \(b<1\) | die Periode wird seltener |
| \(b>1\) | die Periode wird häufiger |
Der Faktor \(c\) verschiebt den Graph der Funktion in x-Richtung. Es gilt:
| \(c = 0\) | die "normale" Funktion wird angegeben |
| \(c<0\) | Verschiebung nach links |
| \(c>0\) | Verschiebung nach rechts |
Der Faktor \(d\) verschiebt den Graph der Funktion in y-Richtung. Es gilt:
| \(d = 0\) | die "normale" Funktion wird angegeben |
| \(d<0\) | Verschiebung nach unten |
| \(d>0\) | Verschiebung nach oben |

Für alle \(x \in \mathbb{R}\) gilt:
\(\cos(x) = \sum_{k=0}^\infty {(-1)^{k} \frac{x^{2k}}{(2k)!}}\)
\(\sin(x) = \sum_{k=0}^\infty {(-1)^{k} \frac{x^{2k+1}}{(2k+1)!}}\)

Die Umkehrfunktionen von \(\sin\), \(\cos\) und \(\tan\) lauten wie folgt:
Arcuscosinus: \(\arccos: [-1, 1] \rightarrow \mathbb{R}\)
\(\arccos(x) = \cos^{-1}(x)\)
Arcussinus: \(\arcsin: [-1, 1] \rightarrow \mathbb{R}\)
\(\arcsin(x) = \sin^{-1}(x)\)
Arcustangens: \(\arctan: \mathbb{R} \rightarrow \mathbb{R}\)
\(\arctan(x) = \tan^{-1}(x)\)
| Winkel | \(0°\) | \(30°\) | \(45°\) | \(60°\) | \(90°\) | \(180°\) | \(270°\) |
| Bogenmaß | \(0\) | \(\frac{\pi}{6}\) | \(\frac{\pi}{4}\) | \(\frac{\pi}{3}\) | \(\frac{\pi}{2}\) | \(\pi\) | \(\frac{3 \pi}{2}\) |
| Sinus | \(0\) | \(\frac{1}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(1\) | \(0\) | \(-1\) |
| Cosinus | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{1}{2}\) | \(0\) | \(-1\) | \(0\) |
| Tangens | \(0\) | \(\frac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | Pol | \(0\) | Pol |

Skizzieren Sie den Verlauf der Graphen der Funktionen für \(x \in [0, 2\pi]\).
- \(\sin(2x) + 3\)
- \(\frac{\cos(x) - 2}{\sin(x)+2}\)
- \(\frac{1}{2} \cdot \tan(3x)\)
Aufgabe 2:
Bestimmen Sie die Nullstellen der in Aufgabe 1 genannten Funktionen.
Aufgabe 3:
Gegeben sei ein rechtwinkliges Dreieck mit der Hypotenusenlänge \(3\) und dem Winkel \(\alpha = 37°\). Bestimmen Sie die Länge der beiden Katheten.

1.5. Aufgaben


Aufgabe 1: Parabeln I
Die Graphen der Funktionen \(f\), \(g\) mit \(f(x) = ax^2+ bx + c\) und \(g(x) = d(x-e)^2+ h\) sollen dieselbe Parabel darstellen. Welche Beziehung besteht zwischen den Variablen \(a\), \(b\), \(c\), \(d\), \(e\) und \(h\)?
Aufgabe 2: Parabeln II
Wir betrachten die Parabeln \(P_b\) mit der Gleichung \(f(x) = 2x^2+ bx + 1\), \(b \in \mathbb{R}\).
- Bestimmen Sie den Scheitelpunkt \(S_b\) der Parabeln \(P_b\) (also in Abhängigkeit von \(b\)).
- Zeichnen Sie – etwa mit Hilfe des Programms GeoGebra (kostenlos downloadbar unter http://www.geogebra.at) – die Ortslinie \(OS_b\), auf der sich der Scheitelpunkt von \(P_b\) bewegt, wenn \(b\) variiert wird. In die Lösung der Aufgabe soll ein Screenshot dieser Aufgabe eingebunden werden.
- Bestimmen Sie die Gleichung für die Ortslinie \(OS\).
Aufgabe 3: Exponentialfunktion
- Vergleichen Sie die beiden Funktionen mit \(y = a \cdot 2^x\) und \(y = 2^{(x+d)}\) für verschiedene Werte \(a,d \in \mathbb{R}\). Für welche \(a\) bzw. \(d\)-Werte stimmen die Graphen der beiden Funktionen überein?
- Die allgemeine Exponentialfunktion lässt sich mit der Gleichung \(f(x) = a \cdot b^{cx+d}\) mit \(a,c,d \in \mathbb{R}; b \in \mathbb{R}^+\) beschreiben. Diese Gleichung ist äquivalent zu einer Gleichung mit nur drei Parametern \(A,B,C\), wobei \(A,B,C \in \mathbb{R}\) bzw. \(\mathbb{R}^+\). Geben Sie den Zusammenhang zwischen \(A,B\) und \(C\) sowie \(a,b,c\) und \(d\) an!
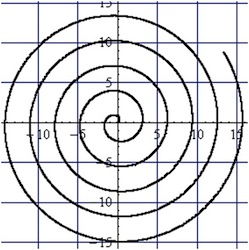
Zeichnen Sie die Kurve \(K(t) = (t \cdot \cos(t), t \cdot \sin(t))\) für \(0 < t < 20\). Die Kurve lässt sich aus einer Bewegung entstanden denken und dynamisch interpretieren, indem \(t\) als Zeit verstanden wird. Man nennt diese Kurve Spirale.
- Beschreiben Sie diese Bewegung!
- Geben Sie die Gleichung abgebildeten Spirale an!
Gegeben ist eine Ellipse \(E(x,y): \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\); \(a,b \in \mathbb{R}^+\). Geben Sie die Gleichung der Tangente an die Ellipse im Ellipsenpunkt \(P(x_0,y_0)\) an.
Hinweis: Gehen Sie vom Kreis \(K_a: x^2+ y^2= a^2\) aus und erzeugen Sie \(E\) durch eine Streckung bzw. Stauchung von \(K_a\) mit dem Faktor \(\frac{b}{a}\) parallel zur y-Achse. Gehen Sie dann von einer Kreistangente aus.
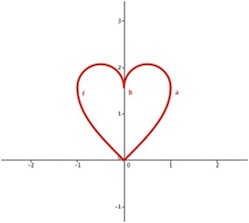
Es gibt verschiedene Möglichkeiten, ein Herz mit Hilfe von mathematischen Funktionen zu zeichnen. Insbesondere kann ein Herz sehr unterschiedliche Formen besitzen. Zeichnen Sie aus Funktionsstücken (mit GeoGebra) ein Herz. Das Bild rechts zeigt eine Möglichkeit der Umsetzung.
- Beschreiben Sie den Graphen \(G\) der Funktion mit \(f(x,y) = x^2+ y^2\), indem Sie \(G\) mit ausgewählten Ebenen schneiden und die Schittfiguren beschreiben.
- Wir betrachten die beiden Ebenen im Raum mit \(f(x,y) = 4x + y + 3\) und \(g(x,y) = -x + 3y - 5\) in einem gemeinsamen Koordinatensystem. Zeigen Sie, dass die beiden Ebenen zueinander senkrecht sind.

2. Ausblick: Inhalte des vhb-Kurses
- 1. Funktionen
-
1.1. Lineare und quadratische Funktionen
-
1.2. Potenzfunktionen, Polynome und Potenzreihen
-
1.3. Exponentialfunktion und Wachstum
-
1.4. Trigonometrische Funktionen
-
1.5. Funktionen mehrerer Veränderlicher
-
1.6. Kurven und Abbildungen
-
1.7. Aufgaben
-
-
2. Folgen und Grenzwerte
-
2.1. Einführung in Folgen
-
2.2. Wie kann eine Folge definiert werden?
-
2.3. Wichtige Beispiele für Folgen
-
2.4. Elementare Eigenschaften von Folgen
-
2.5. Grenzwerte von Funktionen
-
2.6. Rechnen mit Grenzwerten
-
2.7. Stetigkeit von Funktionen
-
2.8. Eigenschaften stetiger Funktionen
-
2.9. Aufgaben
-
-
3. Gleichungen
-
3.1. Grundlegende Konzepte und Lösungsmethoden
-
3.2. Lineare und Quadratische Gleichungen
-
3.3. Trigonometrische Gleichungen
-
3.4. Exponentielle und Logarithmische Gleichungen
-
3.5. Komplexe Zahlen
-
3.6. Aufgaben
-
-
4. Ableitung
-
4.1. Grundlagen
-
4.2. Eigenschaften von Ableitungen
-
4.3. Ableitungen der trigonometrischen Funktionen
-
4.4. Die Kettenregel
-
4.5. Die Exponentialfunktion und der Logarithmus
-
4.6. Extremwert-Probleme
-
4.7. Aufgaben
-
-
5. Integration
-
5.1. Der Begriff
-
5.2. Hauptsatz der Differential- und Integralrechnung
-
5.3. Integrale elementarer Funktionen
-
5.4. Integrationstechniken
-
5.5. Anwendungen
-
5.6. Aufgaben
-
-
6. Differentialgleichungen
-
6.1. Begriffe
-
6.2. Lösen gewöhnlicher Differentialgleichungen erster Ordnung
-
6.3. Gewöhnliche Differentialgleichungen zweiter und höherer Ordnung
-