Lecture - Image Processing
3. Basic Methods II: Image operations
3.3. Geometric Operations - Rotation
In order to match an image to another image or coordinate system with different orientation it needs to be rotated. With the rotation angle \( \theta \) the equations for the new coordinates of a pixel are described by:
\( x' = x \cos \theta - y \sin \theta \)
\( y' = x \sin \theta + y \cos \theta \)
in a counterclockwise rotation. In an analogous formulation, the position of every pixel \( (x',y') \) in the new image can be written as a vector and the rotation matrix:
\( \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \)
In this simple case the point of rotation \( (x_0, y_0) \) is the point of origin of the coordinate system \( (0,0) \). Quite more useful and practical is the rotation around a certain point of the image or the center of the image, as depicted in Fig. 3.2. In order to rotate a pixel at \( (x, y) \) around an arbitrary point \( (x_0, y_0) \) the equations become:
\( x' = x_0 + (x - x_0) \cos \theta + (y - y_0) \sin \theta \)
\( y' = y_0 - (x - x_0) \sin \theta + (y - y_0) \cos \theta \)
The only pixel that does not move from its position is the pixel at \( (x_0, y_0) \) itself. Again, if the new image is being calculated form the old one, the equations that describe the rotation need to be solved for \( x \) and \( y \), i.e. the inverse transform is needed. The values of all pixels of the rotated image need to be interpolated from the pixel values of the old image in most cases. Therefore, equations for \( x \) and \( y \) that access the values of all four (old) surrounding pixels at the position of the new pixel are required.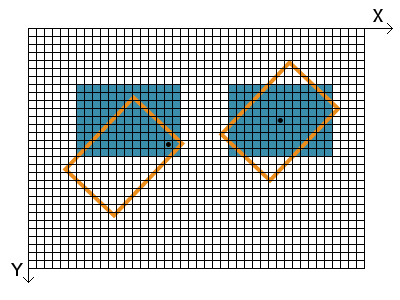
Fig. 3.2: Rotation of an image. The black dots indicate \( (x_0, y_0) \), the center of rotation in each case.
