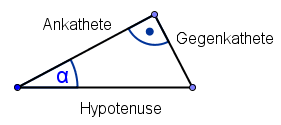
- Diese Erkenntnis soll im nächsten Schritt über Ähnlichkeiten oder Strahlensätze gesichert werden.
Demokurs: Didaktik der Geometrie
Requisitos de conclusão
Kursbuch
1. Trigonometrie I
1.2. Einführung von Sinus, Kosinus und Tangens am rechtwinkligen Dreieck
Meistens wird in den Lehrbüchern zuerst der Sinus eingeführt, in manchen wird aber auch mit dem Tangens begonnen (was sinnvoll erscheint, da die Frage nach dem Zusammenhang zwischen Anstieg (Steigung) und Steigungswinkel bereits seit der Behandlung der linearen Funktionen offen ist).
Zum Einstieg in die Trigonometrie am rechtwinkligen Dreieck sollten zunächst Anwendungsprobleme gewählt werden, die bereits in früheren Schuljahren durch maßstäbliche Darstellungen konstruktiv bearbeitet werden konnten. Derartige Anwendungen können nun die exakte rechnerische Bestimmung fehlender Größen in rechtwinkligen Dreiecken motivieren.
Im Folgenden werden zwei Anwendungssituationen vorgestellt, welche die Einführung von Sinus und Tangens motivieren können:
Anwendungssituation zur Einführung des Sinus: Der Kran
Der Ausleger eines Krans sei 9,5 m lang und kann bis auf eine Länge von 35 m ausgefahren werden. Man kann ihn bis zu einem Winkel von höchstens 80° gegen die Waagerechte aufrichten. Mit Hilfe des Winkels und der Länge des Auslegers kann die Tragkraft des Krans kalkuliert und die Hubhöhe eingestellt werden, um die die Last angehoben werden kann.
Machen Sie sich mit Hilfe des Applets mit der Bedienung des Krans in Bezug auf die Hubhöhe vertraut. Von welchen Größen ist sie abhängig?
Anwendungssituation zur Einführung des Tangens: Straßensteigung
Straßensteigungen und -gefälle werden auf Verkehrsschildern in Prozent angegeben. Als steilste Straße der Welt gilt die Baldwin Street in Neuseeland mit einer maximalen Steigung von ca. 35%. Automobilkonzerne werben damit, dass ihre PKW-Topmodelle 80 oder sogar 100 Prozent Steigung bewältigen können.
Machen Sie sich mit Hilfe des Applets mit dem Begriff Steigung vertraut und erklären Sie, wie die Angabe von z.B. 80% entstehen kann.
Nach der Diskussion einführender Beispiele sollten die Verhältnisse in rechtwinkligen Dreiecken weiter erkundet bzw. gesichert werden, bevor die Begriffe Sinus, Kosinus und Tangens eingeführt werden:
- Im zweiten Schritt muss die Erkenntnis gewonnen bzw. gesichert werden, dass in einem rechtwinkligen Dreieck das Verhältnis zweier Seitenlängen nur von der Größe eines Winkels abhängt. Die eindeutige Zuordnung zwischen Streckenverhältnissen und Winkeln lässt sich durch experimentelles Arbeiten mit einem DGS unterstützen.
- Am Ende der Einführungssequenz steht dann die Definition der Begriffe Sinus, Kosinus und Tangens. Dafür sollten die einführenden Beispiele wieder aufgegriffen werden:
In Bezug auf das Anwendungsbeispiel "Der Kran" soll sich herausstellen, dass das Verhältnis zwischen der Hubhöhe und der Auslegerlänge allein vom Winkel α abhängt und dass es mit der Winkelfunktion Sinus bezeichnet wird: \[ \sin \alpha =\frac{Hubh\ddot{o}he}{Auslegerl\ddot{a}nge} \] Damit lässt sich also durch Wahl des Winkels und der Länge des Auslegers eine bestimmte Hubhöhe eindeutig einstellen. Das Anwendungsbeispiel "Straßensteigung" führt auf die Definition der Winkelfunktion Tangens: \[ \tan \alpha =\frac{H\ddot{o}hengewinn}{Luftlinie}\] Der Wert entspricht der Prozentangabe auf den Straßenschildern. Zu der Straße mit der steilsten Steigung von 35% gehört also ein Steigungswinkel von "nur" \( \alpha ={{\tan }^{-1}}(0,35)=19,29{}^\circ \).
