Einführung, Fächer der Psychologie

Die Geschichte der Persönlichkeits- und Differentiellen Psychologie ist vor allem eine Geschichte der Intelligenzforschung. Als Begründer dieser Forschung gelten Franz Joseph Gall (1758-1828), der etwa Ende des 18. Jahrhunderts die Verbindung zwischen geistigen Leistungen und der Schädelform untersuchte, sowie Sir Francis Galton (1822-1911), der wie James McKeen Cattell (1860-1944) Testverfahren zur Erfassung psychischer Eigenschaften entwickelte und ebenfalls versuchte, die erbbiologischen Gesetzmäßigkeiten der Intelligenz zu entschlüsseln. Ein Meilenstein der Intelligenzforschung war jedoch die Entwicklung der ersten Intelligenztests durch Alfred Binet (1857-1911) zusammen mit Theophile Simon (1873-1961). Binet war Mitglied der Kommission zur Früherkennung und Förderung von Kindern mit intellektuellen Schwierigkeiten. Als das Pariser Unterrichtsministerium verfügte, dass Kinder nur in Sonderschulen eingewiesen werden dürfen, wenn die Einweisung gestützt auf ein medizinisch-pädagogisches Gutachten erfolgt, wollte er ein Verfahren schaffen, um objektiv alle betroffenen Schüler zu ermitteln.                                                                            

Zunächst (1905) stellten Binet und Simon insgesamt 30 Aufgaben vor, mit deren Hilfe in einem Probelauf 30 minderbegabte von 50 normalen Kindern unterschieden werden konnten (Amelang & Bartussek, 1997). Diese ursprüngliche Serie wurde 1908 und 1911 verbessert, sodass für jede Altersstufe von 3 bis 10 Jahren inhaltlich heterogene und unterschiedlich schwierige Aufgaben so zusammengestellt wurden, dass sie von etwa 50-75% der Kinder der Altersstufe gelöst werden konnten (s. auch Abb. 1.2). Geeignet waren danach solche Aufgaben, die von möglichst vielen Altersgenossen, aber nicht von deutlich jüngeren Kindern gelöst werden konnten.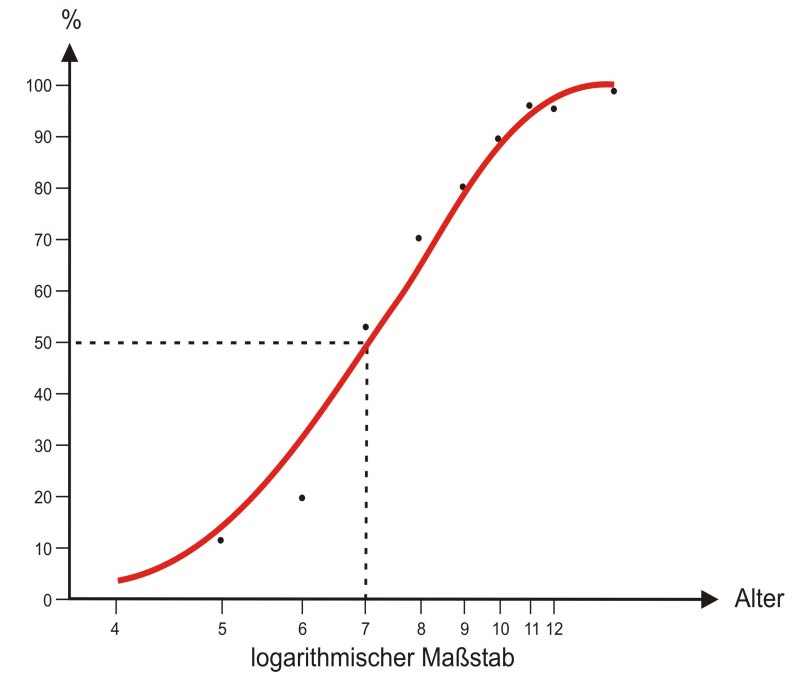

Abbildung 1.2: Lösungswahrscheinlichkeit einer Binet-Aufgabe in Abhängigkeit vom Lebensalter (logarithmischer Maßstab auf der Abszisse;nach Amelang & Bartussek, 1997).

So kamen Binet und Simon zu einem Maß, das sie Intelligenzalter nannten (IA) und zu dem der Abstand jedes Kindes bestimmt werden konnte (s. dazu auch Lehreinheit Intelligenz). Dieses Intelligenzalter musste über alle Probanden hinweg dem Lebensalter entsprechen.

Bestimmung des Intelligenzalters nach Binet

Um die Bestimmung des Intelligenzalters genauer nachvollziehen zu können, kann ein hypothetisches Lösungsmuster eines Kindes, wie in Tabelle 1.1 dargestellt, betrachtet werden. Kindern wurden in jeder Altersserie immer 5 Aufgaben vorgelegt. Ein Beispiel gibt      Tabelle 1.1

Dieses Kind von 7 Jahren löst beispielsweise alle Aufgaben für 6- und 7-Jährige, dazu 3 Aufgaben für 8- und 9-Jährige sowie zwei Aufgaben für 10-Jährige. Für die Berechnung des Intelligenzalters geht man nun von der Altersklasse aus, bis zu der das Kind alle Aufgaben löste (7). Dies ist das Grundalter für das Intelligenzalter, das in Monatsäquivalenten angegeben wird (7x12). Für jede weitere gelöste Aufgabe (8) wird nun 1/5 (da 5 Aufgaben einer Altersserie) jeden Jahres in Monatsäquivalenten hinzugezählt (8x12/5), sodass in diesem Fall ein Intelligenzalter von 103 Monaten entsteht, wobei üblicherweise noch mal 5/2 Aufgaben in Monatseinheiten hinzugezählt werden.

Die Tests, die nach altersbezogenen Schwierigkeitsstufen geordnet waren, waren jedoch der Kritik ausgesetzt, da die Differenzen nicht nach dem tatsächlichen Alter gewichtet waren. So konnte eine Differenz von zwei IA-Einheiten bei einem 10-jährigen Kind unauffällig sein, bei einem 4-jährigen jedoch auf Schwachsinn hindeuten (vgl. dazu Amelang & Barussek, 1997). Diesem Umstand versuchte William Stern (1911) mit der Berechnung eines Intelligenzquotienten (IQ) zu begegnen, der das IA in Bezug zum Lebensalter (LA) setzte. Dieser berechnete sich wie folgt: IQ = IA/LAx100. (Zu heutigen Berechnungen der Intelligenz s. Lehreinheit „Intelligenz“)

William Stern hat sich jedoch nicht nur mit diesem Vorschlag zur Berechnung eines Intelligenzquotienten, sondern vor allem durch die Publikation „Über die Psychologie der individuellen Differenzen – Idee zu einer Differentiellen Psychologie“ (s. Stern, 1911) große Verdienste zur Etablierung der Differentiellen Psychologie erworben. So thematisiert er u.a. methodische Zugänge wie die Variations- und Korrelationsforschung und die Psychografie und Komparationsforschung, die bereits wesentliche Probleme der Differentiellen Psychologie thematisieren. Abbildung 1.3 gibt einen Überblick über die methodischen Zugänge.

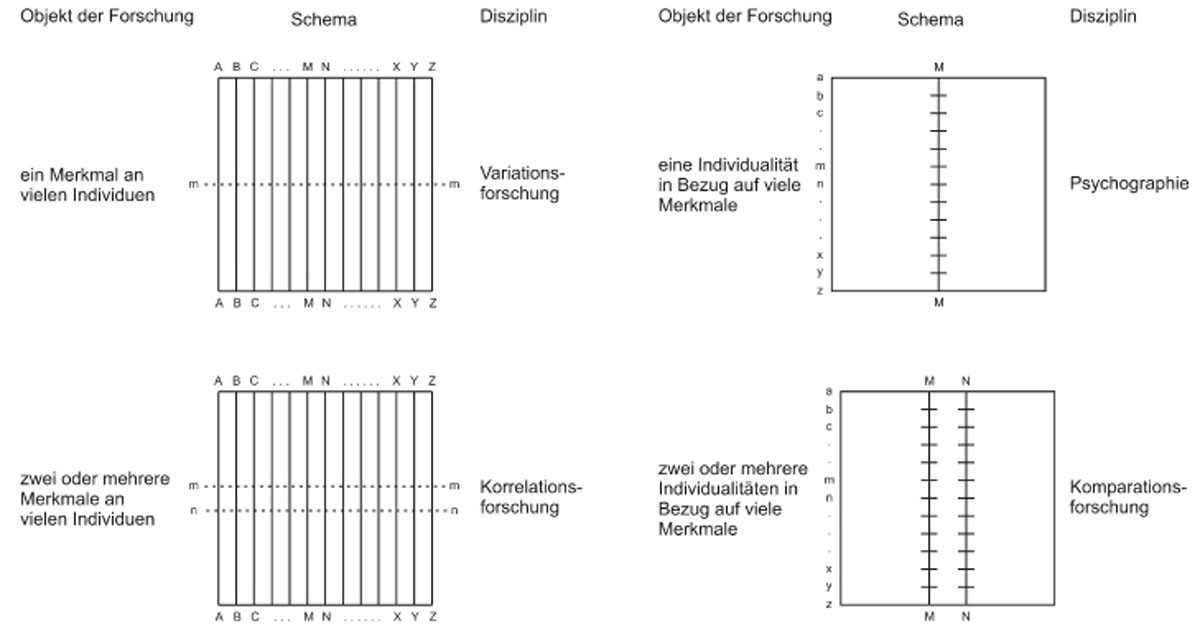
Abbildung 1.3: Methodische Zugänge zur Differentiellen Psychologie (modifiziert nach Stern 1921).

In Abbildung 1.3 bezeichnen die Großbuchstaben Individuen (Personen) und die kleinen Buchstaben einzelne Merkmale (wie z.B. Intelligenz). Die einzelnen Techniken können danach wie folgt charakterisiert werden:

• Die Variationsforschung betrachtet ein Merkmal (m) bei vielen Individuen (A, B, C, …).
• Die Korrelationsforschung betrachtet zwei oder mehr Merkmale (m, n, ...) an vielen Individuen (A, B, C, …) und stellt die Frage, welches Merkmal geht mit welchem anderen Merkmal einher.
• Die Psychografie, einer der ältesten Zugänge zu Fragen der Differentiellen Psychologie, betrachtet viele Merkmale (a, b, c,…) an einem Individuum (M).
• Die Komparationsforschung betrachtet viele Merkmale (a, b, c,…) an zwei oder mehr Individuen (M, N, …).

Diese Art der Betrachtung von Individuen und Merkmalen kann zur Beantwortung vieler der eingangs erwähnten Fragen beitragen. Es fehlt jedoch die dritte Ebene, die Veränderung der Situation (z.B. die Frage nach der Beeinflussbarkeit durch Trainings oder Interventionen). Diesem Umstand hat Cattell (1957) Rechnung getragen, indem er neben Individuen (Personen) und Merkmalen (die er Variablen nennt) auch Situationen in einem dreidimensionalen Modell, einem Datenquader, kombiniert hat. Er kommt dadurch zu unterschiedlichen Korrelationstechniken, die in Tabelle 1.2 erläutert sind.