Demokurs: Approach to the Basics of Calculus - DEUTSCH
Folgen-Grundlagen

|
|
Dieser Abschnitt behandelt wichtigste Definitionen zum Begriff der Folge. Dabei wird der Begriff zunächst allgemein gefasst, dann aber auf reelle Zahlenfolgen eingeschränkt. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Definition 1 (Folge). M sei eine nichtleere Menge. Eine Folge ist eine Abbildung
Gelegentlich spricht man auch von einer Folge in M.
Definition 2 (Folgenglied und Index): Für eine Folge schreibt man (a1, a2, a3, …) oder kürzer (an)n statt f(n). Die Zahlen a1,a2,a3,… ∈ M heißen die Glieder der Folge oder Folgenglieder. Wegen der Zuordnung
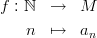
|
Zufallsfolge von Farbquadraten. Es wird jeweils nur ein Folgenglied angezeigt.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Beispiel: Folge der natürlichen Zahlen 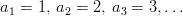 Bei dieser speziellen Folge ist jedes Folgenglied gleich seinem Index. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
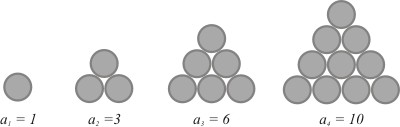
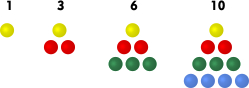
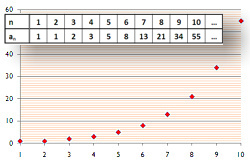
Beispiel: Folge der Dreieckszahlen
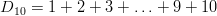
Schreibweise und Definition (Summenfolge):
Ist (an)n,an : ℕ → M eine Folge mit Folgegliedern an, so schreibt man die Summe
Das Zeichen ∑ heißt Summenzeichen, der Summenindex k läuft hier von 1 bis n. Man nennt Folgen, deren Folgeglieder durch Summation vorangegangender Folgeglieder entstehen, auch Summenfolgen.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Beispiel: Folge der Quadratzahlen Interessant: Die Summe zweier aufeinanderfolgender Dreieckszahlen ist eine Quadratzahl. So ist etwa 3 + 1 = 4 und 6 + 3 = 9. Allgemein gilt der Zusammenhang
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
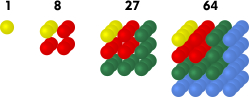
Beispiel: Folge der Kubikzahlen
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Wählt man in Definition 1 die Menge M = ℝ, so erhält man:
Definition 2 (Zahlenfolge) Eine reelle Zahlenfolge ist eine Abbildung
Streicht man aus einer Folge beliebig viele Folgeglieder heraus, behält die Reihenfolge aber bei, so erhält man eine sogenannte Teilfolge. Mathematisch definiert lautet dies so: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Definition 4 (Teilfolge): Für eine Folge (an)n und eine streng monoton wachsende Abbildung
nennt man die Komposition2
eine Teilfolge von (an)n. |
H. Böhm: Relief 6 Punkte ... (1959)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Beispiel: Es sei (qn)n mit qn := n2 die Folge der Quadratzahlen, also
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Beispiel: Es sei die Folge (an)n mit an :=
und es sei (bn)n ihre 1. Differenzenfolge. Dann gilt:
und ein Folgenglied von (bn)n hat die allgemeine Form 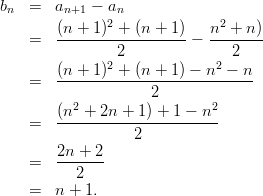
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Aufgabe: Stellen Sie die Folge der Quadratzahlen auf mindestens drei verschiedene Weisen dar. Aufgabe: Es sei (πn)n die Folge der Nachkommastellen der Kreiszahl π. Ist die endliche Folge (1,4,1,5,9,2) eine Teilfolge von (πn)n? Begründung!
|


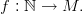


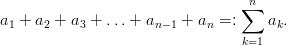
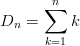
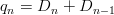

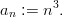
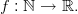
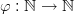
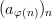

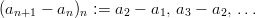
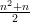 gegeben, also
gegeben, also 