Grundlagen der anwendungsbezogenen Hochschulmathematik
6. Integralrechnung
6.7. Anwendungen

In diesem Kapitel stellen wir Beispiele vor, bei denen die Integration ein wesentlicher Bestandteil der Berechnung ist.

Beispiel 1 (Beschleunigung)
Die Ableitung einer Strecke \(s=s(t)\) nach der Zeit ergibt die Geschwindigkeit: \(v(t)=\frac{\mathrm{d}}{\mathrm{d}t}s(t)\). Die Ableitung der Geschwindigkeit wiederum ergibt die Beschleunigung: \(a(t)=\frac{\mathrm{d}}{\mathrm{d}t}v(t)=\frac{\mathrm{d^2}}{\mathrm{d}t^2}s(t)\).
Umgekehrt bedeutet das, dass sich Geschwindigkeit und Weg durch ein- bzw. zweimalige Integration der Beschleunigung ergeben:
\[v = \int a(t)\, \mathrm d t, \quad s = \int v(t)\, \mathrm d t\].
Durch die unten angegebenen Rechnungen ergeben sich die aus der Physik bekannten Formeln für Geschwindigkeit und Weg in Abhängigkeit von einer konstanten Beschleunigung. Konstante Beschleunigung bedeutet, dass die Funktion für die Beschleunigung konstant ist, d.h. \(a(t)\equiv \mbox{const}\). Im Folgenden wird also mit der Konstanten \(a\) gerechnet.
Für die Geschwindigkeit gilt:
\[v = \int a \mathrm d t = at + C_1 \].
Die Integrationskonstante wird dabei aus dem Anfangswert \(v(0) = v_0\) berechnet, es folgt
\[v(t) = a\cdot t + v_0\].
Für den Weg ergibt sich damit:
\begin{equation} s(t) = \int v(t)\, \mathrm d t = \int (a\cdot t + v_0)\, \mathrm d t = \frac{1}{2} a\cdot t^2 + v_0\cdot t + C_2.\end{equation}
In diesem Fall ist die Integrationskonstante der Anfangsort \(s(0) = s_0\) und somit gilt:
\[s(t) = \frac{1}{2} a\cdot t^2 + v_0 \cdot t + s_0.\]

Beispiel 2 (Effektivwert)
Die momentane Spannung in einem Wechselstromkeis sei durch
\[u(t) = u_m \cos(\omega t) \]
und die momentane Stromstärke sei durch \[i(t)= i_m \cos(\omega t + \phi).\]
Die momentane Leistung beim Wechselstrom ist gegeben durch
\[u(t)i(t) = u_m \cos(\omega t) \cdot i_m \cos(\omega t + \phi).\]
Die Wirkleistung ist definiert als
\[\bar{P_0} = \frac1T \int_0^T u(t)i(t)\mathrm d t = \frac1T \int_0^T u_m \cos(\omega t) \cdot i_m \cos(\omega t + \phi)\mathrm d t.\]
Es ist also das Integral \( \int_0^T u_m \cos(\omega t) \cdot i_m \cos(\omega t + \phi)\mathrm d t\) zu berechnen. Hierbei helfen uns die Addtionstheoreme:
\[2\cos\left(\frac{x+y}2\right) \cdot \cos\left(\frac{x-y}2\right) = \cos(x) + \cos(y).\]
Aus \( \frac{x+y}2=\omega t + \phi\) und \( \frac{x-y}2=\omega t\) erhalten wir
\[x=2\omega t + \phi \qquad \mbox{und} \qquad y = \phi t\]
Damit erhalten wir
\[u(t)i(t) = \frac{u_m \cdot i_m}{2}\left(\cos(\phi) + \cos(2\omega t + \phi)\right).\]
Mit \(U = \frac{u_m}{\sqrt{2}}\) und \(I = \frac{i_m}{\sqrt{2}}\)
\begin{eqnarray} \bar{P_0} & = & \frac{U\cdot I}T \int_0^T \cos(\phi) + \cos(2\omega t + \phi)\mathrm d t\\& = & U I \cos(\phi) \end{eqnarray}
Dieses Beispiel orientiert sich an dem Beispiel von Burg, Haf, Wille: Höhere Mathematik für Ingenieure, Band I: Analysis, 8. Auflage, Teubner Verlag 2008, Kapitel 4.4, S. 349

Beispiel 3 (Wasserdruck auf eine Seitenwand)
Wir betrachten ein Wasserbecken mit einer Seitenwand in Form einer Ellipse. Die Wand kann durch \[\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\]
beschrieben werden. Wir stellen uns vor, dass diese Seitenwand in infinitesimal schmale Streifen der Höhe \(\mathrm{d}y\) und der Breite \(2x\) geschnitten wurde. Der Flächeninhalt eines Streifens ist dann \[\mathrm{d}f = 2x\,\mathrm{dy}.\]
Der Wasserdruck \(\mathrm{d}P\) auf diesem Streifen hängt von der Höhe des Wassers darüber ab; das Wasser gehe bis zur \(x\)-Achse. Damit ist der Druck gegeben durch
\[\mathrm{d}P = 2x\mathrm{d}y \cdot y \cdot \gamma.\]
Um den Gesamtdruck \(P\), der auf die Seitenwand wirkt, zu berechnen, müssen wir über die gesamte Wasserhöhe integrieren. Das heist also \[P = \int_{y=0}^{y=b} 2x \cdot y \cdot \gamma\, \mathrm{d}y.\]
Nun hängt der Integrand aber von \(x\) ab. \(x\) können wir aber durch \(y\) ausdrücken, denn es gilt:
\[ x = a\sqrt{1-\frac{y^2}{b^2}}=\frac{a}{b}\sqrt{b^2-y^2}.\]
Dies führt nun auf \[P = \int_{y=0}^{y=b} 2x \cdot y \cdot \gamma\, \mathrm{d}y=\int_{y=0}^{y=b} 2\frac{a}{b}\sqrt{b^2-y^2} \cdot y \cdot \gamma \,\mathrm{d}y.\]
Das Integral kann nun mit Hilfe der Substitution \(z = b^2-y^2\) und \(\mathrm{d}z = -2y\mathrm{d}y\) gelöst werden. An den Rändern müssen wir aber bei der Substitution aufpassen: \(z(0) = b^2\) and \(z(b) = 0\).
Mit diesen Überlegungen erhalten wir nun:
\begin{eqnarray} P & = & \int_{y=0}^{y=b} 2\frac{a}{b}\sqrt{b^2-y^2} \cdot y \cdot \gamma\, \mathrm{d}y\\& = & \gamma\int_{z=b^2}^{z=0} -\frac{a}{b}\sqrt{z} \mathrm{d}z \\ & = & \gamma\frac{a}{b} \left[-\frac23z^{\frac32}\right]_{z=b^2}^{z=0}\\& = & \gamma\frac{a}{b} \left[-0+\frac23(b^2)^{\frac32}\right]=\frac23 \gamma a b^2.\end{eqnarray}.
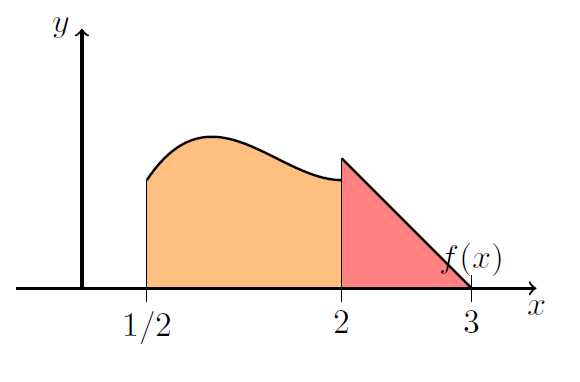

Geometrische Anwendungen
Beispiel 4 (Flächeninhalte)
Die bekannteste Anwendung ist die Interpretation des Integrals als Fläche zwischen einer Funktion und der \(x\)-Achse.
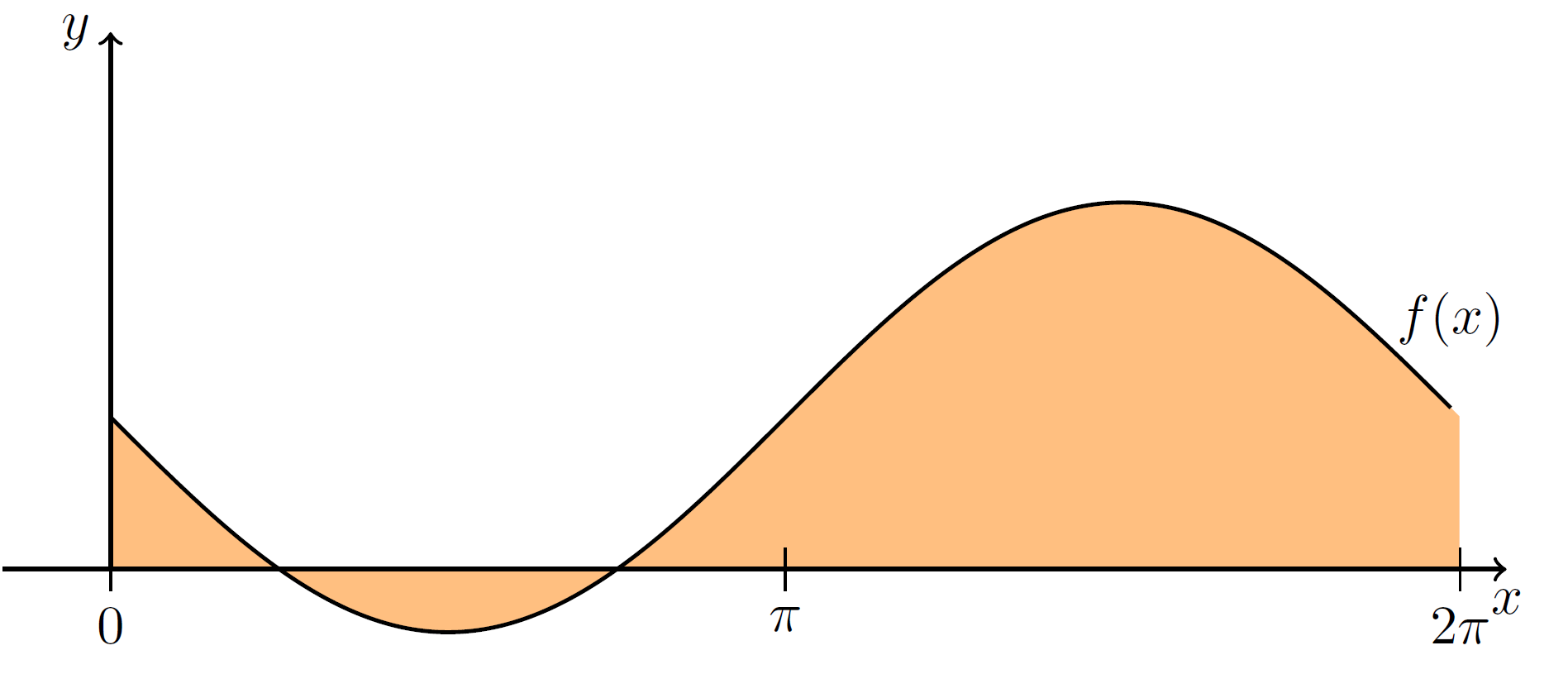
Der Flächeninhalt ist gegeben durch \(A = \int_a^b |f(x)|\,\mathrm{d}x\). Im Bild ist die \(f(x) = -\sin(x)+\frac1{\sqrt{2}}\) dargestellt und der Flächeninhalt kann berechnet werden durch
\[A = \int_0^{2\pi} |f(x)|\,\mathrm{d}x = \int_{0}^{\frac{\pi}4}-\sin(x)+\frac1{\sqrt{2}}\,\mathrm{d}x +\]
\[+\int_{\frac{\pi}4}^{\frac{3}4\pi}\sin(x)-\frac1{\sqrt{2}}\,\mathrm{d}x\int_{\frac{3}4\pi}^{2\pi}-\sin(x)+\frac1{\sqrt{2}}\,\mathrm{d}x=\sqrt{2}\pi.\]
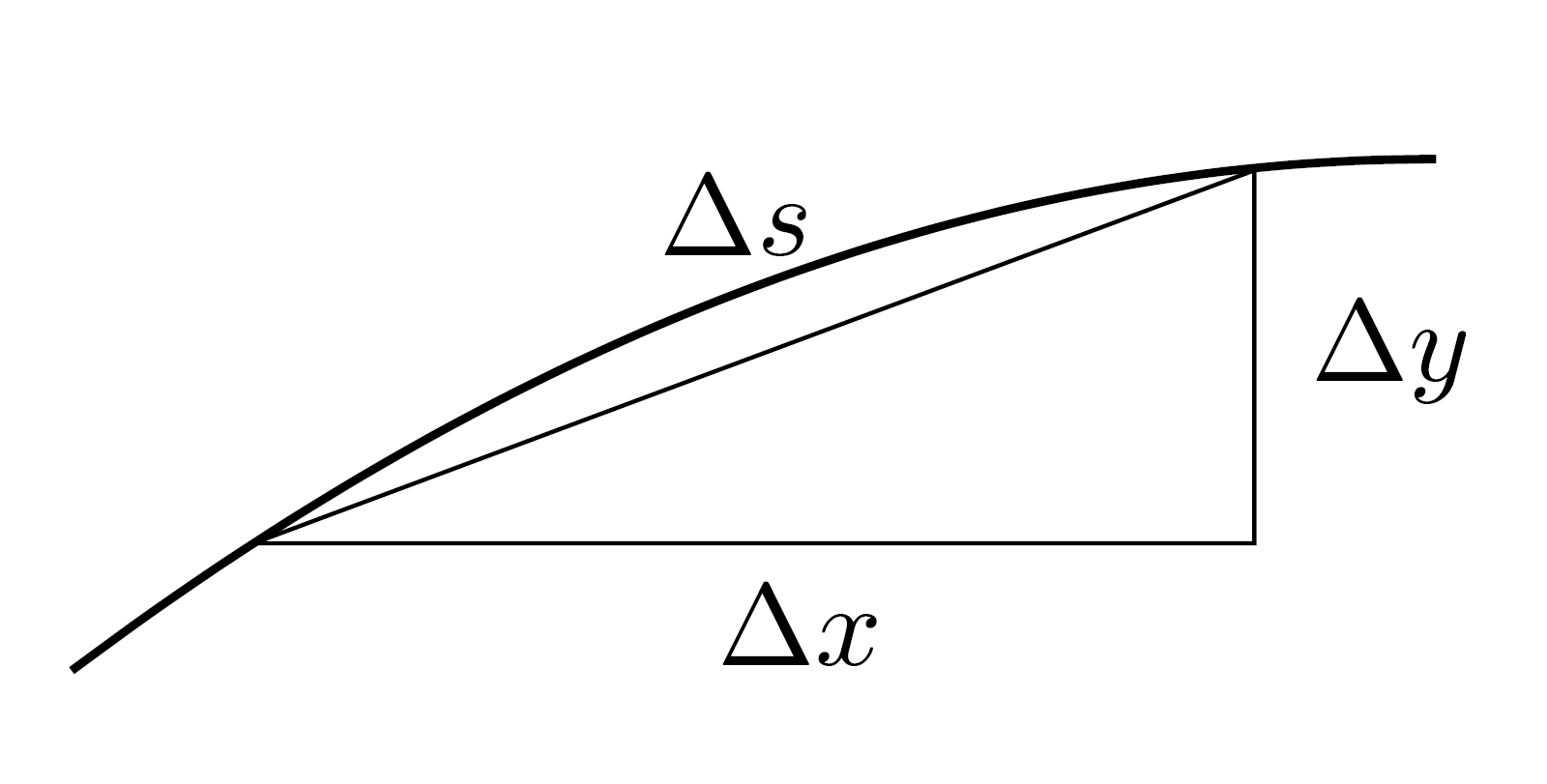
Beispiel 5 (Länge eines Funktionsgraphen)
Die zugrundeliegende Idee ist ganz interessant. Ein infinitesimal kleines Stück des Graphen besitzt die Länge\[\Delta s \approx \sqrt{(\Delta x)^2+(\Delta y)^2}=\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x\approx \sqrt{1+f'(x)^2}\Delta x.\]
Wenn wir nun über das Intervall \((a,b)\) integrieren, erhalten wir
\[l = \int_a^b \sqrt{1+f'(x)^2} \,\mathrm{d}x.\]
Damit erhalten wir für die Länge des Graphen der Funktion \(g(x) = \cosh(x)\) über \([-1,1]\)
\[ l = \int_{-1}^{1} \sqrt{1+\sinh(x)^2} \,\mathrm{d}x = \int_{-1}^{1} \cosh(x) \,\mathrm{d}x = 2\sinh(1).\]
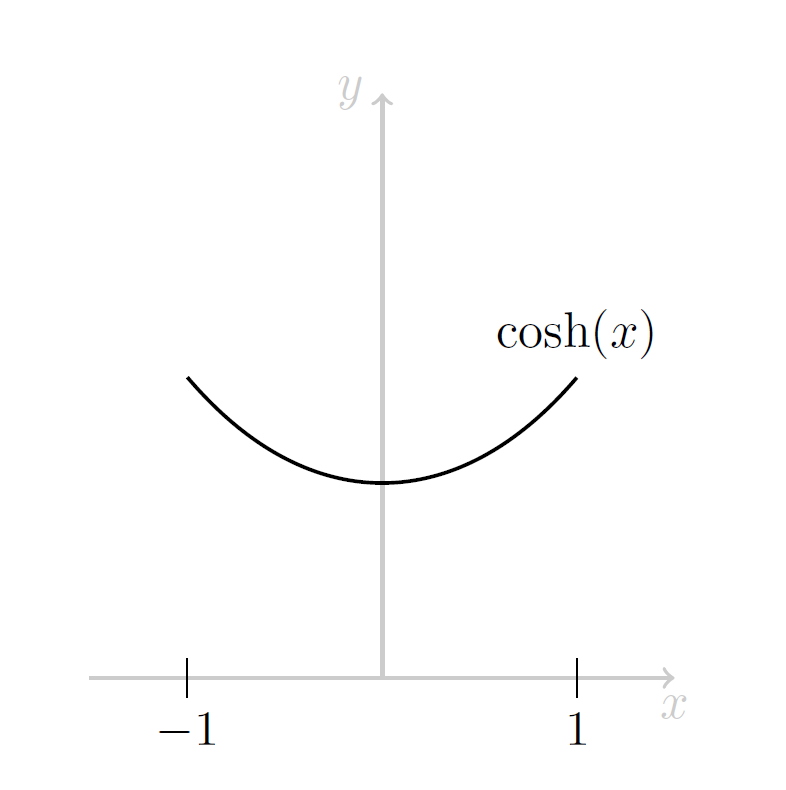
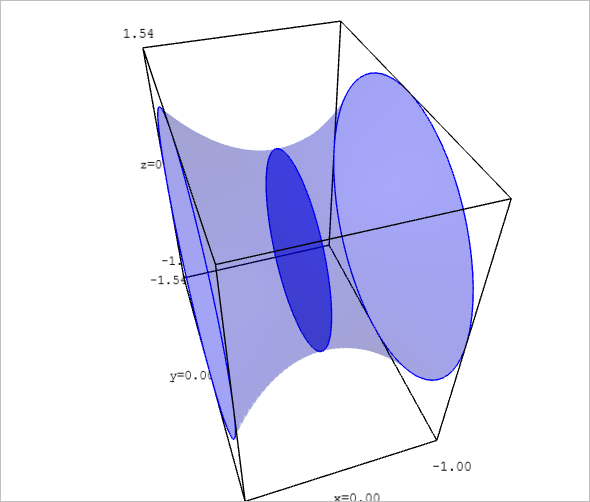
Beispiel 6 (Flächeninhalt einer Rotationsfläche)
Wieder betrachten wir eine Funktion \(y=f(x)\) auf dem Intervall \([a,b]\). Diesmal wird die Funktion um die \(x\)-Achse rotiert, d.h. die Funktion \(f(x) = \cosh(x)\) auf \([-1,1]\).
Für ein beliebiges \(x\) aus diesem Interval sehen wir infinitesimal dünne Kreise mit der Bogenlänge \(2\pi |f(x)|\) und der Breite \(\sqrt{1+f'(x)^2}\Delta x\). Auf diese Weise erhalten wir den Flächeninhalt dieses Kreises
\[2\pi |f(x)|\cdot\sqrt{1+f'(x)^2}\Delta x.\]
Durch Integration über das Intervall \([a,b]\) erhalten wir den Flächeninhalt
\[A = 2\pi\int_a^b |f(x)|\cdot\sqrt{1+f'(x)^2}\,\mathrm{d}x. \]
In unserem Beispiel erhalten wir
\[ A = 2\pi \int_{-1}^{1} \cosh(x)\sqrt{1+\sinh(x)^2}\,\mathrm{x} = 2\pi \int_{-1}^{1} \cosh(x)^2\,\mathrm{x}=2 \pi (1 + \sinh(1) \cosh(1)).\]
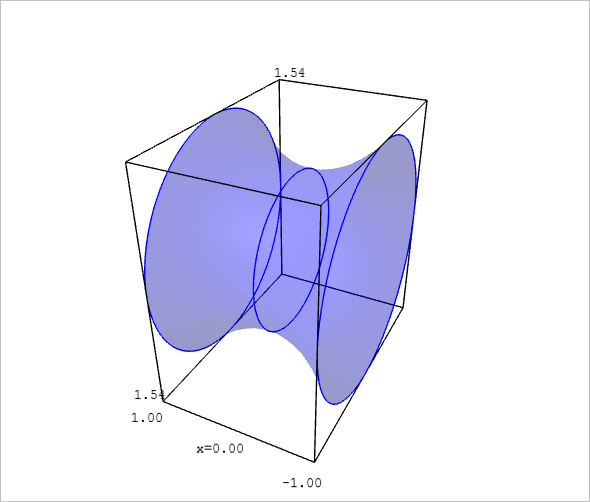
Beispiel 7 (Volumen eines Rotationskörpers)
Wir erweitern nochmal die Idee von oben. An jedem Punkt \(x\) überdeckt der Kreis die Fläche \(A(x) = \pi f(x)^2\). Durch Integration von \(a\) nach \(b\) erhalten wir das Volumen \[ V = \int_a^b A(x) \,\mathrm{d} x = \pi \int_a^b f(x)^2\,\mathrm{d} x.\]
In unserem Beispiel führt dies auf folgendes:
\[ V = \int_{-1}^{1} A(x) \,\mathrm{d} x = \pi \int_{-1}^{1} f(x)^2\,\mathrm{d} x =\pi \int_{-1}^{1} \cosh(x)^2\,\mathrm{d} x = \pi (1 + \sinh(1) \cosh(1)).\]