Grundlagen der anwendungsbezogenen Hochschulmathematik
| Website: | WueCampus |
| Kurs: | Demo-FAQ |
| Buch: | Grundlagen der anwendungsbezogenen Hochschulmathematik |
| Gedruckt von: | مستخدم ضيف |
| Datum: | Freitag, 5. Dezember 2025, 10:43 |
1. Zahlen und Terme


Das Kapitel Zahlen und Terme umfasst:

- Mengendarstellungen und -operationen (Wiederholung!)
- Komplexe Zahlen
- Elementare algebraische Regeln (Wiederholung!)
- Terme und erste Gleichungen
- Lineare und Quadratische Gleichungen
- Exponentielle und logarithmische Gleichungen
- Trigonometrische Gleichungen
- Aufgaben

1.1. Mengen und Zahlen


Mengendarstellungen und -operationen
Mengen begegnen uns häufig im Alltag, auch wenn wir diese nicht so bewusst wahrnehmen. Auf vielen Ausschreibungen findet man die Bezeichnung m, w, d. Dies lässt sich als Menge der Geschlechteridentitäten auffassen.
Definition 1 (Menge)
Unter einer Menge M versteht man die Zusammenfassung von bestimmten, wohlunterschiedenen Objekten zu einem Ganzen. Die Objekte, die zu einer Menge zusammengefasst werden, heißen Elemente dieser Menge.
Es gibt endliche und unendliche Mengen. Die Geschlechteridenditäten von oben sind offensichtlich eine endliche Menge. Die Elemente kleiner endlicher Mengen werden wie folgt notiert:
\(G=\{m, w, d\}\)
Um aufzuzeigen, dass ein Element in einer Menge liegt schreibt man:
\(m \in M\) falls \(m\) ein Element von \(M\) ist.
Mithilfe dieser Notation wollen wir im Folgenden die aus der Schule bekannten Zahlenmengen betrachten.
Die aus dem Alltag bekannten Zahlen 1, 2, 3, ... stellen auch eine Menge dar. Diese bezeichnet man als natürliche Zahlen und fässt sie mit dem Mengensymbol \( \mathbb{N} \) zusammen. Hierbei handelt es sich um eine unendliche Menge. Möchte man diese Menge um das Element 0 erweitern, schreibt man \( \mathbb{N}_0 \).
Die ganzen Zahlen \( \mathbb{Z} \) umfassen zusätzlich auch die negativen Zahlen.
Durch Betrachtung von Quotienten beliebiger ganzer Zahlen erhält man die rationalen Zahlen \( \mathbb{Q} \), die manchmal auch in der Alltagssprache Bruchzahlen genannt werden. Jede Diese können sowohl als Bruch als auch als periodische Dezimalzahlen dargestellt werden (Hinweis: \( \frac{1}{2} = 0,5\overline{0} \) und damit periodisch).
Es gibt allerdings auch unendlich, nicht-periodische Dezimalzahlen wie \( \sqrt2 \) oder \( \pi \). Diese nennt man irrational. Die Gesamtheit aus rationalen und irrationalen Zahlen bildet die reellen Zahlen \( \mathbb{R} \) - Exkurs: Beweis der Irrationalität von \( \sqrt{2} \).
Diese können wiederum zu den komplexen Zahlen \( \mathbb{C} \) erweitert werden (s. folgende Kapitel).
Bisher haben wir vom Erweitern von Mengen besprochen, entsprechend lässt sich auch der Blick zurück werfen. Hierfür definieren wir die sogenannte Teilmenge:


Definition 2 (Teilmenge)
Eine Menge T heißt Teilmenge einer Menge M, wenn jedes Element von T auch ein Element von M ist.
\( T \subseteq M \Leftrightarrow \forall t :(t \in T \Rightarrow t \in M) \)
Hinweis: Das Zeichen \( \forall \) bedeutet "Für alle" und die Doppelpunkte \( : \) (manchmal auch ein Querstrich \( | \)) "es gilt".
Um deutlich zu machen, dass eine Menge eine 'echte' Teilmenge T einer Menge ist, d.h. es existiert ein Element \(m \in M\) für das gilt \(m \notin T\) schreiben wir \( \subset \) oder \(\subsetneq\)
Für die oben betrachteten Zahlenmengen gilt dabei \( \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} \).
Man kann mit Mengen auch in gewisser Weise "rechnen". So bezeichnet \( \bigcap \) den Schnitt und \( \bigcup \) die Vereinigung zweier Mengen. Sind bspw. \( U \) bzw. \( G \) die Menge der ungeraden bzw. geraden Zahlen, so ist
\( U \bigcap G = \emptyset \) ("leere Menge")
\( U \bigcup G = \mathbb{Z} \)

Teilbarkeit
Definition 3 (Teilbarkeit)
Eine Zahl \( n \) heißt teilbar durch \( t \), genau dann wenn es eine natürliche Zahl \( m \) gibt mit \( m \cdot t = n \).
Beispielsweise ist jede natürliche Zahl mit 0 an der letzten Stelle durch 10 teilbar.
Warum wir uns dafür interessieren: Im Kapitel 1.3 werden wir uns mit Brüchen auseinandersetzen, wobei wir diese beim Kürzen auf Teilbarkeit hin überprüfen werden. Zunächst wollen wir deshalb nur natürliche Zahlen auf Teilbarkeit überprüfen. Damit Betrachten wir gleichzeitig auch ganze Zahlen auf Teilbarkeit, da "neue" Teiler dabei lediglich ein negatives Vorzeichen erhalten können.
Teilermenge:
Die Teilermenge ist die Menge aller Teiler einer Zahl. Man schreibt \(T(x)\) für die Teilermenge. Die Mächtigkeit dieser Menge entspricht der Anzahl der Teiler und wird angegeben durch \( \vert T(x) \vert \).
Beispiel: \(T(15)={1, 3, 5, 15}\)

Übung:
| Zahl x | T(x) | \( \vert T(x) \vert \) |
| 3 | ||
| 4 | ||
| 30 | ||
| 1001 |

1.2. Komplexe Zahlen


Komplexe Zahlen
Betrachten wir die Gleichung \( x²+1=0 \) in \( \mathbb{R} \), so löst kein \( x \in \mathbb{R} \) die Gleichung. Wir erweitern deshalb \( \mathbb{R} \) zu den komplexen Zahlen \( \mathbb{C} \).
Die Menge der komplexen Zahlen, oft bezeichnet mit \( \mathbb{C} \), ist definiert als ein Tupel \( z=(x,y) \), wobei \( x,y \in \mathbb{R} \), mit den mathematischen Operationen Addition (Summe) und Multiplikation (Produkt) definiert ist als:\[ (\textrm{Summe}) \qquad z_1+z_2 = (x_1,y_1)+(x_2,y_2) = (x_1+x_2 \, , \, y_1+y_2) \] \[ (\textrm{Produkt}) \qquad z_1z_2 = (x_1,y_1)(x_2,y_2) = (x_1x_2-y_1y_2 \, , \, x_1y_2+x_2y_1) \]
Geometrisch können die komplexen Zahlen als Punkte oder Vektoren einer zweidimensionalen Ebene (komplexe Ebene) verstanden werden, wobei die horizontale Achse die reelle Achse und die vertikale Achse die imaginäre Achse ist.
Für eine komplexe Zahl \( z=(x,y)\), \(x\) ist der Realteil und \(y\) der Imaginärteil. Sie werden als \( \textrm{Re }z \) und \( \textrm{Im }z \) bezeichnet. Wenn \( \textrm{Re }z =0 \), dann ist \( z \) rein imaginär, und wenn \( \textrm{Im }z =0 \), dann ist \( z \) reell.
Die Menge der komplexen Zahlen ist eine natürliche Erweiterung der Menge der reellen Zahlen: wenn die reelle Zahl \( x \) mit \( (x,0) \) bezeichnet wird (eine komplexen Zahl, deren Imaginärteil Null ist), erscheinen die Summe und das Produkt wie oben definiert gleich der Summe und dem Produkt zweier reeller Zahlen zu sein. Ähnlich zu den reellen Zahlen sind Subtraktion und Division komplexer Zahlen als inverse Operationen der Addition und Multiplikation definiert. Die Summe und das Produkt zwischen den komplexen Zahlen haben die üblichen Eigenschaften, die bereits von den reellen Zahlen bekannt sind wie Kommutativität, Assoziativität und Distributivität. Man rechnet leicht nach, dass dies weiterhin gilt
Rein imaginäre Zahlen \( (0,1) \) werden mit \( i \) bezeichnet (imaginäre Einheit). Mit dieser Notation kann eine komplexe Zahl \( z=(x,y) \) geschrieben werden als
\[ z=x+iy \]
welches die übliche Notation ist und umgänglicher beim Rechnen ist als die Notation mit \( (x,y) \) .
Mit Anwendung der Definition des Produkts ist es leicht zu sehen, dass die Gleichung \[ i^2 = -1 \] valide ist. Dies wird oft als die wichtigste Gleichung in der komplexen Analysis angesehen.
Beachte: Basierend auf der ersten Gleichung ist die Wurzel einer negativen Zahl manchmal als \( \sqrt{-1}=i \) und \( \sqrt{-a} = i\sqrt{a} \) definiert, aber diese Gleichungen können nicht im Allgemeinen als Definitionen betrachtet werden: Sie sind fehlerhaft, auch wenn es Situationen gibt, in denen sie in Rechnungen angewandt werden ohne falsche Ergebnisse zu liefern.

Konjugation, Betrag und Argument
Das komplex konjugierte \( \overline{z} \) einer komplexen Zahl \( z=x+iy \) ist definiert als \[ \overline{z}=x-iy. \]
Graphisch gesehen enstpricht die Konjugation somit der Spiegelung eines Punktes an der reellen Achse. Bspw. ist \( \overline{i} = -i \), d.h. der Punkt \( (0,1) \) wird auf den Punkt \( (0,-1) \) gespiegelt.
Der Absolutwert oder Betrag einer komplexen Zahl \( z=x+iy \) ist \[ |z| = \sqrt{x^2+y^2}. \] Graphisch ist dies der (euklidische) Abstand des Punktes zum Nullpunkt.
Das Argument von \( z \), bezeichnet als \( \textrm{arg }z \), ist der gerichtete Winkel zwischen der positiven \( x \)-Achse und dem Ortsvektor des Punktes \( z \) in der komplexen Ebene. Das Argument kann positiv oder negativ sein und kann jegliche reellen Werte annehmen. Wenn \( z=x+iy \) und \( \phi=\textrm{arg z} \), dann ist mit der Definition des Tangens \[ \tan \phi = \frac{y}{x}. \] Das Argument ist nicht eindeutig, aufgrund der Periodizität der trigonometrischen Funktionen, aber Argumente zwischen \( 0 \) und \( 2\pi \) oder zwischen \( -\pi \) und \( \pi \) werden am häufigsten benutzt. Wenn Winkel zwischen \( -\pi \) und \( \pi \) benutzt werden, dann ist das Argument der komplexen Zahl \( z=x+iy \) mit positivem Realteil \( \textrm{arg} z = \arctan\frac{y}{x} \),und wenn der Realteil negativ ist, dann \( \textrm{arg} z = \pi + \arctan\frac{y}{x} \).
Die Polarform einer komplexen Zahl basiert auf ihrem Betrag, ihrem Argumen und den Definitionen von Sinus und Cosiunst: \[ z=|z|(\cos\phi + i\sin\phi). \] Durch Anwenden der Euler'schen Formel \[ e^{ix} = \cos x +i\sin x \] kann die Polarform auch in eine exponentielle Form gebracht werden \[ z=|z|e^{i\phi}. \]
Die Eulersche Formel kann bewiesen werden, wenn wir zuerst die Potenzreihen-Darstellung der Exponentialfunktion \[ e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \] für komplexe Exponenten erweitern, und dann die Darstellung der Potenzreihen für Sinus und Cosinus anwenden.
Beispiel 1.
Wenn \( z=-2+i2\sqrt{3} \), dann ist \( |z|=\sqrt{(-2)^2 +(2\sqrt{3})^2} = 4 \) und das Argument ist der Winkel \( \phi \), so dass \( \tan \phi = \frac{2\sqrt{3}}{-2} = -\sqrt{3}\). Da der Realteil negativ ist, kann das Argument als Winkel \( \pi + \arctan(-\sqrt{3}) = \pi + (-\frac{\pi}{3}) = \frac{2\pi}{3} \) ausgedrückt werden. Somit ist die exponentielle Form \( z = 4 e^{i \frac{2\pi}{3}} \).
Durch Anwenden der exponentiellen Form ist leicht zu sehen, dass \[ z^n = |z|^n e^{in\phi} = |z|^n(\cos n\phi + i\sin n\phi). \] Merke auch, dass wegen der Periodizität von Sinus und Cosinus, wenn \( n \) ganzzahlig ist, dann
\[ |z|e^{i(\phi+n2\pi)} = |z|e^{i\phi}. \]

1.3. Elementare algebraische Regeln


Elementare algebraische Regeln
Wir wollen zunächst die wichtigsten algebraischen Begriffe und Rechenregeln wiederholen. Die Grundlegenden Rechenoperationen sind Addition und Subtraktion sowie Multiplikation und Division. Betrachtet man die Verknüpfung dieser Operationen müssen wir zunächst ein paar Grundlegende Regeln wiederholen, damit man nicht auf das häufig im Netz verbreitete Problem stößt, dass die Lösung von \(6:2(1+2)=1\) falsch ist.
Potenzen und Rechenregeln
Für Produkte aus gleichen Faktoren \(a \in \mathbb{Q} \) wird die folgende Kurzschreibweise verwendet: \( \underbrace{a \cdot \dots \cdot a}_{n \textrm{ mal}} (n \in \mathbb{N}) \) mit n Faktoren.
Insbesondere gilt \(a^1=a\)
Wir bezeichnen n als Exponenten und a als die Basis.
Wir definieren:
Definition 1 (Potenzen mit ganzzahligen Exponenten)
\(a^0=0\) für alle \(a \in \mathbb{Q} \)
und
\( a^{-n}=\frac{1}{n}\) für alle \(a \in \mathbb{Q} \setminus \{0\} \) und \( n \in \mathbb{N}\)
Bruchrechnen mit Bruchtermen
Ein Bruch \( \frac{a}{b} \) besteht aus dem Zähler \( a \) und dem Nenner \( b \), die durch den Bruchstrich voneinander getrennt sind. Inhaltlich kann man einen Bruch als Division \( a:b \) verstehen.Multiplikationsregel für Brüche
Brüche werden multipliziert, indem man die Zähler miteinander und die Nenner miteinander multipliziert.
Formel mit Platzhaltern
\( \frac{ \vartriangle }{ \square }\cdot \frac{\Diamond}{\bigcirc } = \frac{\vartriangle \cdot \Diamond}{\square \cdot \bigcirc } \)
Formel mit Variablen
\( \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Applet Erweitern und Kürzen von Brüchen Beispiel Bruchrechnung Addieren von Brüchen
Prozentrechnung, Proportionalität und Dreisatz
Prozentrechnung
Proportionalität
Dreisatz
Ein Auto verbrauche auf 100 km genau 7,8 Liter Benzin. Wie viel Liter werden für 480 km benötigt?
Offensichtlich sind beide Größen proportional zueinander, d.h. eine Verdopplung der Strecke hat eine Verdopplung des benötigten Benzins zu Folge.
Wir wollen die Frage mit Hilfe des Dreisatzes berechnen. Zunächst rechnen wir den Verbrauch für eine kleinere Einheit wie 1 km aus:
\( 100 \, km \, \hat{=} \, 7,8 \, Liter \) \( 1 \, km \, \hat{=} \, \frac{7,8}{100} \, Liter = 0,078 \, Liter \)
Damit können wir nun auf den Wert für eine Strecke von 480 km schließen:
\( 480 \, km \, \hat{=} \, 480 \cdot 0,078 \, Liter = 37,44 \, Liter \)
Wir hätten unsere "kleinere Einheit" aber auch größer wählen können, solange wir wieder so multiplizieren, dass wir auf 480 km kommen:
\( 10 \, km \, \hat{=} \, 0,78 \, Liter \) \( 480 \, km \, \hat{=} \, 48\cdot 0,78 \, Liter = 37,44 \, Liter \)
Nach einem sehr ähnlichen Prinzip geht man vor, wenn indirekte Proportionalität vorliegt. Angenommen zwei Baustellenarbeiter benötigen für die Pflasterung des Platzes 6h, wie lange benötigen dann drei Bauarbeiter?
Wir gehen wieder schrittweise vor:
\( 2 \, Bauarbeiter\, \hat{=} \, 6 \, h \)
\( 1 \, Bauarbeiter\, \, \, \hat{=} \, 2 \cdot 6 \, h = 12 \, h \)
\( 3 \, Bauarbeiter\, \hat{=} \, \frac{12}{3} \, h = 4 \, h \)
Also benötigen drei Bauarbeiter 4 Stunden.

1.4. Terme und Gleichungen

Terme und erste Gleichungen

Was ist ein Term?
Eine Gleichung besagt, dass zwei mathematische Ausdrücke gleich sind. Gleichheit wird durch das Gleichheits-Symbol „=“ ausgedrückt. Normalerweise enthält eine Gleichung eine oder mehrere Variablen oder Unbekannte. Lösungen der Gleichung sind Werte für die Variablen, so dass die Gleichung erfüllt ist.
Beispiel 1.
\( T(n)=2n \) mit \( n\in \mathbb{N} \)
Der Termausdruck beschreibt alle Vielfachen von zwei.
Grundmenge G. Wird in einen Term für die Variable eine Zahl aus der Grundmenge
G eingesetzt, so lässt sich der zugehörige Termwert berechnen.

- Eine dreistellige natürliche Zahl hat (von links nach rechts) die Ziffern x, y bzw. z. Gib den Term für diese Zahl sowie den Term' für ihre Quersumme an .
- Die Quersumme einer zweistelligen natürlichen Zahl hat den Wert 11 . Gib die Menge aller derartigen Zahlen an und finde einen passenden Term, der alle diese Zahlen beschreibt.
Ähnlich wie bei Brüchen können auch Terme äquivalent sein. Zwei Terme mit Variablen heißen äquivalent, wenn bei jeder möglichen Einsetzung für die Variablen der eine Term stets den gleichen Wert annimmt wie der andere.

- \( 4 + (a + 2) = a + 6\)
- \( 10y-y = 9y\)
- \( 2 \cdot x^2 + x = 5x\)
- \( 8x - 8 = x \)
- \( 14 \cdot 0 \cdot 5 = 70\)
- \( a + 2a + 2 = 3a + 2\)

Was ist eine Gleichung?
Eine Gleichung besagt, dass zwei mathematische Ausdrücke gleich sind. Gleichheit wird durch das Gleichheits-Symbol „=“ ausgedrückt. Normalerweise enthält eine Gleichung eine oder mehrere Variablen oder Unbekannte. Lösungen der Gleichung sind Werte für die Variablen, so dass die Gleichung erfüllt ist.
Beispiel 2.
a) \(5=5\) und \( 4x+2=2(2x+1) \) sind identische wahre Gleichungen: Sie sind wahr für alle Werte für Variablen.
b) \( 1=5 \) und \( x+3 = x+2 \) sind identisch falsche Gleichungen.
c) Die Gleichung \( 3x+1=7 \) ist genau dann wahr, wenn \( x=2 \). Für alle anderen Werte für \( x \) ist sie falsch.
d) Die Lösung der Gleichung \( 2x=ax+5 \) für variables \( x \) und festes \( a \) ist \( x=\frac{5}{2-a} \) unter der Annahme, dass \( a\ne 2 \). Wenn die elbe Gleichung in Bezug zu \( a \) gelöst wird, dann ist \( a=2-\frac{5}{x} \), wobei

Symbolisches Lösen
In diesem Teil werden fundamentale Methoden zur Lösungsfindung von Gleichungen mit einer Variablen behandelt mit dem symbolischen Lösen behandelt. Weitere Methoden werden im Kapitel Funktionen betrachtet, da für diese Lösungsmethoden weiteres Wissen vorausgesetzt wird.
Symbolisches oder algebraisches Lösen einer Gleichung beruht auf der Anwendung mathematischer Operationen auf beiden Seiten der Gleichung, um die Gleichung zu \( x=A \) zu verändern, wobei \( A \) ein Ausdruck ist, der \( x \) nicht enthält. Die häufigsten Operationen sind:
- Eine Zahl oder einen Term auf beiden Seiten der Gleichung addieren oder subtrahieren.
- Eine Zahl oder einen Term, die stets ungleich 0 sind, mit beiden Seiten der Gleichung multiplizieren. Diese Operation deckt auch die Division ab, da dividieren mit \( c \) äquivalent zur Multiplikation mit \( \frac{1}{c} \) ist
- Weiterhin gibt es Operationen wie das Ziehen einer Wurzel, quadrieren bzw. allgemein hoch n nehmen, den Logarithmus anwenden etc., welche auf beiden Seiten der Gleichung angewendet werden können.
Es ist wichtig zu erwähnen, dass nicht alle Operationen die Äquivalenz beibehalten. Bei den beiden ersten Punkten ist dies der Fall, man spricht von sogenannten Äquivalenzumformungen.
Zum Beispiel sind die beiden Gleichungen
\[x+1 = -3x+9 \]
und
\[ 4x=8 \]
äquivalent (in Zeichen \( x+1 = -3x+9 \quad \Leftrightarrow \quad 4x=8 \) ) , da beide die exakt gleichen Lösungen besitzen. Diese können durch die Äquivalenzumformung \( "+ 3x , \, - 1" \) ineinander überführt werden.
Wir wollen zwei Beispiele betrachten, wo Vorsicht geboten ist:
- \( \sqrt{x}=6-x \) kann mit der Umformung "Quadrieren" in die Gleichung \( x=(6-x)^2 \) überführt werden. Beide Gleichungen sind aber nicht äquivalent, da die erste nur für \( x=4 \) wahr ist, die zweite Gleichung aber für \( x=4 \) und \( x = 9 \). Wir haben also eine Lösung "dazugewonnen", die keine ist.
- \( x^2 = 25 \) kann mit der Umformung "Quadratwurzel ziehen" in die Gleichung \( x = 5 \) überführt werden, da die Wurzel stets positives Vorzeichen besitzt. Offensichtlich haben wir aber die Lösung \( x = -5 \) der ersten Gleichung "verloren".
Bei beiden Operationen handelt es sich nicht um Äquivalenzumformungen, es sind aber dennoch essentielle Operationen zum Lösen von Gleichungen. Eine Methode dieses Problem zu Umgehen ist die Verwendung des Zeichens \( \Rightarrow \), z.B in der Form
\[ x^2 = 25 \Rightarrow x = \pm 5 \]

1.5. lineare und quadratische Gleichungen

Lineare und Quadratische Gleichungen

Lineare Gleichungen
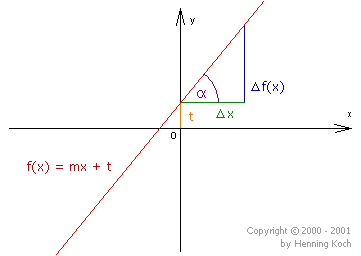
Eine lineare Gleichung oder eine Polynomgleichung ersten Grades, ist eine Gleichung der Form \[ ax = b, a \ne 0 \] und durch Division durch \( a \) erhält man ihre eindeutige Lösung \[ x=\frac{b}{a}. \] Geometrisch ist dies die Nullstelle der Geraden \( y=ax-b \).

Quadratische Gleichungen
Eine quadratische Gleichung oder auch eine Polynomgleichung zweiten Grades, sind Gleichungen der Form \[ ax^2+bx+c = 0, a \ne 0 \] und ihre Lösung ist durch die Lösungsformel für quadratische Gleichungen (Mitternachtsformel oder abc-Formel) \[ x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, \] gegeben, unter der Annahme, dass die Diskriminante \( b^2-4ac \) nicht negativ ist. Wahlweise kann auch die pq-Formel angwandt werden, hierfür muss aber der Koeffizient vor \( x^2 \) gleich 1 sein.
Wenn die Diskriminante (lat. discriminare = unterschieden) Null ist, gibt es nur exakt eine Lösung \( x=\frac{-b}{2a} \). Wenn die Diskriminante negativ ist, gibt es überhaupt keine reellen Nullstellen, aber stattdessen gibt es zwei komplexe Nullstellen. Diese werden im Kapitel Komplexe Zahlen besprochen. Ist die Diskriminante echt positiv, dann gibt es zwei echt-verschiedene reelle Lösungen.
Manchmal gibt es leichtere Wege als die Lösungsformel, um quadratische Gleichungen zu lösen:
- Wenn \( b=0 \), kann die Gleichung in der Form \( x^2 = d \) (mit \( d=\frac{-c}{a} \) ). geschrieben werden. Hier hat die Gleichung die Lösungen \( x=\pm \sqrt{d}, \) wenn \( d \geq 0 \).
- Wenn \( c=0 \), kann die Gleichung durch Ausklammern in der Form \( x \cdot (ax+b) = 0 \) geschrieben werden. Der Satz vom Nullprodukt ("Null-Produkt-Regel") für reelle Zahlen besagt, dass das Produkt \( AB \) genau dann null ist, wenn \( A=0 \) oder \( B=0. \) Somit hat die Gleichung \( x \cdot (ax+b) = 0 \) zwei Lösungen \( x=0 \) und \( x=-\frac{b}{a}\).
Beispiel 1.
Die Gleichung \[ 2x^2+3x=0 \] kann durch Anwenden des Satzes vom Nullprodukt gelöst werden: Ausklammern des gemeinsamen Faktors \( x \) liefert \[ x(2x+3)=0 \] und somit sind die Nullstellen \[ x=0 \textrm{ und } x=-\frac{3}{2}. \]
Beispiel 2.
Anwenden der Lösungsformel für quadratische Gleichungen auf die Gleichung \[ 2x^2-7x+6=0. \] liefert \[ x= \frac{7 \pm \sqrt{(-7)^2 - 4\cdot 2 \cdot 6}}{2\cdot 2} = \frac{7 \pm 1}{4}. \] Also sind die Nullstellen \[ x_1 = 2 \textrm{ und } x_2 = \frac{3}{2}. \]
Beispiel 3.
Wenn die quadratische Formel auf die Gleichung \[ x^2+2x+2=0, \] angewandt wird, ist die Diskriminante eine negative Zahl \( 2^2-4\cdot 1 \cdot 2 = -4\). Somit hat die Gleichung keine reellen Lösungen.

Gleichung ersten Grades im Komplexen Zahlenraum
Eine Gleichung der Form (oder abgeänderter Form) \[ az+b=0, \] mit \( a,b,z \in \mathbb{C}, \) kann ähnlich wie Gleichungen ersten Grades einer reellen Variablen gelöst werden. Typischerweise ist die Lösung ein Quotient/Bruch zweier komplexer Zahlen. Mithilfe der Identität \( z\overline{z} = |z|^2 \) kann man diesen in die bekannte Form überführen, indem man mit dem komplex kojugierten des Nenners erweitert.
Beispiel 2.
Lösen wir die Gleichung \[ 2z-3iz-2i=5. \] Die Gleichung kann geschrieben werden als \[ (2-3i)z = 5+2i \] und die Lösung ist \[ z=\frac{5+2i}{2-3i} = \frac{(5+2i)\cdot (2+3i)}{(2-3i)\cdot (2+3i)} = \frac{10+15i+4i+6i^2}{4+6i-6i-9i^2} \] und weiter \[ z = \frac{4+19i}{13} = \frac{4}{13}+\frac{19}{13}i. \]

Gleichung zweiten Grades im Komplexen Zahlenraum
Wie bereits bekannt ist, besitzt die quadratische Gleichung \[ ax^2+bx+c=0 \] keine reellen Lösungen, wenn die Diskriminante \( b^2-4ac \) negativ ist. Jedoch kann bewiesen werden, dass in diesem Fall die Gleichung die imaginären Lösungen \[ x=\frac{-b\pm i\sqrt{-(b^2-4ac)}}{2a} \] hat - die Mitternachtsformel also letztlich ihre Gültigkeit beibehält.
Dies kann durch direktes Rechnen gesehen werden: \[ a\Big(x-\frac{-b + i\sqrt{-(b^2-4ac)}}{2a}\Big)\Big(x-\frac{-b - i\sqrt{-(b^2-4ac)}}{2a}\Big) = ax^2+bx+c, \] somit zerfällt das Polynom \( ax^2+bx+c \) als Produkt in die Faktoren \( x-\frac{-b \pm i\sqrt{-(b^2-4ac)}}{2a} \) und hat somit die Nullstellen \( \frac{-b \pm i\sqrt{-(b^2-4ac)}}{2a}. \)
Beispiel 3.
Anwenden der Mitternachtsformel auf die Gleichung \[ z^2-8z+20 = 0 \] liefert \[ z=\frac{8 \pm \sqrt{(-8)^2-4\cdot 1 \cdot 20}}{2\cdot 1} = \frac{8 \pm \sqrt{-16}}{2}. \] Da die Diskriminante negativ ist, gibt es keine reellen Lösungen, aber zwei imaginäre Lösungen \[ z= \frac{8 \pm i\sqrt{16}}{2} = \frac{8 \pm 4i}{2} = 4 \pm 2i. \]

Vergleich von Real- und Imaginärteil
Per Definition sind zwei komplexen Zahlen gleich, wenn sowohl der Realteil als auch der Imaginärteil übereinstimmen. Mit diesem Prinzip können viele komplexe Gleichungen mit einem Paar an Gleichungen, bei denen Real- und Imaginärteil der linken und rechten Seite der Gleichung gleich gesetzt werden, gelöst werden.
Beispiel 4.
Die Gleichung \[ 2\overline{z}+|z|^2=13-6i \] kann gelöst werden, indem wir \( z \) als \( z=x+iy \) schreiben, also \( \overline{z}=x-iy \) und \( |z|^2=x^2+y^2 \). Dies führt zu zwei simultanen Gleichungen \[ \begin{cases} 2x+x^2 + y^2= 13 \\ -2y=-6. \end{cases}\] Die zweite Gleichung liefert \( y=3 \) . Durch Einsetzen in die erste Gleichung und Anwenden der Mitternachtsformel liefert \( x=-1\pm \sqrt{5}\) . Somit ist die Lösung \[ z = -1 \pm \sqrt{5}+3i.\]

Binomische Gleichungen im Komplexen Zahlenraum
\[ z^n = a \] kann gelöst werden, indem die Variable \( z \) und die Konstante \( a \) in exponentieller Form dargestellt werden und durch Verwendung des Prinzips, dass zwei komplexe Zahlen gleich sind, wenn ihre Beträge und ihre Argumente gleich sind bzw. die Differenz der Argumente ein ganzzahliges Vielfaches von \( 2\pi \) ist.
Beispiel 5.
Die Gleichung \[ z^3=-2+i2\sqrt{3} \] kann geschrieben werden als (siehe den Abschnitt Konjugation, Betrag und Argument und Beispiel 1) \[ |z|^3e^{i3\phi} = 4e^{i\frac{2\pi}{3}}. \] Die komplexen Zahlen auf beiden Seiten der Gleichung sind gleich, wenn
- Die Beträge gleich sind: \[ |z|^3 =4 \Leftrightarrow |z|=4^{\frac{1}{3}} \]
- Und wenn die Argumente gleich sind oder sich durch ein ganzzahliges Vielfaches von \( 2\pi \) unterscheiden: \[ 3\phi = \frac{2\pi}{3} + n2\pi \Leftrightarrow \phi = \frac{2\pi}{9} + n\frac{2\pi}{3}. \]
Nun erhalten wir die Antworten mit unterschiedlichen Werten von \( n \) als \[ z_0 = 4^{\frac{1}{3}}e^{i \frac{2\pi}{9}} = 4^{\frac{1}{3}}(\cos(\frac{2\pi}{9})+i\sin(\frac{2\pi}{9})) \approx 1.21 + 1.02i. \] Auf ähnliche Art und Weise kann man sehen, dass \[ z_1 \approx -1.49+0.54i \] und \[ z_2 \approx 0.28-1.56i.\] Es gibt keine weiteren Lösungen, da \( z_3=z_0, z_4=z_1 \) etc. und für eine Gleichung von Grad \( n \) ist die maximale Anzahl an verschiedenen Nullstellen gleich \( n \).

1.6. Exponentielle und logarithmische Gleichungen

Nichtlineare Gleichungen
In diesem und dem folgenden Kapitel werden wir weitere Gleichungen betrachten, die sich nicht in lineare oder quadratische Gleichungen einordnen lassen.
In diesem Kapitel werden wir dafür die Folgenden Gleichungsklassen betrachten:
- Exponentielle Gleichungen
- Logarithmische Gleichungen

Exponentielle und Logarithmische Gleichungen
Lösen einer exponentiellen Gleichung
Aufgrund der Definition des Logarithmus, hat die Exponentialfunktion (angenommen \( a, k > 0 \) ) \[ k^x = a \] eine eindeutige Lösung \[ x=\log_k a. \] Die Lösung wird durch den Logarithmus zur Basis \( k \). ausgedrückt. Ein alternativer Weg die Gleichung zu lösen ist den natürlichen Logarithmus (Logarithmus zur Basis \( e \), bezeichnet als \( \ln \)) auf beiden Seiten anzuwenden: \[ \ln k^x = \ln a. \] Nun kann die Regel \( \log_k a^r = r\log_k a\) auf die Gleichung angewendet werden \[ x \ln k = \ln a \] welche die Lösung \[ x = \frac{\ln a}{\ln k} \] hat. Welche Variante verwendet wird, ist letztlich Geschmackssache, da beide Terme durch einen "Basiswechsel" ineinander überführt werden können.
In der Anwendung müssen exponentielle Gleichungen oft verändert werden bevor der Logarithmus auf beiden Seiten angewendet werden kann, wie folgendes Beispiel zeigt.
Beispiel 1.
Lösen wir die Gleichung \[ 2{,}5\cdot 1{,}2^x = 23. \] dividieren beider Seiten mit \( 2{,}5 \) und Anwenden des Logarithmus liefert: \[ \ln 1{,}2^x = \ln \frac{23}{2{,}5} \] oder \[ x \ln 1{,}2 = \ln 9{,}2. \] Somit ist die Lösung \[ x = \frac{\ln 9{,}2}{\ln 1{,}2} (=log_{1,2} {9,2}) \approx 12{,}2. \]
Beispiel 2.
Das Vermögen \( A \) ist mit einem jährlichen Zinsbetrag von 4 % verzeichnet. Wenn es keine weiteren Transaktionen gibt, ist die Menge an Geld auf dem Sparkonto eine Funktion abhängig von der Zeit \[ f(t)=A\cdot 1{,}04^t , \] wobei \( t \) die Zeit in Jahren ist (um genau zu sein, ist das Modell für ein ganzzahliges t exakt und kann leicht inakkurat für nicht-ganzzahlige Werte sein, je nach Richtlinie der Bank). Wie viele Jahre dauert es bis sich das Kapital verdoppelt? Das Problem ist äquivalent zum Lösen der Gleichung \[ A\cdot 1{,}04^t = 2A \] oder \[ 1{,}04^t = 2, \] mit der Lösung \[ t = \frac{\ln(2)}{\ln(1{,}04)} \approx 17{,}7. \] Also dauert es ungefähr 18 Jahre bis sich das Kapital verdoppelt.
Beispiel 3.
Nach dem Newtonschen Abkühlungsgesetz ist die Temperatur \( T \) eines abkühlenden Objektes als Funktion abhängig von der Zeit \[ T(t)=T_a+(T_0-T_a ) e^{-kt}, \] wobei \( T_0 \) die Anfangstemperatur, \( T_a \) die Umgebungstemperatur und \( k \)eine Konstante abhängig von Material und Geometrie des Objektes ist.
Betrachten wir ein Szenario, bei dem die Innentemperatur eines Hauses \( 24.0^\circ \textrm{C} \) und die Außentemperatur \( -21^\circ \textrm{C} \) beträgt. Dann wird der Strom abgeschnitten und die Heizung funktioniert nicht mehr. Innerhalb von 120 Minuten sinkt die Temperatur auf \( 19.0^\circ \textrm{C} \). Unter der Annahme, dass Newtons Abkühlungsgesetz in diesem Fall anwendbar ist, suchen wir einen passenden Wert für den Parameter \( k \).
Nehmen wir Stunden als Einheit. Es gilt \[ T(2 \, \textrm{h}) = (-21+45e^{-k\cdot 2 \textrm{h}})^\circ \textrm{C} = 19^\circ \textrm{C}. \] Also ist \[ e^{-k\cdot 2 \, \textrm{h}} = \frac{19 + 21}{45} = \frac{8}{9}. \] Nun kann der natürliche Logarithmus angewendet werden, um die Lösung zu erhalten: \[ -k \cdot 2 \, \textrm{h} = \ln (\frac{8}{9}). \] Dividieren beider Seiten mit \( 2 \, \textrm{h} \) liefert \[ k = \frac{\ln (\frac{8}{9})}{-2 \, \textrm{h} } \approx 0{,}05889 \, \frac{1}{\textrm{h}}. \]

Übung
- Löse die Gleichung \[3^{x}+3^{x+2}=30.\]
- Löse die Gleichung \[2^{x^2-1}-3^{x^2-1}=3^{x^2}-2^{x^2+2}.\]
- Löse die Gleichung \[\left(\frac{5}{11}\right)^x+4\left(\frac{11}{5}\right)^x=5.\]
- Löse die Gleichung \[3^x+4^x=7.\]

Lösen einer logarithmischen Gleichung
Beispiel 5.
Die Dezibel-Skala wird genutzt, um bspw. den Lautstärkepegel zu messen (aber dies ist nicht die einzige Anwendung). Der Lautstärkepegel in Dezibel wird definiert als \[ L=10 \lg \frac{I}{I_0} \textrm{ dB} \] wobei \( I \) die Intensität der Lautstärke ist (als Watt pro Quadratmeter), \( I_0\approx 10^{-12} \frac{\textrm{W}}{\textrm{m}^2} \) ist die Schwelle menschliche Hörens in der Luft und \( \lg \) ist der Logarithmus zur Basis 10.
Nehmen wir an, dass Musik mit einer Lautstärke von 60 Dezibel gespielt wird und dann auf 82 Dezibel aufgedreht wird. Wie groß ist die Zunahme der Intensität der Lautstärke? Bestimme das Verhältnis der Intensitäten.
Zuerst lösen wir die logarithmische Gleichung \[ L=10 \lg \frac{I}{I_0} \textrm{ dB} \] für die Intensität \( I \). Dividieren beider Seiten mit \( 10 \textrm{ dB} \) liefert \[ \lg \frac{I}{I_0} = \frac{L}{10 \textrm{ dB}} \] oder \[ I = I_0 \cdot 10^{\frac{L}{10 \textrm{ dB}} } . \] Somit ist die Intensität der Lautstärke von 60 dB \( I_1 = I_0 \cdot 10^6 \) und die Intensität der Lautstärke von 82 dB \( I_2 = I_0 \cdot 10^{8{,}2} \), das Verhältnis zwischen den beiden ist \[ \frac{I_2}{I_1} = \frac{ I_0 \cdot 10^{8{,}2} }{I_0 \cdot 10^6} = 10^{2{,}2} \approx 158. \]
1.7. Trigonometrische Gleichungen

Trigonometrische Gleichungen
Allgemeine Grundlagen zum Lösen trigonometrischer Gleichungen
Dieses Kapitel führt kurz grundlegende Verfahren zum Lösen trigonometrischer Gleichungen ein und veranschaulicht diese durch ein paar Beispiele. Folgende Verfahren zum Lösen von Sinus, Cosinus und Tangens-Gleichungen sind Folgerungen aus elementaren Eigenschaften von Sinus, Cosinus und Tangens, wie der Periodizität und der Definition der inversen trigonometrischen Funktionen. Unten nimmt \( n \) alle ganzzahligen Werte an. Für Eigenschaften der trigonometrischen Funktionen und graphische Darstellungen, siehe auch das Kapitel Trigonometrische Funktionen.

Sinus-Gleichung
Angenommen \( a \in [-1,1] \), so hat die Gleichung \[ \sin(x)=a \] unendlich viele Lösungen \[ x = \arcsin(a)+n \cdot 2\pi \hspace{0.3cm} \textrm { , } \hspace{0.3cm} x = \pi - \arcsin(a)+n \cdot 2\pi. \] Warum hat die Gleichung diese Lösungen? Zuerst ist der \( \arcsin(a) \) definiert als ein Wert \( x \) auf dem Intervall \( [-\frac{\pi}{2}, \frac{\pi}{2}] \), so dass \( \sin(x) = a \). Also ist offensichtlich zumindest der \( \arcsin(a) \) eine Lösung. Zweitens gibt es die anderen Lösungen wegen der Periodizitäts-Eigenschaft \( \sin(x)=\sin(x+n\cdot 2 \pi) \). Zuletzt ist \( \sin(x) = \sin(\pi - x) \) mit allen Werten von \( x \), weshalb auch \( x = \pi - \arcsin(a)+n \cdot 2\pi\) Lösungen sind.

Cosinus-Gleichung
Ist wiederum angenommen \( a \in [-1,1] \), so hat die Gleichung
\[ \cos(x)=a \]
die Lösungen
\[ x = \pm \arccos(a)+n \cdot 2\pi. \]
Die Situation ist sehr ähnlich zu der Sinus-Gleichung. Während die Sinus-Funktion gleiche Werte in den Punkten \( x \) und \( \pi - x \) hat, gilt für Cosinus die Identität \( \cos(x) = \cos(-x) \) erfüllt, woraus die obigen Lösungen folgen. Beachte, dass \( \arccos(a) \) immer per Definition im Intervall \( [0, \pi ] \) liegt.

Tangens-Gleichung
Lösungen der Tangens-Gleichung \[ \tan(x)=a \] sind \[ x = \arctan(a)+n \cdot \pi. \] Dies liegt an der Definition des \( \arctan(a) \) (welcher immer im offenen Intervall \( ]-\frac{\pi}{2}, \frac{\pi}{2}[ \) liegt) und der Tatsache, dass \( \tan(x) = \tan(x+n\cdot \pi) \) für alle ganzzahligen Werte von \( n \) gilt.
Beachte, dass die Tangens-Gleichung \( \tan(x)=a \) Lösungen für alle reellen Werte von \( a \) besitzt, wohingegen die Gleichungen \( \sin(x)=a \) und \( \cos(x)=a \) keine Lösungen besitzen, wenn \( a \) nicht im Intervall \( [-1,1] \) liegt.
Beispiel 6.
Löse die Gleichung \[ \cos\left(3x+\frac{\pi}{6}\right) = \frac{1}{2}. \] Da \( \arccos(\frac{1}{2}) = \frac{\pi}{3} \), kann die Gleichung folgendermaßen gefunden werden: \[ \cos\left(3x+\frac{\pi}{6}\right) = \frac{1}{2} \] \[3x+\frac{\pi}{6} = \pm \frac{\pi}{3} + 2\pi n \] \[ 3x = \frac{\pi}{6} +2\pi n \hspace{0.3cm} \textrm{ oder } \hspace{0.3cm} 3x = -\frac{3\pi}{6} + 2\pi n \] \[x = \frac{\pi}{18} + \frac{2\pi}{3}n \hspace{0.3cm} \textrm{ oder } \hspace{0.3cm} x = -\frac{\pi}{6} +\frac{2\pi}{3}n. \]
Beispiel 7.
Nehmen wir an, dass eine alternierende elektrische Spannung als Funktion abhängig von der Zeit ist \[ I(t) = 350 \textrm{V} \sin(294 \frac{1}{\textrm{s}} t + 0{,}02 \textrm{s}). \] Bestimme alle (Zeit-)Punkte auf dem Intervall \( t\in [0 ; 0{,}05 \textrm{s} ] \), so dass \( I(t) = 210 \textrm{V} \). Gib die Antwort in Sekunden mit einer Genauigkeit von vier Nachkommastellen an.
Lösung: Nun ist die Aufgabe die Gleichung \[ 350 \textrm{V} \sin(294 \frac{1}{\textrm{s}} t + 0{,}02 \textrm{s}) = 210 \textrm{V} \] zu lösen, unter der Annahme, dass \( t\in [0 ; 0{,}05 \textrm{s} ] \). Dividieren beider Seiten mit \( 350 \textrm{V} \) liefert \[ \sin(294 \frac{1}{\textrm{s}} t + 0{,}02 ) = 0{,}6. \] Somit sind alle Lösungen durch die Gleichungen \[ 294 \frac{1}{\textrm{s}} t + 0{,}02 = \arcsin(0{,}6) + n\cdot 2\pi \] und \[ 294 \frac{1}{\textrm{s}} t + 0{,}02 = \pi - \arcsin(0{,}6) + n\cdot 2\pi \] gegeben. Ab diesem Schritt werden angenäherte Werte verwendet. Man kann es als den eleganteren Weg sehen, den Lösungsprozess mit genauen Werten zu vervollständigen aber in diesem Fall kann es leichter sein die Ausdrücke zu lesen und zu verstehen, wenn gerundete Werte verwendet werden Da \( \arcsin(0{,}6) \approx 0{,}64350 \), kann die erste Gleichung als \[ t \approx \frac{1}{294}(0{,}6435-0{,}02+n\cdot 2\pi) \textrm{ s} \] \[ \approx (0{,}002121 + n\cdot 0{,}02137)\textrm{ s} \] geschrieben werden und die zweite als \[ t \approx (0{,}008429 + n\cdot 0{,}02137)\textrm{ s}. \] Nun werden nur Lösungen im Intervall \( [0 ; 0{,}05 \textrm{ s} ] \) akzeptiert. Negative Werte von \( n \) liefern eine negative Zeit, also stehen sie nicht zur Debatte. In der ersten Gleichung ist \( t\leq 0{,}05 \textrm{s} \), wenn \( n \) die Werte 0, 1 oder 2 annimmt. In der zweiten Gleichung sind akzeptable Werte für \(n \) nur 0 und 1. Somit gibt es fünf verschiedene Lösungen und mit einer Genauigkeit von drei Nachkommastellen sind dies \[ 0{,}002 \textrm{ s} \textrm{ , } 0{,}008 \textrm{ s} \textrm{ , } 0{,}023 \textrm{ s} \textrm{ , } 0{,}030 \textrm{ s} \textrm{ und } 0{,}045 \textrm{ s}. \]
Beispiel 8.
Löse die Gleichung \[ \sin(4x+1) = \cos(4x+1). \] Dividieren beider Seiten mit \( \cos(4x+1) \) und wir erinnern uns, dass \( \tan(x)=\frac{\sin(x)}{\cos(x)} \), so erhalten wir \[ \frac{\sin(4x+1)}{\cos(4x+1)} = 1 \] \[tan(4x+1) = 1 \] \[4x+1 = \frac{\pi}{4}+\pi n \] \[x = \frac{\pi - 4}{16}+ \frac{\pi}{4}n. \]

1.8. Aufgaben


Aufgaben zum 1. Kapitel
Aufgabe 1.
Aufgabe 2.
Der Gesamt-Widerstand zweier Widerstände, die parallel geschaltet sind, ist durch die Formel \[ \frac{1}{R_{tot}} = \frac{1}{R_1}+\frac{1}{R_2} \] gegeben. Nehmen wir an, dass es notwendig ist, dass der Unterschied zwischen den Widerständen \( R_1 \) und \( R_2 \) gleich \( 1{,}5 \Omega\) beträgt und der Gesamt-Widerstand \( 4 \Omega \) ist. Bestimme die Widerstände \( R_1 \) und \( R_2 \). (Tipp: Bezeichne \( R_1 = x \), drücke \( R_2 \) mithilfe von \( x \) aus und du erhältst eine Gleichung mit einer Variablen.)
Aufgabe 3.
Löse die Gleichung \[ (\tan(x))^2+(1-\sqrt{3})\cdot \tan(x)-\sqrt{3}=0 \] unter der Annahme, dass \( x \in [-\frac{\pi}{2},\frac{\pi}{2}] \). (Tipp: Bezeichne zuerst \( \tan(x)=t \) und löse die quadratische Gleichung für \( t \). Löse dann die Gleichung \( \tan(x)=t \) für \(x\).)
Aufgabe 4.
Die Schallleistung eines Lautsprechers ist \( 0{,}2\) Watt. Nehmen wir an, das sich der Ton kugelförmig ausbreitet: im Abstand \( r \) breitet sich der Schall auf einer Fläche von \( 4 \pi r^2 \). aus. Wie ist der Lautstärkepegel, wenn der Abstand vom Lautstärker
- 1 m
- 5 m
beträgt?
Aufgabe 5.
Vereinfache den Ausdruck \[ \frac{zu}{z+u} \] wobei \( z=2+3i \) und \( u=-1+2i \). Drücke die Antwort in Form von \( a+bi \) aus.
Aufgabe 6.
Löse die Gleichungen (\(z\in \mathbb{C})\).
- \( z(3-4i)=5z+i \)
- \( \frac{i}{z}=\frac{1+2i}{z+1} \)
- \( z^2-6z+58=0 \)
- \( z^3=-4+4i \)
Hinweis für d): Siehe Beispiel 5.
Aufgabe 7.
Löse die Gleichungen ( \( z\in \mathbb{C} ) \).
- \( |z|+\overline{z}=2-3i \)
- \( z-\overline{z}=|z|^2+2 \)
Hinweis: Bezeichne \( z=x+yi \).

2. Folgen und Grenzwerte


Das Kapitel Folgen und Grenzwerte umfasst:

- Definitionen und Darstellung einer Folge
- Wichtige Beispiele für Folgen
- Elementare Eigenschaften von Folgen
- Grenzwerte
- Aufgaben

2.1. Definitionen und Darstellung einer Folge

Dieser Abschnitt stellt die wichtigsten Definitionen über Folgen vor. Diese Definitionen erklären die allgemeine Schreibweise von Folgen, aber wir schränken uns danach auf reelle Folgen ein.
Würde man \[\left( 3, ~1, ~4, ~1, ~5, ~9, ~2, ~6 \right) \] und \[ \left( 1, 1, ~2, ~3, ~4, ~5, ~6, ~9 \right) \]
als verschiedene Objekte bezeichnen? Oder würde man sagen, dass sie in einer gewissen Weise gleich sind? Wann würde man sie als gleich und wann würde man sie als verschieden bezeichnen?
Der Schlüssel zum Vergleich ist die Reihenfolge. Sobald die Reihenfolge der Zahlen als Kriterium herangezogen wird, sind die beiden Objekte verschieden. Wird die Reihenfolge der Zahlen nicht als Kriterium herangezogen, können die Objekte als Mengen mit jeweils 8 Elementen betrachtet und als gleich bezeichnet werden.
Aber wie legt man eine Reihenfolge fest? Am einfachsten wäre eine Aufzählung:
-
das erste Element ist 3;
-
das zweite Element ist 1;
-
das dritte Element ist 4;
-
das vierte Element ist 1;
-
das fünfte Element ist 5;
-
usw....
Wir haben eben eine natürliche Zahl (genauer genommen eine Ordinalzahl) jedem Ausdruck zugewiesen. Die Reihenfolge ist nun fixiert. Wie in diesem Kurs noch erklärt wird, wird durch Zuweisung eine Funktion beschrieben. Aber in diesem Fall hat die Funktion einen speziellen Definitionsbereich, nämlich die Menge der natürlichen Zahlen \( \mathbb{N} \). Allgemeiner würde sich auch jede Menge mit zu den natürlichen Zahlen \( \mathbb{N} \) äquivalenten Eigenschaften zur Nummerierung eignen. Ein Beispiel hierfür ist die Menge der ganzen Zahlen \( \mathbb{Z} \). Auch bestünde die Möglichkeit nur eine (endliche) Teilmenge der natürlichen Zahlen als Definitionsmenge zu benutzen.
Wir werden im Folgenden aber immer die natürlichen Zahlen als Definitionsbereich verwenden. Außerdem möchten wir das bisherige in einer mathematischen Definition festhalten.
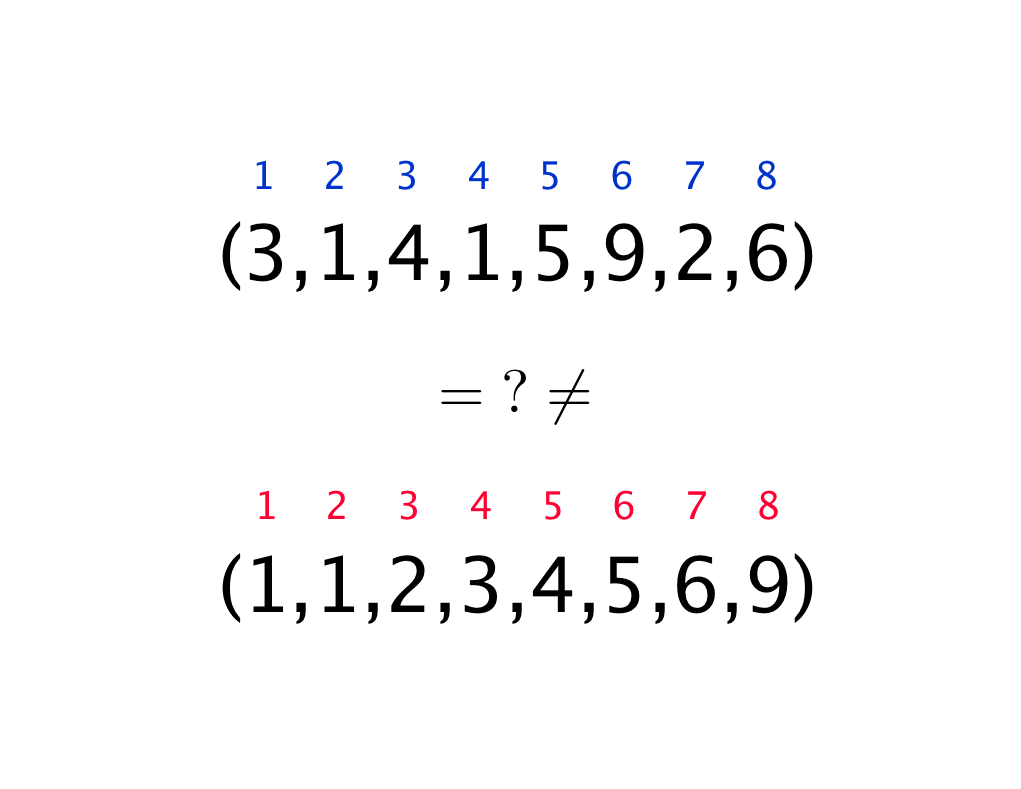

Definition 1 (Folge)
Eine Abbildung \[ a:\mathbb{N} \to \mathbb{M},\] die jeder natürlichen Zahl eine Zahl zuordnet, heißt eine (unendliche) Folge. Anstelle von \( \mathbb{N} \) kann auch \( \mathbb{N_0} \) als Definitionsbereich gewählt werden. Die Funktionswerte einer Folge werden im Unterschied zur klassischen Notation bei Funktionen mit \( a_n \) statt \( a(n) \) bezeichnet und die Glieder der Folge genannt. \( n \) wird Index der Folge genannt.
Spezialfall:
Eine Abbildung \[ a:\mathbb{N} \to \mathbb{R},\] die jeder natürlichen Zahl eine reelle Zahl zuordnet, heißt eine (unendliche) Folge reeller Zahlen, eine reelle Zahlenfolge, eine Folge in \( \mathbb{R} \) oder auch kurz eine Folge.
Kurz gesagt: Eine Folge ist eine unendliche Aufzählung von Elementen.
Um eine Folge von der Menge ihrer Glieder zu unterscheiden, werden oft die Symbole
\[ (a_n)_n \text{ oder } (a_n) \]
verwendet. Ist durch Angabe der ersten Folgenglieder offensichtlich, welchem Bildungsgesetz die Folge genügt, so kann sie auch in der Form
\[ (a_1, a_2, a_3, a_4, ...) \]
angegeben werden. Folgen werden in der Regel mit den Anfangsbuchstaben des Alphabets bezeichnet.
Folgen sind besondere Funktionen. Daher werden sie durch eine besondere Notation von der üblichen Bezeichnung für Funktionen (nämlich \( f \)) unterschieden. Man schreibt \( (a_n) \) anstatt \( a \) :
\( a: \mathbb{N} \longmapsto \mathbb{M} \)
\( n \mapsto a_n \)
\( a_n \) wird als \( n-tes \) Folgenglied der Folge \( a \) gelesen, wobei die gesamte Folge mit \( \left( a_n \right)_{n \in \mathbb{N}} \) oder \( \left( a_n \right) \) bezeichnet wird. Die Zahl n wird als Index des Folgenglieds \( a_n \) bezeichnet.
Beispiel 1.
Manchmal müssen einige Ideen kombiniert werden. So wird die Folge
\( 2,~~0,~-8,~~0,~~32,~~0,~-128,~... \) definiert durch
\( a_n=\cos(\frac{\pi}{2}(n-1)) \cdot 2^n \) für \( n\in\mathbb{N} \) .


Übung 2.
Finde eine Formel, welche die Folge \( 0, ~\frac{1}{2}, ~\frac{2}{3}, ~\frac{3}{4}, ~\frac{4}{5}, \dots \) beschreibt.
Darstellung von Folgen
Es gibt verschiedene Methoden um Folgen zu definieren. In diesem Abschnitt stellen wir die gebräuchlichsten Methoden vor. Dazu gehören:
- Explizite Forme
- Rekursion
- Beschreibende Definition

Explizite Formel
Eine Folge kann durch eine explizite Formel für das \( n\)-te Element dargestellt werden. Jedoch kann nicht jede Folge durch eine Formel definiert werden.
Beispiel 2:
Die Formel \( a_n = \frac{n^2+n}{2}\) erzeugt die Folge:
| \(a_{n}\) | \(a_{1}\) | \(a_{2}\) | \(a_{3}\) | \(a_{4}\) | \(a_{5}\) | \(\ldots\) | \(a_{10}\) | \(\ldots\) | \(a_{42}\) | \(\ldots\) |
| 1 | 3 | 6 | 10 | 15 | \(\ldots\) | 55 | \(\ldots\) | 903 | \(\ldots\) |
Als Resultat liefert die Formel wegen der Gaußschen Summationsformel (mehr dazu) die Summe aller natürlichen Zahlen zwischen 1 und n :
\[ \frac{n^2+n}{2} = \frac{n\cdot (n+1)}{2} = \sum\limits_{k=1}^n k \]
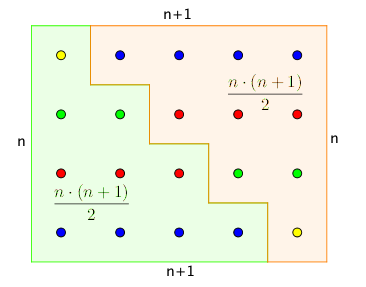
Eine explizite Formel erlaubt es, ohne eine Vielzahl an Berechnungen einerseits direkt jedes beliebige Element einer Folge zu berechnen und andererseits zu prüfen, ob eine gegebene Zahl in der Folge auftritt.

Übung 3.
Gegeben sei die Folge von Beispiel 2. Gehören die Zahlen \( 78 \) und \( 100 \) zu dieser Folge?

Rekursion
Im Gegensatz zur expliziten Formel können die Elemente einer Folge auch durch ihre Beziehungen untereinander spezifiziert werden. Betrachten wir das folgende Beispiel:
-
das erste Element der Folge \(\left( b_n \right)\) ist \( b_0=12\);
-
jedes weitere Element der Folge ist das doppelte des vorhergehenden Elements.
Diese Bedingungen genügen, um alle alle Elemente der Folge zu definieren:
| \(b_{n}\) | \(b_{1}\) | \(b_{2}\) | \(b_{3}\) | \(b_{4}\) | \(b_{5}\) | \(\ldots\) | \(b_{n-1}\) | \(b_n\) | \(\ldots\) |
| 12 | 24 | 48 | 96 | 192 | \(\ldots\) | \(2b_{n-2}\) | \(2b_{n-1}\) | \(\ldots\) |
Dies kann kurz wie folgt geschrieben werden:
-
\(b_1 = 12\);
-
\(b_n = 2b_{n-1}\).
Diese Methode der Definition einer Folge heißt rekursiv und basiert auf dem Prinzip der Rekursion. Im Allgemeinen können zur rekursiven Berechnung von Folgengliedern alle bisher berechneten Folgenglieder herangezogen werden:
\[a_n = F(a_{n-1}, a_{n-2}, ... , a_{n-k}), \text{ wobei }k \geq 1\]
Eine sehr populäre rekursiv definierte Folge ist die Fibonacci Folge, die im nächsten Kapitel behandelt wird.
Natürlich ist es meist einfacher, mit einer expliziten Formel zu arbeiten. Allerdings ist diese nicht immer zu Beginn bekannt. Wir werden im nächsten Abschnitt Beispiele von Folgen besprechen, die sowohl explizit als auch rekursiv definiert werden können.

Beschreibende Definition
Nicht immer kann eine Folge durch eine explizite oder rekursive Formel definiert werden. Einige Folgen können überhaupt nicht oder nur schlecht durch eine Formel definiert werden, obwohl ihre Struktur einfach und klar ist. Betrachte als Beispiel die folgende Folge:
| \(a_{n}\) | \(a_{1}\) | \(a_{2}\) | \(a_{3}\) | \(a_{4}\) | \(a_{5}\) |
| 3.1 | 3.14 | 3.141 | 3.1415 | 3.14159 |
Offensichtlich stellen die Folgenglieder eine Näherung der Zahl \(\pi\) mit zunehmender Genauigkeit dar. Die Folge kann durch "Das \(n-te\) Element der Folge entsteht durch Abschneiden der Dezimaldarstellung von \(\pi\) nach der \(n-ten\) Ziffer nach dem Dezimalpunkt" beschrieben werden.
Beispiel 3:
Die babylonische Folge (auch Folge von Heron genannt) ist rekursiv gegeben durch \[x_1=1\] und \[x_{n+1}=\frac12(x_n+\frac{2}{x_n})\] für \(n\in\mathbb{N}\). Die ersten fünf Folgenglieder der babylonischen Folge lauten:
\[ x_1 = 1 \] \[ x_2 = \frac{3}{2} = 1.5 \] \[ x_3 \approx 1.4167\] \[ x_4 \approx 1.4142\]Diese Definition ist rekursiv und gibt für großes \(n\in\mathbb{N}\) eine gute Approximation für \(\sqrt{2}\),.
Beispiel 4:
Betrachte die Folge \[1,~3,~5,~7,~9,~....\] Die explizite Formel ist gegeben durch: \[a_n = 2n-1\] für \(n\in\mathbb{N}\). Als rekursive Formel erhält man \[a_1=1, ~~a_{n+1}=a_n+2~{\rm für}~n\in\mathbb{N}.\] Die beschreibende Definition ist: "Die Folge besteht aus allen ihrer Größe nach geordneten ungeraden Zahlen, beginnend mit der kleinsten Zahl."


Übung 4.
Eine Folge \( \left( a_n \right) \) ist gegeben durch \( 2, ~3, ~5, ~7, ~11, \dots \). Gib eine Definition für diese Folge an.

Übung 5.
Die Folge \( \left( b_n \right) = \left( 1, ~2, ~4, ~8, ~16, \dots \right) \) soll auf zwei verschiedene Arten definiert werden.

2.2. Wichtige Beispiele für Folgen

Folgen bilden die Grundlage für einige zentrale Ideen in der Mathematik und können auch in anderen Gebieten wie Physik, Biologie oder Finanzwirtschaft genutzt werden, um reale Situationen zu modellieren. Wir werden fünf dieser Folgen betrachten: die arithmetische Folge, die geometrische Folge, die Fibonacci Folge, die Look-and-say sequence und Fakultäten.

Die arithmetische Folge
Es gibt viele verschiedene Definitionen der arithmetischen Folge:
Definition 1a (Arithmetische Folge)
Eine Folge \( (a_{n} \) heißt arithmetische Folge, falls die Differenz \( d \in \mathbb{R} \) zwischen zwei aufeinander folgende Folgenglieder konstant ist, d.h.:
\( a_{n+1}-a_{n}=d \text{ mit } d=const \text{und} n \in \mathbb{N}. \)
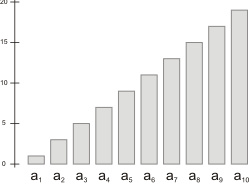
Definition 1b (Arithmetische Folge)
Eine nichtkonstante Folge \( (a_{n})_{n} \) heißt arithmetische Folge (erster Ordnung), falls die Differenzfolge erster Ordnung, also die Folge mit \( a_2 - a_1, a_3 - a_2, a_4-a_3, \ldots , \) konstant ist.
Diese Regel gibt der arithmetischen Folge ihren Namen: Das mittlere Folgenglied dreier benachbarter Folgenglieder ist das arithmetische Mittel der anderen beiden. Beispielsweise gilt
\( a_2 = \frac{a_1+a_3}{2} \text{ sowie } a_n = \frac{a_{n-1}+a_{n+1}}{2}. \)
Beispiel 1.
Die Folge der geraden natürlichen Zahlen
\( (a_n)_{n\in \mathbb{N}} = (2,4,6,8,10,12,14,16,18,\ldots) \) ist eine arithmetische Folge, da die Differenz \( d \) zwischen zwei aufeinanderfolgenden Folgengliedern stets \( d=2 \) ist.

Die geometrische Folge
Die geometrische Folge kann ebenfalls auf verschiedene Weisen definiert werden:
Definition 2 (Geometrische Folge)
Eine Folge \( (a_{n}) \) heißt geometrische Folge , falls der Quotient aus jeweils zwei benachbarten Folgengliedern konstant \( q\in\mathbb{R} \setminus \text{{0}} \) ist, d.h.
\( \frac{a_{n+1}}{a_{n}}=q \text{ für alle } n\in\mathbb{N}. \)
Bemerkung: Auf Grund von Definition 2 gilt die rekursive Beziehung \( a_{n+1} = q\cdot a_n \) für alle Folgenglieder einer geometrischen Folge. Ferner erhält man die explizite Formel
\( a_n=a_1\cdot q^{n-1} \) für das \( n-te \) Folgenglied.
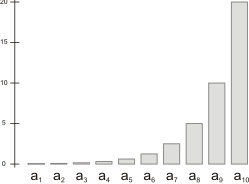
Der Name der Folge folgt wiederum aus der Definition. In diesem Fall ist das mittlere Folgenglied dreier benachbarter Folgenglieder das geometrische Mittel der beiden anderen Folgenglieder. Beispielsweise gilt:
\( a_2 = \sqrt{a_1\cdot a_3}. \)

Look-and-say Folge
Diese Folge ist auch bekannt als Conway-Folge. Sie tritt oft zu einem bestimmten Zeitpunkt des Mathematikstudiums als kniffliges Rätsel auf. Üblicher Weise lautet die Aufgabe:
Setze die nachfolgende Folge fort:
1
11
21
1211
111221
312211
Man braucht mehrere Anläufe, um die Aufgabe zu lösen, obwohl die Folge sehr einfach beschrieben werden kann:
Betrachten wir die ersten Folgenglieder:
-
"1" wird gelesen als "eine 1" \( \, \hat{=} \, \) "11"
-
"11" wird gelesen als "zwei 1en" \( \, \hat{=} \, \) "21"
-
"21" wird gelesen als "eine 2 eine 1" \( \, \hat{=} \, \) "1211"
-
"1211" wird gelesen als "eine 1 eine 2 zwei 1en" \( \, \hat{=} \, \) "111221"
-
"111221" wird gelesen als "drei 1en zwei 2en eine 1" \( \, \hat{=} \, \) "312211"
Natürlich kann die Folge mit jeder Ziffer \( d \) ( \( 0 \leq d \leq 9 \) ) gestartet werden und sieht ähnlich aus. Beispielsweise erhält man für \( d=4 \) die Folge \( 4 \) , \( 14 \) , \( 1114 \) , \( 3114 \) , \( 132114 \) , \( 1113122114 \) , ... .
Interessanterweise treten in der look-and-say Folge nur die Ziffern \( \left\lbrace 1, 2, 3 \right\rbrace \) sowie \( d \) auf, sofern die Folge mit \( d \) beginnt, da keine Ziffer öfter als dreimal wiederholt wird.

Die Fibonacci-Folge
Die Fibonacci-Folge ist sehr bekannnt, weil sie in vielen biologischen Prozessen wie dem Pflanzenwachstum eine Rolle spielt und tritt oftmals in der Natur auf. Die rekursive Definition ist:
Definition 3 (Fibonacci-Folge)
Die Fibonacci-Folge \( \left( F_k \right) \) ist durch folgende Formeln gegeben:
-
\( F_0=0 \) ;
-
\( F_1=1 \) ;
-
\( F_{k+1}=F_k+F_{k-1} \) für \( k\geq 1 \) .
Die Berechnung der ersten 15 Folgenglieder liefert \( 0 \) , \( 1 \) , \( 1 \) , \( 2 \) , \( 3 \) , \( 5 \) , \( 8 \) , \( 13 \) , \( 21 \) , \( 34 \) , \( 55 \) , \( 89 \) , \( 144 \) , \( 233 \) , \( 377 \) . Im Diagramm auf der rechten Seite sind die ersten 20 Folgenglieder dargestellt.Allerdings ist das Diagramm durchgängig bzw. kontinuierlich, wohingegen die Folge nur diskrete Zahlenwerte liefert Die absoluten Zuwächse der Folgenglieder sind zunächst relativ klein, nehmen aber sodann schnell zu.
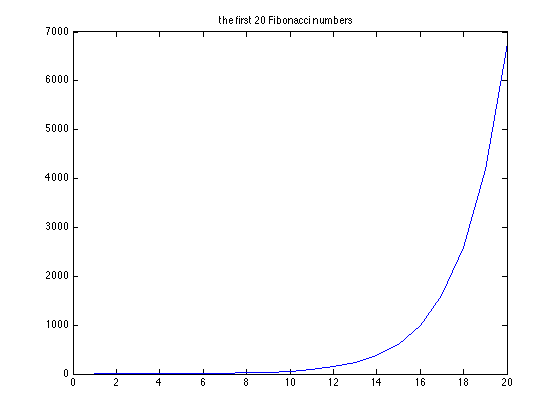

Definition von \( e \)
In kaum einem Kurs in Mathematik kommt nicht die Zahl \( e \) vor - und dieser Kurs ist keine Ausnahme. Die Zahl \( e \) kann durch \( e \approx 2.718281828459045... \) approximiert werden (zumindest russische Mathematiker verwenden folgenden Trick, um sich die Zahl \( e \) zu merken: Lew Tolstoi wurde 1828 geboren; dies sind nach dem Dezimalpunkt die Zifferngruppen 2 bis 5 und 6 bis 9 :)).
Aber woher kommt der Zahlenwert für \( e \) und weshalb hat er eine solch große Bedeutung?
Wir beginnen dabei mit einem Beispiel aus der Zinsrechnung. Angeommen man hat ein gewisses Startkapital \( K_0 \) bei einer Bank angelegt. Der Einfachheit halber nehmen wir \( K_0 = 1 \, \textrm{€} \) an. Die Bank gibt bei einer Laufzeit von einem Jahr einen (extremst utopischen aber für das Beispiel deutlich machenderen) Zinssatz von \( 100 \, \% \). Nach einem Jahr hat man dann ein Kapital \( K \) von
\( K = K_0 \cdot 2,00^1 = 2,00 \, \textrm{€}. \)
Nun verrechnet die Bank die Zinsen nicht mehr jährlich, sondern halbjährlich. Dafür werden halbjährlich \( 50 \, \% \) Zinsen berechnet. Nach einem Jahr haben wir also ein Kapital von
\( K = (1 \, \textrm{€} \cdot 1,5) \cdot 1,5 = (1,5)^2 \, \textrm{€} = 2,25 \, \textrm{€}. \)
Diesen Gedankengang wollen wir nun verallgemeinern. Wir suchen also eine Formel für eine Aufteilung in \( n \) gleichgroße Zeitintervalle. Wir müssen hierfür auch unseren Ursprungszins von \( 100 \, \% \) in \( n \) Teile aufteilen, was wegen \( 100 \, \%=1 \) dem Term \( \frac{1}{n} \) entspricht. Nach einem Jahr haben wir also ein Kapital von
\[ K = (1 + \frac{1}{n})^n. \]
Zunächst berechnen wir die ersten Folgenglieder der Folge \( (e_n) \) :
| \( e_{n} \) | \( e_{1} \) | \( e_{2} \) | \( e_{3} \) | \( e_{4} \) | \( e_{5} \) | \( e_{6} \) | \( e_{10} \) | \( e_{100} \) | \( e_{1000} \) | \( e_{10000} \) |
| 2 | 2.25 | 2.37 | 2.44 | 2.48 | 2.52 | 2.59 | 2.7 | 2.716 | 2.718 |
Die Werte der Folge \( \left( e_n \right) \) streben mit zunehmenden \( n \) gegen einen gewissen Wert. Der exakte Grenzwert dieser Folge wird mit \( e \) bezeichnet. Man wird auch mit anderen Startkapitalen oder Zinssätzen auf \( e \) stoßen. In den folgenden Abschnitten werden wir den Ausdruck Grenzwert einer Folge genauer betrachten.

Fakultäten
Betrachte die folgende rekursiv definierte Folge \( \left( f_n \right) \) :
-
\( f_1 = 1 \)
-
\( f_{n} = f_{n-1} \cdot n \) für \( n 1, n\in\mathbb{N} \)
Die ersten Folgenglieder \( \left( f_n \right) \) sind:
\( f_1 = 1, \\ f_2 = 1 \cdot 2 = 2, \\ f_3 = 1 \cdot 2 \cdot 3 = 6, \\ f_4 = 1 \cdot 2 \cdot 3 \cdot 4 = 24, \\ f_5 = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 = 120, \\ \ldots \)
Allgemein gilt \( f_n = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (n-1) \cdot n \) . Als Abkürzung benutzt man die Bezeichnung \( 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (n-1) \cdot n = n! \) und nennt sie n Fakultät.
Offensichtlich können Fakultäten rekursiv und mittels einer expliziten Formel berechnet werden. Es hängt vom jeweiligen Kontext ab, welche Formel bevorzugt werden sollte. Beispielsweise wird man beim Programmieren zunächst die rekursive Formel bevorzugt (da leichter zu programmieren), obwohl die explizite Formel effizienter ist.
Beispiel.
Die Anzahl, auf wie viele verschiedene Arten man zwei aus fünf unterscheidbaren Dingen auswählen kann, ist gegeben durch:
\( \left( \begin{matrix} n \\ k \end{matrix} \right) = \frac{n!}{k!(n-k)!} = \frac{5!}{2! \cdot (5-2)!} = \frac{5!}{2! \cdot 3!} = \)
\( = \frac{1 \cdot 2 \cdot 3 \cdot 4 \cdot 5}{1 \cdot 2 \cdot 1 \cdot 2 \cdot 3} = \frac{4 \cdot 5}{1 \cdot 2} = \frac{2 \cdot 5}{1} = 10,\text{ } k, n\in\mathbb{N}, k\leq n \)
Beispiel 2.
Gegeben sei die Folge
\( -3,~1,~5,~9,~13,~... \) Wegen \( 1-(-3) =4 \) und \( 5-1=4 \) and \( 9-5=4 \) und \( 13-9=4 \) liegt eine arithmetische Folge vor, die durch
\( a_1=-3 \) und
\( a_{n+1}=a_n+4 \) für \( n\in\mathbb{N} \) gegeben ist.
Beispiel 3.
Gegeben sei die Folge
\( 2,~6,~18,~54,~... \) Wegen \( \frac62=2 \) und \( \frac{18}{6}=3 \) sowie \( \frac{54}{18}=3 \) liegt eine geometrische Folge vor, die durch
\( a_n=2\cdot3^{n-1} \) für \( n\in\mathbb{N} \) gegeben ist.
Beispiel 4.
Es sei \( (F_k) \) die Fibonacci Folge. Berechne
\( a_k=\frac{F_{k+1}}{F_k} \) für \( k=7,8,9,10 \) und vergleiche das Resultat mit \( \frac12(\sqrt{5}+1)\approx1.6180 \) . Was könnte gelten?
Es gilt
\( F_7=13, F_8=21,F_9=34, F_{10}=55,F_{11}=89 \)
Daher gilt
\( a_7=\frac{21}{13}\approx1.6154 \), \( a_8=\frac{34}{21}\approx1.6190 \), \( a_9=\frac{55}{34}\approx1.6176 \), \( a_{10}=\frac{89}{55}\approx1.6182 \)Wir erwarten, dass \( a_k \) eine Näherung für \( \frac12(\sqrt{5}+1) \) ist.
Dies ist in der Tat der Fall und \( \frac12(\sqrt{5}+1) \) ist der sogenannte goldene Schnitt. Hier ist ein Link für weiterführende Informationen.

Übungen
Falls möglich, klassifiziere jede Folge als arithmetische Folge oder geometrische Folge und gib eine zugehörige Formel an.

Übung 1.
Gegeben sei die Folge \( \left( g_n \right) \) durch \( \left( 2, ~6, ~18, ~54, ~162, \dots \right) \) .

Übung 2.
Die Folge \( \left( h_n \right) \) ist gegeben durch

Übung 3.
Gegeben sei die Folge \( \left( p_n \right) \) durch \( \left( 2, ~5, ~10, ~13, ~26, ~29, ~58, \dots \right) \) .

2.3. Elementare Eigenschaften von Folgen

In diesem Abschnitt werden grundlegende Eigenschaften von Folgen dargelegt.

Endliche und unendliche Folgen
Wie bereits erwähnt sind der Definitionsbereich einer Folge die natürlichen Zahlen \(\mathbb{N}\). Daher ist der Definitionsbereich (abzählbar) unendlich. Man kann aber theoretisch auch nur eine (endliche) Teilmenge der natürlichen Zahlen als Definitionsmenge nutzen. Im Weiteren werden wir aber immer ganz \( \mathbb{N} \) als Definitionsmenge verwenden und uns strikt an die Definition aus 2.1 halten.
Wir betrachten kurz die nachfolgenden Beispiele:
Beispiel 1.
| \(a_{n}\) | \(a_{1}\) | \(a_{2}\) | \(a_{3}\) | \(a_{4}\) | \(a_{5}\) | \(a_{6}\) |
| -1 | 1 | -1 | 1 | -1 | 1 |
Dies ist eine Folge, die aus sechs Folgengliedern besteht und die alternierende Folge \((\pm 1)^n\) repräsentiert. Ihre Definitionsmenge ist eine endliche Teilmenge der natürlichen Zahlen. Daher heißt, die Folge \(\left( a_n \right)\) endlich.
Beispiel 2.
| \(b_{n}\) | \(b_{1}\) | \(b_{2}\) | \(b_{3}\) | \(b_{4}\) | \(\ldots\) | \(b_{n}\) | \(\ldots\) |
| -1 | 1 | -1 | 1 | \(\ldots\) | \(\left( -1 \right)^{n}\) | \(\ldots\) |
Obwohl die Folge ähnlich zu der Folge im Beispiel 1 ist, ist die Folge unendlich. Ihr Definitionsbereich ist nicht beschränkt und ist für jede natürliche Zahl definiert.
Steigende und fallende Folgen
Definition 1
Eine Folge \(\left( a_n \right)\) heißt monoton steigend, falls jedes nachfolgende Folgenglied größer oder gleich dem vorhergehenden Folgenglied ist, d.h. es gilt \(a_{n+1} \geq a_n\) für alle \(n\) aus dem Definitionsbereich der Folge.
Beispiel 3.
Betrachte die Fibonacci-Folge (hier abgekürzt mit \( (c_n) \)
|
\(c_{n}\) |
\(c_{1}\) | \(c_{2}\) | \(c_{3}\) | \(c_{4}\) | \(c_{5}\) | \(c_{6}\) |
| \(1\) | \(1\) | \(2\) | \(3\) | \(5\) | \(\ldots\) |
|
\(d_{n}\) |
\(d_{1}\) | \(d_{2}\) | \(d_{3}\) | \(d_{4}\) | \(d_{5}\) | \(d_{6}\) |
| \(-1\) | \(-\frac{1}{2}\) | \(-\frac{1}{3}\) | \(-\frac{1}{4}\) | \(-\frac{1}{5}\) | \(\ldots\) |
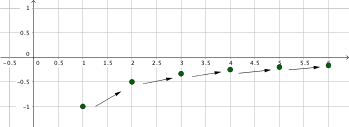
Fibonacci-Folge
Bemerkung: Die konstante Folge\(\left( 1,~ 1,~ 1,~ 1,~ 1,~ ... \right)\) ist sowohl monoton steigend als auch monoton fallend, da u.a. die Ungleichung aus Definition 1 erfüllt ist.
Um die Wiederholung von Folgengliedern zu vermeiden, wird folgender Begriff eingeführt:
Definition 2
Eine Folge \(\left( a_n \right)\) heißt streng monoton steigend, falls \(a_{n+1} > a_n\) für alle \(n\) gilt.
Monoton fallende und streng monoton fallende werden analog definiert.


Beschränkte Folgen
Um die Eigenschaften von beschränkten und unbeschränkten Folgen zu beschreiben, müssen wir nicht den Definitionsbereich, sondern den Wertebereich betrachten.
Falls eine Zahl \(M\) existiert, so dass \(a_n \leq M\) für alle \(n\) gilt, so heißt die Folge \(\left( a_n \right)\) von oben beschränkt und die Zahl \(M\) heißt obere Schranke. Analog bedeutet die Existenz einer Zahl \(N\) mit \(a_n \geq N\) für alle \(n\), dass die Folge \(\left( a_n \right)\) nach unten beschränkt ist und die Zahl \(N\) ist eine untere Schranke.#
Zusatzfrage:
Sind die Folgen der Beispiele 4.-6. monoton wachsend oder fallen?
Beispiel 4.
Die Folge der Primzahlen \(\left( 2,3,5,7,11, ... \right)\) ist eine unendliche Folge, da es unendlich viele Primzahlen gibt, und unbeschränkt, da zusätzlich jede dieser größer ist als ihr Vorgänger.
Beispiel 5.
Die Folge der ganzen Zahlen \(\left( -1,- 2,- 3,- 4,- 5, ... \right)\) ist beispielsweise nach oben beschränkt durch die Zahl \(0\), aber nicht nach unten, da jede mögliche Schranke nach unten unterschritten wird.Die Folge der geraden Zahlen \( \left( 2, 4, 6, 8, ... \right) \) ist analog nach unten durch \( 0 \), aber auch durch \( 1 \) beschränkt.
Beispiel 6.
Die Folge \(\left( -1,~ 2,~ -3,~ 4,~ -5, ..., (-1)^n \cdot n, ... \right)\) ist weder nach oben noch nach unten beschränkt. Wir können sowohl beliebig große als auch beliebig kleine Folgenglieder wählen, die größer bzw. kleiner als jede denkbare Schranke sind.

Konvergente und divergente Folgen
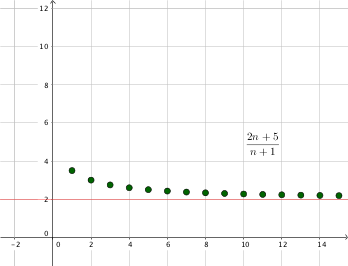
Konvergenz ist eine sehr wichtige Eigenschaft von Folgen. Wenn eine Folge konvergiert, so nähern sich die Folgenglieder einen bestimmten Wert beliebig nahe an (oder erreichen ihne). Diesen nennt man den Grenzwert der Folge (dass er existiert, wird später noch gezeigt). Beispielsweise illustriert der Graph auf der rechten Seite, dass die Folge \(a_n = \frac{2n+5}{n+1}\) gegen den Wert \(2\) konvergiert. Hierbei weichen ab einen bestimmten Index die Folgenglieder um weniger als einen beliebig kleinen, frei wählbaren Wert von \(2\) ab.
Definition 3 (konvergente Folge)
Es sei \( \left( a_n \right)\) eine Folge von reellen Zahlen. Diese heißt konvergent,
falls es eine reelle Zahl \(a\) gibt, so dass zu jeder Zahl \(\epsilon > 0\) ein \(N_{\epsilon}\) existiert mit \(\vert{ a_n - N_{\epsilon}}\vert< \epsilon\) für alle \(n \rightarrow N_{\epsilon}\). Man sagt dann, dass \(\left( a_n \right)\) gegen \(a\) konvergiert und nennt die Zahl \(a\) den
Grenzwert oder den Limes der Folge, und man schreibt
\( a= \lim\limits_{n \to \infty} a_n \)
oder
\( \left( a_n \right) \rightarrow a\) für \( n \rightarrow \infty \)
Wenn eine Folge nicht konvergent ist, dann heißt sie divergent.

Ein sehr banales Beispiel liefert die konstante Folge \(\left( 1,1,1,1, ... \right)\), die gegen \( 1 \) konvergiert. Hier stimmen Grenzwert und Wert des Folgenglieds in jedem Eintrag sogar überein. Als \( N_{epsilon} \) kann somit jedes beliebige \( N \in \mathbb{N} \) gewählt werden.
Um die Definition zu verstehen, wollen wir uns zunächst ein einfacheres Beispiel betrachten. Wir wählen hierfür \( (a_n)=\frac1n \). Die Vermutung liegt nahe, dass \( (a_n) \) gegen \(0\) konvergiert. Konvergenz kann man sich dabei so vorstellen, als ob ein Gegenspieler eine beliebig kleine positive Zahl \( \epsilon \) nennt und wir versuchen einen Index \( N_{\epsilon} \) zu finden, sodass alle folgenden Folgenglieder (\( a_n \) mit \( n \geq N_{\epsilon} \)) um weniger als \( \epsilon \) vom Grenzwert abweichen. Wir wollen dies nun für \( (a_n) \) zeigen, wie so etwas aussehen kann.

Dabei haben wir ausgenutzt, dass \( \frac1n \) stets größer-gleich 0 ist und haben \( N_{\epsilon} > \frac{1}{\epsilon} \) nach \( \epsilon \) umgeformt. Dabei fällt das entsprechende \( N_{\epsilon} \) meist vom Himmel. In diesem Beispiel war das noch gut nachvollziehbar, aber wir wollen ein weiteres Beispiel betrachten, wo dies nicht so einfach der Fall ist.
Beispiel:
Es kann bewiesen werden, dass die Folge \(a_n = \frac{2n+5}{n+1}\) aus dem Einstieg gegen \(2\) konvergiert. Dazu ziehen wir den Bruch zunächst auseinander:
\[\frac{2n+5}{n+1} = 2 + \frac{3}{n+1},\]
wobei der Summand \(\frac{3}{n+1}\) für hinreichend großes \(n\) beliebig klein wird.

Wichtig: Diese Überlegungen wollen wir aber nicht bei jeder Grenzwertbetrachtungen durchführen, da sie doch etwas aufwändiger sind. Hat man eine Folge in der in Zähler und Nenner ein Polynom (z.B. mit Variablen \( n\)) stehen, so lässt sich mit der Definition der Konvergenz zeigen:
- Ist Zählergrad < Nennergrad, dann konvergiert die Folge gegen 0
- Ist Zählergrad = Nennergrad, dann konvergiert die Folge gegen den Quotienten der Leitkoeffizienten
- Ist Zählergrad > Nennergrad, dann divergiert die Folge gegen \( +\infty \) oder \( -\infty \), je nach Vorzeichen des Leitkoeffizienten des Zählerpolynoms
Im Beispiel \( \frac1n \) ist der Zählergrad gleich 0 ("konstantes Polynom") und der Nennergrad gleich 1. Im zweiten Beispiel sind beide Grade gleich 1; der Quotient ist dann \( \frac21 = 2 \).
Ein Beispiel für eine Folge, die kein Quotient zweier Polynome ist, aber dennoch gegen \( +\infty \) divergiert, liefert die Primzahlenfolge aus Beispiel 6.

Lemma
Jede konvergente Folge ist beschränkt.

Bemerkung: Die umgekehrte Aussage, dass jede beschränkte Folge konvergent ist, ist nicht richtig. Wir betrachten hierzu die Folge \(b_n=\left( 1,~ -1,~~ 1,~ -1,~ ... \right)\): Die Folge ist beschränkt mit Schranken \(-1\) und \(1\), aber sie konvergiert nicht:
Würde sie konvergieren, so gäbe es einen Grenzwert \(A\) und für jedes \( \epsilon \) ein \( N_{\epsilon} \, (\textrm{manchmal auch} \, n_0) \in \mathbb{N} \) geben, so dass für alle \(n>n_0\) gilt: \(|b_n - A| < \epsilon\) gilt. Insbesondere auch für \( \epsilon=0,5 \). Dann könnten wir nie ein solches \(A\) und \( n_0 \) finden: Da zwischen \(1\) und \(-1\) der Abstand \(2\) liegt und wir beide unendlich oft wieder als nachfolgende Folgenglieder erhalten, können wir wegen \( \epsilon = 0,5 \) keinen Grenzwert \( A \) haben.
Beispiel 7.
Hat die Folge \((a_n)\) definiert durch \[a_n=1+(-1)^n\cdot\frac1n\] für \(n\in\mathbb{N}\) eine obere Schranke?
Wegen \[\vert(-1)^n\cdot\frac1n\vert\leq1\] für \(n\in\mathbb{N}\) ist \(2\) eine obere Schranke für die Folge. Aber es ist auch \(a_2=\frac32\) oder \(3\) eine obere Schranke für die Folge. Beachte, dass die obere und untere Schranke einer Folge nicht eindeutig ist. Eindeutig ist nur die kleinste obere und die größte untere Schranke einer Folge. In diesem Fall ist die kleinste obere Schranke \(a_2=\frac32\); eine kleinste obere bzw. größte untere Schranke muss aber kein Folgenglied sein wie die Folge \(\frac1n\) zeigt, da hier \(0\) die größte untere Schranke ist.
Beispiel 8.
Ist die Folge \[a_n=\frac{4n-4}{2n-1}\] für \(n\in\mathbb{N}\) monoton steigend oder monoton fallend? Bestimme ihren Grenzwert für \(n\to\infty\) sofern existent.
Wir haben \[a_n=2-\frac{2}{2n-1}.\] Daher ist die Folge monoton steigend, weil die Folge \((-\frac{2}{2n-1})\) monoton steigend ist. Statt dem Epsilon-Kriterium aus der Definition können wir daher auch das Verhalten für \(n\) gegen \( \infty\) untersuchen:
Da \((-\frac{2}{2n-1})\) für \(n\to\infty\) gegen \(0\) strebt (Nenner wird beliebig groß und Zähler ist konstant; der Bruch wird deshalb beliebig klein), ist der Grenzwert \(2\).
Beispiel 9.
Ist die Folge \[a_n=\frac{4n^2+n+4}{n^2+1}\] für \(n\in\mathbb{N}\) monoton steigend oder monoton fallend? Bestimme ihren Grenzwert für \(n\to\infty\) sofern existent.
Wir haben \[a_n=4+\frac{n}{n^2+1}.\] Die Folge ist monoton fallend , weil \((\frac{n}{n^2+1})\) monoton fallend ist. Der Grund hierfür ist, dass Nenner für \[n\in\mathbb{N}\] viel schneller wächst als der Zähler.
Da \((\frac{n}{n^2+1})\) für \(n\to\infty\) gegen \(0\) strebt, ist der Grenzwert \(4\).

Übung 2.
Es sei \[a_n=\frac{6n-2}{2n+2}\] für \(n\in \mathbb{N}\). Finde das kleinste \(n_0\), so dass \[\vert a_n-3\vert<\epsilon\] mit \(\epsilon =\frac{1}{100}\) für alle \(n\geq n_0\) gilt.

Übung 3.
Es sei \[a_n=\sqrt{n+1}-\sqrt{n}\] für \(n\in\mathbb{N}\). Finde den Grenzwert der Folge \((a_n)\).

Übung 4.
Finde für die Folge \( \left( f_n \right) = \left( \sqrt{3} \cdot 2^{1-n} \right) \) den Index \( n \), ab dem alle Folgenglieder kleiner als \( \frac{1}{512} \) sind.

2.4. Grenzwerte

In diesem Kapitel wollen wir den Grenzwert nochmals genauer betrachten. Wir werden feststellen, dass mit dem Grenzwert letztlich gerechnet werden kann wie mit einer Zahl.

Eindeutigkeit des Grenzwerts
Bisher haben wir recht naiv angenommen, dass eine konvergente Folgen "den" Grenzwert besitzt. Aber könnte sie nicht auch noch einen zweiten, dritten, ... oder sogar unendlich viele haben, die beliebig nah am "ersten" dran liegen? Tatsächlich ist dies nie der Fall wie wir jetzt beweisen werden. Dazu nehmen wir für eine beliebige konvergente Folge an sie hätte zwei (oder mehr) verschiedene Grenzwerte und führen dies auf einen Widerspruch bzw. unsere gewünschte Aussage zurück. Beweis: Sei \( (a_n) \) unsere konvergente Folge mit den Grenzwerten \( a \) und \( \tilde{a} \). Sei weiter \( \epsilon > 0 \) beliebig aber fest gewählt. Da es sich um jeweils zwei Grenzwerte handelt, existieren \( N_a \) und \( N_{\tilde{a}} \) mit \[\forall n \geq N_a : |a_n-a| < \frac{\epsilon}{2} \, \text{und} \, \forall n \geq N_{\tilde{a}} : \vert a_n-\tilde{a}\vert< \frac{\epsilon}{2} \] Hier sind zwei wichtige Punkte eingeflossen. Zum einen können \( N_a \) und \( N_{\tilde{a}} \) verschieden sein, da es sich um zwei verschiedene Grenzwerte handelt. Zum anderen können wir in der Ungleichung \( \frac{\epsilon}{2} \) wählen, da ein \( \epsilon \) fest gewählt ist und damit auch \( \frac{\epsilon}{2} \). Dies mag vielleicht verwirrend erscheinen, aber wenn man sich \( \frac{\epsilon}{\2} \) als \( {\epsilon}_{neu} \) vorstellt, dann erhält man letztlich wieder die Definition des Grenzwerts, die wir hier lediglich angewandt haben. Weshalb wir dies so getan haben, wird im Folgenden klarer werden. Wie beschrieben sind \( N_a \) und \( N_{\tilde{a}} \) nicht zwingend identisch. Um dennoch weiterhin beide Ungleichungen verwenden zu dürfen (Beachte je die Bedingungen \( \forall n \dots \)), sei im folgenden \( n \geq max(N_a,N_{\tilde{a}}) \). Damit erhalten wir \[ 0 \leq |a-\tilde{a} \overset{\text{Dreiecksungleichung}}{\underset{\text{}}{\leq}} |a-a_n|+|a_n-\tilde{a}|=|a_n-a|+|a_n-\tilde{a}| \overset{\text{Konvergenz-}}{\underset{\text{Voraussetzung}}{<}} \frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon \] Da wir \( \epsilon \) beliebig klein wählen können, können wir jedwede (feste) Differenz zwischen \(a\) und \( \tilde{a}\) unterbieten, was die Ungleichung verletzt, die für jedes \( \epsilon \) gilt. D.h. \( a\) und \( \tilde{a}\) müssen identisch sein und die Folge \( (a_n) \) besitzt nur einen einzigen Grenzwert. Hierbei wird auch erst wieder im letzten Schritt die Wahl von \(\frac{\epsilon}{2} \) klar - analog wie es bei der Wahl von \( N_{\epsilon}\) beim Beweis der Konvergenz der Fall war.

Rechenregeln für Grenzwerte
Nun wollen wir uns damit beschäftigen was damit passiert, welche Auswirkungen es bei einer konvergenten Folge auf den Genzwert hat, wenn wir die Folgenglieder "geschickt" verändern. Was in diesem Kontext "geschickt" bedeutet, werden wir noch herausfinden. Wir nehmen zunächst unsere bekannte konvergente Folge \( (a_n)=\frac1n \), die gegen \(0\) konvergiert. Was passiert nun beispielsweise, wenn wir zu jedem Folgenglied \( 3 \) dazu addieren? Algebraisch erhalten wir die neue Folge \( (b_n) = 3+\frac1n \), die nach Kapitel 2.3 nun gegen \( 3 \) konvergiert. Man kann sich das ganze aber auch geometrisch überlegen: Per Definition ist \( (b_n \) eine Funktion. Addieren wir zu einer Funktion eine konstante Zahl, so wird der Graph der funktion um diesen gewissen Betrag nach unten oder oben verschoben - je nach Vorzeichen der Konstanten. Damit verschiebt sich aber auch der Grenzwert um genau diesen Betrag, in unserem Fall wird aus \( 0 \) der neue Grenzwert \( 3 \). Was nehmen wir hieraus mit? Man kann bei Summen (und Differenzen) von (konvergenten) Folgen die Grenzwertbetrachtung auf die Summanden aufteilen, d.h. in unserem Fall \(\lim_{n \to \infty}(3+\frac1n)=\lim_{n \to \infty}3+\lim_{n \to \infty}\frac1n=3. In unserem Fall war eine der Folgen eine konstante Folge. Tatsächlich funktioniert dies aber für zwei beliebige konvergenten Folgen \((x_n)\) und \((y_n)\) mit den Grenzwerten \(x\) und \(y\), da diese per Definition einen Grenzwert besitzen:
Satz
Seien \((x_n)\) und \((y_n)\)zwei konvergente Folgen mit den Grenzwerten \(x\) und \(y\). Es gilt: \[ \lim_{n \to \infty}(x_n+y_n)=\lim_{n \to \infty}x_n+\lim_{n \to \infty}y_n. \]

Satz
Seien \((x_n)\) und \((y_n)\)zwei konvergente Folgen mit den Grenzwerten \(x\) und \(y\), dann konvergiert die Folge \( (x_n\cdot y_n) \) gegen \( x \cdot x \).

Sandwich-Theorem
Konvergente Folgen haben aber nicht nur die schöne Eigenschaft, dass sich die bekannten Rechenoperationen fortsetzen lassen, sondern auch, dass sich Abschätzungen vornehmen lassen wie zunächst in folgendem Lemma festgehalten wird.
Lemma
Seien \( (a_n) \) und \( (b_n \) zwei konvergente Folgen mit \( \lim_{n \to \infty} a_n = a \) und \( \lim_{n \to \infty} b_n = b \). Weiter sei \( a_n \leq b_n \) für alle \( n \in \mathbb{N} \). Dann gilt \( a \leq b \).
Ist also eine konvergente Folge durch eine weitere nach oben beschränkt, so ist dies ihr Grenzwert durch den anderen auch. Aus geometrischer Sicht macht dies durchaus Sinn, da die Werte der Folgenglieder \( (a_n) \) nicht überhalb von \( (b_n) \) liegen können (nach Voraussetzungen) und damit ihr Grenzwert \( a \) maximal \( b \) werden kann. Eine analoge Aussage gilt natürlich auch, wenn man jedes \( \leq \) durch \( \geq \) ersetzt. Auf einen Beweis verzichten wir an dieser Stelle.
Wichtig: In obigem Lemma kann das \( \leq \) nicht durch \( < \) bzw. \( \geq \) nicht durch \( < \) ersetzt werden. Hierzu betrachten wir uns die beiden Folgen \( (a_n)=0 \) und \( (b_n)=\frac1n \). Es ist bekannt, dass beide Folgen konvergent sind und offensichtlich ist \( a_n < b_n \) für alle natürlichen Zahlen \( n \). Allerdings sind beide Grenzwerte gleich \( 0 \) und insbesondere ist \( \lim_{n \to \infty} b_n = 0 \) nicht größer als \( \lim_{n \to \infty} a_n = 0 \). Mit Hilfe dieses Lemmas können wir nun eine ziemlich starke Aussage beweisen. Man stelle sich vor, dass man mit dem Fahrrad fährt und vor und hinter einem jeweils ein Bus ist, der zur Endhaltestelle fährt - man also "eingequetscht" ist. Da man weder nach vor noch nach hinten "ausbrechen" kann, bleibt einem keine Wahl als mit zur Endhaltestelle zu fahren. Mathematisch kann man die beiden Busse als Folgen betrachten, die gegen einen Grenzwert (Endhaltestelle) konvergieren. Eine dritte Folge (das Fahrrad), die zunächst nicht konvergiert (kein Ziel besitzt), konvergiert gegen denselben Grenzwert, wenn es zwischen den anderen beiden Folgen "eingequetscht" wird, also jedes Folgenglied größer- bzw. kleiner-gleich der anderen Folgenglieder ist. In der Sprache der Mathematik gilt also

Sandwich-Theorem
Seien \( (a_n) \) und \( (b_n) \) konvergente Folgen mit demselben Grenzwert \( s \). Weiter sei eine weitere Folge \( (c_n) \) gegeben mit \( a_n \leq c_n \leq b_n \) für alle \( n \in \mathbb{N} \). Dann konvergiert \( (c_n) \) und besitzt auch den Grenzwert \( s \).
Eine indirekte Anwendung für das Sandwichtheorem ist die Invervallschachtelung zur Bestimmung von \(\sqrt{2}\)
Hier können Sie das Thema Grenzwerte nochmals wiederholen und vertiefen.

Anwendung von Grenzwerten am Beispiel Heron-Verfahren
Wie die Quadratwurzel einer Zahl definiert ist, haben wir in Kapitel 1.2 rekapituliert. Doch wie berechnet man diese, wenn man nicht gerade die Wurzel aus einer Quadratzahl berechnen möchte wie z.B. \( \sqrt{3} \)? Die gängige Methode ist die Nutzung eines Taschenrechners oder eines anderen Kalkulators. Doch wie rechnet eigentlich eine solche Software, die im Wesentlichen die Grundrechenarten beherrschen? Dazu gehen wir das Problem geometrisch an. Wir hatten die Quadratwurzel vereinfacht als Umkehrung des Quadrierens wiederholt. Daher ist es naheliegend ein Quadrat mit einem gegebenen Flächeninhalt zu betrachten. Die Seitenlänge ist wegen der Flächeninhaltsformel \( A_{Quadrat}=a^2 \) für die Seitenlänge \( a \). Haben wir bspw. ein Quadrat mit Flächeninhalt \( A = 3 \) (Wir vernachlässigen Einheiten) gegeben, dann muss die Seitenlänge \( a = \sqrt{3} \) sein und wir könnten diese z.B. mit einem Zahlenstrahl ablesen. Nun ist es allerdings ziemlich schwierig ein Quadrat mit Flächeninhalt \( 3 \) zu zeichnen, da man sonst von der Seitenlänge aus ausgeht. Deshalb beginnen wir bei einem leichteren Objekt wie einem Rechteck mit Flächeninhalt \( 3 \), das wir zu einem flächeninhaltgleichen Quadrat umformen möchten. Dazu wählen wir eine Seitenlänge \( b \) beliebig, z.B. \( b_0=1 \). Da wir mehrere Seitenlängen erhalten werden, sind diese mit einem Index gekennzeichnet. Für die zweite Seite \(c_0 \) gilt (im Allgemeinen) \( A_{Rechteck}=b \cdot c \), weshalb \( c_0=\frac{3}{1}=3 \) ist. Um das Rechteck in Quadrat zu überführen, bilden wir wieder ein Rechteck, dass aber als Seitenlänge \( b_1 = \frac{b_0+c_0}{2} = 2 \) besitzt, d.h. das arithmetische Mittel aus den vorangegangenen Längen. Damit der Flächeninhalt identisch bleibt, muss dann \( c_1=\frac{3}{2}=1,5 \) gelten. Wir erkennen, dass sich die Seitenlängen nun näher angenähert haben, da wir das arithmetische Mittel gebildet haben. Damit werden wir das gewünschte Quadrat erhalten, das ja nur ein Rechteck mit zwei gleichlangen Seiten ist. Wenn wir diesen Vorgang beliebig lange wiederholen erhalten wir dann den gewünschten Wert \( b_n = c_n = 1,7320... = \sqrt{3} \) für \( n \to \infty \). Wir haben also sogar zwei verschiedene konvergente Folgen konstruiert. Einerseits die offensichtliche Folge der Seitenlänge \( b_n \) bzw. \( c_n \), die gegen den gewünschten Wert konvergiert. Aber andererseits auch die Folge der Rechtecke, die gegen das Quadrat konvergiert - Folgen und Konvergenz können also auch geometrisch geschehen und nicht nur auf der Ebene der Zahlen. Dieses Verfahren zur Berechnung von Quadratwurzeln ist übrigens schon ca. 1750 vor (!) Christus bekannt gewesen und wurde um 100 n. Chr. von Heron von Alexandria in einem Buch niedergeschieben.
2.5. Aufgaben


Aufgabe 1:
In der Abbildung rechts ist eine Eigenschaft der Fibonacci-Zahlen dargestellt. Geben Sie die Eigenschaft allgemein an und beweisen Sie sie!
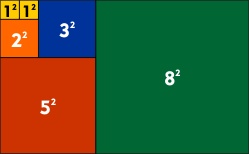
Gegeben sei ein Quadrat mit der Seitenlänge \(a\); ihm sind rote Kreise einbeschrieben (Fig. 1, Fig. 2, Fig. 3). Berechnen Sie für die Figuren jeweils den Flächeninhalt der blauen Fläche. Wie könnte man die Folge sinnvoll fortsetzen? Was ergibt sich daraus für den Flächeninhalt der blauen Fläche?
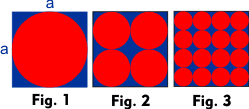
Das Quadrat in Figur 0 habe die Seitenlänge \(a\).
- Berechnen Sie den Flächeninhalt der blauen Fläche für die einzelnen Figuren.
- Die Figurenfolge werde nach dem gleichen Prinzip fortgesetzt.
Untersuchen Sie – etwa mit Hilfe eines Tabellenkalkulationsprogramms numerisch –, ob sich der Flächeninhalt einem konstanten Wert annähert.
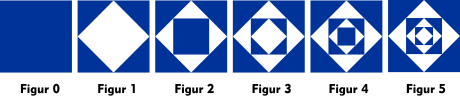

Aufgabe 4:
Gegeben ist die Folge \((a_n)_n\) mit \(a_n := \frac{n}{n+1}\)
Bestimmen Sie den Grenzwert der Folge mit der \(\varepsilon - n_0 -\)Methode.
Aufgabe 5:
Untersuchen Sie die Folgen \((a_n)_n\) und \((b_n)_n\) auf Konvergenz und bestimmen Sie ggf. ihren Grenzwert:
\(a_n := \frac{7n^5 - 2n^2 + 3}{2n^5 - 3n^2 +1}\) und \(b_n := \frac{(-1)^n n^2 + 2}{(n + 2)^2}\)
Aufgabe 6:
Zeige: Ist die Folge \((a_n)_n\) konvergent gegen \(a\), so konvergiert die Folge der Beträge \((|a_n|)_n\) gegen den Wert \(|a|\).

3. Funktionen I


Das Kapitel Funktionen I umfasst:

- Grundlagen zu Funktionen
- Eigenschaften von Funktionen
- Lineare und quadratische Funktionen
- Potenzfunktionen, Polynome und Potenzreihen
- Exponentialfunktion und Wachstum
- Trigonometrische Funktionen
- Aufgaben

3.1. Grundlagen zu Funktionen


Funktionen
In diesem Kapitel wird der Funktionsbegriff definiert und erläutert. Im Anschluss daran werden verschiedene bereits aus der Schule bekannte Funktionen eingehend betrachtet.
Was ist eine Funktion?
Isaac Newton (1643–1727) ist einer der Begründer der Differenzial- und Integralrechnung, die wir im Laufe des Kurses noch kennenlernen werden. Er untersuchte „Größen“ in geometrischen und in physikalischen Situationen, die mit der Zeit „fließen“. Mit dem Wort "fließen" meinte Newton damals, dass sich die Punkte mit der Zeit verändern. Er schreibt dazu selbst:
"Ich betrachte hier die mathematischen Größen [. . . ] durch stetige Bewegung beschrieben. [. . . ] Diese Erzeugungen finden in der Natur tatsächlich statt, und man kann sie täglich bei der Bewegung der Körper beobachten. (Newton 1704)"
Interpretiert man den Begriff Zeit abstrakter, dann entspricht das einer Größe t, die sich mit konstanter Geschwindigkeit stetig ändert und von der andere Größen x.t/, y.t/, . . . abhängt. Betrachten wir ein Beispiel zu einer Funktion:

Beispiel 1
Zwischen der in Metern pro Sekunde gemessenen Schallgeschwindigkeit \(c\) und der in Grad Celsius gemessenen Lufttemperatur \(\theta\) besteht der Zusammenhang
\(c(\theta) = 331,5 \cdot \sqrt{1 + \frac{\theta}{273} }\, \text{für } \, \theta > - 273\)
\(c\) ist eine Funktion von \(\theta\).

Definition Funktion:
Zu beliebigen Mengen \(A\) und \(B\) versteht man unter einer Funktion (bzw. Abbildung) \(f : A \rightarrow B\) eine Vorschrift, die jedem(!) \(x \in A\) genau einen Funktionswert \(y = f(x) \in B\) zuordnet. \(A\) heißt dabei Definitions- und \(B\) Zielmenge.
Für jedes \(x \in A\) heißt das dem Element \(x \) zugeordnete Element \(y \in B\) Funktionswert von \(x \). Die Menge aller Funktionswerte nennt man Wertemenge der Funktion. Mit dem maximalen Definitionsbereich einer Funktion auf einer Grundmenge bezeichnen wir alle Werte der Grundmenge in denen die Funktion wohldefiniert ist.
Der Graph von \(f\) ist die Menge \(G_f= \{(x,y) \in A × B : y = f(x)\}\)
Diese Schreibweise bedeutet, dass die Funktionsvorschrift \(f \) einem Wert \(x\) (dem „Urbild“) einen Funktionswert \(f(x)\) (das „Bild“) zuordnet. Dabei können Funktionen auch auf diskreten Mengen definiert sein, beispielsweise kann auch eine Folge als Funktion auf den natürlichen Zahlen aufgefasst werden. Eine solche Funktion nennt man diskrete Funktion.
Erklärung: Eine Funktion ist also eine eindeutige Zuordnungs-Vorschrift.
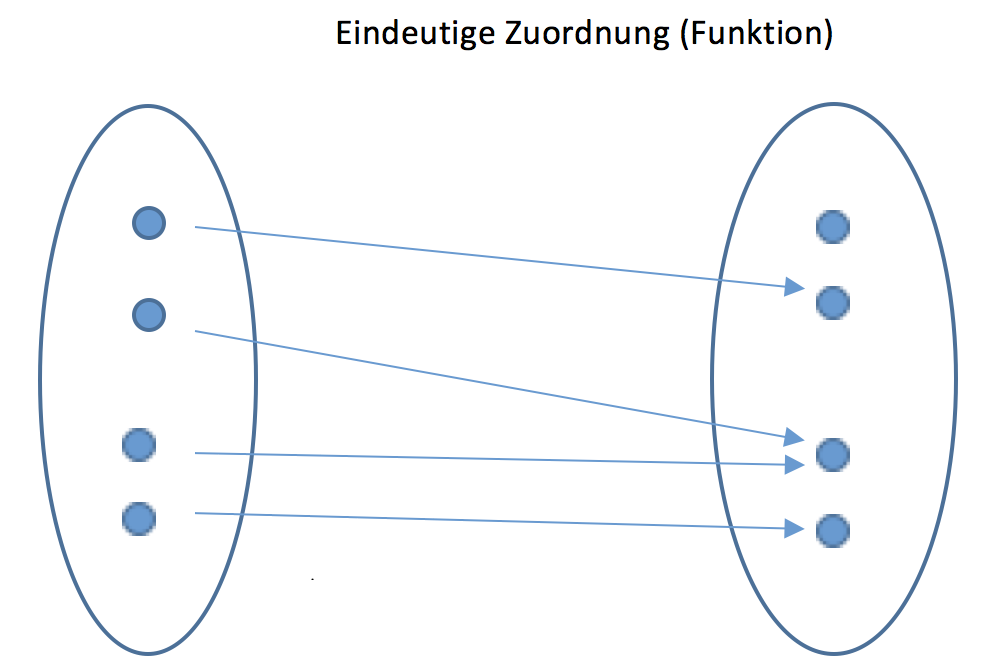
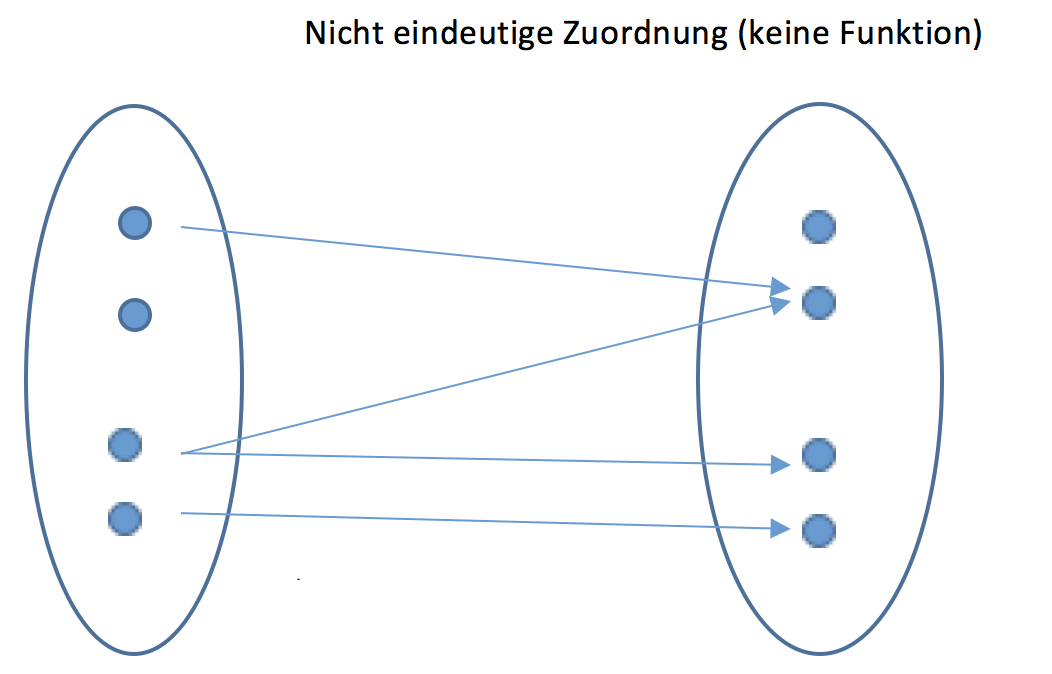
Beispiel:
In diesem Beispiel wird jeder natürlichen Zahl \(x\) ihr Quadrat \(y = f(x) = { x }^{ 2 }\) zugeordnet.
Definition 1 (Funktion)
Wenn zwei Größen so zusammenhängen, dass jedem Wert der ersten Größe genau ein Wert der zweiten Größe zugeordnet wird, dann nennt man diese Zuordnung Funktion.
Definition 2 (Funktion)
Seien A und B Mengen. Eine Zuordnung, die jedem Element der Menge A genau ein Element der Menge B zuordnet, nennt man Funktion.
Definition 3 (Funktion)
Eine Funktion f ist eine Teilmenge des kartesischen Produkts \(AxB\) zweier Mengen \(A\) und \(B\), bei der für alle \(x \in A\) genau ein \(y \in B\) existiert mit \((x, y) \in f\).

Darstellungen von Funktionen
Es gibt verschiedene Möglichkeiten eine Funktion darzustellen:
- graphische Darstellungen
- Tabellarische Darstellungen
- Darstellungen mit Termen
- verbale Darstellung, z.B. Verdopplung in 20 Minuten

Graphische Darstellungen:
Mit grafischen Darstellungen können funktionale Zusammenhänge visuell aufgezeigt werden. Im folgenden sind zwei Pfeildiagramme abgebildet. Diese stellen die Definitions- und die Zielmenge einer Funktion grafisch dar und drücken die Zuordnung von Elementen mithilfe von Pfeilen aus.
In der nebenstehenden Abbildung sehen Sie ein Pfeildiagramm zu einer Folge. In der unteren Graphik ist ein Pfeildiagramm zu Eigenschaften von Schüler:innen aufgezeigt.
Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2016). Didaktik der Analysis: Aspekte und Grundvorstellungen zentraler Begriffe. Heidelberg: Springer Spektrum, S. 54
Die gebräuchlichste grafische Darstellung von (reellen) Funktionen ist die Darstellung des Funktionsgraphen im kartesischen Koordinatensystem. Zu jedem Element \(x\) der Definitionsmenge gibt es ein Element \(y\) der Zielmenge mit \(y=f(x)\). Der Punkt \(x, y)\ liegt dann auf dem Funktionsgraphen. Beim Graphen handelt es sich, wie oben definiert, um eine Punktemenge, die die bekannte Kurven-Darstellung ergibt. Die Punkte haben die Form \((x,f(x))\).

Tabellarische Darstellungen
Eine sehr elementare Darstellung einer Funktion ist eine Wertetabelle. Diese stellt die einander zugeordneten Werte unmittelbar neben- bzw. untereinander dar. Die tabellarische Darstellungen von Funktionen hat offensichtlich Grenzen:
Wie bei Pfeildiagrammen können nur einzelne Wertepaare angegeben werden. Bei einer Funktion, die auf einer unendlichen Menge (z. B. einem Zahlenintervall) definiert ist, kann eine Tabelle also nur einen sehr kleinen Ausschnitt darstellen. Betrachtet man hier charakteristische Punkte, ist dies ein nützliches Hilfsmittel einen Graphen zu skizzieren. Darauf werden wir im nächsten Kapitel näher eingehen
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |

Darstellungen mit Termen
- Funktionsterm
\(f(x)=x^2+1\)
- Funktionsgleichung
\(y=x^2+1\)
- Zuordnungsvorschrift
\(x \mapsto x^2+1\)
Mit dem Term wird die Definitionsmenge für alle Elemente einheitlich festgelegt.

Aufgabe 1 - Darstellungswechsel:
- Ein Rechteck mit der Umfangslänge 24 cm ist x cm lang. Gib für seinen Flächeninhalt einen Funktionsterm und die Definitionsmenge an.
- Geben Sie eine Wertetabelle für \(f(x)=x^2+x \) an.
- Beschreiben Sie in Worten: \(f(t)=\frac{2t}{3}\)
Aufgabe 2:
Ergänzen Sie die folgende Tabelle:| Zahl | 3 | 11 | 27 | 64 | 89 | 111 | 127 | 567 | 625 |
| Quersummenwert | |||||||||
| Anzahl der Teiler |
Sind stellen die Zuordnungen Quersummenwert und Teilerzahl eine Funktion dar?
3.2. Eigenschaften von Funktionen


Eigenschaften von Funktionen
In diesem Kapitel beschäftigen wir uns mit grundlegenden Eigenschaften von Funktionen:
- Symmetrieeigenschaften
- Monotonie
- besondere Punkte von Funktionen: Nullstellen, Schnittstellen und Extrema

Symmetrieeigenschaften
Funktionen können symmetrisch sein. Dies bezieht sich primär auf den Graphen der Funktion und verhält sich wie schon bekannte Symmetrie. Man unterscheidet Achsensymmetrie und Punktsymmetrie.
Beispiel 1
Beispiele für Achsensymmetrie sind die Cosinusfunktion \( f(x)=cos(x) \)oder auch die Funktion \( g(x)=x² \)
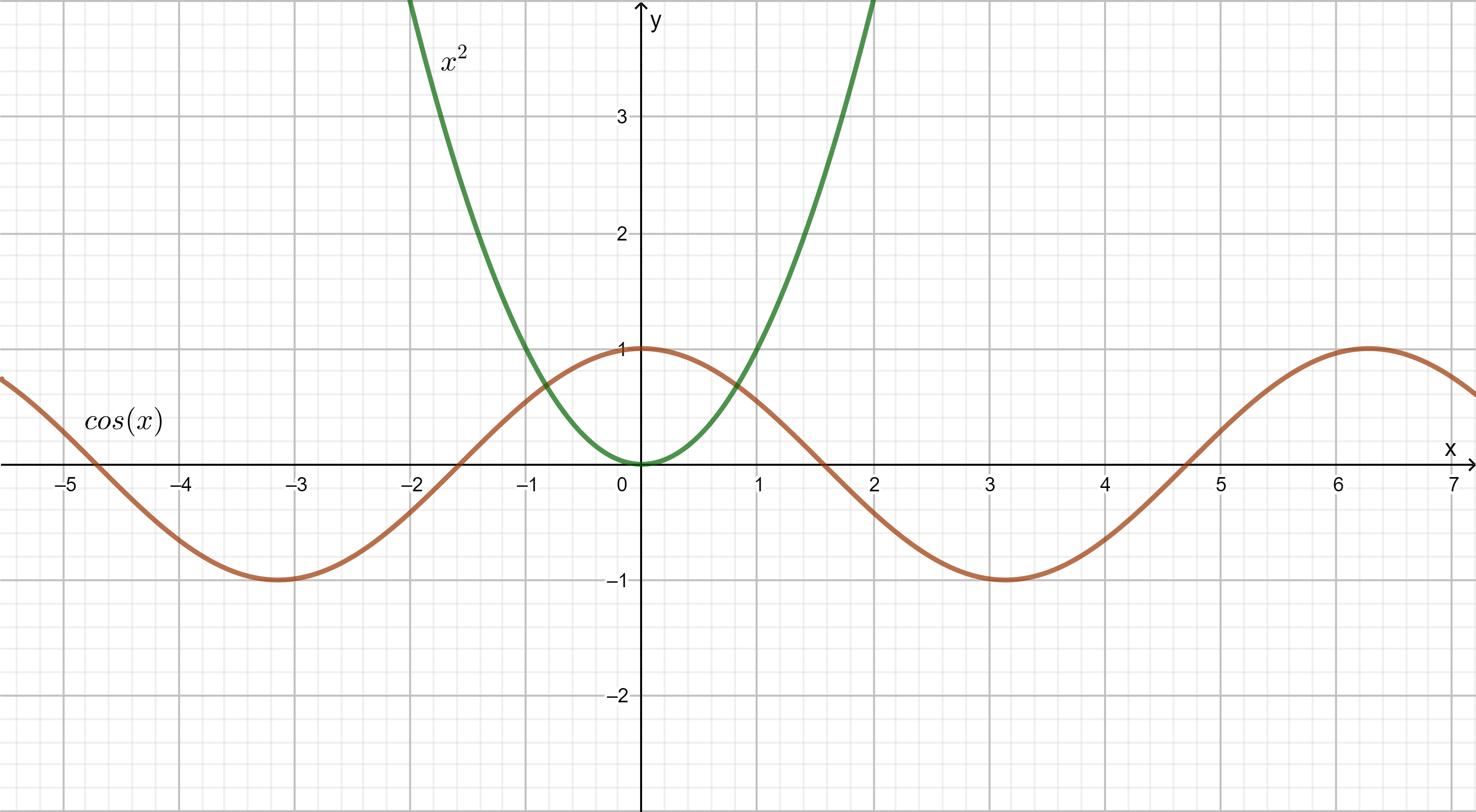

Definition Achsensymmetrie:
Eine Funktion ist achsensymmetrisch bezüglich der Gerade \( x=h \), die parallel zur y-Achse ist, wenn \( f(h-x) = f(h+x) \) für alle x-Werte aus dem Definitionsbereich erfüllt ist.
Ein Spezialfall ist \( h=0 \):
Gilt \( f(x) = f(-x) \) für alle x-Werte aus dem Definitionsbereich, wird diese Funktion ist achsensymmetrisch bezüglich der y-Achse bezeichnet.
Meist wird der Zusatz "bezüglich der y-Achse" im Spezialfall weggelassen. Spricht man von einer achsensymmetrischen Funktion ist damit für gewöhnlich die Bedingung \( f(x) = f(-x) \) für alle x-Werte aus dem Definitionsbereich gemeint.
Geometrisch interpretiert ist Achsensymmetrie bezüglich einer Geraden bedeutet, dass die Funktion an der Geraden gespiegelt ist. Alle Punkte, die jeweils gleichweit von der Geraden entfernt sind, haben den selben y-Wert.

Beispiel 2
Ein einfaches Beispiel hierfür ist \( f(x)=x \) als im Ursprung punktsymmetrische Funktion. Auch die Sinusfunktion \( g(x)=sin(x) \) ist punktsymmetrisch.

Definition Punktsymmetrie:
Eine Funktion ist punktsymmetrisch, falls \(f(a+x)-b=-(f(a-x)-b) \) für alle x-Werte erfüllt ist.
Ist sie sogar punktsymmetrisch im Ursprung, so gilt \( f(-x) = -f(x) \) .
Die Punktsymmetrie ist eine spezielle Form der Drehsymmetrie. Der Graph der Funktion ist drehsymmetrisch mit dem Drehwinkel \( 180° \). Bei der Punktsymmetrie kann man weiter differenzieren. Eine Funktion kann mit der obigen Definition punktsymmetrisch im Ursprung sein, hier gilt die Formel \( f(-x) = -f(x) \). Meistens ist Punktsymmetrie im Ursprung gemeint. Funktionen können jedoch auch punktsymmetrisch in jedem anderen Punkt \( (a/b) \) des Koordinatensystem sein. In diesem Fall gilt \( f(a+x)-b=-(f(a-x)-b) \).
Im nebenstehenden Applet können Sie Funktionen auf Punktsymmetrie im Ursprung prüfen.

Beispiel 3
Die schon bei der Achsensymmetrie betrachtete Cosinusfunktion ist nicht punktsymmetrisch im Ursprung, aber in jeder ihrer Nullstellen.
Die Funktion \( y = x^3-3x^2+2 \) ist punktsymmetrisch im Punkt \( (1/0) \) (A).

Aufgabe:
Überprüfe ob die Funktionen \( f(x) = 7x^7 - 6x^6 + 5x^5 - 4x^4 \) und \( f(x) =\frac{4}{x} \) eine Symmetrie aufweisen.

Monotonieeigenschaften
Monotonie beschreibt den groben Verlauf einer Funktion, ob sie in einem bestimmten Intervall steigt, fällt oder konstant bleibt. Man unterscheidet streng monoton steigend, monoton steigend, monoton fallend und streng monoton fallend. Weißt eine Funktion ein einheitliches Monotonieverhalten auf ihrem kompletten Definitionsbereich auf, so nennt man die Funktion (streng) monoton steigend bzw. fallend. Neben den untenstehenden Definitionen wird Monotonie oft über die Ableitung, die der Steigung der Funktion entspricht, bestimmt.Beispiel 4
Die in Beispiel 3 betrachtete Funktion \( f(x) = x^3-3x^2+2 \) weißt kein einheitliches Monotonieverhalten auf. Die Monotonie änderst sich stets an den Extrempunkten. Die Funktion wächst bis zum Punkt \((0,2)\). Im Intervall \([0,2]\) fällt die Funktion. Danach wächst die Funktion wieder.
Definition monoton wachsend:
Eine Funktion heißt auf einem Intervall I monoton wachsend, wenn für alle x-Werte dieses Intervalls mit \( x_1<x_2 \) gilt, dass \( f(x_1) \leq f(x_2) \) ist.
Definition streng monoton wachsend:
Gilt auf dem Intervall sogar \( f(x_1) < f(x_2) \) für \( x_1 < x_2 \), so ist die Funktion auf diesem streng monoton wachsend.

Beispiel 5
Die Exponentialfunktion \(e^x\), welche wir im Verlauf des Kapitels noch genauer betrachten und \( f(x)=x \) sind streng monoton wachsende Funktionen.
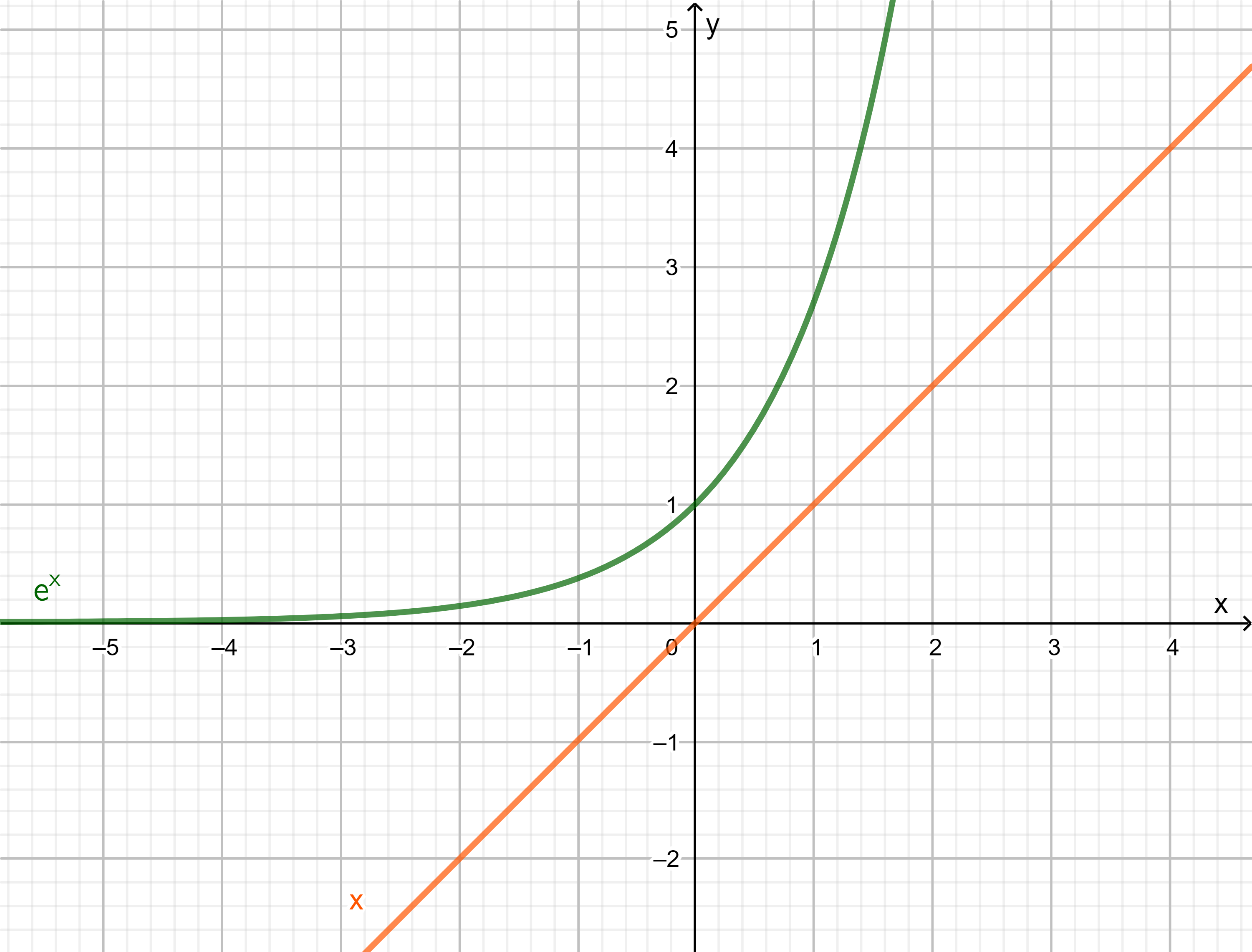

Definition monoton fallend:
Man bezeichnet eine Funktion auf einem Intervall I monoton fallend, falls für alle x-Werte \( \in I\) gilt:
\( f(x_1) \geq f(x_2) \) für \( x_1 < x_2 \)
Definition streng monoton fallend:
Man bezeichnet eine Funktion auf einem Intervall I streng monoton fallend, falls für alle x-Werte \( \in I\) gilt:
\( f(x_1) > f(x_2) \) für \( x_1 < x_2 \)
Beispiel 6
Die Funktion \( f(x) = -x^3 \) ist auf ihrem ganzen Definitionsbereich streng monoton fallend. Ihre Steigung ist zu jeder Zeit negativ und keine zwei verschiedenen y-Werte sind gleich.

Nullstellen und Schnittstellen von Funktionen
Nullstellen einer Funktion sind Punkte, in denen ihr y-Wert gleich Null ist. Die Funktion schneidet oder berührt hier somit die x-Achse. Funktionen müssen keine Nullstellen haben.
Hat mein ein Polynom mit Grad n, so besitzt dieses höchsten n Nullstellen.
Beispiel 7
Die Sinus- und Cosinusfunktion haben sehr viele Nullstellen, immer im Abstand von \(2\pi\).
Beispiel 8
Die Funktion \( f(x) = x^4 \) berührt die x-Achse im Punkt \((0/0)\). Es liegt hier eine Nullstelle vor, auch wenn die x-Achse nicht geschnitten wird.

Definition Nullstelle:
Eine Funktion \(f\) mit Definitionsbereich \(D\) hat im Punkt \( x \in D \) eine Nullstelle, falls \( f(x) = 0 \) gilt.
Um die Nullstellen einer Funktion zu ermitteln, setzt man den y-Wert gleich Null. Man erhält die Gleichung \( f(x)=0 \). Indem man den Funktionsterm für \(f(x)\) einsetzt und diese Gleichung nach \(x\) auflöst, erhält man alle Nullstellen der Funktion.
Beispiel 9
Die Funktion \( f(x) = e^x \) besitzt keine Nullstelle.
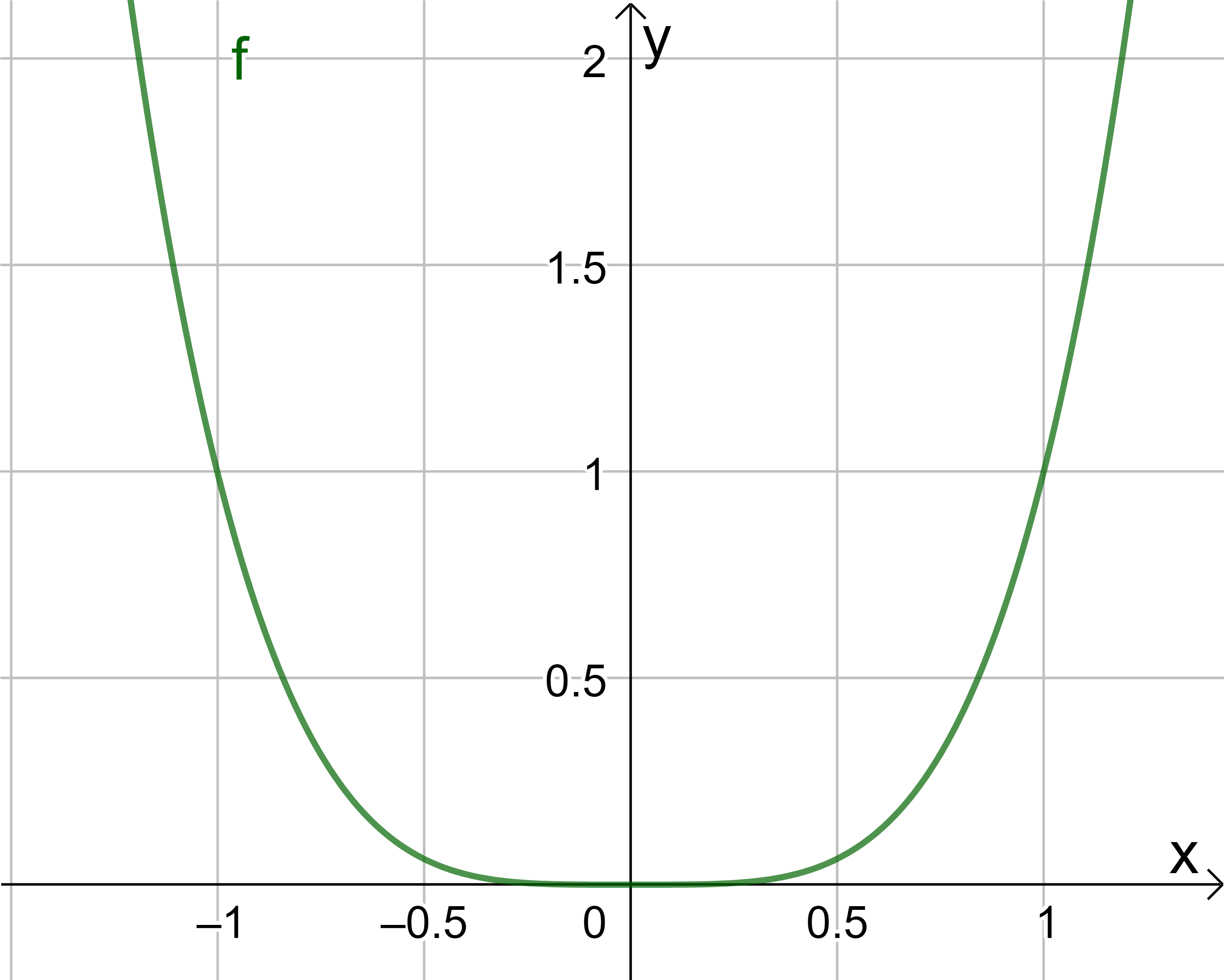

Anwenden von Nullstellen: Graphisches Lösen von Gleichungen
Eine Gleichung kann graphisch gelöst werden, indem beide Seiten der Gleichung durch einen Kurve im Koordinatensystem repräsentiert werden und man die Schnittpunkte der Kurven ausfindig macht. Wenn die Gleichung in der Form \( f(x)=0 \) geschrieben ist, können die Nullstellen in den Punkten, wo die Kurve \( y=f(x) \) die \( x \)-Achse schneidet, gefunden werden.
Graphisches Lösen ist eine annähernde Methode, wobei das algebraische Lösen benutzt wird und exakte Lösungen der Gleichung zu finden. Es gibt eine Vielzahl an Gleichungen, bei denen es zu schwer oder gar unmöglich ist sie algebraisch zu lösen, dann werden approximierende Methoden gebraucht.

Extremwerte
Bei Extremwerten einer Funktion unterscheidet man zwischen Minima und Maxima. Ein Minimum bezeichnet einen Tiefpunkt der Funktionswerte, beziehungsweise auch des Funktionsgraphen, ein Maximum hingegen stellt einen Hochpunkt der Funktionswerte, beziehungsweiße des Funktionsgraphen dar.Man unterscheidet allgemein zwischen globalen und lokalen Extrempunkten.
Bei lokalen Maxima differenziert man weiterhin zwischen strikten und nicht strikten lokalen Maxima. Analog unterscheidet man die verschiedenen Formen von Minima. Dies behandeln wir im Kapitel Funktionen II, Extremwerte genauer.
Beispiel 10
Ein striktes lokales Maximum kann man in der schon oben betrachteten Funktion \( y=x^3-3x^2+2 \) bei \( x=0 \) finden.
Auch die Sinus- und Cosinusfunktion haben viele lokale Extremwerte, jedoch keine globalen.

Definition lokales Maximum:
Ein striktes lokales Maximum in \( x \) liegt vor, wenn \( f(a) < f(x) \) für alle \( a I \) für ein bestimmtes Intervall I. Bei einem lokalen Maximum, welches nicht strikt ist, kann es sich statt einem festen Punkt \( x \) auch um ein Intervall handeln, für welches die Definition zutrifft.
Definition lokales Minimum:
Analog liegt ein striktes lokales Minimum in \( x \) vor, wenn \( f(a) > f(x) \) für alle \( a I \) für ein bestimmtes Intervall I. Bei einem lokalen Minimum, welches nicht strikt ist, kann es sich statt einem festen Punkt \( x \) auch um ein Intervall handeln, für welches die Definition zutrifft.

Beispiel 13
Bei der Funktion \( f(x)=x² \) liegt somit am Urspung \( (0/0) \) ein globales Minimum vor. Die gespiegelte Funktion \(f(x)=-x²\) weist in diesem Punkt hingegen ein globales Maximum auf.
Definition globales Maximum:
Wenn wenn \( f(a) < f(x) \) für alle \( a D \) für den kompletten Definitionsbereich D gilt, so liegt in \( x \) ein globales Maximum vor.
Definition globales Minimum:
Für ein globales Minimum in \( x \) muss gelten \( f(a) < f(x) \) für alle \( a D \) im kompletten Definitionsbereich D.
Beispiel 14
Die Funktion \( f(x)=x^3 \) hat zwar weder ein Maximum noch ein Minimum, dafür jedoch einen Terrassenpunkt.

3.3. Lineare und Quadratische Funktionen

Lineare und quadratische Funktionen
In diesem un den folgenden Kapiteln werden wir uns spezielle Funktionen anschauen. Wir beginnen zunächst mit den einfachsten Funktionen, den linearen Funktionen.
Lineare Funktionen
Die Funktionsgleichung einer linearen Funktion \(f : x \in \mathbb{R} \rightarrow f(x) \in \mathbb{R}\) lautet:
\(f(x) = m \cdot x + t \, \) mit \(\, m, \, t \in \mathbb{R}\)
\(m\) wird dabei als Steigung und \(t\) als y-Achsenabschnitt der Funktion (genauer: des Graphen der Funktion) bezeichnet.
Die Graphen linearer Funktionen sind Geraden. Bei positiver Steigung \(m > 0\) „steigt“ die Gerade, bei negativer Steigung \(m < 0\) „fällt“ die Gerade.
Diese Schreibweise bedeutet, dass die Funktionsvorschrift \(f\) einem Wert \(x\) (dem „Urbild“) einen Funktionswert \(f(x)\) (das „Bild“) zuordnet. Sowohl \(x\) als auch \(f(x)\) liegen in diesem Fall in \(\mathbb{R}\).

Je größer der Betrag von \(m\) gewählt wird, desto steiler verläuft die Gerade: Je größer eine positive Steigung ist, desto steiler verläuft sie aufwärts; je kleiner eine negative Steigung, desto steiler verläuft sie abwärts. Analog dazu wird die Gerade für kleinere positive \(m\), bzw. für größere negative \(m\) flacher.
Für \(m=0\) ergibt sich der Sonderfall einer Gerade, die parallel zur \(x\)-Achse, also waagrecht, verläuft:
\(f(x) = t\)
Man sollte jedoch beachten, dass mit der linearen Funktion keine Geraden dargestellt werden können, die parallel zur y-Achse verlaufen.
Der Betrag \(|a|\) einer Zahl \(a\) ist deren „Absolutwert“, also ihr Wert „ohne Vorzeichen“: \(|3|=3, |-3|=3\)
Entsprechend kann die Betragsfunktion
\(f(x)=|x|=\begin{cases} x, \text{für } x\geq 0\\ -x, \text{für } x < 0\end{cases}\)
definiert werden:

Aufgabe: Überlegen Sie, warum dies nicht möglich ist!
Derartige Geraden können hingegen mit der folgenden Gleichung (dies ist KEINE Funktionsgleichung!) dargestellt werden:
\(\{(x, y)|x=a, a\in \mathbb{R}\}\)
Da \(t\) unabhängig von \(x\) (\(t\) verändert sich also nicht für verschiedene \(x\)-Werte/ ist für alle \(x\) gleich.) den Funktionswert erhöht oder erniedrigt, kann man durch \(t\) den gesamten Graphen an der \(y\)-Achse entlang verschieben. Für positives \(t\) wird der Graph nach oben und für negatives \(t\) nach unten verschoben. Ist \(t=0\), so verläuft die Gerade durch den Ursprung; es gilt nämlich:
\(f(0)=m\cdot 0+t=t=0\).
Man spricht entsprechend von einer Ursprungsgerade.


Berechnung der Steigung und des y-Achsenabschnitts
Die Steigung einer linearen Funktion berechnet sich mit Hilfe des Steigungsdreiecks wie folgt:
\(m = \frac{\Delta y}{\Delta x} = \frac{\Delta f(x)}{\Delta x} = \frac{f(x_2) - f(x_1)}{x_2 - x_1} \)
Dabei wird der vertikale Abstand zweier Punkte des Graphen durch den horizontalen Abstand der beiden Punkte geteilt (genauer gesagt, die Werte der jeweiligen Abstände). Die Steigung gibt also an, um welchen Wert sich die Funktion vertikal ändert, wenn horizontal eine gewisse Änderung erfolgt.
Ähnlich wird bspw. bei Steigungen im Straßenverkehr verfahren. Es wird gemessen, um wie viele Höhenmeter sich ein Fahrzeug nach oben bewegt, während es sich 100m in der Waagrechten fortbewegt. (Die tatsächlich zurückgelegte Strecke stellt dann die Hypotenuse des entstehenden rechtwinkligen Dreiecks dar.) Auf Grund dieser Idee – \(x\) Höhenmeter pro 100m in der Ebene – wird die entsprechende Steigung in Prozent („pro Hundert“) angegeben.

Der y-Achsenabschnitt \(t\) ist der Wert der Funktion bei \(x=0\), der sich berechnen lässt, indem \(0\) in die Funktionsvorschrift eingesetzt wird:
\(t = f(0)\)
How to - Zeichnen des Funktionsgraphen
Zum Zeichnen des Funktionsgraphen sollte man sich folgende Vorgehensweise einprägen:
- Vom Ursprung aus um \(t\) an der \(y\)-Achse „entlanggehen“. Wir nennen diesen Punkt \(P\).
- Von \(P\) aus um den Wert des Zählers von \(m\) (s. Steigungsdreieck) nach oben und um den Wert des Nenners von \(m\) nach rechts gehen. Wir nennen diesen Punkt \(Q\).
- Der Graph ist eine Gerade durch \(P\) und \(Q\).
Ist \(m\) bereits berechnet worden, so lässt sich als Zähler in obiger Vorgehensweise \(m\) verwenden, als Nenner 1, denn es gilt: \(m = \frac{m}{1}\)
Berechnung des Winkels zwischen Gerade und x-Achse
Wir betrachten das rechtwinkelige Steigungsdreieck. Mit Hilfe der Definition für die Winkelfunktion Tangens im rechtwinkligen Dreieck ((Länge der) „Gegenkathete geteilt durch (Länge der) Ankathete“) gilt:
\(tan(\alpha ) = \frac{\Delta f(x)}{\Delta x} = m\)
nach Definition der Steigung \(m\) und damit
\( \alpha = arctan(m)\)

Nullstellen von linearen Funktionen
Eine lineare Funktion hat genau eine Nullstelle ( \(f(x)=0\) ), also genau einen Schnittpunkt mit der \(x\)-Achse.
Ausgenommen ist der Sonderfall \(m=0\). Damit wäre \(f\) eine konstante Funktion und ihr Graph eine Parallele zur \(x\)-Achse: \(f(x)=t\). Eine solche Funktion hat keine Nullstellen für \(t \neq 0\). Für \(t = 0\) gilt: \(f(x)=0\). In diesem Fall hat die Funktion ausschließlich (und damit unendlich viele) Nullstellen.
Zur Berechnung der Nullstelle \(x_0\) setzt man \(f(x_0)=m\cdot x_0+t = 0\) und löst diese Gleichung nach \(x_0\) auf:
\(x_0 = - \frac{t}{m}\)

Beziehungen zwischen den Graphen zweier linearen Funktion
Die Funktionsgraphen einer linearen Funktion sind genau dann parallel, wenn ihre Steigung gleich ist:
\(m_1 = m_2 \Leftrightarrow G_f \parallel G_g\)
Parallele Geraden \(f_1, f_2, f_3,\ldots \) unterscheiden sich also nur durch ihre \(y\)-Achsenabschnitte \(t_1, t_2, t_3,\ldots \) Sie gehen also durch Parallel-Verschiebungen in vertikaler Richtung (nach oben und nach unten) auseinander hervor.
Zwei Geraden \(f=m_1x+t_1\) und \(g=m_2x+t_2\) stehen genau dann aufeinander senkrecht, wenn das Produkt der beiden Steigungen \(-1\) ergibt:
\(m_1 \cdot m_2 = - 1 \Leftrightarrow G_f \bot G_g\)
\(G_f\) bezeichnet den Funktionsgraphen der Funktion \(f\).

Aufgabe:
Begründen Sie diesen Zusammenhang zwischen \(m_1\) und \(m_2\) (siehe vorhergehender Text).

Quadratische Funktionen
Die allgemeine Form der quadratischen Funktion \(f : x \rightarrow f(x)\) lautet:
\(f(x) = a \cdot x^2 + b \cdot x + c \, \) mit \( \, a, \,b, \,c \in \mathbb{R}\)
Die Graphen quadratischer Funktionen sind Parabeln. Der Koeffizient („Vorfaktor“) von \(x^2\), also \(a\), bestimmt die Form der Parabel. Bei einem positivem Wert von \(a\) ist die Parabel nach oben, bei einem negativen Wert nach unten geöffnet. Je größer \(|a|\) gewählt wird, desto "enger" wird die Parabel. Analog wird die Form der Parabel für kleineres \(|a|\) weiter. Eine Veränderung des Parameter \(c\) bewirkt eine Verschiebung der Parabel in y-Richtung, denn \(c\) ist unabhängig von \(x\). Veränderungen in \(x\) bewirken also keine Veränderungen in \(c\).
Wird \(c\) um eins erhöht, dann wird der Graph um eine Einheit nach oben verschoben. Wird \(c\) um eins verringert, wird der Graph dagegen um eine Einheit nach unten verschoben.
\(c\) entspricht also sozusagen dem \(y\)-Achsenabschnitt, den wir von den Geraden kennen.
\(|a|\) bezeichnet den Betrag, bzw. Absolutwert von \(a\), also den Wert von \(a\) „ohne negatives Vorzeichen“
\(f(x)=|x|=\begin{cases} x, \text{für } x\geq 0\\ -x, \text{für } x < 0\end{cases}\)
Scheitelpunktsbestimmung
Der Scheitelpunkt der Parabel ist entweder das absolute Minimum (falls \(a\) positiv ist) oder das absolute Maximum (wenn \(a\) negativ ist). Die Koordinaten des Scheitelpunkts lassen sich direkt ablesen, wenn der Funktionsterm mittels quadratischer Ergänzung unter Ausnutzung der binomischen Formeln in die Scheitelpunktsform umgeformt wird:
\(f(x) = a \cdot (x - x_S)^2 + y_S\)
Als „absolut“ (oder „global“) wird ein Extremum (Maximum oder Minimum) bezeichnet, wenn es sich dabei um den größten/ kleinsten Wert im gesamten Definitionsbereich handelt. Im Gegensatz dazu ist ein „lokales“ Maximum/ Minimum nur Maximum/ Minimum in einer bestimmten Umgebung.
Der Koeffizient \(a\) ändert sich bei der Umformung nicht!

Aufgabe:
Zeigen Sie, wie die allgemeine Form \(f(x) = ax^2+ bx + c,\text{ }a, b, c\in\mathbb{R}, a\neq 0\) in die Scheitelpunktform \(f(x) = a \cdot (x - x_S)^2+ y_S\) überführt werden kann.

Bei dieser Form der Funktionsgleichung lässt sich der Graph von \(f\) als Variation der Normalparabel mit Gleichung \(g(x) = x^2\) interpretieren.
\(f\) entsteht aus dieser durch Verschiebung um \(x_s\) nach rechts, um \(y_s\) nach oben und durch Streckung/Stauchung um den Faktor \(a\).
Mit den Koeffizienten der allgemeinen Form für quadratische Gleichungen (s. oben) ergeben sich die Koordinaten des Scheitelpunkts dann zu:
\(x_s = -\frac{b}{2a}\)
\(y_s = \frac{4ac - b^2}{4a}\)
Der Scheitelpunkt hat dann die Koordinaten \(S(x_s|y_s)\). Der Graph von \(f\) ist achsensymmetrisch zu einer Parallelen zur \(y\)-Achse durch \(x_s\).

Nullstellen einer quadratischen Funktion
Eine quadratische Funktion hat je nach Lage des Scheitelpunktes \(S\) und dem Vorzeichen von \(a\) keine, eine oder zwei Nullstellen.
Zur Berechnung der Nullstellen setzt man \(f(x) = 0\) und löst die Gleichung mittels der quadratischen Lösungsformel, der sogenannten Mitternachtsformel:
\(x_{1,2} = \frac{1}{2a} (-b \pm \sqrt{b^2 - 4ac})\)

Aufgabe
Zeigen Sie, warum die Formel gültig ist!
\(x_{1,2} = \frac{1}{2a} (-b \pm \sqrt{b^2 - 4ac})\)
Der Bereich unter der Wurzel wird als Diskriminante bezeichnet, finden Sie einen Zusammenhang zwischen Diskriminante und Anzahl der Nullstellen!
Beispiel 1.
Die Gleichung \[ 2x^2+3x=0 \] kann durch Anwenden des Satzes vom Nullprodukt gelöst werden: Ausklammern des gemeinsamen Faktors \( x \) liefert \[ x(2x+3)=0 \] und somit sind die Nullstellen \[ x=0 \textrm{ and } x=-\frac{3}{2}. \]
Beispiel 2.
Wenden wir die Lösungsformel für quadratische Gleichungen auf die Gleichung \[ 2x^2-7x+6=0. \] Die Formel liefert \[ x= \frac{7 \pm \sqrt{(-7)^2 - 4\cdot 2 \cdot 6}}{2\cdot 2} = \frac{7 \pm 1}{4}. \] Also sind die Nullstellen \[ x_1 = 2 \textrm{ and } x_2 = \frac{3}{2}. \]
Beispiel 3.
Wenn die quadratische Formel auf die Gleichung \[ x^2+2x+2=0, \] angewandt wird, ist eine negative Zahl \( 2^2-4\cdot 1 \cdot 2 = -4\) die Diskriminante (unter der Wurzel). Somit hat die Gleichung keine reellen Lösungen.
Geometrisch sind die Lösungen einer quadratischen Gleichung die Punkte, bei denen die Parabel \( y=ax^2+bx+c \) die \(x\)-Achse schneidet. . In dem Fall, in dem keine reellen Lösungen existieren, gibt es keine solchen Schnittpunkte. Im unteren Schaubild können die Werte der Parameter \(a\), \(b\) und \(c\) verändert werden, um verschiedenen Situationen zu veranschaulichen.

Aufgabe 1:
Berechnen Sie die Nullstellen der Funktion \(f\) und zeichnen Sie den Funktionsgraphen für \(f(x) = -3x + 6\).
Aufgabe 2:
Gegeben sind zwei Punkte \(P = (4|3)\) und \(Q = (0|-2)\). Bilden Sie die Gleichung der Geraden \(g\) durch \(P\) und \(Q\) und berechnen Sie den Winkel, den \(g\) mit der x-Achse einschließt!
Aufgabe 3:
Bestimmen Sie durch quadratische Ergänzung den Scheitelpunkt \(S\) der Parabel mit \(f(x) = -5x^2+ 30x + 47\).
Aufgabe 4:
Berechnen Sie die Nullstellen folgender Parabel mit \(f(x) = -\frac{1}{2} x^2 + \frac{1}{2} x + 3\).

3.4. Potenzen und Wurzeln


In diesem Kapitel wiederholen wir zunächst die Eigenschaften von Potenzfunktionen und Polynomen. In einem freiwilligen Exkurs führen wir dann noch ein wichtiges Konzept der Analysis ein - die Potenzreihen.
Potenzfunktionen

Eine Potenzfunktion mit natürlichem Exponenten ist eine Funktion der Form:
\(f : \mathbb{R} \rightarrow \mathbb{R}^{+}, x \mapsto a \cdot x^n\) mit festem \(a > 0, n \in \mathbb{N} \)
\(n=1,2,3,\cdots \)
Zwei Spezialfälle einer Potenzfunktion sind uns bereits aus dem letzten Kapitel bekannt:
Für \(n=1\) ergibt sich die lineare Funktion \(f\) mit \(f(x) = ax\) und für \(n=2\) ergibt sich die reinquadratische Funktion \(f\) mit \(f(x) = ax^2\).

Variieren Sie bei folgendem Beispiel für \(f(x) = a \cdot x^3\) den Parameter \(a\). Erläutern Sie die Veränderung des Graphen.

Eine Potenzfunktion mit ganzzahligem Exponenten ist eine Funktion der Form:
\(f : \mathbb{R}\backslash\{0\} \rightarrow \mathbb{R}, x \mapsto a \cdot x^z\) mit festem \(a > 0, z \in \mathbb{Z}\)
\(z=\cdots ,-2,-1,0,1,2,\cdots \)
Die Potenzfunktionen mit ganzzahligem Exponenten lassen sich in zwei Gruppen mit unterschiedlichen Eigenschaften teilen:
\(f(x) = a \cdot x^n\) (natürlicher Exponent, \(n>0\)):
Diese Funktionen haben stets eine Nullstelle für \(x = 0\) und für betragsmäßig "große" \(x\) streben ihre Funktionswerte gegen plus oder minus unendlich. Ihre Graphen nennt man Parabeln \(n\)-ter Ordnung.
\(f(x) = a \cdot x^{-n} = a \cdot \frac{1}{x^n}\) (negativer natürlicher Exponent, \(-n<0\)):
Diese Funktionen haben stets eine Polstelle bei \(x = 0\), d.h. für betragsmäßig "kleine" \(x\) streben die Funktionswerte gegen plus oder minus unendlich. Der Wert \( f(0) \) ist nicht definiert, da durch 0 teilen nicht definiert ist, weshalb die Null in Definition 2 im Definitionsbereich ausgeschlossen ist. Für betragsmäßig "große" \(x\) gehen die Funktionswerte gegen 0.
Sie haben aufgrund der Polstelle zwei Äste, siehe hierfür untenstehendes Applet.
Die Graphen von Potenzfunktionen mit ungeradem Exponent sind punktsymmetrisch zum Ursprung, die von Potenzfunktionen mit geradem Exponent sind achsensymmetrisch zur y-Achse, exemplarisch gilt:
\(f(-x) = (-x)^2 = x^2 = f(x)\)
\(f(-x) = (-x)^3 = -(x^3) = -f(x)\)
Für wachsende \(x\) wird der Betrag von \(x^n\) immer größer und \(f(x)\) strebt deshalb gegen \(\infty\) bzw. \( - \infty\)
\(x^{-n} = \frac{1}{x^n}\)
Für wachsende \(x\) wird der Nenner des Bruchs (bzw. eigentlich sein Betrag!) immer größer und der Gesamtbruch sowie \(f(x)\) streben deshalb gegen 0.

Eine Potenzfunktion mit Stammbruch im Exponenten ist eine Funktion der Form:
\(f : \mathbb{R}_0^+ \rightarrow \mathbb{R}_0^+, x \mapsto a \cdot x^{\frac{1}{n}}\) mit festem \(a >0, n \in \mathbb{N}\)
Stammbrüche:
\(\frac{1}{n} = 1,\frac{1}{2},\frac{1}{3},\ldots \)

Unten sehen Sie den Graphen der Funktion \(f\) mit \(f(x) = x^{\frac{1}{n}}\) für \(n \in \{2, 3, 4, 5, 6\}\). Beschreiben Sie den Graphen und achten Sie dabei auf Definitionsbereich, Monotonie, größte und kleinste Funktionswerte. Gibt es Punkte, die allen Graphen dieser Bauart gemeinsam sind? Begründen Sie!
Insbesondere ist die Funktion
\(f: \mathbb{R}_0^+ \rightarrow \mathbb{R}_0^+, x \mapsto \sqrt{x} = x^{\frac{1}{2}}\),
die jeder positiven Zahl ihre Quadratwurzel zuordnet, eine Potenzfunktion. Analog sind auch die k-ten Wurzeln \( \sqrt[k]{x}\) Potenzfunktionen nach der Festlegung \(\sqrt[k]{x} = x^{\frac{1}{k}}\) (vgl. dazu Kapitel 1.3). Die k-te Wurzelfunktion \(f\) mit \(f(x) = x^{\frac{1}{k}} \) ist also die Umkehrfunktion zur Potenzfunktion \(g\) mit \(g(x) = x^k\) auf dem Intervall \( \mathbb{R}_0^+ \) und \(g\) ist die Umkehrfunktion zu \(f\).

Eine Potenzfunktion mit negativem Stammbruch im Exponenten ist eine Funktion der Form:
\(f : \mathbb{R}^+ \rightarrow \mathbb{R}^+, x \mapsto a \cdot x^{ - \frac{1}{n}}\) mit festem \(a > 0, n \in \mathbb{N}\)
Für ungerades \( n \) kann der Definitionsbereich zu \( \mathbb{R}\setminus\{0\} \) erweitert werden.

Vergleichen Sie die Graphen der Funktionen mit negativen Stammbrüchen im Exponenten (blau) mit den bereits bekannten Graphen der Funktionen mit poitiven Stammbrüchen im Exponenten (rot gestrichelt). Achten Sie dabei auf Symmetrie, Monotonie, größte und kleinste Funktionswerte. Gibt es Punkte, die allen Graphen gemeinsam sind? Begründen Sie.

Eine Potenzfunktion mit rationalem Exponenten ist eine Funktion der Form:
\(f : \mathbb{R}^+ \rightarrow \mathbb{R}^+, x \mapsto a \cdot x^{\frac{p}{q}}\) mit festem \(a > 0, p \in \mathbb{Z}, q \in \mathbb{N}\)
Je nach Vorzeichen und Wert des Zählers sowie Nenners des Exponenten \( \frac{p}{q} \), kann der Definitionsbereich erweitert werden.
\(x^{\frac{p}{q}} = \sqrt[q]{x^p} \)

Vergleichen Sie den Graphen der Potenzfunktionen mit rationalem Exponenten (blau) mit dem, den Sie schon aus den obigen Abschnitten kennen (rot und lila gestrichelt); mit dem Schieberegler können Sie dazu wieder die Exponenten verändern. Beschreiben Sie Gemeinsamkeiten und Unterschiede der Graphen! Achten Sie dabei auf Definitionsbereich und Symmetrie.
Die Darstellung von Funktionen der Form \(f(x) = (\sqrt[k]{x})^p\) als \(f(x) = x^{\frac{p}{k}}\) spielt vor allem beim Ableiten von Funktionen eine Rolle, da sich die bekannten Ableitungsregeln damit auch auf Wurzel-Funktionen übertragen lassen.
Polynome werden aus den Potenzfunktionen \(ax^n\) ("Monome") mit natürlichem \(n\) mittels Addition und Subtraktion gebildet. Sie sind auf ganz \(\mathbb{R}\) definiert.

Zu \(a_0, a_1, \ldots, a_n \in \mathbb{R}\) heißt
\(p: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \sum_{k=0}^n {a_k x^k} = a_0 + a_1 x + a_2 x^2 + \ldots + a_n x^n\)
Polynom vom Grad \(n\), falls \(a_n \ne 0\). Man nennt es normiert, falls \( a_n=1 \) gilt.
Der Grad eines Polynoms gibt also den größten Exponenten aller auftretender Monome an. Für gewöhnlich ordnet man die Summanden absteigend nach Größe der Exponenten.
Nach Definition sind bswp. konstante, lineare, quadratische und Potenzfunktionen Polynome.
Die Graphen der Polynome mit Grad \(>2\) besitzen ein nicht mehr so leicht bestimmbares Verhalten und Aussehen wie die Spezialfälle der Graphen konstanter, linearer und quadratischer Funktionen. Um die Eigenschaften dieser Polynome und deren Graphen zu bestimmen, wendet man das aus der Schule bekannte Verfahren der Kurvendiskussion an, diese wird in Kapitel "Differentialrechnung" ausfühlich behandelt.
Polynome, bei denen nur gerade Exponenten bei den Monomen auftreten, sind achsensymmetrisch zur y-Achse; Polynome, bei denen nur ungerade Exponenten bei den Monomen auftreten, sind punktsymmetrisch zum Ursprung.
Polynome sind in der Analysis von großer Bedeutung, da sie eine (relativ) einfache Funktionenklasse darstellen. Insbesondere sind sie leicht zu differenzieren und integrieren. Darüber hinaus gibt es viele Möglichkeiten komplizierte Funktionen durch Polynome anzunähern.
Nullstellen von Polynomen
Von besonderer Bedeutung in der Analysis sind die Nullstellen von Polynomen \( p \), d.h. diejenigen Werte \( x \) für die \( p(x)=0 \) gilt. Sie werden spätestens in der Kurvendiskussion wieder auftauchen. Nach dem Fundamentalsatz der Algebra besitzt ein Polynom vom Grad \( n \) auch \( n \)-viele komplexe Nullstellen. Wichtig ist hierbei, dass diese komplex sein können. So hat das Polynom \( x^2 + 1 \) keinerlei reelle Nullstellen, aber die zwei komplexen Nullstellen \( i \) und \( -i \). Interessant ist, dass komplexe Nullstellen immer paarweise auftauchen, da auch das komplex konjugierte stets wieder eine Nullstelle ist (vgl. hier \( i \) und \( -i \)).
In diesem Kurs werden wir aber hauptsächlich Polynome betrachten, die nur reelle Nullstellen besitzen. Diese kann man dann auch in einer faktorisierten Form darstellen, d.h. \( p(x)=a \cdot (x-x_1)\cdot (x-x_2) \cdot \dots \cdot (x-x_n) \) mit \( a \in \mathbb{R} \setminus \{0\} \) und den \(n\) Nullstellen \(x_1,x_2, \dots \). Der Koeffizient \( a_n \) und \( a \) stimmen dabei überein. Beachte außerdem, dass die Nullstellen nicht zwingend verschieden sein müssen. Man spricht je nach Häufigkeit dann von doppelten, dreifachen, etc. Nullstellen.
Für gewöhnlich sind Polynome aber nicht in dieser Form dargestellt und wir müssen zunächst die Nullstellen finden. Für Polynome vom Grad 1 und 2 (Geraden und Quadratischen Funktionen) sind uns schon Lösungsalgorithmen bekannt. Für Polynome vom Grad 3 und 4 existieren zwar Formeln für die Nullstellen, diese sind aber recht komplex und zu empfehlen auswendig zu lernen. Für Polynome vom Grad 5 und höher kann man mit Mitteln der Hochschulalgebra zeigen, dass es keine allgemeine Lösungsformel geben kann, sondern lediglich in Spezialfällen. Wir benötigen also eine andere Herangehensweise.
Polynomdivision
Wir gehen zunächst von einem einfachen Beispiel ausgehen, wo wir eine Nullstelle kennen. Sei \( f(x)=x^3-6x^2-x+6 \). Durch Raten hat man bspw. die Nullstelle \( x_1 = 1 \) herausgefunden, d.h. einer der Faktoren aus unserer Faktorisierung ist \( (x-1) \). Da wir aus einem Produkt die weiteren Faktoren herausfinden wollen und schon einen Faktor kennen, können wir mittels Division vorgehen. Wir gehen dabei wie bei der schriftlichen Division vor:
Zunächst werden sowohl Dividend als auch Divisor der Größe der Exponenten nach sortiert und aufgeschrieben. Da der größte Exponent in \( (x-1) \) das Monom \( x \) ist, teilen wir wiederum \( x^3 \) aus \( x^3-6x^2-x+6 \) durch \( x \) und erhalten als ersten Summanden des Ergebnisses \( x^2 \). Um nun fortzufahren, wird \( x^2 \) mit \( (x-1) \) multipliziert und das Ergebnis \( (x^3-x^2) \) von \( x^3-6x^2-x+6 \) abgezogen. Dies wird schriftlich getan, indem es unter den Ausdruck geschrieben wird.
Wir erhalten \( -5x^2-x+6 \), wobei man das \( +6 \) oben stehen lässt, da es erst im nächsten Schritt relevant ist. Nun beginnen wir von vorn: Wir teilen den ersten Summanden durch \( x \) und erhalten \( - 5x^2 \). Dies wird mit \( (x-1) \) multipliziert und von \( -5x^2-x+6 \) abgezogen. Wir berechnen also \( (-5x^2-x+6)-(-5x^2+5x) \) und erhalten \( -6x+6 \).
Im letzten Schritt teilen wir wieder den ersten Summanden durch \( x \), erhalten \( -6 \), multiplizieren dies mit \( (x-1) \), ziehen das Ergebnis von \( -6x+6 \) ab und bekommen als Ergebnis \( 0 \), d.h. unsere Polynomdivision ging auf. Unser Ergebnis lautet nun \( (x^3-6x^2-x+6):(x-1)=x^2-5x-6 \). Die Kontrolle zeigt auch, dass wir richtig gerechnet haben, denn umgekehrt gilt \( (x^2-5x-6) \cdot (x-1)=x^3-6x^2-x+6 \).
Nun können wir z.B. mithilfe der Mitternachtsformel oder des Satzes von Vieta die Nullstellen von der quadratischen Funktion zu \( x_2= -1 \) und \( x_3 = 6 \) bestimmen und unsere Funktion \( f \) schreiben als \( f(x)=(x-1)\cdot(x+1)\cdot(x-6) \). Wir haben also das Problem eine Nullstelle eines Polynoms dritten Grades zu finden auf ein Polynom zweiten Grades reduziert.
Erste Nullstelle finden
Nun hatten wir in unserem Beispiel schon eine Nullstelle gegeben. Doch wie geht man vor, wenn man keinerlei Informationen besitzt? Dazu betrachten wir uns die faktorisierte Form eines normierten Polynoms an, also mit \( a=1 \). Dies hat dann die Form \( (x-x_1)\cdot (x-x_2) \cdot \dots \cdot (x-x_n) \). Multiplizieren wir dieses aus, so erhalten wir \( x^n + \dots + x_1 \cdot x_2 \cdot \dots \cdot x_n \). Das konstante Glied ist also Produkt aller Nullstellen. Umgekehrt heißt dies für die Nullstellensuche: Wir suchen Teiler des konstanten Glieds. Dies funktioniert in vielen Fällen auch, falls \( a \) bzw. \( a_n \) \( \ne 1 \) ist.
In unserem Beispiel \( x^3-6x^2-x+6 \) müssen wir also die Teiler von \( +6 \) betrachten. Diese sind (inkl. Vorzeichen!) \(-1, +1, -2, +2, -3, +3, -6, +6 \). In unserem Fall sind \( -1, +1 \) und \( +6 \) die Nullstellen und da wir ein Polynom dritten Grades vorliegen haben, haben wir auch schon alle Nullstellen gefunden, sodass man auch eine alternative Methode zur Polynomdivision hat. Allerdings funktioniert dies nicht immer, da manche Nullstellen z.B. Brüche oder irrational sein können und man diese eher schwer erraten kann (natürlich trotzdem "erlaubt").
Zum Abschluss hierzu noch ein wichtiger Satz, der aussagt, das z.B. in bestimmten Fällen sogar mindestens eine ganze Zahl, als Nullstelle auftreten muss.

Sei \( p \) ein normiertes (!) Polynom, das nur ganze Koeffizienten besitzt, d.h. \( a_k \in \mathbb{Z} \) für alle \( a_k \). Wenn \( \alpha \) eine rationale Nullstelle von \( p \) ist, dann ist \( \alpha \) eine ganze Zahl.
Insbesondere heißt dies (unter den Voraussetzungen des Satzes), dass wenn wir keine ganzen Nullstellen finden können (durch Suche der Teiler des konstanten Glieds), dass wir keinerlei rationale Nullstellen vorliegen haben, d.h. alle Nullstellen irrational oder komplex sind.
Betrachtet man nun unendliche Summen von Potenzfunktionen, so erhält man "Potenzreihen".

Sei \((a_k)_k\) eine Folge reeller Zahlen und \(x,a \in \mathbb{R}\). Dann heißt die Reihe
\(\sum_{k=0}^\infty {a_k (x-a)^n}\)
Potenzreihe mit Koeffizienten \(a_k\) und Entwicklungspunkt \(a\).
Polynome sind also ein Spezialfall von Potenzreihen, bei denen unendlich viele Koeffizienten (z.B. ab \( a_{n+1} \)) gleich \(0\) sind.
Potenzreihen stellen ein mächtiges Werkzeug in der Analysis dar. Im Folgenden geben wir zwei Beispiele für Potenzreihen. Ausführlich werden diese in der Analysisvorlesung zu Studienbeginn behandelt.
Die geometrische Reihe
\(\sum_{k=0}^\infty {x^k}\)
konvergiert für alle \(x \in (-1; 1)\). Hier stellt sie die Funktion \(f\) mit
\(f (x) = \frac{1}{1-x}\)
dar.

Zeigen Sie dies, indem Sie für spezielle x-Werte die Summe der ersten \(2, 3, 4, 5, \ldots\) Glieder berechnen.
Die Funktion \(f\) mit
\(f(x) = \sum_{k=0}^\infty {\frac{1}{k!} x^k}\)
ist auf ganz \(\mathbb{R}\) definiert. Mehr zu dieser speziellen Funktion lernen wir im nächsten Kapitel...

Berechnen Sie für spezielle x-Werte die Summe der ersten \(2, 3, 4, 5, \ldots\) Reihenglieder.

- Skizzieren Sie den Verlauf folgender Potenzfunktionen: \(x^3\), \(x^{\frac{1}{3}}\), \(x^{-3}\), \(x^{- \frac{1}{3}}\)
- Geben Sie für die Polynomfunktion mit \(f(x) = - \frac{1}{4} x^4 + \frac{3}{2} x^2 - 2x -2\) Art und Lage der Extrempunkte, die Wendepunkte und die Nullstellen an.

3.5. Exponentialfunktion und Logarithmus


In diesem Kapitel lernen wir eine besonders wichtige Funktion kennen - die Exponentialfunktion. Danach werden wir das Wachstum beliebiger Funktionen an Hand des Wachstums bereits bekannter Funktionen kategorisieren.
Einführendes Beispiel: Lineares und exponentielles Wachstum
Kapitalentwicklung bei einfacher Verzinsung
Bei einer einfachen Verzinsung werden in jedem Jahr nur die einfachen Zinsen in der Höhe von \(K_0 \cdot \frac{p}{100}\) zum Anfangskapital \(K_0\) hinzugerechenet. Die Zinsen der weiteren Jahre werden immer nur vom Anfangskapital \(K_0\) berechnet. Es wird also davon ausgegangen, dass die jährlichen Zinsen an den Anleger ausbezahlt werden. Es ergibt sich für das Kapital nach \(n\) Jahren
\(K(n) = K_0 + K_0 \cdot \frac{p}{100} \cdot n\)
Kapitalentwicklung mit Zinseszins
Bei einer Verzinsung mit Zinseszinsen werden jedes Jahr die Zinsen der vorangegangenen Jahre wiederum verzinst, d.h. das Anfangskapital \(K_0\) wird im jedem Jahr mit \((1 + \frac{p}{100})\) multipliziert. Es ergibt sich für das Kapital nach \(n\) Jahren
\(K(n) = K_0 \cdot (1 + \frac{p}{100})^n\)

Erläutern Sie das Zustandekommen dieser Formel.
Näherungsweise kann man aber auch mit einem Exponenten \(x \in \mathbb{R}\) arbeiten, um das Kapital zu beliebigen Zeitpunkten (z.B. \(x = 1, 75\) Jahre) zu berechnen. Der Graph für das Kapital nach einer beliebigen Zeitspanne \(x\) besteht in diesem Fall aus einer stetigen Kurve. (Diese kontinuierliche Entwicklung kann in den Applets über das Kontrollkästchen ein- bzw. ausgeschaltet werden.)
Das Anwachsen eines Kapitals nach der Funktionsgleichung \(K(x) = K_0 \cdot (1 +\frac{p}{100})^x\) nennt man exponentielles Wachstum. Dieses Wachstum wird durch die Funktionsgleichung eines neuen Funktionstyp beschrieben. Bei dieser Art von Funktion steht die unabhängige Variable \(x\) im Exponenten und wird deshalb Exponentialfunktion genannt.
Die allgemeine Exponentialfunktion

Die Funktion
\(f: \mathbb{R} \rightarrow \mathbb{R}, \, f(x) = a^x = \exp (x \cdot \log(a))\,\) für \(a \in \mathbb{R}^+\)
heißt Exponentialfunktion zur Basis \(a\).
\(a>0\) wird hier echt positiv gewählt, da für \(a<0\) bspw. Ausdrücke der Form \(a^{\frac{1}{2}}=\sqrt{a}\) in \(\mathbb{R}\) nicht lösbar sind.
Für \(a=0\) hingegen sind bspw. Ausdrücke der Form \(a^{-1}=\frac{1}{a}\) nicht definiert.

Für alle \(x,y \in \mathbb{R}\) gilt:
\(a^{(x+y)} = a^x \cdot a^y\)

- Die Exponentialfunktion ist für alle \(x \in \mathbb{R}\) definiert.
- Sie nimmt nur positive Funktionswerte an.
- Die Graphen aller Exponentialfunktionen der Form \(f(x) = a^x\) gehen durch den Punkt \((0|1)\).
- Für \(0 < a < 1\) ist \(f(x)\) monoton fallend, für \(a = 1\) konstant und für \(a > 1\) monoton steigend.
- Die Graphen von \(f(x) = a^x\) und \(g(x) = a^{-x}=\frac{1}{a^x}\) liegen symmetrisch bezüglich der y-Achse. Für beide Graphen ist die x-Achse horizontale Asymptote.
- Für \(0 < a < 1\) ist \(f(x) = a^x\) monoton fallend, \(f\) divergiert für \(x \rightarrow -\infty\) und konvergiert gegen \(0\) für \(x \rightarrow \infty\)
- Für \(a=1\) ist \(f\) konstant
- Für \(a > 1\) ist \(f(x) = a^x\) monoton steigend, \(f\) divergiert für \(x \rightarrow \infty\) und konvergiert gegen \(0\) für \(x \rightarrow -\infty\)
Es gilt: \(a^0=1\) für alle \(a\)
Es gilt: \(1^x=1\) für alle \(x\)
\(f(-x) = a^{-x} = g(x)\)
\(f(x) = a^{x} = a^{-(-x)} = g(-x) \)

- (Diskussion von \(x \mapsto a^x\)) Stellen Sie zunächst für \(m\) und \(b\) den Wert \(1\), für \(c\) und \(d\) den Wert \(0\) ein und ändern Sie mit Hilfe des Schiebereglers den Wert der Basis \(a\) und beschreiben Sie den Verlauf des Schaubildes für verschiedene Werte von \(a\). Verifizieren Sie die oben genannten Eigenschaften der Funktion \(x \rightarrow a^x\).
- (Diskussion von \(x \mapsto m \cdot a^x\)) Lassen Sie wiederum \(a\) fest (nicht \(0\)) und veränderen Sie nur \(m\). Beschreiben Sie die Auswirkungen auf das Schaubild und finden Sie eine bestimmte Eigenschaft für bestimmte Wertepaare von \(m\) heraus.
- (Diskussion von \(x \mapsto a^{b \cdot x}\)) Lassen Sie nun \(a\) fest (nicht \(0\)) und verändern Sie nur \(b\). Beschreiben Sie die Auswirkungen auf das Schaubild und finden Sie eine bestimmte Eigenschaft für bestimmte Wertepaare von \(b\) heraus.
- (Diskussion von \(x \mapsto a^x+ c\)) Stellen Sie für \(m\) und \(b\) wieder den Wert \(1\) und für \(d\) den Wert \(0\) ein und ändern Sie mit Hilfe des Schiebereglers den Wert von \(c\). Beschreiben Sie die Auswirkungen auf das Schaubild.
- (Diskussion von \(x \mapsto a^{x+d}\)) Stellen Sie für \(m\) und \(b\) wieder den Wert \(1\) und für \(c\) den Wert \(0\) ein und ändern Sie mit Hilfe des Schiebereglers den Wert von \(d\). Beschreiben Sie die Auswirkungen auf das Schaubild.
Der Logarithmus - die Umkehrfunktion der Exponentialfunktion
Die Umkehrfunktion der Exponentialfunktion zur Basis \(a>0\) ist der Logarithmus \(\log_a(x) : \mathbb{R}^+ \rightarrow \mathbb{R}\). Er ist stetig und streng monoton wachsend.
Die Logarithmus-Funktion ergibt sich als Umkehrfunktion durch Umformen der Exponentialfunktion:
\(y=f(x)=a^x\)
Dann ist:
\(x=f^{-1}(y)=log_a(y)\)
Um die Funktion im gewohnten Koordinatensystem darzustellen, wird sie allerdings ebenfalls in der Form \(x \rightarrow f^{-1}(x)\) verwendet.

- Ändern Sie mit Hilfe des Schiebereglers den Wert von \(a\) und beschreiben Sie den Verlauf des Schaubildes für verschiedene Werte von \(a\). Was haben alle Funktionen gemeinsam? Welche Unterschiede für welche \(a\) gibt es?
- Was fällt Ihnen im Vergleich von Exponentialfunktion und Logarithmusfunktion auf? Beschreiben Sie die Lage beider Schaubilder zueinander.

Für alle \(x, y \in \mathbb{R}^+\) gilt:
\(\log_a(x \cdot y) = \log_a(x) + \log_a(y)\)


3.6. Trigonometrische Funktionen


Allgemeine Grundlagen zu trigonometrischen Funktionen
Dieses Kapitel führt kurz die grundlegenden trigonometrischen Funktionen sowie deren Eigenschaften ein. Der Sinus, Cosinus und Tangens sind aus der Schule v.a. zur Berechnung von Längenverhältnissen bekannt, können aber auch als Funktionen aufgefasst werden. In untenstehendem Applet kann der Zusammenhang für Sinus/Kosinus zwischen der Anwendung in der Geometrie und als Funktion untersucht werden.
Umrechnung:
\(90°=\frac{\pi}{2}\)
\(180°=\pi \)
\(360°=2\pi\)

Sinusfunktion
Definition Sinus:
Die Funktion \( sin : \mathbb{R} \rightarrow [-1,1], x \mapsto sin(x) \) heißt Sinusfunktion. Ihr Definitionsbereich ist \( \mathbb{R} \) und ihr Wertebereich \( [-1,1] \).Eine Möglichkeit sie zu definieren, ist als Potenzreihe:
\[ sin(x):= \sum_{k=0}^\infty (-1)^k \frac{x^{2k+1}}{k!} \]
Sie ist eine periodische Funktion mit Periode \( 2\pi \), d.h. es gilt \( sin(x)=sin(x+2\pi) \) für alle \( x \in \mathbb{R} \). Graphisch heißt das, dass sich der Graph nach \( 2\pi \) stets wiederholt. Dies kann man auch an der Betrachtung am Einheitskreis erkennen, da sich nach exakt einer Umdrehung (also nach \(2\pi\)) das Schaubild nicht geändert hat.
Wie man in obigem Applet erkennen kann, besitzt sie bei \( 0 \) und \( \pi \) jeweils eine Nullstelle. Aufgrund der Periodizität hat die Sinusfunktion unendlich viele Nullstellen, die jeweils bei ganzzahligen Vielfachen von \( \pi \) liegen. D.h. es gilt \( sin(x)=0 \Leftrightarrow x=k \cdot \pi \) mit \( k \in \mathbb{Z}\).
Es gilt \( -sin(x)=sin(-x) \), d.h. der Sinus ist Punktsymmetrisch zum Ursprung. Erläuterbar ist das z.B. anhand der Potenzreihe, da hier nur ungerade Exponenten auftauchen. Setzt man nun \( -x \) in \( sin \) bzw. die Potenzreihe ein, so kann man ein \( -1 \) ausklammern und erhält \( - sin(x)=sin(-x) \).
Aufgabe:
Im Folgenden wollen wir die Abhängigkeit der allgemeinen Sinusfunktion \( a \cdot sin(bx+c) + d \) von ihren Paramtern \( a,b,c,d \in \mathbb{R} \) näher untersuchen. Dazu dient nachfolgendes Applet zum Ausprobieren.
Erläutern Sie die Auswirkungen jedes Parameters unter Benutzung der Begriffe Stauchung, Streckung und Verschiebung. Durch welchen Parameter kann man die Periodizität darstellen?
Hinweis: Der besseren Übersicht halber wurde der Paramter \( c \) durch \( p \cdot \pi \) ersetzt.

Kosinusfunktion
Definition Kosinus:
Die Funktion \( cos : \mathbb{R} \rightarrow [-1,1], x \mapsto cos(x) \) heißt Kosinusfunktion. Ihr Definitionsbereich ist \( \mathbb{R} \) und ihr Wertebereich \( [-1,1] \).Eine Möglichkeit sie zu definieren, ist als Potenzreihe:
\[ cos(x):= \sum_{k=0}^\infty (-1)^k \frac{x^{2k}}{k!} \]
Aufgabe:
Im Folgenden wollen wir die Abhängigkeit der allgemeinen Kosinusfunktion \( a \cdot cos(bx+c) + d \) von ihren Paramtern \( a,b,c,d \in \mathbb{R} \) näher untersuchen sowie den Zusammenhang zur Sinusfunktion. Dazu dient nachfolgendes Applet zum Ausprobieren.
Erläutern Sie die Auswirkungen jedes Parameters unter Benutzung der Begriffe Stauchung, Streckung und Verschiebung. Durch welchen Parameter kann man die Periodizität darstellen?
Welche(n) Paramter muss man um wie viel verschieben, sodass der Kosinus mit der Funktion \( x \mapsto sin(x) \) übereinstimmt? Ist die Lösung eindeutig oder gibt es mehrere Möglichkeiten?
Hinweis: Der besseren Übersicht halber wurde der Paramter \( c \) durch \( p \cdot \pi \) ersetzt.

Tangensfunktion
Wir wollen nun die Eigenschaften und das Aussehen der Tangensfunktion mithilfe unseres bisherigen Wissens herleiten. Dazu beachten wir, dass
\[ tan (x) = \frac{sin(x)}{cos(x)} \]
gilt.
Der Sinus hat für ganzzahlige Vielfache von \( \pi \) Nullstellen und der Kosinus ist für diese Werte ungleich \( 0 \). Damit hat der Tangens genau dann Nullstelen, wenn \( x \) ein ganzzahliges Vielfaches von \( \pi \) ist - analog zum Sinus.
Wir haben aber auch gesehen, dass der Kosinus für \( x = \frac{2k+1}{2} \cdot \pi \) mit \( k \in \mathbb{Z} \) Nullstellen besitzt. Da man nicht durch \( 0 \) teilen kann, ist der Tangens hier nicht definiert. Die Frage ist nun, wie sich der Graph in der Umgebung einer solchen Definitionslücke verhält. Wir wollen das exemplarisch für \( \frac{\pi}{2} \) erörtern:
Zunächst betrachten wir das Verhalten des Graphen links von \( x = \frac{\pi}{2} \), indem wir Werte betrachten, die minimal kleiner sind als \( x \). Wir wählen also ein "sehr kleines" \( \epsilon > 0 \) und betrachten \( x- \epsilon \). Aus den Graphen von Sinus und Cosinus kann man dann ablesen, dass \( sin(x-\epsilon) \) nahe \( +1 \) ist und \( cos(x-\epsilon) \) nahe \( 0 \), aber positiv. Betrachten wir nun \( tan(x-\epsilon) \) so muss dieser Wert dann gegen \( + \infty \) streben. Analog kann man eine Betrachtung rechts von \( x = \frac{\pi}{2} \) durchführen, indem man \(x + \epsilon \) einsetzt. Wiederum ist \( sin(x+\epsilon) \) nahe \( +1 \) und \( cos(x+\epsilon) \) nahe \( 0\), aber diesmal negativ. Damit strebt der Tangens von \( x+\epsilon \) für kleine Epsilon diesmal gegen \( - \infty \).
Diese Überlegung kan man nun für jede Definitionslücke durchführen. Man kann sich aber einiges an Arbeit ersparen, indem man den Tangens hinsichtlich Symmetrie untersucht. Dazu setzten wir \( -x \) ein:
\( tan (-x)= \frac{sin(-x)}{cos(-x)}=\frac{-sin(x)}{cos(x)}=- \frac{sin(x)}{cos(x)}=- tan(x) \)
Damit ist der Tangens also punktsymmetrisch und wir können z.B. aussagen, dass deshalb der Graph rechts von \( x = - \frac{\pi}{2} \) gegen \( - \infty \) strebt. Unten ist zur Veranschaulichung der Graph der Tangensfunktion dargestellt. In diesem kann man gut erkennen, dass der Tangens auch periodisch ist mit Periode \( \pi \)

Arkusfunktionen
Zuletzt wollen wir die Umkehrfunktionen von Sinus, Kosinus und Tangens betrachten. Diese Tragen jeweils das Präfix arc-, das ein Kürzel für Arkus darstellt. Sie heißen also Arcsin, Arccos und Arctan. Auf einigen Taschenrechnern findet man alternativ auch z.B. das Symbol \( sin^{-1} \); dies ist mathematisch aber eigentlich falsch, da es sich dabei um den Kehrwert \( \frac{1}{sin} \) handelt.
In geometrischer Hinsicht setzt man bei trigonometrischen Funktionen einen Wert eines Winkels ein und erhält eine reelle Zahl und setzt umgekehrt bei Arkusfunktionen eine reelle Zahl ein und erhält einen Wert eines Winkels, wobei die reelle Zahl aus dem Wertebereich der zugehörigen trigonomerischen Funktion stammt.
Dazu ein Beipiel: Gesucht ist der Winkel \( \alpha \) für den \( sin(\alpha) = 0,5 \) gilt, also der Wert \( arcsin(0,5)\). Ablesen aus dem Graphen des Sinus liefert (nahe der \(y\)-Achse) den Wert \( 30° \) bzw. umgerechnet \( \frac16 \pi \). Allerdings kann man auch \( sin(\frac56 \pi)=0,5 \) ablesen. Und aufgrund der Periodizität sind auch \( \frac16 \pi + 2k\pi \) sowie \( \frac56 \pi +2k\pi \) mit \(k \in \mathbb{Z} \) Lösungen. Damit wäre aber \( arcsin(0,5) \) nicht eindeutig definiert, im Widerspruch dazu, dass \( arcsin \) eine Funktion sein soll. Aus diesem Grund schränkt man zur Definition das Intervall des Bildbreichs der Arkusfunktionen ein.
Definition Arkusfunktionen:
Die Funktion \( arcsin : [-1,1] \rightarrow [-\frac{\pi}{2},\frac{\pi}{2}], x \mapsto arcsin(x) \) heißt Arkussinusfunktion.Die Funktion \( arccos : [-1,1] \rightarrow [0, \pi ], x \mapsto arccos(x) \) heißt Arkuscosinusfunktion.
Die Funktion \( arctan : \mathbb{R} \rightarrow (-\frac{\pi}{2},\frac{\pi}{2}), x \mapsto arctan(x) \) heißt Arkustangensfunktion.
Beachte, dass beim Arkussinus und Arkuskosinus die Intervallgrenzen des Bildbereichs auch erreicht werden können (z.B. ist \( arccos(1)=0 \)), wohingegen die Grenzen \(-\frac{\pi}{2} \) und \( \frac{\pi}{2} \) beim Arkustangens nie erreicht werden können, da der Tangens hier Definitionslücken besitzt.
Außerdem besitzt die Tangensgleichung \( tan(x)=a \) Lösungen für alle reellen Werte von \( a \), wohingegen die Gleichungen \( sin(x)=a \) und \( cos(x)=a \) keine Lösungen besitzen, wenn \( a \) nicht im Intervall \( [-1,1] \) liegt.
Zur Veranschaulichung sind hier auch die Graphen der drei Funktionen dargestellt. Auffällig ist, dass die Funktionen ihre Symmterie behalten haben. So ist der Arkuskosinus achsensymmetrisch zur \(y\)-Achse und der Arkussinus sowie Arkustangens punktsymmetrisch zum Ursprung.

3.7. Aufgaben


Aufgabe 1: Parabeln I
Die Graphen der Funktionen \(f\), \(g\) mit \(f(x) = ax^2+ bx + c\) und \(g(x) = d(x-e)^2+ h\) sollen dieselbe Parabel darstellen. Welche Beziehung besteht zwischen den Variablen \(a\), \(b\), \(c\), \(d\), \(e\) und \(h\)?
Aufgabe 2: Parabeln II
Wir betrachten die Parabeln \(P_b\) mit der Gleichung \(f_b(x) = 2x^2+ bx + 1\), \(b \in \mathbb{R}\).
- Bestimmen Sie den Scheitelpunkt \(S_b\) der Parabeln \(P_b\) (also in Abhängigkeit von \(b\)).
- Zeichnen Sie – etwa mit Hilfe des Programms GeoGebra (kostenlos downloadbar unter http://www.geogebra.org) – die Ortslinie \(OS_b\), auf der sich der Scheitelpunkt von \(P_b\) bewegt, wenn \(b\) variiert wird. In die Lösung der Aufgabe soll ein Screenshot dieser Aufgabe eingebunden werden.
- Bestimmen Sie die Gleichung für die Ortslinie \(OS\).
Aufgabe 3: Exponentialfunktion
- Vergleichen Sie die beiden Funktionen mit \(y = a \cdot 2^x\) und \(y = 2^{(x+d)}\) für verschiedene Werte \(a,d \in \mathbb{R}\). Für welche \(a\) bzw. \(d\)-Werte stimmen die Graphen der beiden Funktionen überein?
- Die allgemeine Exponentialfunktion lässt sich mit der Gleichung \(f(x) = a \cdot b^{cx+d}\) mit \(a,c,d \in \mathbb{R}; b \in \mathbb{R}^+\) beschreiben. Diese Gleichung ist äquivalent zu einer Gleichung mit nur drei Parametern \(A,B,C\), wobei \(A,B,C \in \mathbb{R}\) bzw. \(\mathbb{R}^+\). Geben Sie den Zusammenhang zwischen \(A,B\) und \(C\) sowie \(a,b,c\) und \(d\) an!
Aufgabe 5: Quadratische Ergänzung
Aufgabe 6: Nullstellen und Extrema
- \(f(x) = -\frac{1}{2} x^2 + \frac{1}{2} x + 3\)
- \(g(x) = 2 \cdot sin(x+3)+4\)
- \(h(x) = e^x\)
- \(h(x) = e^x-1\)

4. Funktionen II


Das Kapitel Funktionen II schließt sich an das Kapitel Funktionen I. Es umfasst:

- Grenzwerte von Funktionen
- Rechnen mit Grenzwerten von Funktionen
- Stetigkeit
- Kurven und Abbildungen
- Aufgaben

4.1. Grenzwert einer Funktion

In diesem Abschnitt wird das Konzept des Grenzwerts einer Funktion an einer bestimmten Stelle entwickelt.
Die folgenden Voraussetzungen gelten für den gesamten Abschnitt: \[f \colon S \to \mathbb{R}\]
Hierbei ist \(S\) eine Teilmenge der reellen Zahlen und \(x_0\) ist eine Häufungspunkt der Menge \(S\). Das heißt, es gibt eine Folge \( \left( x_k \right)_{k \in \mathbb{N}} \), so dass gilt:
-
\( x_k \in S \) für alle \(k \in \mathbb{N} \)
-
\( x_k \to x_0 \) für \(k \to \infty \)
Bemerkung: Falls \(x_0\) ein Häufungspunkt der Menge \(S\) ist, so muss \(x_0\) nicht notwendiger Weise zur Menge \(S\) gehören. Betrachten wir das folgende Beispiel:
Beispiel 1.
\[ S = \left] 0, 1 \right], x_0 = 0 \]
Es sei \( x_k = \frac{1}{k} \). Dann gilt \( x_k \in S\) für alle \( k \in \mathbb{N} \) und \( x_k \to 0 \) für \( k \to \infty \), obwohl die Zahl \(0\) nicht zur Menge \( \left] 0, 1 \right] \) gehört.

Grenzwert einer Fuktion
Wir wollen zunächst ein Beispiel betrachten:
Es sei \[f(x)=\frac{x^2-9}{x^2-5x+6}.\]
Wegen \( x^2-5x+6 = (x-3) \cdot (x-2) \) hat der Nenner die Nullstellen \( x = 2 \) sowie \( x = 3 \) und damit dort Definitionslücken, da der Nenner nicht \( 0 \) werden darf. Allerdings ist nach der dritten binomischen Formel der Zähler \( x^2-9 = (x-3) \cdot (x+3) \). Wir könnten also den Faktor \( (x-3) \) herauskürzen und hätten damit eine Definitionslücke "eliminiert".
Die Funktion nähert sich in einer Umgebung um die Definitionslücke einem Wert, den man Grenzwert der Funktion nennt. Diesen wollen wir nun mathematisch definieren.
Definition 1 (Grenzwert einer Funktion)
Es sei \( f \colon S \to \mathbb{R} \) eine Funktion und \( x_0 \) ein Häufungspukt der Menge \(S\).
Wir sagen, dass die Funktion \( f(x) \) den Grenzwert \( y_0 \) an der Stelle \( x_0 \) hat, falls \( f(x_k) \to y_0 \) für jede mögliche Folge \( x_k \) mit \( x_k \to x_0 \) gilt. Abkürzend schreiben wir \[ \lim\limits_{x \to x_0} f(x) = y_0 .\]
Bemerkung: Diese Definition heißt auch Folgendefinition des Grenzwertes einer Funktion und verwendet des Konzept des Grenzwertes von Folgen. Wir werden in diesem Kapitel später noch eine andere (dazu äquivalente) Definition des Grenzwertes einer Funktion kennenlernen.
Wir wollen unser Eingangsbeispiel aufgreifen:
\[f(x)=\frac{x^2-9}{x^2-5x+6}.\] Wir untersuchen die Funktion \(f\) in der Umgebung der Stelle \(3\): \[\lim_{x\to3} f(x)=\lim_{x\to3}\frac{x^2-9}{x^2-5x+6}=\lim_{x\to3}\frac{(x-3)(x+3)}{(x-3)(x-2)}=\lim_{x\to3}\frac{x+3}{x-2}=6\]
Beispiel 2.
Die Funktion \( g(x) \colon \mathbb{R} \to \mathbb{R} \), definiert durch \( g(x) = \sin (x) \) hat den Grenzwert \( \lim\limits_{x \to 0} g(x) = 0 \). Denn jede Folge \( (\sin (x_k)) \) konvergiert gegen \( 0 \) , wenn \( (x_k) \) gegen \( 0 \) konvergiert.
Man betrachtet hier die Sinusfunktion in der nahen Umgebung vom Nullpunkt. Je näher die x-Werte an der Null sind, desto kleiner wird \( \sin (x) \), egal ob man negative oder positive x-Werte einsetzt, da der Sinus achsensymmetrisch an der y-Achse ist. Somit macht es keinen Unterschied, ob man positive oder negative x-Werte betrachtet. Da \( (x_k)\) gegen \(x_0 = 0\) konvergiert und der Sinus immer kleiner wird für die Folge \( (x_k) \) und sich der Null annähert, konvergiert \( (\sin (x_k)) \) gegen \( \sin (x_0) = \sin (0) = 0 \).
Beispiel 4.
Betrachte die Funktion \( h(x) \colon \mathbb{R} \backslash \{ 0 \} \to \mathbb{R} \), definiert durch \( h(x) = \sin \left( \frac{1}{x} \right) \).
Der Punkt \( x_0 = 0 \) ist ein Häufungspunkt der Definitionsmenge der Funktion \( h \), obwohl \(x_0\) nicht zur Definitionsmenge gehört.
Existiert der Grenzwert der Funktion \( h \) an der Stelle \( x_0 = 0 \)? Um diese Frage zu beantworten, betrachten wir zunächst die Folge: \[ \left( a_k \right) \text{ mit } a_k = \frac{1}{2 \pi k}, k \in \mathbb{N} \].
Wir berechnen nun die von dieser Folge induzierte Grenzwerte der Funktion \( h \).
\[ \lim\limits_{a_k \to 0} h(a_k) = \lim\limits_{ a_k \to 0 } \sin \frac{1}{a_k} = \lim\limits_{ \frac{1}{2 \pi k} \to 0 } \sin 2 \pi k = \lim\limits_{ \frac{1}{2 \pi k} \to 0 } 0 = 0 \]
Wir sehen, dass der Grenzwert für diese spezielle Folge existert. Dies können wir jedoch nicht verallgemeinern. Betrachten wir dazu die Folge
\[ \left( b_k \right) \text{ mit } b_k = \frac{2}{(2 k + 1) \pi}, k \in \mathbb{N} \]
Es gilt
\[ \lim\limits_{b_k \to 0} h(b_k) = \lim\limits_{ b_k \to 0 } \sin \frac{1}{b_k} = \lim\limits_{ \frac{2}{(2 k + 1) \pi} \to 0 } \sin \frac{(2 k + 1)}{2}\pi = \lim\limits_{ \frac{2}{(2 k + 1) \pi} \to 0 } \sin \frac{(2 k + 1)}{2}\pi \]
Die Werte des Terms \( \sin \frac{(2 k + 1)}{2}\pi \) alternieren zwischen \( +1 \) und \( -1 \) in Abhängigkeit des Wertes von \( k \). Daher existiert der Grenzwert \[ \lim\limits_{ \frac{2}{(2 k + 1) \pi} \to 0 } \sin \frac{(2 k + 1)}{2}\pi \] nicht. Daraus können wir nun allgemein folgern, dass der Grenzwert \( \lim\limits_{k\to\infty} h(b_k) \) ebenfalls nicht existiert. Denn würde dieser existieren, so müsste er für jede Folge \( \left( c_k \right), k \in \mathbb{N} \) existieren, was wir widerlegt haben.
Offensichtlich ist die Folgendefinition des Grenzwerts gut geeignet, um zu zeigen, dass der Grenzwert einer Funktion nicht existiert. Man benötigt lediglich zwei Folgen \( \left( a_k \right)_{k \in \mathbb{N}} \) und \( \left( b_k \right)_{k \in \mathbb{N}} \), die beide gegen den Wert \( x_0 \) konvergieren, wohingegen die korrespondierenden Folgen \( \left( f(a_k) \right)_{k \in \mathbb{N}} \) und \( \left( f(b_k) \right)_{k \in \mathbb{N}} \) gegen verschiedene Werte konvergieren.

Satz 1.
Falls eine Funktion an einer Stelle einen Grenzwert hat, so ist dieser eindeutig bestimmt.

Einseitige Grenzwerte
In Beispiel 4 hatten wir eine Funktion kennengelernt, die keinen Grenzwert an der Stelle \(0\) hatte. Dies lag daran, dass sich bei Annäherung von links an die Stelle \(0\) ein anderer Grenzwert ergeben hat als von rechts.
Wir können das zu untersuchende Gebiet auf eine "einseitige Menge" wie beispielsweise \( S = \left]0, 1 \right[ \) für \( x_0 = 0 \) oder \( S = \left]0.5, 2 \right[ \) für \( x_0 = 2 \) einschränken. Die dadurch erhaltenen Grenzwerte heißen einseitige Grenzwerte.
Definition 2 (Grenzwert einer Funktion)
Es sei \(S\) eine Teilmenge von \(\mathbb{R}\) und \(f\) eine auf \(S\setminus\{x_0\}\) definierte Funktion. Dann hat \(f\) einen linksseitigen Grenzwert \(y_{0}\) an der Stelle \(x_{0}\), falls \(f(x_{k})\to y_{0}\) für \(k\to \infty\) für jede Folge \((x_{k})\) gilt, die in der Menge \( S \cap \left] - \infty , x_0 \right[ = \{ x \in S : x < x_0 \} \) liegt und für die \(x_{k}\to x_{0}\) für \(k\to \infty\) gilt. Wir schreiben dafür \[\lim_{x \to x_{0}-}f(x)=y_{0},\]
Analog hat \(f\) einen rechtsseitigen Grenzwert \(y_{0}\) an der Stelle \(x_{0}\), falls \(f(x_{k})\to y_{0}\) für \(k\to \infty\) für jede Folge \((x_{k})\) gilt, die in der Menge \( S \cap \left] x_0, \infty \right[ = \{ x \in S : x > x_0 \} \) liegt und für die \(x_{k}\to x_{0}\) für \(k\to \infty\) gilt. Wir schreiben dafür \[\lim_{x \to x_{0}+}f(x)=y_{0},\]
Beispiel 5.
Berechne \[\lim_{x\to 5}\frac{x^2-6x+5}{x-5}\]
Es gilt \[\lim_{x\to 5}\frac{x^2-6x+5}{x-5}=\lim_{x\to 5}\frac{(x-5)(x-1)}{x-5}=\lim_{x\to5}(x-1)=4\]
Beispiel 6.
Berechne \[\lim_{x\to \infty}\frac{x-5}{x^2-6x+5}\]
Es gilt\[\lim_{x\to \infty}\frac{x-5}{x^2-6x+5}=\lim_{x\to\infty}\frac{x^2(\frac1x-\frac{5}{x^2})}{x^2(1-\frac{6}{x}+\frac{5}{x^2})}=\lim_{x\to\infty}\frac{\frac1x-\frac{5}{x^2}}{1-\frac{6}{x}+\frac{5}{x^2}}=0,\] da der Zähler gegen \(0\) und der Nenner gegen \(1\) geht.
Beispiel 7.
Es sei \[f(x)=\begin{cases}x^2-1,& {\rm~für~} x\leq2\\x+2, & {\rm~für~} x>2\end{cases}\] Berechne \(\lim_{x\to2}f(x)\).
Hier müssen wir einseitige Grenzwerte verwenden. Nähern wir uns der Stelle \(x_0=2\) von links, so gilt: \[\lim_{x\to2-}f(x)=\lim_{x\to2-}x^2-1=3.\] Nähern wir uns der Stelle \(x_0=2\) von rechts, so gilt: \[\lim_{x\to2+}f(x)=\lim_{x\to2+}x+2=4.\] In diesem Fall sind der linksseitige und rechtsseitige Grenzwert verschieden. Daher hat die Funktion eine Sprungstelle in der Umgebung von \(2\).
Beispiel 8.
Es sei \[f(x)=\begin{cases}\sin x,& {\rm~für~} x\leq\pi\\1+\cos x, & {\rm~für~} x>\pi\end{cases}\] Berechne \(\lim_{x\to\pi}f(x)\).
Hier können wir ebenfalls einseitige Grenzwerte verwenden. Nähern wir uns der Stelle \(x_0=\pi\) von links, so gilt: \[\lim_{x\to\pi-}f(x)=\lim_{x\to\pi-}\sin x=0.\] Nähern wir uns der Stelle \(x_0=\pi\) von rechts, so gilt: \[\lim_{x\to\pi+}f(x)=\lim_{x\to\pi+}1+\cos x=0.\]
In diesem Fall sind die einseitigen Grenzwerte gleich.

Übung 1.
Berechne für die nebenstehend dargestellte Funktion \(f\) die nachfolgenden Grenzwerte
a) \(\lim_{x \to -2-} f(x)\)
b) \(\lim_{x \to 1-} f(x)\)
c) \(\lim_{x \to 2-} f(x)\)
d) \(\lim_{x \to 2+} f(x)\)
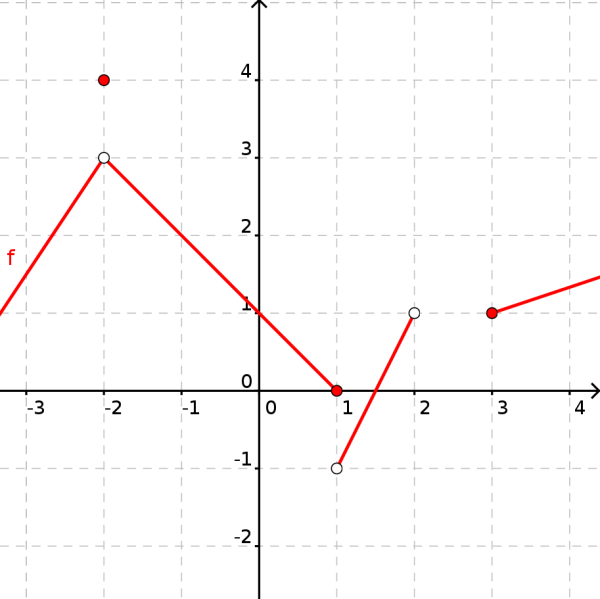




4.2. Rechnen mit Grenzwerten von Funktionen

In diesem Abschnitt werden die Rechenregeln mit Grenzwerten erläutert und angewendet.
Bekanntlich kann man in den reellen Zahlen \( \mathbb{R} \) die nachfolgenden vier elementaren Rechenoperationen ausführen:
-
Addition: \(a+b\)
-
Subtraktion: \(a-b\)
-
Multiplikation: \(a\cdot b\)
-
Division: \(a\colon b\)
Diese Rechenoperationen gelten jedoch nicht nur für Zahlenmengen wie \(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\) oder \(\mathbb{R}\), sondern auch für Funktionen. Beispielsweise gilt:
-
Das Ergebnis der Addition der beiden Funktionen \( a(x) = 2x \) und \( b(x) = x^2 \) ist die Funktion \( (a+b)(x) = 2x + x^2 \)
-
Das Ergebnis der Subtraktion der Funktion \( b(x) = 4x \) von \( a(x) = 7x+2 \) ist die Funktion \( (a-b)(x) = (7x+2) - 4x = 3x+2 \)
-
Die Multipikation der Funktionen \( a(x) = x+1 \) und \( b(x) = x-1 \) liefert \( (a\cdot b)(x) = (x+1) \cdot (x-1) = x^2 -1\)
-
Die Funktion \( a(x) = x+3 \), dividiert durch die Funktion \( b(x) = x^3 \) liefert \( \left( \frac{a}{b} \right) (x) = \frac{x+3}{x^3} \)
Diese arithmetischen Rechenoperationen können können nicht nur auf Funktionen, sondern auch (mit gewissen Einschränkungen) auf Grenzwerte von Funktionen übertragen werden. Davon handelt das nächste Theorem:

Satz 1.
Es sei \( c \in \mathbb{R} \), \( \lim \limits_{ x \to x_0 } f(x) = a \) und \( \lim \limits_{ x \to x_0 } g(x) = b \). Dann gelten die folgenden Regeln:
-
\( \lim \limits_{x \to x_0 } c f(x) = ca \)
-
\( \lim \limits_{x \to x_0 } (f+g)(x) = a+b \)
-
\( \lim \limits_{x \to x_0 } (f \cdot g)(x) = a \cdot b \)
-
\( \lim \limits_{x \to x_0 } \left( \frac{f}{g}\right) (x) = \left( \frac{a}{b} \right) \) (sofern \( b \neq 0 \))
Bemerkung: Man beachte, dass eine Subtraktionsregel für Grenzwerte in Theorem 1 nicht explizit erwähnt wird. Diese Regel folgt nämlich direkt aus der ersten und dritten Regel:
\[ \lim \limits_{x \to x_0 } (f-g)(x) = \lim \limits_{x \to x_0} (f(x) + (-1) \cdot g(x)) = \lim \limits_{x \to x_0} f(x) + \lim \limits_{x \to x_0} ( -1 \cdot g(x) ) = \]
\[ = \lim \limits_{x \to x_0} f(x) + (-1) \cdot \lim \limits_{x \to x_0} g(x) = \lim \limits_{x \to x_0} f(x) - \lim \limits_{x \to x_0} g(x) \]
Beispiel 1.
Berechne \[\lim \limits_{x\to2}(x^2-x).\] Hier ist \(f(x)=x^2\) und \(g(x)=x\). Aus \[\lim\limits_{x\to2}f(x)=\lim\limits_{x\to2}x^2=(\lim\limits_{x\to2}x)\cdot(\lim\limits_{x\to2}x)=2\cdot2=4\] und \[\lim\limits_{x\to2}g(x)=2\] erhält man \[\lim \limits_{x\to2}(x^2-x)=\lim \limits_{x\to2}f(x)-\lim\limits_{x\to2}g(x)=4-2=2.\]
Beispiel 2.
Berechne \[\lim\limits_{x\to\frac{\pi}{4}}\frac{\sin{x}}{\cos{x}}.\] Hier ist \(f(x)=\sin x\) und \(g(x)=\cos x\) und \[\lim\limits_{x\to\frac{\pi}{4}}\sin x=\frac{\sqrt{2}}{2},\quad\lim\limits_{x\to\frac{\pi}{4}}\cos x =\frac{\sqrt{2}}{2}.\] Damit erhält man \[\lim\limits_{x\to\frac{\pi}{4}}\frac{f(x)}{g(x)}=\frac{\lim\limits_{x\to\frac{\pi}4}f(x)}{\lim\limits_{x\to\frac{\pi}{4}}g(x)}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}=1.\]
Beispiel 3.
Berechne \[\lim\limits_{x\to\pi}\frac{x\sin x}{\cos x}.\] Wir geben nun eine verkürzte Lösung an. Es gilt: \[\lim\limits_{x\to\pi}\frac{x\sin x}{\cos x}=\frac{\lim\limits_{x\to\pi}(x\sin x}{\lim\limits_{x\to\pi}\cos x}=\frac{(\lim\limits_{x\to\pi}x)\cdot(\lim\limits_{x\to\pi}\sin x)}{\lim\limits_{x\to\pi}\cos x}=\frac{\pi\cdot0}{-1}=0.\]

Grenzwert einer Komposition von Funktionen
Es gibt eine weitere Regel für Grenzwerte. Diese betrifft die Komposition von Funktionen.
Definition 1
Es seien \(f\) und \(g\) Funktionen und \(f\) sei auf dem Wertebereich der Funktion \(g\) definiert. Die Komposition \( (g \circ f ) \) der Funktionen \( g \) und \( f \) entsteht durch Anwendung der Funktion \(g\) auf das Ergebnis der Funktion \(f\):
\[ (g \circ f)(x) = g(f(x)) \]

Beispiele
Die Definitionsmenge der nachfolgenden Funktionen sei jeweils \(\mathbb{R}\).
Beispiel 4.
Falls \(f(x) = x^2\) und \(g(x) = x+2\), dann gilt:
-
\( (g \circ f)(x) = g(f(x)) = x^2 +2 \)
-
\( (f \circ g)(x) = f(g(x)) = (x+2)^2 = x^2 + 4x + 4 \)
Beispiel 5.
Für \(h(x) = x^3 + 4 \) und \( t(x) = x^2 \) gilt:
-
\( (h \circ t)(x) = h(t(x)) = (x^2)^3 +4 = x^6 +4 \)
-
\( (t \circ h)(x) = t(h(x)) = (x^3 + 4)^2 = x^6 + 8x^3 + 16 \)
Bemerkung: Die Operation der Funktionenkomposition ist nicht kommutativ, d.h. es gilt im Allgemeinen \( (g \circ f)(x) \neq (f \circ g)(x) \). Dies erkennt man sofort aus den obigen Beispielen.
Das folgende Theorem wendet die Komposition von Funktionen an:

Satz 2.
Es seien \(f(x)\) und \(g(x)\) Funktionen, so dass \( f \colon X \to Y \), \( g \colon Y \to Z \), \( \lim \limits_{x \to x_0} f(x) = y_0 \), \( \lim \limits_{y \to y_0} g(y) = z_0 \) gilt. Dann gilt \[ \lim \limits_{x \to x_0} (g \circ f)(x) = z_0 \]
Beachte dabei, dass wir bei der Funktion \( g \) den Limes gegen den Grenzwert \( y_0 \) von \( f \) betrachten.
Beispiel 6.
Wir wollen den Grenzwert der Funktion \( x \mapsto e^{\frac1x} \) gegen \( 0 \) betrachten.
Zunächst suchen wir die "innere" Funktion \( f \) und "äußere" Funktion \( g \). Manchmal gibt es hierfür meherer Möglichkeiten, in unserem Fall sieht man schnell, dass die äußere Funktion \( g(x) = e^x \) ist und dementsprechend \( f(x) = \frac1x \), da dann \( (g \circ f)(x)= e^{\frac1x} \) gilt.
Nach Satz 2 müssen wir dann \( \lim \limits_{x\to0}(f(x)) = \lim \limits_{x\to0}(\frac1x) \) bestimmen. Da es bei \( \frac1x \) einen Unterschied macht, ob man von links oder rechts gegen die \( 0 \) geht, machen wir eine Fallunterschiedung (d.h. die Ausgangsfrage ist "doof" gestellt).
Von links: \( \lim \limits_{x\to0^-}f(x) = \lim \limits_{x\to0^-} \frac1x = - \infty \)
Wir müssen nun \( g(x) \) gegen diesen Wert "laufen" lassen:
\( \lim \limits_{x\to -\infty}g(x) = \lim \limits_{x\to - \infty} e^x = 0 \)
Gesamt folgt \( \lim \limits_{x\to 0^-} e^{\frac1x} = 0 \)
Von rechts: \( \lim \limits_{x\to0^+} f(x) = \lim \limits_{x\to0^+} \frac1x = \infty \)
Wir müssen nun \( g(x) \) gegen diesen Wert "laufen" lassen:
\( \lim \limits_{x\to \infty} g(x) = \lim \limits_{x\to \infty} e^x = \infty \)
Gesamt folgt \( \lim \limits_{x\to 0^+} e^{\frac1x} = \infty \)
Beispiel 7.
Es soll der Grenzwert der Funktion \( x \mapsto \sin( e^x ) \) gegen \( - \infty \) bestimmt werden.
Hier ist die "äußere" Funktion \( g(x) = sin(x) \) und die "innere" Funktion muss \( f(x) = e^x \) sein, da somit \( (g \circ f)(x) = sin(e^x) \) gilt.
Wir müssen nun also zuerst \( \lim \limits_{x\to - \infty}(f(x)) = \lim \limits_{x\to - \infty}(e^x) \) bestimmen. Da \( e^x \) sich gegen \( - \infty \) immer näher der \( 0 \) annähert, gilt \( \lim \limits_{x\to - \infty}(e^x) = 0 \).
Nach Satz 2 müssen wir jetzt \( g(x) \) gegen den Grenzwert \( 0 \) betrachtet werden. Also benötigen wir \( \lim \limits_{x\to0}(g(x)) = \lim \limits_{x\to0}(sin(x)) = 0 \).
Es gilt also \( \lim \limits_{x\to - \infty}(g \circ f)(x)) = \lim \limits_{x\to0}(g(x)) = \lim \limits_{x\to0}(sin(x) = 0 \).
Beispiel 8.
Die Funktion \( x \mapsto \frac1{x^3 + 1} \) soll an dem Grenzwert \( -1 \) betrachtet werden.
Hier ist die "äußere" Funktion \( g(x) = \frac1x \). Die "innere" Funktion ist in diesem Fall \( f(x) = x^3 + 1 \). Also gilt \( (g \circ f)(x) = \frac1{x^3-1} \).
Nach Satz 2 muss zuerst der Grenzwert von \( f \) betrachtet werden. Wir brauchen also zuerst \( \lim \limits_{x\to-1}(f(x)) = \lim \limits_{x\to-1}(x^3 + 1) \). Da \( f \) ein Polynom dritten Grades ist, geht \( f \) an dem Grenzwert \( -1 \) gegen \( (-1)^3 + 1 = 0 \).
Es gilt also \( \lim \limits_{x\to-1}(f(x)) = \lim \limits_{x\to-1}(x^3 + 1) = 0 \).
Im nächsten Schritt wird der Grenzwert von \( g \) gegen den Grenzwert von \( f \), also \( 0 \) betrachtet. Hier ist allerdings nicht festgelegt, von welcher Seite aus man den Grenzwert annähert, also müssen wir uns beide Möglichkeiten getrennt anschauen.
Von links:
\( \lim \limits_{x\to0^-}(g(x)) = \lim \limits_{x\to0^-}(\frac1x) = - \infty \)
Es gilt also \( \lim \limits{x\to-1^-}(g \circ f)(x) = \lim \limits_{x\to-1^-}( \frac1{x^3 + 1}) = \lim \limits_{x\to0^-}(g(x)) = \lim \limits_{x\to0^-}(\frac1x) = - \infty \).
Von rechts:
\( \lim \limits_{x\to0^+}(g(x)) = \lim \limits_{x\to0+}(\frac1x) = + \infty \)
Dadurch folgt \( \lim \limits_{x\to-1^+}(g \circ f)(x) = \lim \limits_{x\to-1^+}(\frac1{x^3 + 1}) = \lim \limits_{x\to0^+}(g(x)) = \lim \limits_{x\to0^+}(\frac1x) = + \infty \).




4.3. Stetigkeit

Definition und anschauliches Stetigkeitskonzept
In diesem Abschnitt wird eine wesentliche Eigenschaft von Funktionen eingeführt, nämlich die Stetigkeit. Stetig kann eine Funktion an einer Stelle oder in einer Menge sein. Viele Konzepte und Sätze gelten nur für stetige Funktionen. Beispielsweise ist die Stetigkeit einer Funktion dafür notwendig, um die Ableitung dieser Funktion berechnen zu können (Ableitungen werden im nächsten Modul dieses Kurses behandelt). Ein tiefes Theorem, das nach den Mathematikern Marshall H. Stone und Karl Weierstraß benannt wurde, besagt, dass man jede stetige Funktion auf einem abgeschlossenen Intervall beliebig gut durch geeignete Polynome annähern kann.
Eine einfache intuitive Erklärung für stetige Funktionen ist die folgende:
Eine Funktion wird man natürlicher Weise stetig nennen wenn man den Graph einer Funktion ohne abzusetzen zeichnen kann. Aber diese einfache Erklärung erläutert nicht vollständig den Begriff "Stetigkeit" (und ist bei nicht zusammenhängender Definitionsmenge sogar falsch). Betrachten wir die Funktionen \(f(x) = \frac{1}{x}\) und \(g(x) = \tan (x)\). Sind sie in ihrem jeweiligen Definitionsbereich stetig? Sind sie sogar auf \(\mathbb{R}\) stetig? Um diese Fragen zu beantworten, benötigen wir die mathematische Definition der Stetigkeit.

Definition 1 (Stetigkeit einer Funktion)
Eine Funktion \(f\colon S\to \mathbb{R}\) heißt stetig an einer Stelle \(x_{0}\in S\), falls \[\lim_{x\to x_{0}}f(x)=f(x_{0})\]gilt. Eine Funktion \(f\colon S\to \mathbb{R}\) ist stetig, falls sie an jedem Punkt \(x_{0}\in S\) ihrer Definitionsmenge stetig ist.
Liest man diese Definition gewissenhaft, so erkennt man, dass für eine an der Stelle \(x_0\) stetige Funktion \(f(x)\) drei Eigenschaften erfüllt sein müssen:
-
\(f(x_0)\) ist definiert
-
\(\lim\limits_{x \to x_0} f(x)\) existiert
-
\(\lim\limits_{x \to x_0} f(x)\) hat den gleichen Wert wie \(f(x_0)\)
Beispiel 1.
Die Funktionen \(f(x) = x\), \(g(x) = |x|\) und \(h(x) = c\) (wobei \(c\) eine Konstante ist) sind stetig auf \(\mathbb{R}\).
Dies ergibt sich aus dem Folgenden: man wählt eine Stelle \(x_0\) und eine Folge \( \left( x_k \right)_{k \in \mathbb{N}} \), die gegen \(x_0\) konvergiert. Dann gilt:
-
\( \lim\limits_{k \to \infty} f(x_k) = \lim\limits_{k \to \infty} x_k = x_0 = f(x_0) \)
-
\( \lim\limits_{k \to \infty} g(x_k) = \lim\limits_{k \to \infty} |x_k| = |x_0| = g(x_0) \)
-
\( \lim\limits_{k \to \infty} h(x_k) = \lim\limits_{k \to \infty} c = c = h(x_0) \)
Die oben aufgefühten Ergebnisse ergeben sich direkt aus der Anwendung der Definition stetiger Funktionen. Daher sind alle drei Funktionen \(f(x) = x\), \(g(x) = |x|\) und \(h(x) = c\) stetig an jeder Stelle der Menge \(\mathbb{R}\).

Satz 1.
Summe, Produkt und Differenz von an einer Stelle stetigen Funktionen sind an dieser Stelle ebenfalls stetig. Wenn \(f\) und \(g\) stetig sind an der Stelle \(x_0\) und \(g(x_0) \neq 0\) gilt, so ist \( \frac{f}{g}(x) \) auch stetig an der Stelle \(x_0\).
Bemerkung: Aus diesem Satz und Beispiel 1 folgt, dass alle Polynome auf \(\mathbb{R}\) stetig sind.

Satz 2.
Die Komposition zweier stetiger Funktionen ist wiederum eine stetige Funktion.

Unstetigkeitsstellen
Stetige Funktionen spielen eine wichtige Rolle in Mathematik, Naturwissenschaften und Technik. Aber nicht jede Funktion ist stetig. Wenn eine Funktion nicht stetig an einer Stelle ihres Definitionsbereichs ist, so heißt die Funktion an dieser Stelle unstetig und die Stelle eine Unstetigkeitsstelle. Es gibt verschiedene Arten von Unstetigkeitsstellen. Diese werden wir nachfolgend klassifizieren.
In der Definition der Stetigkeit können verschiedene Bedingungen verletzt sein. Jede dieser Verletzungen führt zu einer Unstetigkeitsstelle. Für die nachfolgende Klassifikation nehmen wir an, dass die Funktion \(f\) in einer Umgebung des Punktes \(x_0\) definiert, jedoch nicht stetig an der Stelle \(x_0\) ist.
Hebbare Unstetigkeit
Eine Unstetigkeitsstelle heißt hebbar, falls die einseitigen Grenzwerte \(\lim\limits_{x \to x_0^-} f(x)\) und \(\lim\limits_{x \to x_0^+} f(x)\) existieren, endlich und gleich sein, jedoch nicht mit dem Wert \(f(x_0)\) übereinstimmen. Eine solche Funktion kann an der Unstetigkeitstelle so umdefiniert werden kann, dass sie stetig wird.
\[ \lim\limits_{x \to x_0} f(x) \neq f(x_0) \]
Im folgenden führen wir das an einem Beispiel aus:
Gegeben sei die folgende Funktion (der Graph ist auf der rechten Seite):
\[ f(x) = \left\{ \begin{array}{lr} x^2, & \text{für } x < 1\\ 0, & \text{für } x = 1\\ 2-x, & \text{für } x > 1 \end{array} \right. \]Es gilt:
\(\lim\limits_{x \to x_0^-} f(x)=1\) und \(\lim\limits_{x \to x_0^+} f(x)=1\)
Aber:
\[ \lim\limits_{x \to x_0} f(x) =1\neq 0= f(x_0) \]
Die Funktion \(f(x)\) hat an der Stelle \(x_0 = 1\) eine hebbare Unstetigkeit, da diese entsprechend umdefineirt werden kann. In unserem Fall genügt es, \(f(1)=1\) zu setzen um die Funktion \(f(x)\) stetig auf ganz \(\mathbb{R}\) zu machen.
Die abgeänderte Funktion hat dann folgende Vorschrift:
\[ f_{neu}(x) = \left\{ \begin{array}{lr} x^2, & \text{für } x<1\\ 1, & \text{für } x=1\\ 2-x, & \text{für } x>1 \end{array} \right. \]
Sprungstelle
Betrachten wir die Kostenfunktion \(C(t)\) für einen Parkplatz über die Zeitdauer \(t\). Wenn wir annehmen, dass das Parken für jede angefangene Stunde 2€ kostet, sieht der Funktionsgraph wie rechts dargestellt aus.
An ganzzahligen Stellen \(t=1\), \(t=2\), \(t=3\), ... tritt ein Sprung auf. Beispielsweise ergibt sich für \(t=1\):
\[ \lim\limits_{t \to 1^-} c(t) = 2 \neq 4 = \lim\limits_{t \to 1^+} c(t) \]Daher existiert der Grenzwert \(\lim\limits_{t \to 1} c(t)\) nicht und daher sind die Stetigkeitsbedingungen nicht erfüllt.
Um eine Unstetigkeitsstelle \(x_0\) als Sprungstelle zu identifizieren (Unstetigkeitsstelle erster Ordnung) müssen die beiden einseitigen Grenzwerte existieren und endlich sein, jedoch nicht gleich. An der Stelle \(x_0\) kann die Funktion einen beliebigen (reellen) Wert annehmen.
Polstellen und wesentliche Unstetigkeiten
Um die Bedingungen der Stetigkeit zu verletzen ist es möglich, dass ein einseitiger Grenzwert nicht existiert oder nicht endlich ist. Dazu betrachte wir die folgende Funktion \(g\):
\[ g(x) = \left. \begin{cases} \sin \frac{5}{x-1}, & \text{für } x < 1\\ 0, & \text{für } x = 1\\ \frac{1}{x-1}, & \text{für } x > 1 \end{cases} \right. \]Der linksseitige Grenzwert \(\lim\limits_{x \to 1^-} g(x)\) existiert nicht und der rechtsseitige Grenzwert \(\lim\limits_{x \to 1^+} g(x)\) ist nicht endlich. Daher liegt an der Stelle \(x_0 = 1\) linksseitig eine wesentliche Unstetigkeit und rechtsseitig eine Polstelle vor.

Übung 1.
Hat die Funktion \[f(x)=\frac{1}{2^{\frac{1}{x^2}}}\] mit \(\mathbb{D}_f=\mathbb{R}\backslash\{0\}\) eine hebbare Definitionslücke?
4.4. Eigenschaften stetiger Funktionen

Eigenschaften stetiger Funktionen
Dieser Anschnitt beinhaltet einige wichtige Eigenschaften stetiger Funktionen. Wir starten mit dem Zwischenwertsatz (Satz von Bolzano). Dieser Satz besagt, dass eine Funktion, wenn sie auf einem (abgeschlossenen) Intervall stetig ist, jeden Funktionswert zwischen den Funktionswerten an den Endpunkten annimmt. Intuitiv folgt das sofort aus der Tatsache, dass die Funktion \(f\) stetig auf dem Intervall ist.

Satz 1.
Es sei\(f(x) \colon \left[ a,b \right] \to \mathbb{R} \) eine auf ihrer Definitionsmenge stetige Funktion und \( f(a) < s < f(b) \). Dann gibt es eine Stelle \( x_0 \in \left[ a,b \right] \) mit \( f(x_0) = s \).
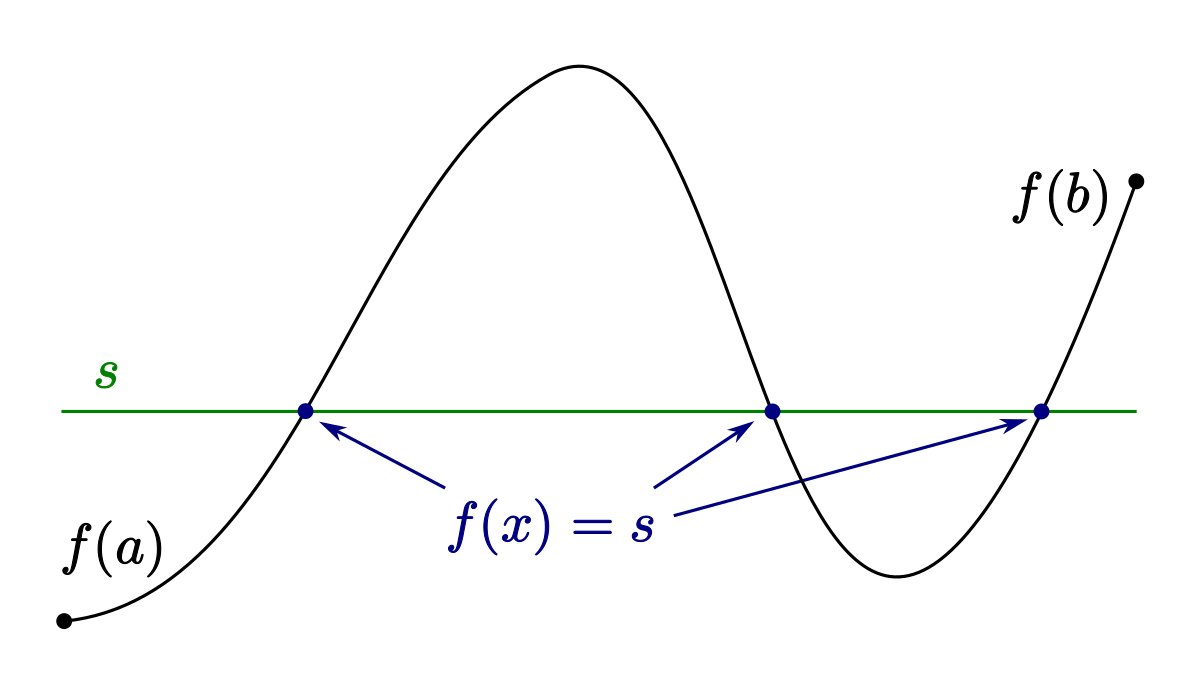
Beispiel 1.
Es sei \( f(x) \colon \mathbb{R} \to \mathbb{R} \) die Funktion \( f(x) = x^3 - 2x^2 + 3x - 4 \). Gibt es eine Stelle \( x_0 \), für die \( f(x) = 0 \) gilt?
Da \( f(x) \) ein Polynom ist, ist \(f\) stetig. Es gilt
\[ f(-10) = - 1000 - 200 - 30 - 4 = -1234 \]und
\[ f(10) = 1000 - 200 + 30 - 4 = 826 \]Aus dem Zwischenwertsatz folgt, dass es im Intervall \([-10,10]\) für jeden Wert \(s\) mit \( -1234 < s < 826 \) ein zugehöriges \( x \) mit \(f(x)=s\) existiert. Für \( s = 0 \) gibt es daher ein \( x_0 \) mit \( f(x_0) = 0 \).
Mit Hilfe dieses Satzes ist es jedoch nicht möglich, ein mögliches \( x_0 \) zu finden. Man weiß auf Grund des Satzes nur, dass ein solches \(x_0\) existiert.
Beispiel 2.
Gegeben sei die Temperatur am Nordpol und am "diametral entgegengesetzen" Punkt (dem Südpol). Die Differenz der Temperaturen sei \( \alpha \). Wir bewegen uns nun um die Erde vom Nord- zum Südpol und bestimmen die Temperaturdifferenz an jedem Punkt dieses Weges zum diametral entgegengesetzen Punkt. Wenn wir am Südpol angekommen sind, ist diese Differenz \(-\alpha\) (wir müssen uns dazu hinreichend schnell bewegen). Da die Temperaturänderung eine stetige Funktion ist, gibt es wenigstens einen Punkt auf unserem Weg, an dem die selbe Temperatur wie an dem diamentral entgegengesetzten Punkt vorliegt (also die Differenztemperatur \(0\) ist).
Beispiel 3.
Jedes Polynom ungeraden Grades hat wenigstens eine (reelle) Nullstelle
Es sei \(h(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0\) ein Polymon \(n.ten\) Grades, wobei \( n \) ungerade und \(a_n\not=0\) ist. Offensichtlich ist einer der Grenzwerte \(\lim\limits_{x\to\infty}h(x)\) und \(\lim\limits_{x\to-\infty}h(x)\) plus unendlich und einer minus unendlich (da die Funktion \(h\) ungeraden Grad hat). Wir erhalten also:
\[ \lim\limits_{x \to +\infty} \left( a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 \right) =\] \[ = \lim\limits_{x \to +\infty} x^n \cdot \left( a_n + a_{n-1} \cdot \frac{1}{x} + a_{n-2} \cdot \frac{1}{x^2} + \ldots + a_1 \cdot \frac{1}{x^{n-1}} + a_0 \cdot \frac{1}{x^n} \right) =\] \[ = \lim\limits_{x \to +\infty} \left( a_n x^n \right) = \begin{cases} +\infty \text{, when } a_n > 0 \\ -\infty \text{, when } a_n < 0 \end{cases} \]Analog streben die Werte von \( h(x) \) für \(x \to -\infty \) gegen \( -\infty \), falls \( a_n \) positiv und gegen \( +\infty \) für negatives \( a_n \). Daher gibt es in jedem Fall positive und negative Funktionswerte.
Da Polynome stetige Funktionen sind, folgt aus dem Zwischenwertsatz, dass die Funktion \( h\) wenigstens eine reelle Nullstelle hat.
Bemerkung: Die obige Aussage ist für Polynome geraden Grades im Allgemeinen falsch. Für gerades \( n \) sind die beiden Grenzwerte entweder plus unendlich oder minus unendlich und haben damit das gleiche Vorzeichen. Daher funktioniert die Idee von Beispiel 3 nicht in diesem Fall.

Satz 2.
Eine stetige Funktion \(f \colon \left[ a, b \right] \to \mathbb{R} \) ist beschränkt.

Bemerkung: Man beachte, dass die obige Aussage für offene Intervalle \( \left] a, b \right[ \) nicht gilt. Dazu betrachten wir die Funktion \( f(x) = \frac{1}{x} \) im Intervall \( \left] 0, 1 \right[ \). Wenn \(x\) von rechts gegen \(0\) strebt, so wird der Funktionswert \(f(x)\) beliebig groß. Also ist die Funktion zwar stetig, aber unbeschränkt auf \( \left] 0, 1 \right[ \).
Warum ist diese Eigenschaft so wichtig?
Beschränkte stetige Funktionen nehmen auf jedem abgeschlossenen Intervall \( \left[ a, b \right] \) ihr Maximum und Minimum an. Ferner bedeutet dies, dass die stetige Funktion \(f\) das abgeschlossene Intervall \( \left[ a, b \right] \) auf das abgeschlossene Intervall \( \left[ c, d \right] \) abbildet. Wir werden dies in Theorem 3 beweisen.

Satz 3.
Es sei \( f \colon \left[ a, b \right] \to \mathbb{R} \) eine stetige Funktion. Dann gibt es Werte \( c, d \in \left[ a, b \right] \), so dass \( f(c) \leq f(x) \leq f(d) \) für alle \( x \in \left[ a, b \right] \) gilt.


Numerisches Lösen
Neben dem graphischen Lösen gibt es verschiedene numerische Methoden, um näherungsweise Lösungen für Gleichungen zu finden. Numerische Methoden, sowie algebraische Methoden, werden oft zusammen mit Computern oder geeigneter Software angewandt, aber auch beim Benutzen der Software sollte man die Prinzipien der Methoden, auf denen die Algorithmen basieren, verstehen. Ebenso wichtig ist zu wissen, dass abhängig von der Methode das Ergebnis nur eine Nullstelle liefert, auch wenn die Gleichung mehrere Nullstellen besitzt
Unter den einfachsten numerischen Lösungsmethoden für Gleichungen ist das Intervallhalbierungs-Verfahren (Bisektion), welche auf dem Satz von Bolzano-Weierstraß basiert: wenn eine stetige Funktion negativ in einem Endpunkt eines Intervalls und positiv am anderen ist, dann muss es eine Nullstelle der Funktion irgendwo in diesem Intervall geben. Im Intervallhalbierungsverfahren wird das Intervall wiederholt halbiert, während das Vorzeichen der Funktion im Mittelpunkt eines Intervalls (oder nahe dem Mittelpunkt) überprüft wird.
Beispiel 3.
Lösungen der Gleichung
Lösen wir die Gleichung \[ 2^x - x -4 = 0, \] wobei \( x>0 \).
Leicht sieht man, dass die Gleichung, welche auch umgeschrieben werden kann als \[ 2^x = x+4, \] ihre einzige positive Nullstelle irgendwo zwischen den Punkten \( x=2 \) und \( x=3 \) hat. Dies kann zum Beispiel durch skizzieren der Kurve \( y=2^x \) und der Geraden \( y=x+4 \), veranschaulicht werden, siehe Bild unten. Tatsächlich ist das Bild sehr viel genauer als notwendig: eine grobe Skizze mit Stift und Papier sollte genügen.
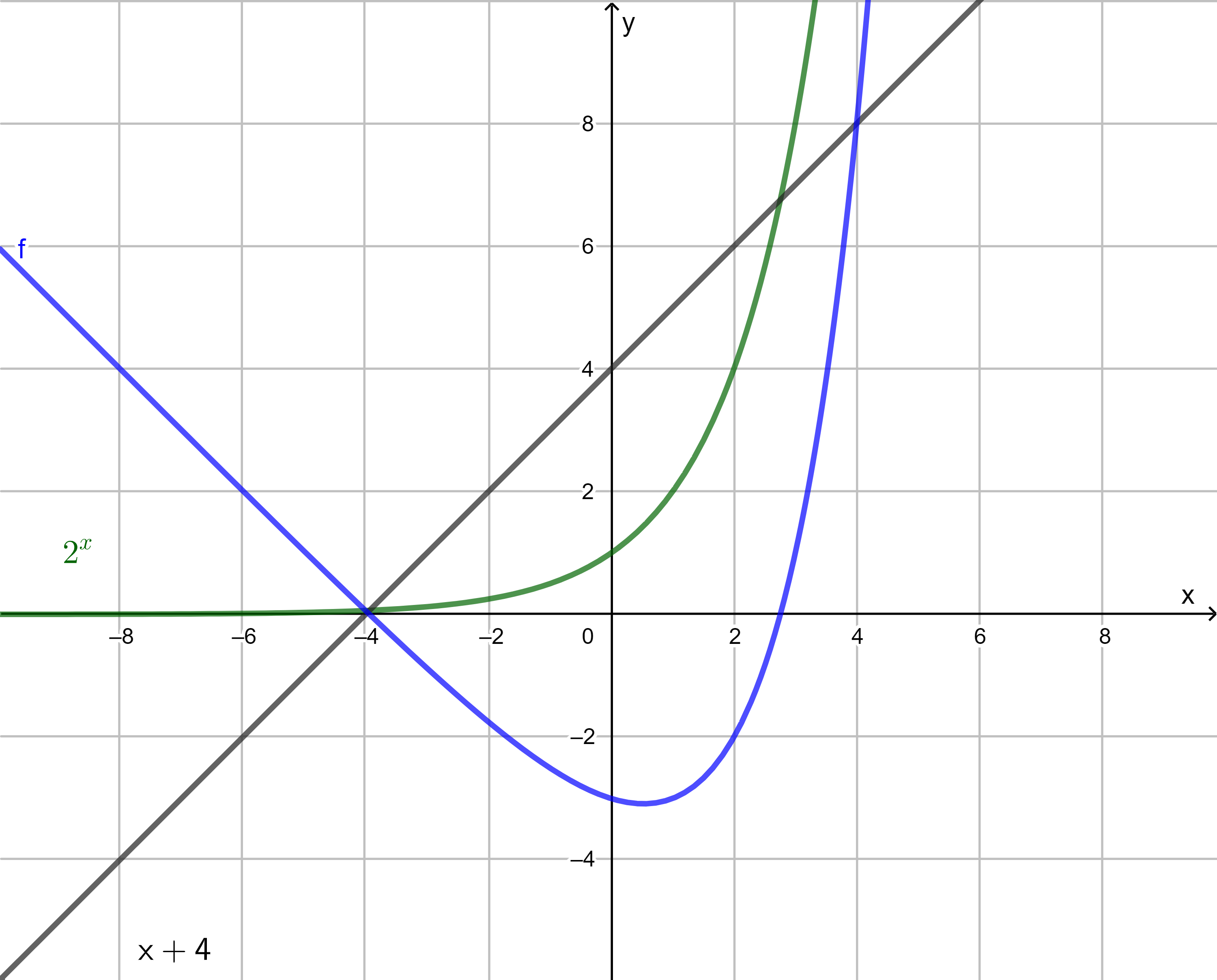
Nun kann die angenäherte Nullstelle wesentlich genauer bestimmt werden, indem Bisektion auf die Funktion angewandt wird \( f(x)=2^x-x-4 \):
- \( f(2) = -2 < 0 \) und \(f(3) = 1 > 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2 , 3[ \) (wie wir bereits wussten)
- \( f(2{,}5) \approx -0{,}84 < 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2{,}5 \hspace{0.1cm}; \hspace{0.1cm} 3[ \)
- \( f(2{,}75) \approx -0{,}02 < 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2{,}75 \hspace{0.1cm}; \hspace{0.1cm} 3[\)
- \( f(2{,}85) \approx 0{,}36 > 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2{,}75 \hspace{0.1cm}; \hspace{0.1cm} 2{,}85[ \)
Nun kennen wir die Nullstelle mit einer Genauigkeit von einer Nachkommastelle: \( x \approx 2{,}8 \).
Das Intervallhalbierungsverfahren ist nicht sehr effizient: wenn eine höhere Genauigkeit notwendig ist, kann die Zahl der Bisektionen sehr groß sein. Es gibt effizientere und raffiniertere numerische Lösungsmethoden, wie das Newton-Verfahren. Wie oben zu sehen ist, kann graphisches Lösen in Verbindung mit numerischem Lösen angewandt werden: erstmal eine sehr grobe Abschätzung für eine Nullstelle graphisch finden und dann die Abschätzung durch numerischen Methoden verfeinern.

Übung 1.
Die Gleichung \[ x^3+\ln x = 0 \] hat eine Lösung im Intervall \( [0,5 ; 1] \). Bestimme die Nullstelle auf zwei Nachkommastellen genau mithilfe des Intervallhalbierungsverfahrens.

4.5. Funktionen mehrerer Veränderlicher


Funktionen, die von mehr als einer Variablen oder Veränderlichen abhängen, nennt man Funktionen mehrerer Veränderlicher. Das einfachste Beispiel sind Funktionen mit zwei Variablen.
Der Definitionsbereich \(D\) von Funktionen zweier Veränderlicher ist eine Teilmenge der x-y-Ebene. Jedem Punkt \((x_0,y_0) \in D\) dieser Ebene wird ein Wert \(z_0= f(x_0,y_0)\) zugeordnet. Im Raum lässt sich dieser Zusammenhang durch einen Punkt mit den Koordinaten \((x_0, y_0,z_0)\) darstellen; man erhält so eine Fläche im Raum als Funktionsgraphen.
Formal wird eine Funktion zweier Veränderlicher wie folgt beschrieben:
\(f: D \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}\)
\((x,y) \rightarrow f(x,y)\)
Wir stellen uns ein dreidimensionales Koordinatensystem vor. Jedem Punkt \((x_1,y_1)\) der x-y-Ebene ordnen wir den Punkt \((x_1,y_1,z_1)\) mit \(z_1 = x_1 \cdot y_1\) zu.
Für jedes feste \(x\) ergibt sich eine Geradengleichung:
\(z = const. \cdot y\)
Für \(x = 2\) erhält man beispielsweise \(z = 2 \cdot y\). Diese Gleichungen beschreiben eine Gerade, die parallel zur y-z-Ebene verläuft. Analog gilt dies für jede Gleichung \(z = const. \cdot y\).
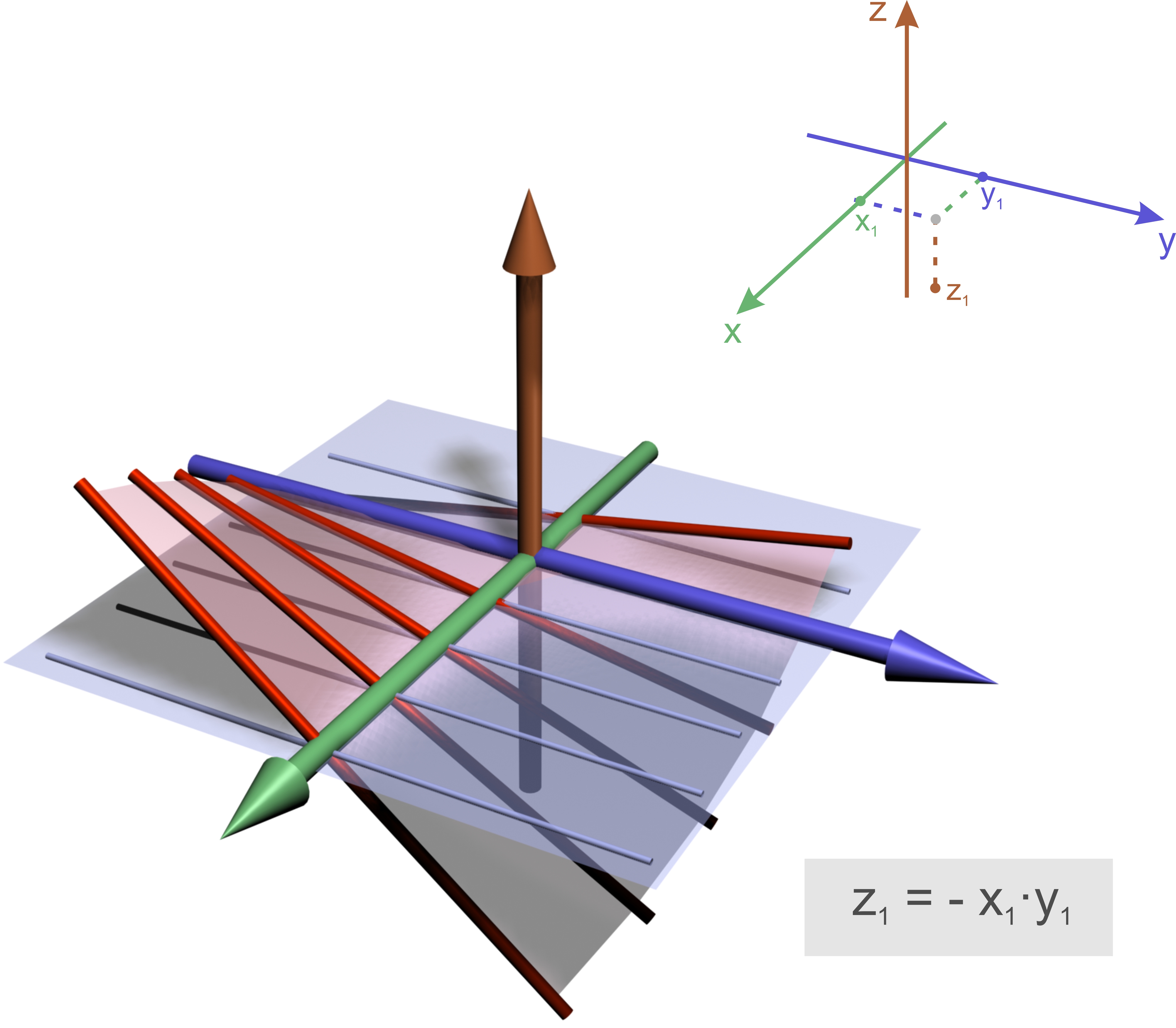 |
 |
Für variables \(x\) erhält man eine Geradenschar; sie erzeugt eine Fläche, die sog. Sattelfläche.
Wir betrachten die Funktion mit \(f (x,y) = x^2 + y^2\).
Man erkennt die Parabeln auf dieser Fläche, wenn man sich bei der Funktionsgleichung jeweils \(x\) oder \(y\) konstant denkt.

Wir betrachten die Funktionsgleichung
\(z(x,y) = 2x + 5y\)
Begründen Sie, warum der Graph der Funktion eine Ebene darstellt, indem Sie sich für den x-Wert (bzw. den y-Wert) nacheinander feste Werte z. B. \(x = \{-2,-1, 0, 1, 2\}\) eingesetzt denken.
\(f_a(x) = f (a, x) = a \cdot x^2\)
Hier fasst man Variable \(x\) und Scharparameter \(a\) als die beiden Variablen der Funktion zweier Veränderlicher auf.
Weitere Beispiele: \(f_a(x) = a \cdot \sin(x)\) wird als \(f(a,x) = a \cdot \sin(x)\) bzw. als \(f(x,y) = y \cdot \sin(x)\) aufgefasst.
In der Abbildung rechts ist der Graph der Funktion \(z = a \cdot x^2\) für \(a = \{-2, \ldots, 2\}\) gezeichnet.

Die Gleichung
\((\sqrt{x^2 + y^2} - R)^2 + z^2 - r^2 =0\)
beschreibt einen sog. Torus. Diesen kann man sich entstanden denken als einen Kreis vom Radius \(r\), der im Abstand \(R\) um die z-Achse rotiert. Die z-Achse ist Symmetrieachse, die x-y-Ebene Symmetrieebene des Torus.
Allerdings ist diese Fläche kein Graph einer Funktion, da es Punkte \((x_0,y_0)\) der Ebene unter dem Torus gibt, denen zwei z-Werte zugeordnet sind (was bei einer Funktion nicht sein kann). Um einen Funktionsgraphen zu erhalten, muss man entweder die obere (\(z \ge 0\)) oder die untere (\(z \le 0\)) Hälfte des Torus auswählen.
Der Graph der Funktion
\( z = C \cdot e^{-a^{2}(x^2 + y^2)}\)
mit Konstanten \(a,C \in \mathbb{R}\) ähnelt einer Glocke. Er ist rotationssymmetrisch bezüglich der z-Achse. Für konstante x- oder y-Werte erhält man die Gaußsche Glockenkurve, die in der Statistik die Normalverteilung charakterisiert.

4.6. Kurven und Abbildungen


Eine parametrisierte Kurve \(K\) ist eine Abbildung der Form
\( K:[a,b] \rightarrow \mathbb{R}^2\)
\(t \rightarrow (K_1(t),K_2(t)) = (x(t),y(t))\)
wobei \(t \in [a,b] \subset \mathbb{R}\); man nennt \(t\) den Parameter.
Die implizite Darstellung einer Kurve \(K\) erhält man als die Nullstellenmenge einer Gleichung:
\(K:\{(x,y) | f(x,y) = 0\}\)

Die Gerade \(g\) durch die Punkte \(A = (-1,1)\) und \(B = (-3,4)\) besitzt folgende Parameterdarstellung:
\((x = - 1 + t(- 3 - (- 1)), y = 1 + t(4 - 1))\)
also \((x = - 1 - 2t, y = 1 + 3t)\).
Die Parameterdarstellung ist dabei allgemein von der Form:
\(x = x_1 + t(x_2 - x_1), y = y_1 + t(y_2 - y_1)\), für alle \(t \in \mathbb{R} \)
In impliziter Form wird die Gerade \(g\) durch eine Gleichung ausgedrückt:
\((4 - 1)(x - (- 1)) = (- 3 - (- 1))(y - 1)\)
also \(3x + 2y + 1 = 0\)
Dies ergibt sich aus der allgemeinen Form
\((y - y_1) = m \cdot (x - x_1)\)
Darin ist \(m \in \mathbb{R}\) die sog. Steigung der Geraden, die sich per
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
berechnen lässt.
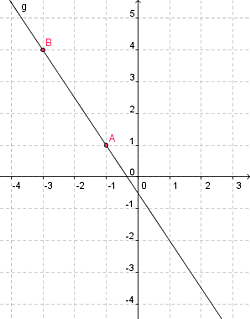

Ein Kreis ist die Menge aller Punkte \(P\), die von einem vorgegebenen Punkt \(M\) einen festen Abstand \(r\) haben, also
\(\{P \mid |P M | = r\}\)
Der Kreis ist durch die Angabe des Punktes \(M\), seines Mittelpunktes, und seines Radius’ \(r\) vollständig bestimmt.
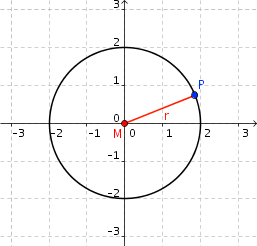
In impliziter Form lässt sich ein Kreis um den Nullpunkt \(M = (0, 0)\) mit dem Radius \(r = 2\) schreiben als
\(x^2 + y^2 = 2^2\)
Alternativ, aber äquivalent hierzu, lässt sich ein Kreis auch in Parameterform darstellen:
\((2 \cdot \cos(t), \,2 \cdot \sin(t)), 0 \le t < 2\pi \)

Der Kreis (rot) ist ein Spezialfall der Ellipse (blau) (vgl. Animation).

Eine Ellipse ist die Menge aller Punkte \(P\), deren Abstandssumme von zwei gegebenen Punkten \(F_1\) und \(F_2\), den sog. Brennpunkten, konstant ist. Also
\(\{P \mid |P F_1| + |PF_2| = const.\}\)
Hier sehen Sie die sog. Gärtnerkonstruktion einer Ellipse. Ziehen Sie mit der Maus am roten Punkt \(P\) und verändern Sie die Lage der Brennpunkte \(F_1\) und \(F_2\) mit dem orangen Schieberegler:
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} =1\)
Dies ist die Ellipsengleichung für eine Ellipse mit Mittelpunkt \((0, 0)\) in kartesischen Koordinaten. Die Parameterform dazu lautet:
\((a \cdot \cos(t), b \cdot \sin(t)), 0 \le t < 2\pi\)
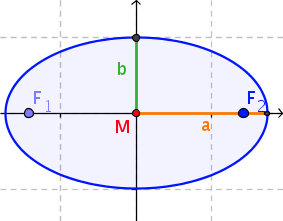
Wenn ein Rad vom Radius \(r\) auf einer ebenen Fläche entlang rollt (z. B. ein Autoreifen) ohne dabei zu gleiten und dabei die Bewegung eines Punktes \(P\) auf dem Rad aufgezeichnet wird (z. B. die Bewegung des Ventils), dann ist die Bahnkurve des Punktes \(P\) eine sog. Zykloide.
Als Parameter wählt man hier den Abstand \(a = |MP|\) von Mittelpunkt \(M\) des Rades zum betrachteten Punkt \(P\) und den sog. Wälzwinkel \(t\). Die Parameterdarstellung der Kurve lautet dann:
\((r \cdot t - a \cdot \sin(t), r - a \cdot \cos(t))\)
Abhängig von der Lage des Punktes \(P\) erhält man verschiedene Typen von Zykloiden: Wenn \(a = r\) heißt die Kurve gewöhnliche Zykloide, wenn \(a > r\) verschlungene Zykloide und sonst (\(a < r\)) gestreckte Zykloide.


4.7. Aufgaben


Aufgabe 1: Spirale
Zeichnen Sie die Kurve \(K(t) = (t \cdot \cos(t), t \cdot \sin(t))\) für \(0 < t < 20\). Die Kurve lässt sich aus einer Bewegung entstanden denken und dynamisch interpretieren, indem \(t\) als Zeit verstanden wird. Man nennt diese Kurve Spirale.
- Beschreiben Sie diese Bewegung!
- Geben Sie die Gleichung für die abgebildeten Spirale an!
Gegeben ist eine Ellipse \(E(x,y): \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\); \(a,b \in \mathbb{R}^+\). Geben Sie die Gleichung der Tangente an die Ellipse im Ellipsenpunkt \(P(x_0,y_0)\) an.
Hinweis: Gehen Sie vom Kreis \(K_a: x^2+ y^2= a^2\) aus und erzeugen Sie \(E\) durch eine Streckung bzw. Stauchung von \(K_a\) mit dem Faktor \(\frac{b}{a}\) parallel zur y-Achse. Gehen Sie dann von einer Kreistangente aus.
Es gibt verschiedene Möglichkeiten, ein Herz mit Hilfe von mathematischen Funktionen zu zeichnen. Insbesondere kann ein Herz sehr unterschiedliche Formen besitzen. Zeichnen Sie aus Funktionsstücken (mit GeoGebra) ein Herz. Das Bild rechts zeigt eine Möglichkeit der Umsetzung.
- Beschreiben Sie den Graphen \(G\) der Funktion mit \(f(x,y) = x^2+ y^2\), indem Sie \(G\) mit ausgewählten Ebenen schneiden und die Schittfiguren beschreiben.
- Wir betrachten die beiden Ebenen im Raum mit \(f(x,y) = 4x + y + 3\) und \(g(x,y) = -x + 3y - 5\) in einem gemeinsamen Koordinatensystem. Zeigen Sie, dass die beiden Ebenen zueinander senkrecht sind.
Aufgabe 5:
Die Gleichung \[ x^3+\ln x = 0 \] hat eine Lösung im Intervall \( [0,5 ; 1] \). Bestimme die Nullstelle auf zwei Nachkommastellen genau mithilfe des Intervallhalbierungsverfahrens.

5. Differentialrechnung


- Grundlagen zur Differentialrechnung
- Herleitung von bestimmten Ableitungen
- Ableitungsregeln
- Kurvendiskussion

5.1. Grundlagen

Definition

Ableitung - Definitionen und Grundlagen
Als nächstes folgt die Definition der Ableitung einer Funktion. Hierbei starten wir mit einem Beispiel, um die Idee hinter der formalen Definition zu veranschaulichen
Beispiel 0:
Der folgende Graph gibt an, wie weit ein Fahrradfahrer von seinem Startpunkt aus gelangt.
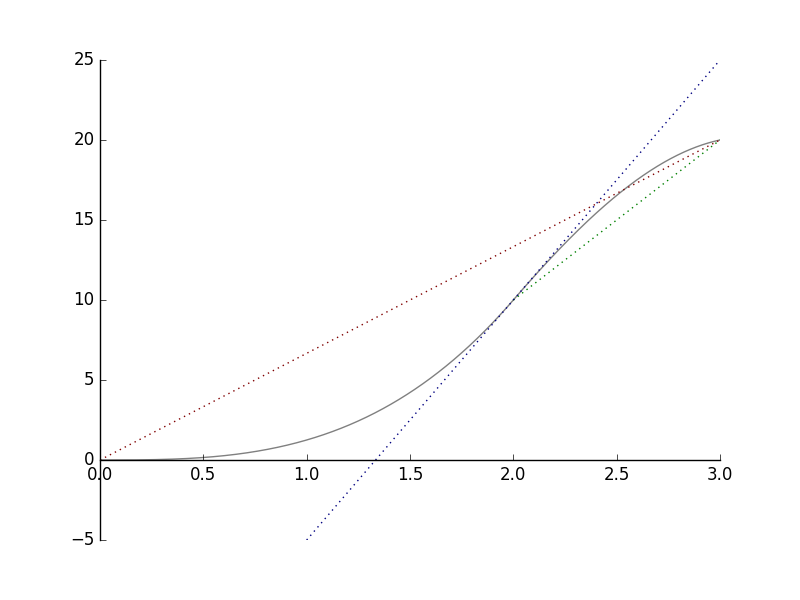
- Betrachte die rote Linie. Man erkennt, dass der Radfahrer innerhalb von 3 Stunden \(20\) km zurücklegt. Die durchschnittliche Geschwindigkeit der gesamten Strecke beträgt \(6.6\) km/h.
- Betrachte nun die grüne Linie. Innerhalb der zweiten und dritten Stunde legt der Radfahrer weitere \(10\) km zurück. Somit ist in diesem Zeitintervall die durchschnittliche Geschwindigkeit \(10\) km/h.
Hierbei betragen die Steigung der roten Linie \(\frac{20}{3} \approx 6.6\) und die Steigung der grünen Linie \(10\). Diese Werte entsprechen den zugehörigen Durchschnitts-Geschwindigkeiten. - Betrachte noch die blaue Linie. Sie ist die Tangente der Kurve im Punkt \(x=2\) h. Durch Anwendung des gleichen Prinzips wie mit durchschnittlichen Geschwindigkeiten, schließen wir, dass 2 Stunden nach der Abfahrt, die Geschwindigkeit der Radfahrers \(\frac{30}{2}\) km/h \(= 15\) km/h betrug.
Führt man diesen Gedankengang ins unendlich Kleine fort, dann kommt man zur allgemeinen Definition der Ableitung:

Definition 1 (Ableitung)
Sei \((a,b)\subset \mathbb{R}\). Die Ableitung der Funktion \(f\colon (a,b)\to \mathbb{R}\) im Punkt \(x_0\in (a,b)\) ist definiert als \[f'(x_0):=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}.\] Wenn \(f'(x_0)\) existiert, dann heißt \(f\) differenzierbar im Punkt \(x_0\).
Bemerkung: Da \(x = x_0+h\), folgt \(h=x-x_0\), und somit kann die Definition auch in der äquivalenten Form \[f'(x_0):=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}\] geschrieben werden.
Es gibt verschiedene Möglichkeiten die Ableitung zu notieren:
\[f'(x_0)=Df(x_0) =\left. \frac{df}{dx}\right|_{x=x_0}, \ \ f'=Df =\frac{df}{dx}. \]
Geometrische Interpretation
Betrachte die Kurve \(y = f(x)\). Legt man eine Gerade durch die Punkte \((x_0,f(x_0))\) und \((x_0+h, f(x_0+h))\), so beträgt die Steigung der Kurve \[\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0} = \frac{f(x_0+h)-f(x_0)}{h}.\] Wenn \(h \to 0\) definieren wir den Grenzfall als Tangente in diesem Punkt. Die Gerade berührt die Kurve \(y = f(x)\) nur im Punkt \((x_0, f(x_0))\). Die Gerade ist die Tangente an die Kurve \(y=f(x)\) im Punkt \((x_0,f(x_0))\) und ihre Steigung beträgt \[\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h},\] welches der Ableitung der Funktion \(f\) im Punkt \( x_0\) entspricht. Somit ist die Tangente durch die Gleichung \[y=f(x_0)+f'(x_0)(x-x_0)\] gegeben.
Interaktivität. Manipuliere die Werte für \(x_0\) und betrachte die Änderungen der Tangente an der Kurve.
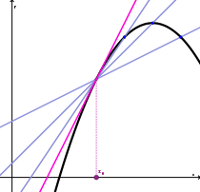
geometrische Interpretation
Beispiel 1:
Sei \(f\colon \mathbb{R} \to \mathbb{R}\) die Funktion \(f(x) = x^3 + 1\). Die Ableitung von \(f\) in \(x_0 = 1\) beträgt: \[\begin{aligned}f'(1) &=\lim_{h \to 0} \frac{f(1+h)-f(1)}{h} \\ &=\lim_{h \to 0} \frac{(1+h)^3 + 1 - 1^3 - 1}{h} \\ &=\lim_{h \to 0} \frac{1+3h+3h^2+h^3-1}{h} \\ &=\lim_{h \to 0} \frac{h(3+3h+h^2)}{h} \\ &=\lim_{h \to 0} 3+3h+h^2 \\ &= 3. \end{aligned}\]
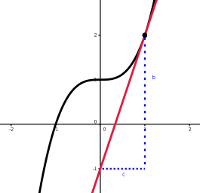
Die Funktion \( x^3 + 1\) und ihre Tangente im Punkt \(1\).
Beispiele zur elementaren Berechnung der Ableitung bei verschiedenen Funktionen
Beispiel 2:
Sei \(g\colon \mathbb{R} \to \mathbb{R}\) die Funktion \(g(x)=|x|\). Hat \(g\) eine Ableitung im Punkt \(0\)?
Nun ist \[g'(x_0)= \begin{cases}+1 & \text{wenn $x_{0}>0$} \\ -1 & \text{wenn $x_{0}<0$}\end{cases}\]
Der Graph \(y=g(x)\) hat keine Tangente im Punkt \(x_0=0\): \[\frac{g(0+h)-g(0)}{h}= \frac{|0+h|-|0|}{h}=\frac{|h|}{h}=\begin{cases}+1 & \text{für $h>0$}, \\ -1 & \text{für $h<0$}.\end{cases}\] Folglich existiert \(g'(0)\) nicht.
Ergebnis. Die Funktion \(g\) ist nicht differenzierbar im Punkt \(0\).
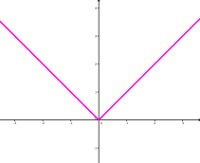
Die Funktion \(|x|\).
Bemerkung. Sei \(f\colon (a,b)\to \mathbb{R}\). Wenn \(f'(x)\) für jedes \(x\in (a,b)\) existiert, dann erhalten wir die Funktion \(f'\colon (a,b)\to \mathbb{R}\). Wir schreiben:
| (1) | \(f(x)\) | = \(f^{(0)}(x)\), | |
| (2) | \(f'(x)\) | = \(f^{(1)}(x)\) | = \(\frac{d}{dx}f(x)\), |
| (3) | \(f''(x)\) | = \(f^{(2)}(x)\) | = \(\frac{d^2}{dx^2}f(x)\), |
| (4) | \(f'''(x)\) | = \(f^{(3)}(x)\) | = \(\frac{d^3}{dx^3}f(x)\), |
| ... |
Hier ist \(f''(x)\) die zweite Ableitung von \(f\) in \(x\), \(f^{(3)}\) ist die dritte Ableitung und so weiter.
Wir führen folgende Notation ein: \begin{eqnarray} C^n\bigl( (a,b)\bigr) =\{ f\colon \, (a,b)\, \to \mathbb{R} & \mid & f \text{ ist } n \text{ mal differenzierbar im Intervall } (a,b) \nonumber \\ & & \text{ und } f^{(n)} \text{ ist stetig}\}. \nonumber \end{eqnarray} Diese Funktionen sind n-mal stetig differenzierbar.
Eine praktische Anwendung für höhere Ableitungen sehen Sie in Die Änderungsrate aus physikalischer Sicht und eine innermathematische Anwendung im späteren Kapitel Kurvendisskussion.

Linearisierung und Differenzial
Die Ableitung dient auch dazu Funktionen zu approximieren. Aus der Definition der Ableitung erhalten wir \[ f'(x_0)\approx \frac{f(x)-f(x_0)}{x-x_0} \Leftrightarrow f(x)\approx f(x_0)+f'(x_0)(x-x_0), \] wobei die rechte Seite die Linearisierung oder das Differenzial von \(f\) in \(x_0\) ist. Das Differenzial wird mit \(df\) bezeichnet. Der Graph der Linearisierung, \[ y=f(x_0)+f'(x_0)(x-x_0), \] ist die Tangente vom Graph der Funktion \(f\) im Punkt \((x_0,f(x_0))\). Später, in der Analysis mit mehreren Variablen, wird die tatsächliche Bedeutung des Differenzials klarer. Für das Erste, sind die genauen Details nicht notwendig. Dies motiviert eine äquivalente Definition der Ableitung:
\(f\) heißt differenzierbar an der Stelle \(x_0\), wenn eine Zahl existiert, sodass gilt:
\[ f(x) = f(x_0) + m\cdot (x-x_0) + r(x-x_0),\]
wobei für die Restfunktion \(r\) gilt:
\[ \lim\limits_{x \to x_0} \frac{ r(x-x_0)}{x-x_0} = 0 \]
\(m\) wird dann Ableitung von \(f\) an der Stelle \(x_0\) genannt; \(f'(x_0)=:m\).
Zur Vermeidung des Quotienten im Grenzwert lässt sich stattdessen auch definieren:
\[ f(x) = f(x_0) + m\cdot (x-x_0) + (x-x_0) \cdot R(x-x_0), \]
wobei
\[ \lim\limits_{x \to x_0} R(x-x_0) = 0 \]
Bedeutung der Definition:
Für lineare Funktionen lässt sich jeder Funktionswert \(f(x)\) aus dem Funktionswert an einer festen Stelle \(x_0\) berechnen, indem die Differenz \(x-x_0\) mit der Steigung \(m\in\mathbb{R}\) multipliziert wird:
\[f(x)=f(x_0) + (x-x_0)\cdot m.\]
Bei nichtlinearen Funktionen muss die Steigung in Abhängigkeit von der Stelle modifiziert werden, doch lokal passt die Approximation gut, sofern die Modifikation \(R(x-x_0)\) lokal klein ist und im Grenzwert verschwindet, d.h.:
\[ f(x) = f(x_0) + (x-x_0) \cdot (m + R(x-x_0)) \text{ mit } \lim\limits_{x \to x_0} R(x-x_0) = 0.\]

Anschauliche/graphische Beziehung zwischen Funktionsgraph und Ableitung
Graphisch differenzieren
Vom Verständnis der Ableitung als Tangentensteigung ausgehend kann ohne formale Berechnungs-Verfahren graphisch differenziert werden. Dazu muss an einzelnen Punkten des Graphen einer Funktion die Steigung ermittelt werden (z.B. durch Anlegen einer Tangente). Der (gemessene) Wert für deren Steigung wird als Ordinate (y-Wert) – gemeinsam mit der zugehörigen Abszisse (x-Wert) – als Punkt in ein (zweites) Koordinatensystem übertragen.
Verschieben Sie den Punkt A entlang des Graphen. Im linken Fenster wird der Wert der Tangentensteigung an diesem Punkt eingezeichnet.Vorstellungen
Es gibt verschiedene Möglichkeiten die Ableitung zu interpretieren:
Im folgenden betrachten wir die unterhalb der Definition beschriebene Interpretation die Ableitung als die Steigung der Tangenten an den Punkt einer differenzierbaren Funktion verstehen. Hierbei darf die Tangente aber - anders als beim Kreis - den Funktionsgraphen durchaus mehrmals schneiden wie das Beispiel rechts zeigt.
Vielmehr schmiegt sich die Tangente in diesem einen Punkt der Gerade an, wenn man beliebig weit hineinzoomt. Man kann sich deshalb besser eine Schmiegegerade statt einer Tangenten vorstellen.
Die Tangente und die Kurve im gemeinsamen Punkt haben dabei die gleiche Steigung. Zusätzlich kann man anhand der Kurve die "lokale Richtung" der Kurve ablesen. In obigem Fall steigt die Kurve in einer gewissen Steigung
Ableitung als lokale Änderungsrate
Betrachten wir nochmals das Beispiel 0, dann tauchen hier mehrere Arten von Änderungsraten auf (Der Graph sei durch die Funktion \( f \) gegeben). Die Angabe der insgesamt zurückgelegten Strecke von 20 km durch die Betrachtung der Differenz \( f(3) - f(0) \) ist eine absolute Änderungsrate. Berücksichtigt man zusätzlich die benötigte Zeit, indem man mittels Steigungsdreieck die Steigung bzw. mittlere Geschwindigkeit berechnet, so ist dies eine mittlere Änderungsrate. In unserem Fall war das der Differenzenquotient \( \frac{f(3)-f(0)}{3-0}=\frac{20}{3} \).
Verkleinert man systematisch das Intervall auf der \( x \)-Achse (in unserem Fall die Zeit), so erhält man die lokale Änderungsrate bzw. den Differentialquotienten aus der Definition der Ableitung. Dieser spiegelt nicht mehr die mittlere Geschwindigkeit, sondern die Momentantgeschwindigkeit in einem Punkt wider bzw. allgemeiner die Steigung einer Kurve in einem Punkt.
Wichtig ist dabei zu verinnerlichen, dass der Differenzenquotient ein Quotient und der Differentialquotient der Grenzwert eines Quotienten ist.
Ableitung als lokale lineare Approximation
Wir haben bereits gesehen, dass Graphen differenzierbarer Funktionen Schmiegegeraden besitzen. Wie man den Funktionsterm der Tangenten bestimmt, wurde unter Linearisierung und Differential bereits angesprochen. Wenn wir wieder das Beispiel aus der "Ableitung als Tangentensteigung" betrachten und noch viel weiter hineinzoomen würden, so könnten wir irgendwann kaum mehr zwischen Kurve und Tangente unterscheiden - der Graph der Kurve ist also für kleine Abweichungen des \( x \)-Wertes vom Schnittpunkt linear. Man kann also für diese \( x \)-Werte statt des möglicherweise komplizierten Funktionsterms der Kurve die einfachere Linearisierung als gute Näherung nutzen.
Diese Eigenschaft nutzt man z.B. bei der Kleinwinkelnäherung. Dabei können die trigonometrischen Funktionen Sinus, Kosinus und Tangens für Winkel nahe \( 0 \) linearisiert werden. So ist \( sin(x) \approx x \approx tan(x) \) sowie \( cos(x) \approx 1 \) für sehr kleine \(x\). Dies ist graphisch anschaulich, wenn man in den entsprechenden Graphen hineinzoomt, und kann z.B. mittels derer Taylor-Entwicklungen bewiesen werden.

5.2. Eigenschaften von Ableitungen

Eigenschaften von Ableitungen
In diesem Kapitel beschäftigen wir uns mit nützlichen Eigenschaften der Ableitung. Diese Eigenschaften erlauben es uns Ableitungen für einige bekannte Klassen von Funktionen wie Polynome und rationale Funktionen zu finden.

Stetigkeit und Ableitung

Satz 1.
Wenn \(f\)differenzierbar im Punkt \(x_0\) ist, dann ist \(f\) stetig im Punkt \(x_0\). Es gilt: \[ \lim_{h\to 0} f(x_0+h) = f(x_0).\]
Ist \(f\)differenzierbar, so folgt \[f(x_0)+h\frac{f(x_0+h)-f(x_0)}{h} \rightarrow f(x_0)+0\cdot f'(x_0)=f(x_0),\] für \(h \to 0\).
Bemerkung. Wenn eine Funktion stetig im Punkt \(x_0\) ist, muss sie nicht in dem Punkt differenzierbar sein. Zum Beispiel ist die Funktion \(g(x) = |x|\) stetig, aber nicht differenzierbar im Punkt \(0\). Dies wurde im vorherigen Kapitel im Beispiel ausführlich besprochen. Zur Erinnerung: Man sich leicht vorstellen, wenn man die Ableitung als Steigung der Tangente interpretiert. Im Punkt \(x_0=0\) lassen sich unendlich viele Tangenten anlegen, somit existiert die Steigung der Tangente nicht.
Ableitungsregeln
Die Ableitung einer Funktion ist über den Grenzwert definiert. Dies ist jedoch für das Bestimmen von Ableitungen sehr umständlich. Als nächstes folgen einige wichtige Regeln, die oft für praktische Probleme bei der Bestimmung der Ableitung einer gegebenen Funktion angewandt werden.Im Folgenden seien \(f\) und \(g\) zwei auf \( \mathbb{R}\) definierte auf \( \mathbb{R}\) differenzierbare Funktionen. Betrachtet man Funktionen, die nur auf offenen Intervallen z.B. \(I_1\) und \(I_2\) differenzierbar sind, dann gelten die folgenden Regeln für ein offenes Intervall \(I \in I_1 \cap I_2 \).

Ein konstanter Faktor
Ist \( f \) eine Funktion der Form \[ f(x) = k \cdot u(x) \] mit der reellen Zahl \( k \) und der Funktion \( u \), dann gilt: \[ f'(x) = k \cdot u'(x) \]

Die Summenregel
\[(f+g)'(x) = f'(x) + g'(x)\]

Die Produktregel
\[(fg)'(x) = f'(x)g(x) + f(x)g'(x)\]

Die Ableitungsregel für Polynome
\[ (ax^m)' = amx^{m-1} \text{, } m \in \mathbb{Z}\]

Die Umkehrfunktion (Reziproke Regel)
\[\Big(\frac{1}{f}\Big)'(x) = - \frac{f'(x)}{f(x)^2} \text{, } f(x) \neq 0\]

Die Quotientenregel
\[(f/g)'(x) = \frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2},\ g(x) \neq 0\]
Beispiel 1:
\[\begin{aligned}\frac{d}{dx}(x^{2006}+5x^3+42) &= \frac{d}{dx}x^{2006}+5\cdot \frac{d}{dx}x^3+42\cdot \frac{d}{dx}1 \\ &= 2006x^{2005}+5\cdot 3x^2+42\cdot 0 \\ &= 2006x^{2005}+5\cdot 3x^2+0 \\ &= 2006x^{2005}+5\cdot 3x^2 \\ &= 2006x^{2005}+15x^2 \end{aligned}\]
Beispiel 2:
\[\begin{aligned}\frac{d}{dx} [(x^4-2)(2x+1)] &= \frac{d}{dx}(x^4-2) \cdot (2x+1) + (x^4-2) \cdot \frac{d}{dx}(2x + 1) \\ &= 4x^3(2x+1) + 2(x^4-2) \\ &= 8x^4+4x^3+2x^4-4 \\ &= 10x^4+4x^3-4.\end{aligned}\]
Bemerkung. Wir können die Antwort überprüfen, indem wir auf eine andere Weise ableiten: \[\frac{d}{dx} [(x^4-2)(2x+1)] = \frac{d}{dx} (2x^5 +x^4 -4x -2) = 10x^4 +4x^3 -4.\]
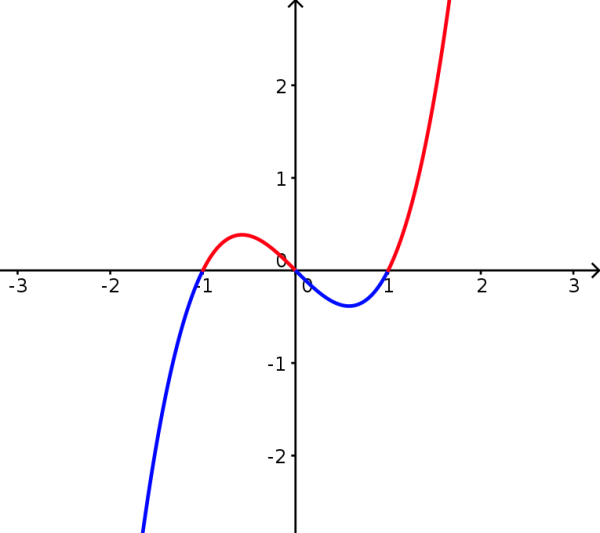
Die Funktion \( (x^4-2)(2x+1) \).
Beispiel 3:
Für \(x \neq 0\) erhalten wir \[\frac{d}{dx} \frac{3}{x^3} = 3 \cdot \frac{d}{dx} \frac{1}{x^3} = -3 \cdot \frac{\frac{d}{dx} x^3}{(x^3)^2} = -3 \cdot \frac{3x^2}{x^6}= - \frac{9}{x^4}.\]
Bemerkung. Es gibt einen weiteren Weg, um die obige Aufgabe zu lösen, indem man bemerkt, dass \(\frac{1}{x^3} = x^{-3}\) ist und mit der Regel für Exponenten ableitet: \[\frac{d}{dx} \ \frac{3}{x^3} = 3 \cdot \frac{d}{dx} x^{-3} = 3 \cdot (-3x^{-4})= - \frac{9}{x^4}\]
Beispiel 4:
\[\begin{aligned}\frac{d}{dx} \frac{x^3}{1+x^2} & = \frac{(\frac{d}{dx}x^3)(1+x^2)-x^3\frac{d}{dx}(1+x^2)}{(1+x^2)^2} \\ & = \frac{3x^2(1+x^2)-x^3(2x)}{(1+x^2)^2} \\ & = \frac{3x^2+x^4}{(1+x^2)^2}.\end{aligned}\]
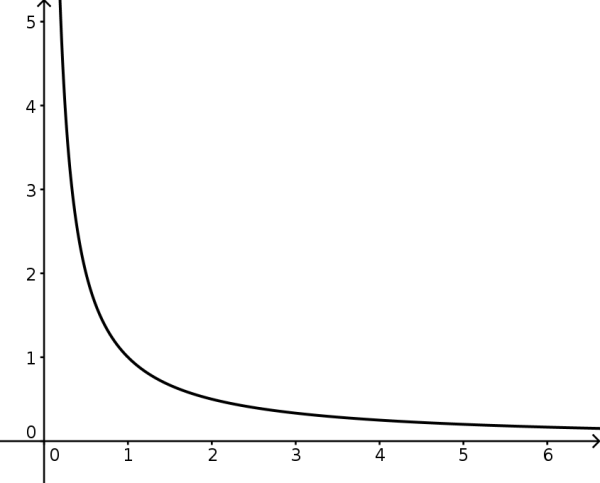
Die Funktion \(\frac{x^3}{1+x^2}\).
Satz von Rolle

Version I
Seien \(a<b\) und \( f: [a,b]\to \mathbb {R} \) eine stetige Funktion, die im offenen Intervall \((a,b)\) differenzierbar ist. Und es gelte \(f(a)=f(b)\). Dann existiert ein \(x_0 \in (a,b) mit f'(x_0)=0\).
Version II
Seien \(a<b\) und \( f: [a,b]\to \mathbb {R} \) eine stetige Funktion, die im offenen Intervall \((a,b)\) differenzierbar ist. Wenn \(f\) differenzierbar im lokalen Extremum \(x_0\in \, (a,b)\) ist, dann gilt \(f'(x_0)=0\).
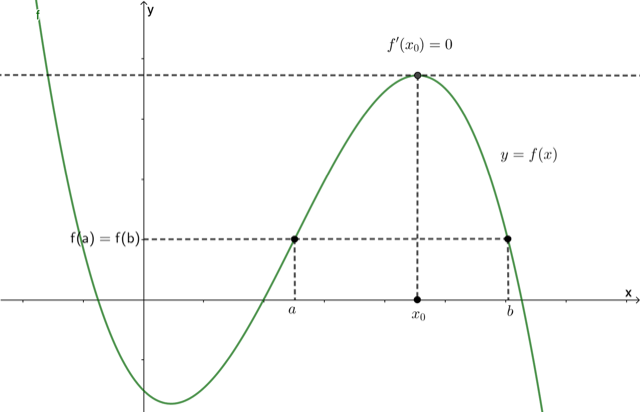
Visualisierung Satz von Rolle
Die L'Hospitalschen Regeln
Ein nützlicher Satz für die Bestimmung von Grenzwerten ist der Satz von L'Hospitalschen. Es gibt viele verschiedene Varianten dieser Regel, aber wir stellen eine einfache Form vor.
Wir nehmen dafür an, dass \(f(x_0)=g(x_0)=0\) gilt und die Funktionen\(f,g\)differenzierbar auf einem Intervall \((x_0-\delta,x_0+\delta)\) sind.

Wenn \[ \lim_{x\to x_0}\frac{f'(x)}{g'(x)} \] existiert, dann gilt \[ \lim_{x\to x_0}\frac{f(x)}{g(x)}=\lim_{x\to x_0}\frac{f'(x)}{g'(x)}. \]

Wir betrachten \[ \lim_{x\to 0}\frac{sin(x)}{x} \]. Es gilt also \[ \lim_{x\to 0}\frac{sin(x)}{x} = \frac{sin(0)}{0} = \frac{0}{0} \] Hier kann man den Limes hier nicht direkt ausrechnen. Hier wendet man also die L'Hospitalschen Regeln an. Man betrachtet nun die Funktionen \[ f(x) = sin(x) \] und \[ g(x) = x \] Diese werden getrennt voneinander abgeleitet. Es ergeben sich folgende Ableitungen: \[ f'(x) = cos(x) \] und \[ g'(x) = 1 \]. Als nächstes bestimmt man \[ \lim_{x\to 0}\frac{f'(x)}{g'(x)} = \lim_{x\to 0}\frac{cos(x)}{1} = \frac{cos(0)}{1} = 1 \]. Somit ist der Grenzwert \[ \lim_{x\to 0}\frac{f(x)}{g(x)} = \lim_{x\to 0}\frac{sin(x)}{x} = \lim_{x\to 0}\frac{f'(x)}{g'(x)} = \lim_{x\to 0}\frac{cos(x)}{1} = 1 \]

5.3. Spezielle Ableitungen

In diesem Kapitel beschäftigen wir uns mit speziellen Ableitungen:
- Trigonometrische Funktionen
- verknüpfte Funktionen
- Exponential- und Logarithmusfunktion
Trigonometrische Funktionen
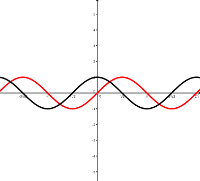
Die Funktion \(\color{red}\sin\color{red}(\color{red}x\color{red})\) und ihre Ableitungs-Funktion \(\cos(x)\).
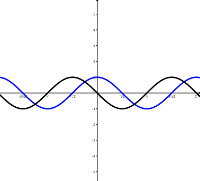
Die Funktion \(\color{blue}\cos\color{blue}(\color{blue}x\color{blue})\) und ihre Ableitungs-Funktion \(-\sin(x)\).
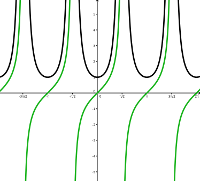
Die Funktion \(\color{green}\tan\color{green}(\color{green}x\color{green})\) und ihre Ableitungsfunktion \(1/\cos^2(x)\).
Beispiel 1:
\[\frac{d}{dx} (3 \sin(x)) = 3 \sin'(x) = 3 \cos(x).\]
Beispiel 2:
\[\frac{d}{dx} \cos^2 (x) = \cos'(x) \cdot \cos(x) + \cos(x) \cdot \cos'(x) = -2\sin(x)\cos(x).\]
Beispiel 3:
\[\begin{aligned} \frac{d}{dx} \frac{\sin(x) + 1}{\cos(x)} &= \frac{d}{dx} \left( \frac{\sin(x)}{\cos(x)} + \frac{1}{\cos(x)} \right) \\ &= \tan'(x) - \frac{\cos'(x)}{\cos^2(x)} \\ &= \frac{1+\sin(x)}{\cos^2 (x)}.\end{aligned}\]
Kettenregel
In diesem Abschnitt lernen wir die Formel zur Bestimmung der Ableitung einer Komposition von Funktionen kennen. Diese wichtige Regel ist bekannt als Kettenregel, damit lassen sich Funktionen wie z.B. \(sin(2x)\) ableiten.
Sei \(f\colon \mathbb{R}\to \mathbb{R}\), \(g\colon \mathbb{R}\to \mathbb{R}\) und \(f \circ g \colon \mathbb{R}\to \mathbb{R}\).

Die Kettenregel.
Sei \(g\) differenzierbar im Punkt \(x\) und \(f\) differenzierbar in \(g(x)\). Dann gilt \[\frac{d}{dx}f(g(x))=f'(g(x))g'(x).\]

Beispiel 1:
Es ist die Funktion \((2x-1)^3\) zu differenzieren. Wir nehmen \(f(x) = x^3\) und \(g(x) = 2x-1\) und differenzieren die Komposition \(f(g(x))\). Da \[f'(x) = 3x^2 \text{ and } g'(x) = 2,\] erhalten wir \[\frac{d}{dx} (2x-1)^3 = 3(2x-1)^2 \cdot 2 = 6(4x^2-4x+1) = 24x^2-24x+6.\]
Die Funktion \(\color{green}(\color{green}2\color{green}x\color{green}-\color{green}1\color{green})^\color{green}3\) und und ihre Ableitungsfunktion.
Beispiel 2:
Wir müssen die Funktion \(\sin 3x\) differenzieren. Nehme \(f(x) = \sin x\) und \(g(x) = 3x\), dann differenziere die Komposition \(f(g(x))\). \[\frac{d}{dx} \sin 3x = \cos 3x \cdot 3 = 3 \cos 3x.\]
Bemerkung. Sei \(h\colon \mathbb{R}\to \mathbb{R}, g\colon \mathbb{R}\to \mathbb{R}\) und \(f\colon \mathbb{R}\to \mathbb{R}\). Nun folgt \[\frac{d}{dx}f(g(h(x)))=f'(g(h(x)))\frac{d}{dx}g(h(x))=f'(g(h(x)))g'(h(x))h'(x).\] Auf ähnliche Weise erhält man komplexere Regeln für Kompositionen von mehreren Funktionen.
Beispiel 3:
Differenziere die Funktion \(\cos^3 2x\). Wähle \(f(x) = x^3\), \(g(x) = \cos x\) und \(h(x) = 2x\) und differenziere die Komposition \(f(g(h(x)))\). \[\begin{aligned}\frac{d}{dx} \cos^3 2x &= 3(\cos 2x)^2 \cdot \frac{d}{dx} \cos 2x \\ &= 3 \cos^2 2x \cdot (-\sin 2x) \cdot 2 \\ &= -6 \sin 2x \cos^2 2x.\end{aligned}\]
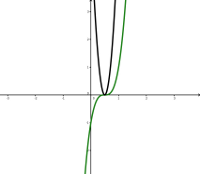
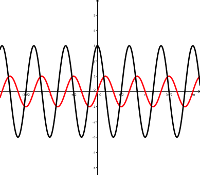 Die Funktion \(\color{red}\sin \color{red}3\color{red}x\) und und ihre Ableitungsfunktion.
Die Funktion \(\color{red}\sin \color{red}3\color{red}x\) und und ihre Ableitungsfunktion. 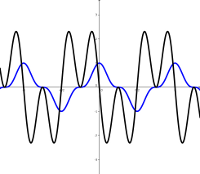
Die Funktion \(\color{blue}\cos^\color{blue}3 \color{blue}2\color{blue}x\) und und ihre Ableitungsfunktion.
Exponential- und Logarithmusfunktion
Wir definieren zwei wichtige Funktionen, die Exponentialfunktion und die Logarithmusfunktion.

Die Exponentialfunktion
Beispiel 1:
Zum Zeitpunkt \(t_0\) ist die Größe einer Bakterien-Kolonie 500. Die Bakterien teilen sich jede halbe Stunde in zwei. Dies bedeutet, dass sich in einer Stunde die Population vervierfacht:
| nach 1 Stunde | \(4 \cdot 500\) |
|---|---|
| nach 2 Stunden | \(4 \cdot (4 \cdot 500) = 4^2 \cdot 500\) |
| nach 3 Stunden | \(4 \cdot (4^2 \cdot 500) = 4^3 \cdot 500\) |
| \(\vdots\) | \(\vdots\) |
| nach t Stunden | \(4^t \cdot 500\) |
Die Funktion, die die Größe der Bakterien Bevölkerung zum Zeitpunkt \(t\) angibt, ist \(f(t) = 500 \cdot 4^t\).
Modellierung des Bevölkerungs-Wachstums
Zum Zeitpunkt \(t\in \mathbb{R}\) ist die Größe der Bevölkerung \(s(t)\), wobei die Wachstums-Geschwindigkeit direkt proportional ist: \(s'(t)=s(t)\). Sei erst \(s(0)=1\). Nun müssen wir eine Lösung für das Anfangswertproblem finden \[\begin{cases}s'=s, \\ s(0)=1.\end{cases}\]
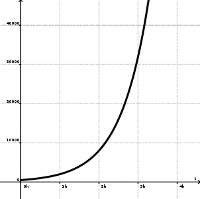
Die Funktion \(500 \cdot 4^t\).

Definition 1 (Exponentialfunktion)
\[\exp(t):=\sum_{k=0}^{\infty} \frac{t^k}{k!}.\]
Die Motivation für diese Definition ist die formale Rechnung \[ \frac{d}{dt}(1+t+\frac{1}{2!}t^2+\frac{1}{3!}t^3+\dots ) = 1+t+\frac{1}{2!}t^2+\frac{1}{3!}t^3+\dots,\] wobei wir die Umformung \( \frac{k}{k!} = \frac{1}{(k-1)!}\) nutzen.
Man kann zeigen, dass die Reihe konvergiert für alle \( t\in\mathbb{R}\) und die Funktion exp die notwendigen Eigenschaften besitzt. Die Beweise sind eher technisch und werden hier weggelassen.
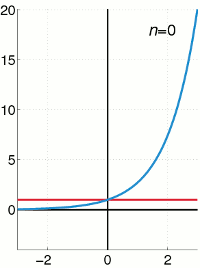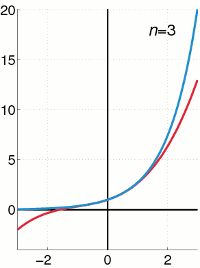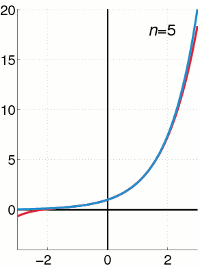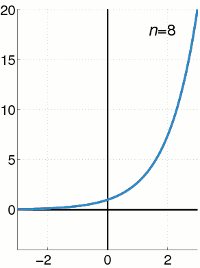
Die Funktion \(e^t\) und die Summe der ersten \(n+1\) Terme von \(\sum_{k=0}^{\infty} \frac{t^k}{k!}.\)

Satz 1.
Für alle \(t\in \mathbb{R}\) haben wir \( \exp (t) = e^t \), mit \( e=\exp(1)\) als sogenannte Napiers Konstante oder Eulersche Zahl.

Satz 2.
\[\frac{d}{dx}\exp(x)=\exp(x).\]
Interaktivität. Die Ableitung der Exponentialfunktion (Der Punkt \( x \) ist waggrecht verschiebbar).

Der natürliche Logarithmus
Anhand der Formel \( \exp (x)=e^x\) sehen wir, dass \(\exp \colon \mathbb{R} \to (0,\infty)\) eine strikt steigende (somit bijektive) Funktion ist. Ihre Inverse heißt natürlicher Logarithmus:
Definition 2
\[\ln:=\exp^{-1}\colon (0,\infty)\to \mathbb{R}.\]
Beispiel 3.
Aus der Definiton erhalten wir \(\exp(\ln(x)) = x\), für \(x>0\). Also \[\begin{aligned}\frac{d}{dx} \exp(\ln(x)) &= \frac{d}{dx}x \\ \exp(\ln(x)) \cdot \frac{d}{dx} \ln(x) &= 1 \\ x \cdot \frac{d}{dx} \ln(x) &= 1 \\ \frac{d}{dx} \ln(x) &= \frac{1}{x} \text{, für } x>0.\end{aligned}\]
Somit haben wir gezeigt:
Natürliche Logarithmus-Funktion \(\ln(x)\).

Satz 3.
\[\frac{d}{dx} \ln(x) = \frac{1}{x}, \text{ wenn } x>0.\]
Interaktivität. Die Ableitung der Logarithmusfunktion.

Exponentialfunktion mit Basis \( a > 0\)
Beispiel 4.
Per Definition \(a^x = \exp(x \ln(a))\). Somit \[\begin{aligned}\frac{d}{dx} a^x &= \frac{d}{dx} \exp(x \ln(a)) \\ &= \exp(x \ln(a)) \cdot \frac{d}{dx} (x \ln(a)) \\ &= a^x \ln(a) \text{, für } a > 0.\end{aligned}\] Somit haben wir bewiesen:
Satz 4.
\[\frac{d}{dx} a^x = a^x \ln(a) \text{, wenn } a > 0\]

Logarithmus mit Basis \(a > 0\)
Die Funktion \((t\mapsto a^t)\colon \mathbb{R} \to (0,\infty)\) ist
-
strikt monoton fallend für \(0 \lt a \lt 1\), und
-
strikt monoton steigend für \(1 \lt a \lt \infty\).
Dann heißt die Inverse Logarithmus mit der Basis \(a\):

Definition 3
\[\log_a \colon (0, \infty) \to \mathbb{R}\]

Satz 5.
Für \(x>0\) \[\frac{d}{dx} \log_a(x) = \frac{1}{x \ln(a)}.\]
Der Logarithmus hat die folgenden Eigenschaften (sofern der jeweilige Logarithmus definiert ist):
Satz 6.
-
\(\log_a(1) = 0\)
-
\(\log_a(a) = 1\)
-
\(\log_a(x^r) = r \log_a(x)\)
-
\(\log_a(a^x) = x\)
-
\(\log_a(x) = \frac{\log_b(x)}{\log_b(a)}\)
-
\(\log_a(xy) = \log_a(x)+\log_a(y)\)
-
\(\log_a(\frac{x}{y}) = \log_a(x)-\log_a(y)\)

5.4. Extremwerte

Extremwerte
Wir werden den Zwischenwertsatz für differenzierbare Funktionen und seine Verbindung zu Extremwert-Problemen behandeln. Wiederholung:

Definition 1.
Eine Funktion \(f\colon A\to \mathbb{R}\) hat ein lokales Maximum im Punkt \(x_0\in A\), wenn für ein \(h\gt 0\) und für alle \(x\in A\) mit \(|x-x_0|\lt h\), gilt \(f(x)\leq f(x_0)\).
Analog hat eine Funktion \(f\colon A\to \mathbb{R}\) ein lokales Minimum im Punkt \(x_0\in A\) , wenn für ein \(h>0\) und für alle \(x\in A\) mit \(|x-x_0|\lt h\), gilt \(f(x)\geq f(x_0)\).
Ein lokales Extremum ist ein lokales Maximum oder ein lokales Minimum.
Um das später für mehrdimensionale Funktionen erweitern zu können, stellen wir noch eine äquivalente Definition vor. Betrachtet man eine Umgebung auf ganz \( \mathbb{R}\) entspricht dies einem Intervall.

Ein Funktionswert \(f(x_0)\) wird als lokales Maximum von \(f\) bezeichnet, wenn eine Umgebung \(U(x_0) \subset D\) existiert, sodass für alle Werte \(x\in U(x_0)\) gilt: \[f(x) \leq f(x_0)\]
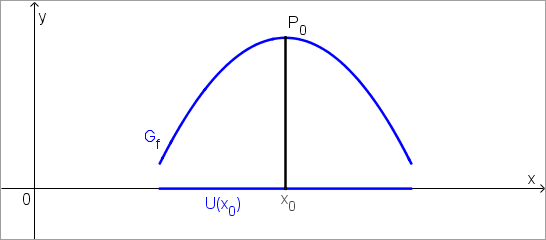

Ein Funktionswert \(f(x_0)\) wird als lokales Minimum von \(f\) bezeichnet, wenn eine Umgebung \(U(x_0) \subset D\) existiert, sodass für alle Werte \(x\in U(x_0)\) gilt: \[f(x) \geq f(x_0)\]
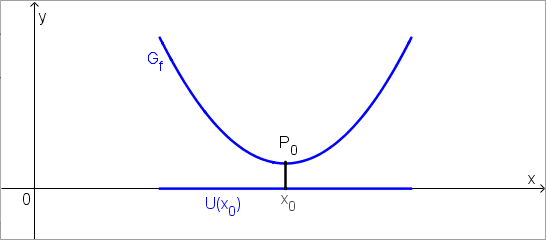

Vorsicht! Bei einem Extremum kann es sich gleichzeitig sowohl um ein Maximum als auch um ein Minimum handeln. S. Bsp. (s. Graphik).
Liegt an einer Stelle \(x_0\) ein Minimum vor, so ist die Funktion für \(x \leq x_0\) in einem (kleinen) Bereich monoton fallend und für \(x \geq x_0\) monoton wachsend. Liegt ein Maximum vor, so kehren sich die Ungleichheitszeichen um.
Hier ist zu beachten, dass dieses Monotonieverhalten lokal zu sehen ist. Eine Funktion kann beliebig viele Extrema aufweisen (z.B. die Sinusfunktion), sodass dieses Kriterium nur in einer gewissen Umgebung von \(x_0\) gilt.
Im Extrempunkt \((x_0 | f(x_0))\) einer Funktion \(f\), also in dem Punkt, in dem sich die Steigung \(f'\) gerade „umkehrt“, verläuft der Graph der Funktion waagrecht. Sie hat eine waagrechte Tangente, bzw. die Steigung \(f'(x_0)=0\). Dies führt zum folgenden Kriterium:
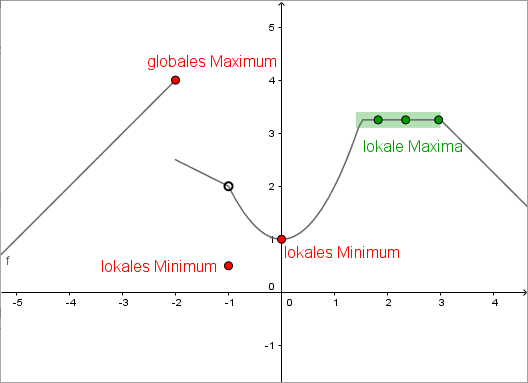
„Typen“ lokaler Extrema
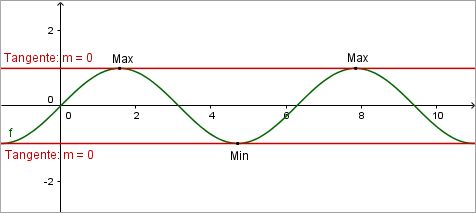
Beispiel Sinusfunktion
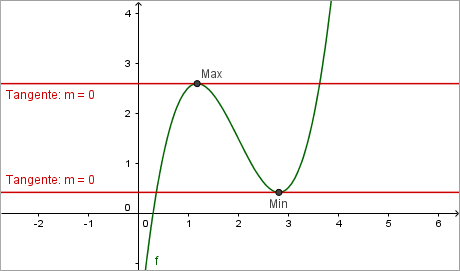
Beispiel waagrechte Tangente

Notwendiges Kriterium für lokale Extremstellen
Satz 1.
Sei \(x_0\in [a,b]\) ein lokaler Extremwert einer stetigen Funktion \(f\colon [a,b]\to \mathbb{R}\). Dann gilt entweder,
-
dass die Ableitung \(f'(x_0)\) nicht existiert (dies beinhaltet auch die Fälle der Randpunkte \(x_0=a\) und \(x_0=b\)) oder
-
\(f'(x_0)=0\).
Beispiel 1
Sei \(f: \mathbb{R} \to \mathbb{R}\) definiert als \[f(x) = x^3 -3x + 1.\] Dann \[f'(x) = 3x^2-3\] und wir sehen, dass wir für \(x_0 = -1\) und \(x_1 = 1\) Kandidaten für lokale Maxima und Minima von \(f\) erhalten, denn
\[f'(-1) = 3 \cdot (-1)^2 - 3 = 0 \text{ und } f'(1) = 3 \cdot 1^2 - 3 = 0.\]
Anhand des blauen Graphen rechts können wir sehen, dass \(x_0\) das lokale Maximum und \( x_1 \) das lokale Minimum der Funktion darstellt.
ACHTUNG: Die Eigenschaft eine Nullstelle der Ableitung zu sein ist nur ein notwendiges, aber kein hinreichendes Kriterium für Extremstellen. Das heißt jedes lokale Extremum (einer differenzierbaren Funktion) hat als Ableitung den Wert 0, aber nicht jede Nullstelle der Ableitungsfunktion ist ein lokales Extremum. Solche Punkte nennt man Sattelpunkte. Dazu ein Beispiel:
Sei \(f: \mathbb{R} \to \mathbb{R}\) definiert als \[f(x) = x^3.\]
Zunächst ist \( f'(x) = 3x^2 \) und als einzige Nullstelle von \( f' \) erhält man \( x_0 = 0 \). Jedoch ist dies weder ein lokales Minimum noch Maximum wie der Graph zeigt. D.h. anhand geeigneter Methoden, die wir kennenlernen werden, muss dies zusätzlich gezeigt werden. Anhand derer kann dann aber entschieden werden, ob ein Minimum oder Maximum vorliegt.
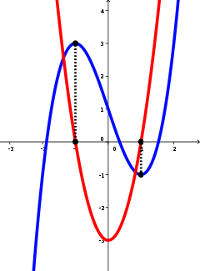
Die Funktion \(x^3-3x+1\) und ihre Ableitungsfunktion \(3x^2-3\).
Hinreichende Kriterien für lokale Extremstellen
\(f\) sei eine auf einem offenen Intervall \(I\) differenzierbare Funktion und \(x_0 \in I\).
1. hinreichendes Kriterium:
Ist \(x_0\) eine Nullstelle von \(f'\) und hat \(f‘\) in \(x_0\) einen Vorzeichenwechsel, so ist \(x_0\) eine lokale Extremstelle von \(f\).
2. hinreichendes Kriterium:
Gilt \(f'(x_0) = 0\) und \(f''(x_0) \neq 0\), so ist \(x_0\) lokale Extremstelle von \(f\).
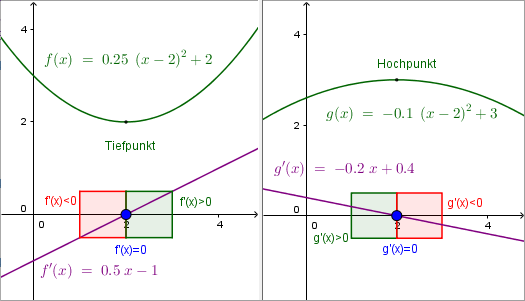
VZW Vorzeichenwechsel:
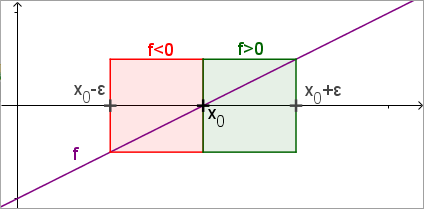
D. h., es existiert \(\epsilon > 0\), sodass auf \((x_0-\epsilon, x_0)\) gilt: \(f'(x)<0\) und auf \((x_0, x_0+ \epsilon)\) gilt: \(f'(x)>0\); oder das Gleiche mit vertauschen Relationszeichnen.
Im Anschluss an die Überprüfung dieser Kriterien bleibt der Funktionswert \(f(x_0)\) an der Stelle \(x_0\) zu berechnen.
Außerdem bleibt zu klären, ob es sich bei dem so gefundenen Extremum um ein Maximum oder ein Minimum handelt.
- Je nach Verlauf des Vorzeichenwechsels liegt ein Minimum (VZW von „Minus“ zu „Plus“) oder ein Maximum (VZW von „Plus“ zu „Minus“) vor. Dies ist gleichbedeutend damit, dass die Ableitung \(f'\) zuerst fällt und dann steigt, bzw. umgekehrt.
- Ist die zweite Ableitung \(f''(x_0)\) positiv (dies entspricht einem VZW von „Minus“ zu „Plus“, so liegt ein Minimum vor; ist \(f''(x_0)\) negativ, so liegt ein Maximum vor.
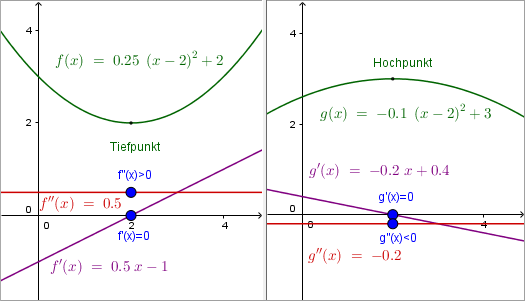
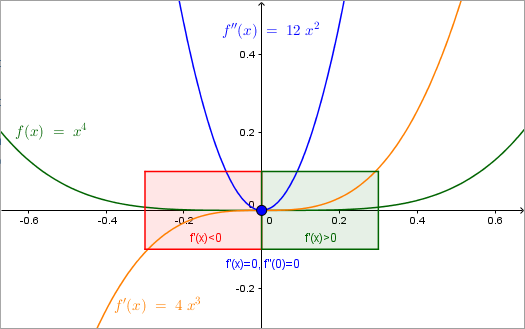
Ermitteln der globalen Extrema
In der Praxis, wenn wir die lokalen Extrema einer gegebenen Funktion suchen, müssen wir drei Punkte überprüfen:
-
Die Nullstellen der Ableitung
-
Die Randpunkte des Definitionsbereiches (Intervall)
-
Punkte, an denen die Funktion nicht differenzierbar ist.
Falls wir bereits vorher wissen, dass die Funktion ein Maximum/Minimum besitzt, dann beginnen wir damit alle möglichen lokalen Extrema ausfindig zu machen (nach den obigen Punkten), die Funktion an diesen auszuwerten und den größten/kleinsten Wert zu wählen.
Beispiel 2
Zu finden ist der kleinste und der größte Wert der Funktion \(f\colon [0,2]\to \mathbf{R}\), \(f(x)=x^3-6x\). Da die Funktion stetig auf einem geschlossenen Intervall ist, besitzt sie ein Maximum und ein Minimum. Da die Funktion differenzierbar ist, genügt es die Randpunkte des Intervalls und die Nullstellen der Ableitung innerhalb des Intervalls zu untersuchen.
Die Nullstellen der Ableitung: \(f'(x)=3x^2-6=0 \Leftrightarrow x=\pm \sqrt{2}\). Da \(-\sqrt{2}\not\in [0,2]\), brauchen wir die Funktion nur an drei Punkten auszuwerten, \(f(0)=0\), \(f(\sqrt{2})=-4\sqrt{2}\) und \(f(2)=-4\). An diesen können wir sehen, dass der kleinste Wert der Funktion \(-4\sqrt{2}\) und der größte Wert \(0\) dementsprechend ist..
Als nächstes formulieren wir ein fundamentales Ergebnis für differenzierbare Funktionen. Die grundlegende Idee hier ist, dass eine Änderung auf dem Intervall nur geschehen kann, wenn auch eine Änderung im Intervall stattfindet.

Satz 2 (Mittelwertsatz)
Sei \(f\colon [a,b]\to \mathbb{R}\) stetig auf dem Intervall \([a,b]\) und differenzierbar im Intervall \((a,b)\). Dann gilt \[f'(x_0)=\frac{f(b)-f(a)}{b-a}\] für ein \(x_0\in (a,b).\)

Zunächst wollen wir betrachten, was der Mittelwertsatz (MWS) aussagt; hierfür betrachten wir uns die Gleichung genauer: Auf der rechten Seite steht letztlich nichts anderes als die Sekantensteigung zwischen den Punkten \( (a, f(a)) \) und \( (b, f(b)) \). Der MWS besagt nun, dass es mindestens eine Stelle \( x_0 \) im Intervall \( (a,b) \) gibt, sodass dort die Tangentensteigung \( f'(x_0) \) damit identisch ist.
Geometrisch können wir also die Sekante zwischen den Punkten \( (a, f(a)) \) und \( (b, f(b)) \) parallel so verschieben, dass sie zu einer Tangente im Punkt \( (x_0,f(x_0)) \) wird.
Mit Hilfe des MWS können wir nun folgendes wichtiges Resultat für die Anwendung beweisen. Dabei nutzen wir aus, dass die Gleichung des MWS im Grenzfall von der Sekanten- zur Tangentensteigung wird und damit die Ableitung in einem Punkt repräsentiert.

Satz 3
Sei \(f\colon (a,b)\to \mathbb{R}\) eine differenzierbare Funktion. Dann gilt:
-
Genau dann wenn für alle \(x\in (a,b) \ \ f'(x)\geq 0\) gilt, dann ist \(f\) steigend,
-
Genau dann wenn für alle \(x\in (a,b) \ \ f'(x)\leq 0\) gilt, dann ist \(f\) fallend.

Hinweis: Man kann auch eine etwas stärkere Aussage mit einer sehr ähnliche Beweisidee zeigen. Diese gilt allerdings nur in eine Richtung, d.h. man kann nur aus den Werten der Ableitung auf die Monotonie schließen und nicht umgekehrt.
Wenn für alle \(x\in (a,b) \ \ f'(x) > 0\) gilt, dann ist \(f\) streng monoton steigend bzw. wenn für alle \(x\in (a,b) \ \ f'(x) < 0\) gilt, dann ist \(f\) streng monoton fallend.
Ein Beispiel, dass die Rückrichtung im Allgemeinen nicht gilt, ist \(f(x) = x^3\). Die Funktion \( f \) ist zwar streng monoton steigend \(( f(x_2) - f(x_1) > 0 \) für alle \( x_2 > x_1 )\), aber es gilt \( f'(0)=0 \).
Beispiel 3
Für das Polynom \(f(x) = \frac{1}{4} x^4-2x^2-7\) ist die Ableitung \[f'(x) = x^3-4x = x(x^2-4) = 0,\] wenn \(x=0\), \(x=2\) oder \(x=-2\). Nun können wir eine Tabelle anlegen und mithilfe derer entscheiden, ob ein Minimum oder Maximum vorliegt:
| \(x<-2\) | \(-2 \lt x \lt 0\) | \(0 \lt x \lt 2\) | \(x>2\) | |
|---|---|---|---|---|
| \(x\) | \(<0\) | \(<0\) | \(>0\) | \(>0\) |
| \(x^2-4\) | \(>0\) | \(<0\) | \(<0\) | \(>0\) |
| \(f'(x)\) | \(<0\) | \(>0\) | \(<0\) | \(>0\) |
| \(f(x)\) | fallend | steigend | fallend | steigend |
Beispiel 4
Gesucht ist ein Rechteck, so dass der Flächeninhalt \(9\) beträgt und der Umfang möglichst klein ist.
Seien \(x\ (>0)\) und \(y\ (>0)\) die Seiten des Rechtecks. Dann gilt \(x \cdot y = 9\) und wir erhalten \(y=\frac{9}{x}\). Der Umfang lässt sich schreiben als \[2x+2y = 2x+2 \frac{9}{x} = \frac{2x^2+18}{x}.\] In welchem Punkt nimmt die Funktion \(f(x) = \frac{2x^2+18}{x}\) ihren kleinsten Wert an? Die Funktion \(f\) ist stetig und differenzierbar für \(x>0\) und durch Anwendung der Quotientenregel erhalten wir \[f'(x) = \frac{4x \cdot x-(2x^2+18) \cdot 1}{x^2} = \frac{2x^2-18}{x^2}.\] Nun ist \(f'(x) = 0\), wenn \[\begin{aligned}2x^2-18 &= 0 \\ 2x^2 &= 18 \\ x^2 &= 9 \\ x &= \pm 3\end{aligned}\] aber wir haben \(x>0\) voraussgesetzt, also interessiert uns nur der Fall \(x=3\). Hierzu legen wir eine Tabelle an:
| \(x<3\) | \(x>3\) | |
|---|---|---|
| \(f'(x)\) | \(<0\) | \(>0\) |
| \(f(x)\) | fallend | steigend |
Da die Funktion \(f\) stetig ist, wissen wir nun, dass sie ihr Minimum im Punkt \(x=3\). Jetzt können wir die andere Seite des Rechtecks berechnen: \(y=\frac{9}{x}=\frac{9}{3}=3\).
Somit ist das Rechteck mit dem geringsten Umfang in Wirklichkeit ein Quadrat mit der Seitenlänge \(3\).
Die Funktion \(\frac{1}{4} x^4-2x^2-7\).
Die Funktion \(\frac{2x^2+18}{x}\).
Beispiel 5
Wir bestimmen einen 1-Liter Meßbecher, welcher die Form eines Zylinders mit der Grundfläche eines Kreises hat ohne einen Deckel. Gesucht ist die optimale Größe für den Boden und die Höhe, so dass die geringste Menge an Material für den Meßbecher benötigt wird.
Sei \(r > 0\) der Radius und \(h > 0\) die Höhe des Zylinders. Das Volumen des Zylinder ist \(1\) dm\(^3\) und wir können \(\pi r^2 h = 1\) umschreiben und erhalten \[h = \frac{1}{\pi r^2}.\]
Die benötigte Materialmenge entspricht dem Oberflächeninhalt \[A_{\text{bottom}} + A_{\text{side}} = \pi r^2 + 2 \pi r h = \pi r^2 + \frac{2 \pi r}{\pi r^2} = \pi r^2 + \frac{2}{r}.\]
Sei die Funktion \(f: (0, \infty) \to \mathbb{R}\) definiert als \[f(r) = \pi r^2 + \frac{2}{r}.\] Wir müssen den Wert für das Minimum der Funktion \(f\), die stetig und differenzierbar ist, finden für \(r>0\). Anwenden der Ableitungsregel für Umkehrfunktionen liefert \[f'(r) = 2\pi r -2 \cdot \frac{1}{r^2} = \frac{2\pi r^3 - 2}{r^2}.\] Nun ist \(f'(r) = 0\), wenn \[\begin{aligned}2\pi r^3 - 2 &= 0 \\ 2\pi r^3 &= 2 \\ r^3 &= \frac{1}{\pi} \\ r &= \frac{1}{\sqrt[3]{\pi}}.\end{aligned}\]
Lege hierzu eine Tabelle an:
| \(r<\frac{1}{\sqrt[3]{\pi}}\) | \(r>\frac{1}{\sqrt[3]{\pi}}\) | |
|---|---|---|
| \(f'(r)\) | \(<0\) | \(>0\) |
| \(f(r)\) | fallend | steigend |
Da die Funktion \(f\) stetig ist, wissen wir, dass sie ihr Minimum für den Wert \(r= \frac{1}{\sqrt[3]{\pi}} \approx 0.683\) annimmt. Dann \[h = \frac{1}{\pi r^2} = \frac{1}{\pi \left(\frac{1}{\sqrt[3]{\pi}}\right)^2} = \frac{1}{\frac{\pi}{\pi^{2/3}}} = \frac{1}{\sqrt[3]{\pi}} \approx 0.683.\]
Das heißt, die geringste Menge an Material für den Meßbecher beträgt ungefähr \(2 \cdot 0.683\) dm \( = 1.366\) dm \( \approx 13.7\) cm im Durchmesser und ist \(0.683\) dm \( \approx 6.8\) cm hoch.
Die Funktion \(\pi r^2 + \frac{2}{r}\).

5.5. Exkurs: Anwendungsbeispiel


In unserer von Wirtschaftlichkeit und Effizienz geprägten Welt sind Optimierungen überall zu finden: Prozessoptimierungen in der Fertigung, Optimierung von Lieferungen im Bereich der Logistik, Optimierung der Auslastung von Arbeitskräften, Verbesserungen der Flächenausnutzung etc. Viele Beispiele sind für den normalen Schulunterricht zu komplex oder haben einen zu großen Zeitbedarf, so dass sie primär an Projekttagen oder in Projektwochen angegangen werden können.
Ein traditionsreiches Beispiel aus dem Unterricht stellt die Optimierung einer offenen Schachtel hinsichtlich eines möglichst großen Volumens dar, die aus einem DIN-A4-Karton hergestellt werden soll.
Zunächst vereinfachen wir die Situation folgendermaßen: Die Stärke des Kartons und damit zusammenhängende Schwierigkeiten beim Falten vernachlässigen wir. Ebenso betrachten wir nicht die verschiedenen Möglichkeiten, wie die Schachtel stabil verklebt werden soll. Uns geht es erst einmal nur um das Volumen.
Der Karton ist zunächst rechteckig. Durch das Abschneiden quadratischer Stücke der Seitenlänge h an den Ecken erhalten wir das Netz einer offenen, quaderförmigen Schachtel.
Für das Volumen dieser Schachtel stellen wir folgende Formel auf:
Seitenlängen des Kartons: \(a\), \(b\)
Volumen der offenen Schachtel: \( V(h)=h\cdot (a-2h)\cdot (b-2h)= 4 \cdot h^3 -2 \cdot a \cdot h^2 - 2 \cdot b \cdot h^2 + a\cdot b \cdot h \)
Die Grafik zeigt den Graphen dieser Funktion im relevanten Abschnitt, in dem das Maximum gesucht wird. Variabel sind hier die Werte der Schieberegler für die Seitenlängen a und b (für DIN-A4: a=21; b= 29,7). Außerdem kann die Höhe h dadurch eingestellt werden, dass der mit h bezeichnete Punkt auf der x-Achse bewegt wird. Das Volumen an der Stelle h verändert sich mit der Veränderung der Höhe passend.
Durch Ausprobieren mit Hilfe eines Schiebereglers nähern wir das maximale Volumen bei 678,7 cm³ für eine Höhe von 1,71 cm an. Rechnerisch ergibt sich der Wert über das Bestimmen der Ableitung der Funktion V nach der betrachteten Höhe h (die man im Unterricht natürlich auch x nennen kann) zu 1,75 cm und eine Volumen von 678,74 cm³.
Anstatt experimentell mit GeoGebra nach einem Maximum zu suchen, bietet es sich auch an, mit Hilfe von Ableitungen das Maximum zu bestimmen. Später kann dieses Verfahren auf weitere Optimierungsprobleme angewendet werden, deren Extrema anders kaum zu bestimmen sind.
Für die Volumensfunktion der offenen Schachtel
\[ V(h)=h\cdot (a-2h)\cdot (b-2h)=4 \cdot h^3 -2 \cdot a \cdot h^2 - 2 \cdot b \cdot h^2 + a\cdot b \cdot h \]
erhalten wir als Ableitung: \[ V'(h)=12 h^2 -4ah-4bh+ab \]
Für die Werte eines DIN-A4-Blatts a = 210 und b = 297 (Einheit mm) erhalten wir \[ V(h)=h\cdot (210-2h)\cdot (297-2h)=(-4h)^3-4h^2+(210+297)h+62370 \] bzw. \[ V'(h)=12 h^2 +62370-4\cdot 210 \cdot h-4 \cdot 297\cdot h \] Als Lösungen der Gleichung \[ V'(h) = 0 \] erhalten wir mit einem CAS die Lösungsmenge \[ L = \{40,42; 128,58\} \]
Nur der erste, kleinere Wert ist eine sinnvolle Lösung, da der zweite Wert die Hälfte der kürzeren Seitenlänge eines DIN-A4-Blattes übersteigt.



Für die erste, einfachste Modellierung nehmen wir an, dass der Quader eine quadratische Grundfläche besitzen und einen Liter Volumen fassen soll.
Das Volumen des Körpers berechnet sich so: \( V \ = \ A \cdot h \ = \ b^2 \cdot h \) , wobei A die Grundfläche bzw. b die Breite und h die Höhe der Tüte bezeichnet.
In der Funktion für die Oberfläche sind die Variablen Breite b und Höhe h enthalten. Durch die Nebenbedingung, dass das Volumen 1 Liter betragen soll, ergibt sich der Zusammenhang zwischen Höhe und Breite zu: \( h \ = \ \frac{V}{b^2} \).
Setzen wir dies in die Oberflächenfunktion ein, so erhalten wir eine Funktion, die nur von einer Variablen abhängt.
\( O(b) \ = \ 2\cdot b^2 + 4 \cdot b \cdot \frac{V}{b^2} \ = \ 2 \cdot b^2 + 4 \cdot \frac{V}{b} \)
Ableiten der Funktion ergibt:
\( O'(b) \ = \ 4 \cdot b - 4 \cdot \frac{V}{b^2} \)
Damit können wir die Extremwerte bestimmen:
\( O'(b) \ = \ 4 \cdot b - 4 \cdot \frac{V}{b^2} \ = \ 0 \)
\( b \ = \ \sqrt[3]{V} \)
Für das Volumen von 1000 cm³ ergibt sich eine Breite von:
\( b \ = \ \sqrt[3]{1000 cm^3} \ = \ 10 \ cm \)
Überprüfen wir nun noch, ob es sich tatsächlich um ein Minimum handelt. Dafür muss die zweite Ableitung an der Stelle des Extremwerts positiv sein.
\( O''(b) \ = \ 4 + 8 \cdot \frac{V}{b^3} \)
Da dies für b = 10 cm der Fall ist, handelt es sich hier um ein Minimum. Für die Höhe der Milchtüte ergibt sich \( h \ = \ \frac{1000 \ cm^3}{(10 \ cm)^2} \ = \ 10 \ cm \)
Die nach dieser Modellierung hergestellte Tüte wäre also würfelförmig mit Kantenlänge 10 cm. Die dafür benötigte Materialfläche wäre \( O(10) \ = \ 2 \cdot 10^2 + 4 \cdot \frac{1000}{10} \ = \ 600 \ cm^2 \) .
- Die Oberfläche der Verpackung und damit der Materialverbrauch ist minimal.
- Die Packung ist sehr gut stapelbar.
Welche Gründe sprechen dagegen, dass eine Verpackung so hergestellt wird?
- In der Modellierung wurden keine Klebelaschen berücksichtig. Aus Pappe ließe sich so ein Karton also nur sehr schwer herstellen.
- Bisher haben wir keinerlei Öffnung vorgesehen.
- Ein Würfel mit Kantenlänge 10 cm ist unhandlich und nur schlecht mit einer Hand zu greifen.
- Durch die randvolle Befüllung ist dosiertes Ausschenken schwierig.
- Eine Optimierung des Schnittmusters auf Massenfertigung wurde nicht untersucht.
Fazit: Es ist nicht sinnvoll, nur den Materialverbrauch zu optimieren, da für ein reales Produkt auch andere Faktoren eine Rolle spielen.
Für die zweite Modellierung drehen wir die Richtung einmal um und starten mit der Untersuchung einer echten Giebeldachtüte.
Die Abbildung zeigt das Netz aus Karton, aus dem die Safttüte gefaltet wird, und eine handelsübliche Giebeldachtüte, allerdings mit einem Schraubverschluss für das Ausgießen. In unserer Modellierung werden wir den Schraubverschluss nicht berücksichtigen.
Eine Safttüte ist im Normalfall bis zur Höhe des quaderförmigen Teils der 1-Liter–Safttüte gefüllt. Daher geben wir die Funktion für den Materialverbrauch in Abhängigkeit der Breite a (Seitenlänge der quadratischen Grundfläche) und der Höhe h des quaderförmigen Teils einer Safttüte an.
Im Netz sehen wir in der Mitte vier lange Rechtecke für die Seitenflächen mit Flächeninhalt \( A \ = \ a \cdot h \). Darunter vier kleinere Rechtecke mit Flächeninhalt \( A \ = \ a \cdot \frac{a}{2} \) , die zusammengefaltet den quadratischen Boden der Tüte bilden. Die Rechtecke oben im Netz bilden nach dem Zusammenfalten das Giebeldach. Ihr Flächeninhalt beläuft sich auf \( A \ = \ a \cdot \frac{a}{\sqrt{3}} \). Die restlichen Rechtecke an den unteren, linken und oberen Rändern sind die Klebeflächen mit den originalen Abmessungen.
Neben diesen genutzten Flächen gehört zum Materialverbrauch auch noch die nicht benötigten, ausgestanzten Flächen, die das Netz zu einem großen, aber möglichst kleinen Rechteck ergänzen.
Die Abmessungen für das Giebeldach haben wir einfach angegeben, aber natürlich sind diese nicht a priori klar, sondern müssen bestimmt werden. Dazu betrachten wir die verklebte Tüte von der Seite und bestimmen die nötigen Größen.
Der spitze Basiswinkel des in Grün eingezeichneten, gleichschenkligen Dreiecks beträgt etwa 30°. Daraus ergibt sich:
\( \cos(\alpha) \ = \ \frac{\frac{a}{2}}{L} \ \rightarrow \ L \ = \ \frac{\frac{a}{2}}{\cos(30°)} \ = \ \frac{a}{\sqrt{3}} \)
Das obige Netz für die 1 l – Safttüte wird aus einer Papierrolle ausgestanzt. Aus einer Papierrolle will man möglichst viele Netze und damit Safttüten ausstanzen können. Dies wird erreicht, indem man die Netze aneinander anliegen lässt. Dabei entstehen sowohl zwischen den oberen als auch zwischen den unteren Klebefalzen Stanzabfälle. Diese tragen ebenfalls zum Materialverbrauch bei und müssen bei der Berechnung des Materialverbrauches berücksichtigt werden. Um den Materialverbrauch zu bestimmen, ergänzt man das Netz zu einem Rechteck, welches minimale Fläche besitzt und das Netz komplett umschließt, und berechnet dessen Fläche. Die Abmessungen ergeben sich durch die maximale Länge und Breite des Netzes der 1 l – Safttüte. Man muss also noch die Länge des Klebefalzstreifens oben sowie die Länge der kleinen Klebefalzaufsätze oben und den größten unteren Klebeaufsatz und die Breite des Klebefalzstreifens links am realen Netz abmessen. Die Maße dafür haben wir bereits in das Netz eingetragen.
Der Materialverbrauch - hier als vorläufige Funktion \( \tilde{M} \) bezeichnet - ergibt sich also wie folgt:
\( \tilde{M}(a, h) \ = \ B \cdot L \)
\( \tilde{M}(a, h) \ = \ (1,0 \ \text{cm} \ + \ 4 \cdot a)\cdot (1,4 \ \text{cm} \ + \ \frac{a}{2} \ + \ h \ + \ \frac{a}{\sqrt{3}} + 1,0 \ \text{cm} \ + \ 0,7 \ \text{cm} ) \)
Die Funktion \( \tilde{M} \) hängt also von zwei Variablen - a und h - ab und gilt unter der Annahme, dass die Klebefalze für beliebige (realistische) Größen immer die gleichen Abmessungen haben, für beliebige Höhe und Breite. Für die tatsächliche 1-Liter-Safttüte gilt, dass diese im quaderförmigen Teil ein Volumen von 1000 cm³ haben, also die Gleichung \( V \ = \ a^2 \cdot h \ = \ 1000 \text{cm³} \) gelten soll. Wie in der ersten Modellierung lösen wir diese Gleichung nach h auf und setzen diese in M ein. Damit erhalten wir eine Materialfunktion, die nur von der Variablen a abhängt.

Bei einer handelsüblichen Safttüte lauten die Abmessungen: a = 7 cm und h = 19,5 cm. Damit ergibt sich ein theoretisches Volumen von nur \( V \ = \ 7^2 \cdot 19,5 = 955,5 \ [\text{cm³}] \). Dafür sieht man an einer gefüllten Safttüte, dass die Seitenflächen sich etwas nach außen wölben und nicht exakt einen Quader bilden. Außerdem ermöglicht das Giebeldach ebenfalls einen kleinen Teil des noch fehlenden Volumens aufzunehmen (allerdings nur bis zur Unterkante der Ausgießöffnung, damit nach dem Öffnen nicht sofort ein Teil des Safts ausläuft). Ohne dies genauer zu untersuchen, gehen wir davon aus, dass durch den Wölbungseffekt die fehlenden 44,5 cm³ Volumen in der Safttüte untergebracht werden können und kein Betrug vorliegt.
Wir berücksichtigen den Wölbungseffekt, indem wir das Volumen für den quaderförmigen Teil auf 955,5 cm³ reduzieren, aber weiterhin eine mathematisch exakte Quaderform betrachten. Die endgültige Materialfunktion lautet nun:
\( \begin{align} M(a) \ & = \ (1,0 \ \text{cm} \ + \ 4 \cdot a)\cdot \\ & \cdot (1,4 \ \text{cm} + \ \frac{a}{2} \ + \ \frac{955,5 \text{cm³}}{a^2} + \ \frac{a}{\sqrt{3}} + 1,0 \ \text{cm} \ + \ 0,7 \ \text{cm} ) \end{align} \)
\( \begin{align} M(a) \ & = \ (12,9 \ \text{cm} \ + \ 1 \ \text{cm} \cdot \frac{1}{\sqrt{3}} )\cdot a \ + \ ( \frac{4}{\sqrt{3}} \ + \ 2)\cdot a^2 \ + \\ & + \ 4 \cdot \frac{955,5 \text{cm³}}{a} \ + \ 1 \ \text{cm} \cdot \frac{955,5 \text{cm³}}{a^2} \ + \ 3,1 \ \text{cm} ) \end{align} \)
Analog zur ersten Modellierung könnten wir zu dieser Funktion die erste und zweite Ableitung bestimmen, um ein Extremum zu finden und dieses darauf zu prüfen, ob es ein Minimum ist. Wir verzichten hier darauf und untersuchen die Funktion stattdessen dynamisch mit einer GeoGebra-Simulation. Die Komplexität der Funktion deutet schon an, dass es nicht so leicht ist, mit Standardverfahren Nullstellen der Ableitung zu bestimmen und daher sowieso numerische Näherungsverfahren und der Einsatz von Computern nötig sind.
Die Genauigkeit ist hier für die Seitenlänge a auf eine Nachkommastelle eingestellt. Bei einer Stanzgenauigkeit von 0,1 cm in der realen Situation genügt diese Genauigkeit. Aus der Simulation erhalten wir einen minimalen Materialverbrauch von 873,7 cm² bei einer Seitenlänge von 7,3 cm der quadratischen Grundfläche. Daraus resultiert die zugehörige Höhe von 17,9 cm.
Im Vergleich mit einer echten Giebeldachtüte stellt man fest, dass diese eine Seitenlänge von nur 7 cm hat, die Höhe beträgt 19,5 cm und der Materialverbrauch 874,1 cm². Damit kann die reale Safttüte unter den Herstellungsbedingungen als materialminimal angesehen werden kann.

5.6. Kurvendiskussion


Mit Hilfe der Differenzialrechnung lassen sich Funktionen auf Eigenschaften wie Monotonieverhalten, Krümmungsverhalten oder Extremwerte hin untersuchen. Dabei können die Eigenschaften einer Funktion von Lernenden rein qualitativ untersucht, oder durch Berechnung auch quantitativ bestimmt werden. Eine solche Diskussion lässt sich einerseits durch Vorgabe einer Funktion motivieren oder andererseits durch Vorgabe bestimmter Eigenschaften, was die Konstruktion einer Funktion ermöglicht. Letzterer Fall ist für Modellierungsprozesse von besonderer Bedeutung. Ein entscheidender Schritt im Rahmen der Kurvendiskussion ist der Übergang von einer lokalen Betrachtung einzelner „Stellen“ zu einer globalen Sichtweise der Funktion und ihrer Ableitungsfunktion(en) als Objekte und der Verbindungen zwischen diesen. Die klassische Kurvendiskussion wurde häufig als zu kalkülhaft und durch technologische Entwicklungen (Funktionenplotter o.Ä.) unter praktischen Gesichtspunkten als zunehmend unnötig kritisiert; dennoch stellt sie aus theoretischer Sicht weiterhin ein wichtiges Mittel zum Erlernen des Umgangs mit Funktion dar.

Monotonie
Im Kapitel Eigenschaften von Funktionen haben wir das Monotonieverhalten von Funktionen kennengelernt. Dies werden wir nun mit dem Differenzierbarkeitsbegriff verknüpfen. Dadurch ergeben sich unter anderem die folgenden Monotoniekriterien:
Die Funktion \(f\) sei auf \([a,b]\) differenzierbar. Dann gilt:
Wenn \( \forall x\in [a,b] \;\; f'(x) > 0 \), dann wächst \(f\) auf \([a,b]\) streng monoton
und
wenn \( \forall x\in [a,b] \;\; f'(x) < 0 \), dann fällt \(f\) auf \([a,b]\) streng monoton.
Achtung! Die Umkehrung dieses Satzes ist allerdings nicht richtig. Eine Funktion kann streng monoton steigen, obwohl ihre Ableitung eine Nullstelle hat.
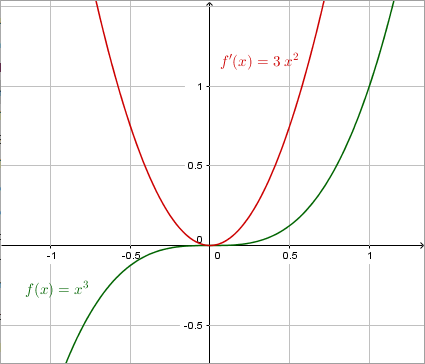
Schränkt man die Forderung lediglich auf Monotonie ein (und nicht auf strenge Monotonie), so gilt auch die Umkehrung der Aussage (vgl. Satz 3 in Kapitel 5.4):
Die Funktion \(f\) sei auf \([a,b]\) differenzierbar. Dann gilt die folgende Äquivalenz:
\( \forall x \in [a,b] \; \; f'(x) \leq 0 \Leftrightarrow f \) ist auf \( [a,b] \) monoton fallend.

Krümmungsverhalten
Stellen wir uns vor einen differenzierbaren Graphen wie eine Streckenkarte von oben herab entlang zu fahren, dann sind die lokalen Maxima und Minima diejenigen Stellen, an denen wir am meisten mit dem Lenkrad einschlagen müssen. Dabei kann man unterscheiden, ob wir das Lenkrad nach rechts oder links einschlagen müssen.
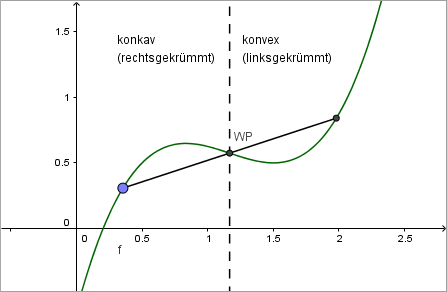
Eine Funktion \(f\) heißt auf einem Intervall \([a,b]\) streng konvex (d.h., ihr Graph ist dort strikt links-gekrümmt), wenn für alle \(x_1,x_2,x_3 \in [a,b]\) mit \(x_1 < x_2 < x_3\) die folgende Beziehung gilt:
\[ \frac{f(x_2) - f(x_1)}{x_2 - x_1} < \frac{f(x_3) - f(x_2)}{x_3 - x_2} \]
Anschaulich bedeutet dies, dass von zwei beliebigen aneinandergrenzenden Sekanten die jeweils rechte stärker steigt (steiler ist) als die jeweils linke. (Es liegt also ein „Links-Knick“ vor.)
\[ \frac{f(x_2) - f(x_1)}{x_2 - x_1} > \frac{f(x_3) - f(x_2)}{x_3 - x_2} \]
Eine Funktion \(f\) ist auf einem Intervall genau dann konvex, wenn \(-f\) konkav ist.
Die Krümmung eines Grafen kann man allerdings nicht direkt mittels der Steigung herausfinden. Wir benötigen hierfür die Steigung der Ableitung, also die zweite Ableitung.
Dies wollen wir uns anhand eines einfachen Beispiels überlegen: Sei \(f: \mathbb{R} \to \mathbb{R}\) mit \( f(x)=x²+4 \). Diese Parabelfunktion ist linksgekrümmt, wenn wir sie entlang fahren, mit maximaler Krümmung im Punkt \( (0|4) \). Da der Graph für \( x \)- Werte kleiner als 0 fällt und größer als 0 steigt, ist der Graph der Ableitung für \( x \)-Werte kleiner als 0 negativ und größer als 0 positiv (und in \(x=0\) auch 0, da ein Minimum vorliegt). Wenn wir von dieser Funktion wiederum die Ableitung bestimmen, dann muss der Wert in \( x=0 \) größer als 0 sein. Denn die Steigung ist in diesem Punkt größer als 0, da der Graph von unterhalb der \(x\)-Achse nach oberhalb der \(x\)-Achse verläuft wie im Bild zu sehen ist.
Definition 1.
Sei \(f: I \subset \mathbb{R} \to \mathbb{R}\) zweimal differenzierbar. Dann ist der Graph von \( f \) im Intervall \( I \) rechtsgekrümmt genau dann, wenn \( f''(x)<0 \) für \(x \in I \) und linksgekrümmt im Intervall \( I \) genau dann, wenn \( f''(x)>0 \) für \(x \in I \). Im Fall \( f''(x) \) hat der Graph in diesem Punkt keine Krümmung bzw. die Krümmung 0.
Hinweis: Mithilfe der zweiten Ableitung lässt sich nur die Art der Krümmung bestimmen, jedoch nicht deren Wert. Dieser ist nur proportional zur zweiten Ableitung!
Wir können also zusammenfassen:
Eine auf einem Intervall \([a,b]\) differenzierbare Funktion ist dort genau dann streng konvex (bzw. streng konkav), wenn ihre erste Ableitung streng monoton steigend (bzw. streng monoton fallend) ist.
In Kombination mit dem Monotoniekriterium ergibt sich, dass eine zweifach differenzierbare Funktion, deren zweite Ableitung auf einem Intervall positiv ist, dort einen strikt links-gekrümmten Graphen besitzt.Mithilfe der Krümmung können wir nun Kandidaten für lokale Extrema, die wir mittels Nullstellenbestimmung der Ableitung identifiziert haben, genauer betrachten. Haben wir eine nach rechts gekrümmte Kurve der Funktion \( f \) und haben wir im Punkt \(x_0\) die Steigung 0, so müssen die Funktionswerte links von \( x_0 \) kleiner als \( f(x_0) \) sein. Analog müssen die Funktionswerte rechts von \( x_0 \) wieder kleiner als \( f(x_0) \) sein. Bei \( x_0 \) handelt es sich demnach um ein lokales Maximum. Genauso kann man linksgekrümmt und lokales Minimum miteinander verknüpfen.
Diese Erkenntnis wollen wir kurz und prägnant festhalten.

Sei \(f: I \subset \mathbb{R} \to \mathbb{R}\) zweimal differenzierbar. Zudem sei \( f'(x_0)=0 \). Dann hat \( f \) in \( x_0 \) ein lokales Maximum, wenn \( f''(x_0)<0.\) lokales Minimum, wenn \( f''(x_0)>0.\) Im Fall \( f''(x_0) \) liegt kein Extremum vor.

Beispiel 1'
Sei \(f: \mathbb{R} \to \mathbb{R}\) definiert als \[f(x) = x^3 -3x + 1.\] Dann ist \[f'(x) = 3x^2-3\].
Wir haben die Kandidaten als \( x_0 = -1 \) und \( x_1 = 1 \) schon berechnet. Wir bestimmen weiter die zweite Ableitung der Funktion \(f \) \[ f''(x) = 6x. \] Nun ist \( f''(-1) = -6 \) und \( f''(1)=6 \). Demnach hat \( f \) in \( x_0 \) ein lokales Maximum und in \(x_1 \) ein lokales Minimum - wie wir auch schon graphisch gesehen haben.

Kurvendiskussion
Hier ein Beispiel für eine ausführliche Kurvendiskussion.
- Nullstellen
- Extremwerte
- Krümmungsverhalten
- Symmetrie und Verhalten im Unendlichen
- Zeichnen des Graphen.
Wir führen im Folgenden eine ausführliche Kurvendiskussion für die Funktion \(f\colon \mathbb{R} \to \mathbb{R}, x \mapsto -x^4+8x^2-16 \) aus.
Nullstellen:
Gesucht sind alle Punkte \( x \in \mathbb{R} \) mit \( f(x)=0 \). Da es es sich bei \( f \) um ein Polynom vierten Grades handelt, gibt es kein (praktikables) allgemeines Verfahren. Wir wollen deshalb zwei Varianten bespechen - natürlich würde eine davon genügen.
Variante 1: Wir erkennen, dass im Funktionsterm nur gerade Exponenten auftauchen und substituieren ("ersetzen") \( x^2 \) durch \( u \). Wir erhalten dann
\[f(u) = -u^2+8u-16. \]
Nun haben wir ein Polynom zweiten Grades, dessen Nullstellen wir z.B. mit der Mitternachtsformel oder dem Satz von Vieta finden können. Mit der Mitternachtsformel folgt \( u_{1/2}=\frac{-8\pm \sqrt{8^2-4\cdot(-1)\cdot(-16)}}{-2} = 4.\)
Wir haben also nur eine (doppelte) Nullstelle.
Zuletzt müssen wir noch resubstituieren, um die Nullstellen unserer ursprünglichen Funktion zu finden. Mit der Substitutionsbedingung folgt dann \( x^2 = u = 4 \), also \( x_1 = 2 \) und \( x_2 = -2 \).
Da wir beim Funktionsterm\( f(u)=-u^2+8u-16 \) eine doppelte Nullstelle erhalten, resubstituieren wir diese auch doppelt und erhalten daher je zweimal die Nullstellen \( x_1 \) und \( x_2 \). Es handelt sich dabei also jeweils um doppelte Nullstellen.
Variante 2: Wie im Kapitel zur Berechnung der Nullstellen dargestellt, kann man auch Nullstellen raten. Hierbei genügt es Teiler des konstanten Glieds zu untersuchen. Bei uns sind das die Zahlen \( -16, -8, -4, -2, -1, 1, 2, 4, 8, 16. \) Es bietet sich dabei an, mit den betragmäßig kleineren Zahlen zu beginnen und wir erhalten so z.B. \( f(2) = 0 \). Eine Nullstelle ist also sicher schon \( x_1 = 2\).
Wir können nun den Linearfaktor \( (x-x_1)=(x-2) \) mittels Polynomdivision abspalten (vgl. Kapitel 3.4):
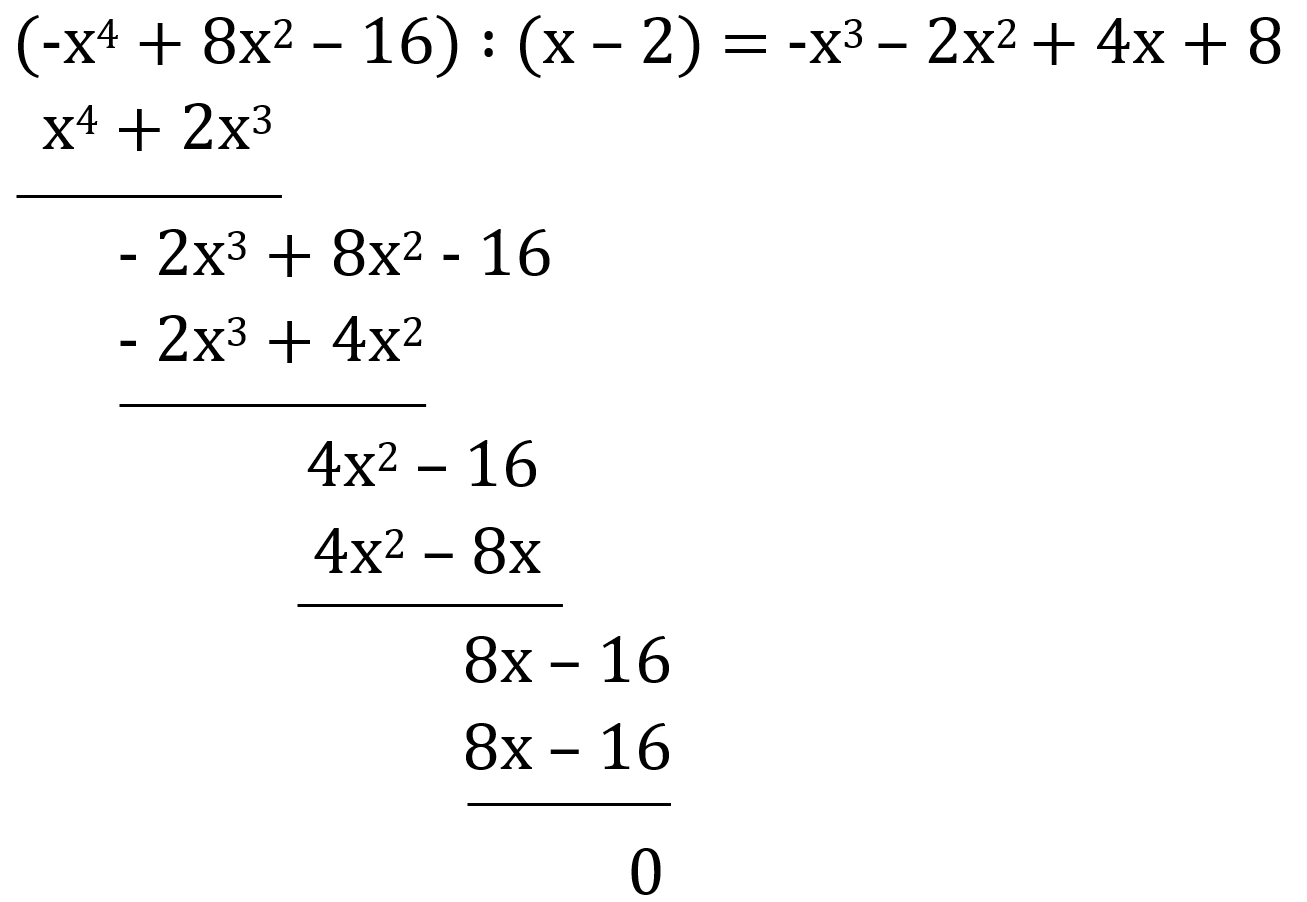
Den so erhaltenen Term \( -x^3 -2x^2 + 4x + 8 \) analysieren wir wieder auf Nullstellen. Wieder raten wir die Nullstelle \( x_1 = 2 \), da \( 2 \) ein Teiler von \( 8 \) ist und \( 2 \) eingesetzt Null ergibt. Durch nochmalige Polynomdivision erhalten wir \( -x^2 - 4x -4 \).
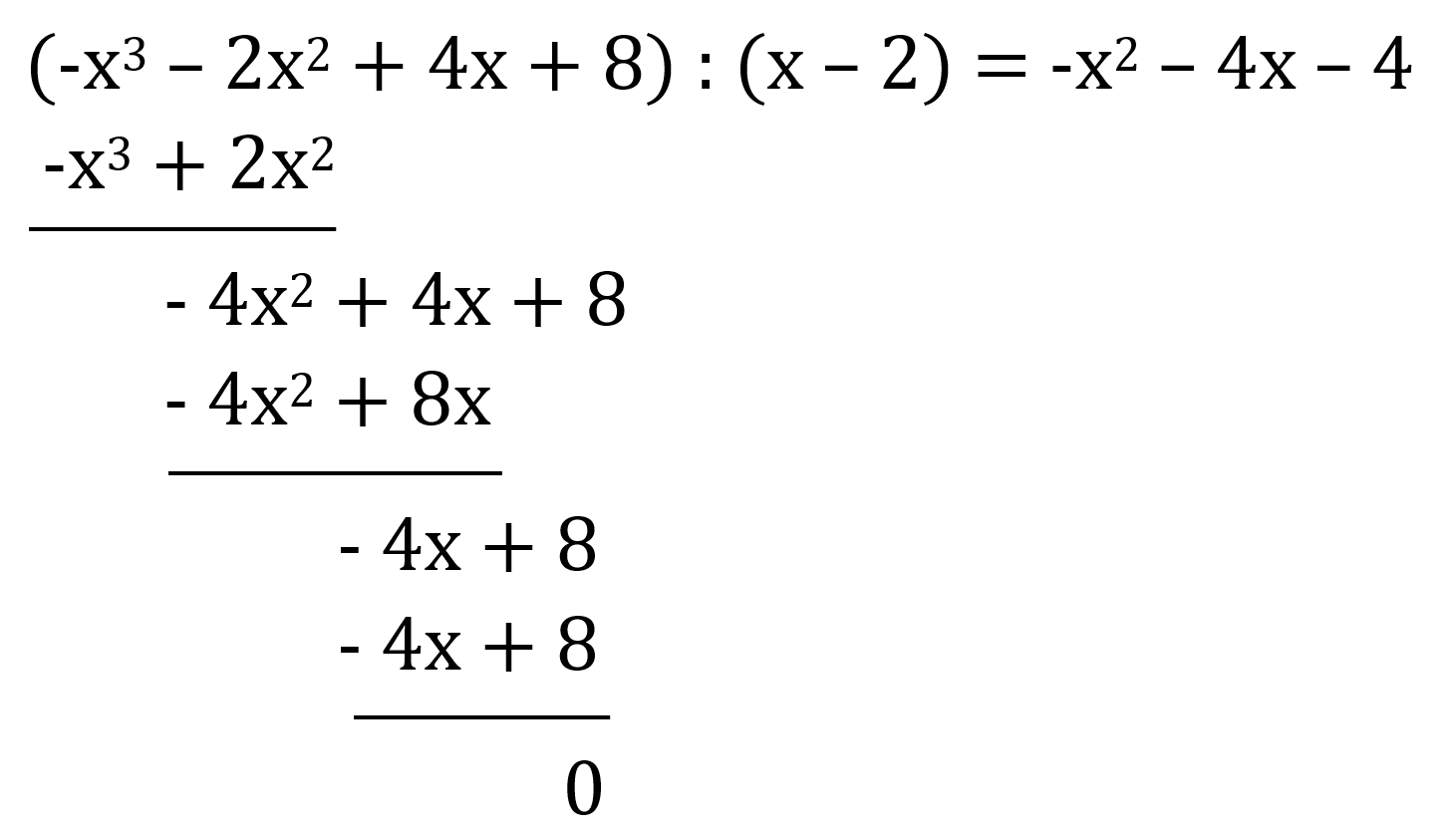
Hier kann man weiter z.B. wieder mit Mitternachtsformel vorgehen oder ein \( -1 \) ausklammern, sodass wir die doppelte Nullstelle \( x_2 = -2 \) bzw. den Term \( -(x+2)^2 \) erhalten.
Zusammengefasst kennen wir die Darstellung von \( f \) in Linearfaktoren, nämlich \( f(x) = -(x-2)^2 \cdot (x+2)^2 \), und wir wissen, dass wir zwei doppelte Nullstellen bei \( x_1 = 2\) sowie \( x_2 = -2 \) vorliegen haben.
Extremwerte:
Für Extremstellen müssen wir nach Satz 1 aus Kapitel 5.4 einerseits Punke betrachten, in denen die Ableitung nicht existiert (also insbesondere Randpunkte), sowie die Nullstellen der Ableitungsfunktion.
Da es sich bei \( f \) um ein Polynom handelt, das auf \( \mathbb{R} \) definiert und differenzierbar ist, gibt es keine Punkte, in denen die Ableitung nicht definiert ist.
Für den zweiten Fall bestimmen wir zunächst \( f' \) mittels der Ableitungsregel für Polynome als \( f'(x)=-4x^3 + 16x. \) Wir bestimmen die Nullstellen der Ableitung:
\( f'(x) = 0 \Leftrightarrow -4x^3+16x=0 \Leftrightarrow x \cdot (-4x^2+16) = 0 \Leftrightarrow x \cdot (-4) \cdot (x^2 - 4) \)
\( \Rightarrow \) Da ein Produkt null ist, genau dann wenn einer der Faktoren null ist, sind unsere Kandidaten also \( x_0 = 0, x_1 = 2 \) und \( x_2 = -2. \)
Um zu bestimmen, ob es sich dabei wirklich um lokale Exrema handelt und falls ja um welche Art, nutzen wir die zweite Ableitung, die wir zunächst bestimmen: \( f''(x)= - 12x^2+16. \)
Wir berechnen nun die Werte unserer drei Kandidaten und erhalten \( f''(0) = 16>0, f''(-2)=f''(-2)=-32<0 \).
Da keiner der drei Funktionswerte gleich \( 0 \) ist, handelt es sich (nach dem hinreichenden Kriterium für lokale Extrema), um lokale Extrema, wobei in \( x_0 \) ein lokales Minimum und in \( x_1 \) sowie \( x_2 \) je ein lokales Maximum vorliegt (aufgrund der Vorzeichen).
Zuletzt müssen wir die lokalen Extrema als Punkte angeben, d.h. wir müssen noch deren y-Koordinaten berechnen. Von \( x_1 \) und \( x_2 \) wissen wir, dass es sich um Nullstellen handelt, also \( y_1 = y_2 = 0 \). Für \( y_0 \) erhalten wir \( y_0 = f(x_0) = f(0) = -16 \).
Zusammenfassend haben wir ein lokales Minimum bei \( (0|-16) \) und zwei lokale Maxima bei \( (-2|0) \) und \( (2|0). \)
Krümmungsverhalten: Um das Krümmungsverhalten zu bestimmen, suchen wir nach Wendepunkten, d.h. Punkten an denen sich die Krümmung der Funktion ändert. Da wir die Art der Krümmung über das Vorzeichen der zweiten Ableitung bestimmen können, muss hierfür die zweite Ableitung gleich Null sein.
Aus \( f''(x)=-12x^2+16 = 0 \) erhalten wir die Gleichung \( x^2= \frac43 \), d.h. \( x = \pm \frac{2 \cdot \sqrt3}{3}. \)
Daraus können wir schließen, dass \( f \) innerhalb der drei Intervalle \( (- \infty, - \frac{2 \cdot \sqrt3}{3}) \) , \( (- \frac{2 \cdot \sqrt3}{3}, \frac{2 \cdot \sqrt3}{3}) \) und \( (\frac{2 \cdot \sqrt3}{3}, \infty ) \) jeweils dasselbe Krümmungsverhalten besitzt; dieses müssen wir nun noch bestimmen.
Dazu setzen wir jeweils einen beliebigen (schönen) Wert aus dem jeweiligen Intervall in die zweite Ableitung ein. Wir nutzen hierfür \( -2, 0 \) und \( 2 \), da \( -2 < - \frac{2 \cdot \sqrt3}{3} \), \( 2 > \frac{2 \cdot \sqrt3}{3} \) und \( 0 \in (- \frac{2 \cdot \sqrt3}{3}, \frac{2 \cdot \sqrt3}{3}) \) und wir diese Werte schon bei den lokalen Extrema berechnet haben:
\( f''(-2)= f''(2)= -32 < 0\) und \(f''(0)=16>0 \).
D.h. im ersten und dritten Intervall ist die Funktion rechtsgekrümmt und im zweiten Intervall linksgekrümmt.
Abschließend bestimmen wir noch die \(y\)-Koordinaten der Wendepunkte. Es ist \( f (\pm \frac{2 \cdot \sqrt3}{3}) = - \frac{64}{9}. \) Also liegen die Wendepunkte bei \( (- \frac{2 \cdot \sqrt3}{3}|- \frac{64}{9}) \) und \( (\frac{2 \cdot \sqrt3}{3}|- \frac{64}{9}) \).
Symmetrie und Verhalten im Unendlichen: Für die Betrachtung der Symmetrieeigenschaften des Graphen betrachten wir uns \( f(-x) \). Es gilt dabei in unserem Fall, dass
\( f(-x) = (-1) \cdot (-x)^4+8 \dot (-x)^2-16=-x^4+8x^2-16 = f(x). \)
D.h. die Funktion ist achsensymmetrisch bzgl. der \(y\)-Achse (Dies hat man auch schon anhand der Lage der Nullstellen, lokalen Maxima, etc. vermuten können).
Das Verhalten im Unendlichen betrachten wir zunächst im Positiven. Es gilt dabei
\( \lim \limits_{x \to \infty} f(x) = \lim \limits_{x \to \infty} -x^4+8x^2-16 = - \infty , \)
denn da es sich bei \( f \) um ein Polynom handelt, hängt das Verhalten lediglich vom Monom mit dem höchsten Exponenten ab; hier \(-x^4\) und es gilt \( \lim \limits_{x \to \infty} -x^4 = - \infty \).
Für die Betrachtung im Negativen können wir nun argumentieren, dass die Funktion achsensymmetrisch ist und deshalb \( \lim \limits_{x \to - \infty} f(x) = \lim \limits_{x \to - \infty} f(x) = - \infty \) gelten muss. Man könnte aber auch wieder das Verhalten von \( -x^4 \) im Negativen betrachten.
Zeichnen des Graphen: Aus den bisherigen Informationen können wir nun einen Graphen skizzieren bzw. zeichnen. Hierfür trägt man die Nullstellen, lokalen Extrema und Wendepunkte in ein Koordinatensystem ein. Mit den zusätzlichen Infos, dass \( \lim \limits_{x \to \pm \infty} f(x) = - \infty \) und \(f\) achsensymmetrisch zur \(y\)-Achse ist, erhalten wir den nebenstehenden Graphen.

5.7. Aufgaben


Aufgabe 1:
Bestimmen Sie die Ableitung der Funktionen \(f\), \(g\), \(h\):
- \(f(x) = (x^3 - x^7)^{11}\)
- \(g(x) = \frac{x^3 + 1}{\sqrt{1+x^2}}\)
- \(h(x) = \cos(2x) \cdot \sin(5x)\)
Aufgabe 2:
Leiten Sie die Terme nach \(x\) ab:
- \(\cos(x^3)\)
- \(\sqrt{x^2 + x^4}\)
- \(\cos((x^2 + x^4)^\frac{3}{2})\)
Aufgabe 3:
Bestimmen Sie die Ableitungen der Funktionen:
- \(f(x) = \ln(\cos(x))\) mit \( - \frac{\pi}{2} < x < \frac{\pi}{2}\)
- \(g(x) = \frac{\sin(x) + \cos(x)}{\sin(x) - \cos(x)}\) mit \(\sin(x) - \cos(x) \ne 0\)
Ein Punkt bewegt sich auf der x-Achse. Sein Ort \(x\) in Abhängigkeit von der Zeit \(t\) ist gegeben durch: \(x = 3t + 2t^2\)
Bestimmen Sie die Geschwindigkeit \(v(t)\) des Punktes in Abhängigkeit von \(t\).
Hinweis: Die Durchschnittsgeschwindigkeit eines Objekts im Zeitintervall \([t; t+h]\) ist die Änderung des Ortes dividiert durch die Änderung der Zeit.
\(v_{Schnitt} = \frac{\Delta x}{\Delta t} = \frac{x(t+h) - x(t)}{h} [\frac{m}{s}]\)
Die Geschwindigkeit \(v(t)\) des Objekts zur Zeit \(t\) ist der Grenzwert der Durchschnittsgeschwindigkeit für \(h \rightarrow 0\).
Ein Kanuclub möchte ein Grundstück am Ufer eines Flusses kaufen. In der Mitte der \(460m\) langen geraden Begrenzungslinie ist das Grundstück \(50m\) breit. Bestimmen Sie den Graphen einer Funktion, der die Uferlinie möglichst gut beschreibt. Verwenden Sie ein geeignetes Koordinatensystem.
Ein Zinnkrug ist zylinderförmig und hat eine kreisförmige Grundfläche. Wir gehen von einem festen Volumen \(V\) aus. Die Höhe des Kruges bezeichnen wir mit \(h\) und den Radius der Grundfläche mit \(r\).
- Welche Abmessungen sollte der Krug haben, damit der Materialverbrauch möglichst gering ist?
- Bewerten Sie die Lösung unter a) unter praktischen Gesichtspunkten.

6. Integralrechnung


- Grundlagen zur Integralrechnung
- Hauptsatz der Integral und Differentialrechnung
- Integrale Elementarer Funktionen
- Integrationsregeln
- Anwendungen

6.1. Grundlagen


Definition 1:
Es sei \([a,b]\) ein echtes kompaktes Intervall. Eine Zerlegung von I ist ein (n+a)-Tupel \[Z = ( x_0, x_1, x_2, ..., x_{n-1}, x_n) \] mit einer beliebigen natürlichen Zahl n und reellen Zahlen \(x_0, x_1, x_2, ..., x_{n-1}, x_n \), die \[x_0 < x_1 < x_2 <...<x_{n-1}< x_n = b\] erfüllen. Die Punkte \(x_{i} \) heißen Teilpunkte der Zerlegung \(Z\), und die positive Zahl \[ \|Z\| := \max_{1 \leq i \leq n} (x_i - x_{i-1}). \] heißt die Feinheit der Zerlegung.Da \(f\) beschränkt ist, existieren auf jedem Teilintervall \([t_{i-1},t_i]\) Supremum (\(M_i\)) und Infimum (\(m_i\)) von \(f\).
Dann heißen
\[\sum^{n}_{i=1} M_i\cdot (t_i - t_{i-1})\]
Obersumme und
\[\sum^{n}_{i=1} m_i\cdot (t_i - t_{i-1})\]
Untersumme von \(f\) zur Zerlegung \(Z\).
Mit deren Hilfe lässt sich das Integral definieren:

Definition 2
\(f\) sei eine auf einem abgeschlossenen Intervall \([a,b]\subset\mathbb{R}\) definierte und dort beschränkte Funktion. Ist das Supremum \(S\) aller über \([a,b]\) gebildeten Untersummen gleich dem Infimum \(I\) aller über \([a,b]\) gebildeten Obersummen, so heißt \(S=I\) das bestimmte Integral von \(f\) über dem Intervall \([a,b]\) und wird mit
\[\int^{b}_a f(x)\;dx\]
bezeichnet. In diesem Fall heißt die Funktion \(f\) integrierbar über \([a,b]\).
Es gilt: \(\begin{eqnarray*}\int\limits^a_a f(x)\,\mathrm d{x} & := & 0 \])

Falls \[ \lim_{n\to\infty} U_n = \lim_{n\to\infty} O_n, \] dann nennt man diese Zahl das bestimmte Integral von \(f\) über \([a,b]\). Sie wird bezeichnet mit: \[ \int^{b}_a f(x)\;dx \] \(f\) heißt in diesem Fall integrierbar über \([a,b]\).
Satz 1 (Integrabilitätskriterium von Riemann)
\(f\) sei eine auf einem abgeschlossenen Intervall \([a,b]\subset\mathbb{R}\) definierte und dort beschränkte Funktion. Dann sind folgende Aussagen äquivalent:
\( f \)ist Riemann-integrierbar.
und
Für jedes \(\mathcal{E}\) gibt es eine Partition \(P\), für die \(O_n (f,P)-U_n (f,P) < \mathcal{E}\) gilt.

Satz 1 (Integrierbarkeit von Funktionen)
- Ist \(f\) auf \([a,b]\) monoton und beschränkt, so ist \(f\) auf \([a,b]\) integrierbar.
- Ist \(f\) auf \([a,b]\) stetig, so ist \(f\) auf \([a,b]\) integrierbar.
Eine Funktion heißt monoton, wenn sie monoton fallend oder monoton steigend ist.

6.2. Eigenschaften des Integrals


Eigenschaften des Integrals:
Die Addition und skalare Multiplikation von Funktionen lässt sich mit dem Differenzieren vertauschen. Es gilt
\[(a \cdot f(x) + b\cdot g(x))' = a \cdot f'(x) + b\cdot g'(x).\]
Gleiches gilt auch beim Integrieren:

Additivität und Homogenität
Additivität:\(\int (f(x) + g(x)) \,\mathrm d x = \int f(x) \,\mathrm d x + \int g(x) \,\mathrm d x\).
Homogenität:
\(\int c \cdot f(x) \,\mathrm d x = c \cdot \int f(x) \,\mathrm d x\).
Zusammengefasst wird geschrieben:
\[\int a \cdot f(x) + b\cdot g(x)\,\mathrm{d}x = a \int f(x)\,\mathrm{d}x + b\int g(x)\,\mathrm{d}x.\]
Das Integral stellt eine lineare Operation auf dem Raum der integrierbaren Funktionen dar.
Beispiel 1:
\[\int 3 x^2 + 5 \,\mathrm d x = 3 \cdot \int x^2 \,\mathrm d x + 5\int 1 \,\mathrm d x \\ = 3 \cdot \frac{1}{3} x^3 + 5 x = x^3+5x+c,\,c\in\mathbb{R}.\]
Wieder betrachten wir integrierbare Funktionen \(f\). Aus der Herleitung des bestimmten Integrals über \(f\) lassen sich weitere Eigenschaften des Integrals ableiten.

Vertauschung von Grenzen
\[ \int \limits^a_b f(x)\,\mathrm{d}x := - \int\limits^b_a f(x)\,\mathrm{d}x\]

Positivität
Gilt für den Integranden \(h(x)\geqslant 0\) für \(x\in[a,b] \) so ergibt sich für das Integral
\[\int_a^b h(x)\, \mathrm{d}x \geqslant 0.\]

Monotonie des Integrals
Gilt an jedem Punkt \(x \in [a,b]\)
\[ f(x)\leqslant g(x) \] so gilt dies auch für die bestimmten Integrale
\[ \Rightarrow \int_a^bf(x)\, \mathrm{d}x\leqslant \int_a^bg(x)\, \mathrm{d}x. \]
Als spezielle Folgerung ergibt sich mit der letzten Aussage aus der Eigenschaft \(f(x) \leq |f(x)|\) die Aussage
\[\pm \int_a^bf(x)\, \mathrm{d}x \leqslant \int_a^b |f(x)|\, \mathrm{d}x.\]
Auf der linken Seite können wir nun auch den Betrag schreiben und erhalten:
\[\left| \int_a^bf(x)\,\mathrm{d}x\right| \leqslant \int_a^b|f(x)|\,\mathrm{d}x.\]

Mittelwerte
Oft wird die Integration geometrisch als der Flächeninhalt unter einer Funktion auf einem bestimmten Intervall interpretiert, wie die rote Fläche in der Graphik. In der Graphik ist aber auch ein Rechteck dargestellt, das den gleichen Flächeninhalt \(A\) besitzt, wie die rot dargestellte Fläche,\[A= \int\limits_a ^b f(x) \,\mathrm d x.\] Das Rechteck der Höhe \(h\) und Länge \(b-a\) besitzt den Flächeninhalt \(A_R=h\cdot(b-a)\). Dieser Flächeninhalt \(A_R\) soll gleich dem der Fläche unter der Funktion \(f\) zwischen den Werten \(a\) und \(b\). Es gilt also: \[A_R=h (b-a) = \int \limits _a^b f(x) \,\mathrm d x=A\]und somit \[ \quad h = \frac{1}{b-a} \cdot \int \limits _a ^b f(x) \,\mathrm d x.\] \(h\) ist dann der Mittelwert der Funktion auf dem Intervall \([a,b]\).
Außer dem linearen gibt es auch noch den quadratischen Mittelwert \(\sqrt{\frac{1}{b-a} \int \limits _a^b f^2(x) \,\mathrm d x}\), der zum Beispiel verwendet wird, um den Effektivwert einer Spannung zu berechnen.
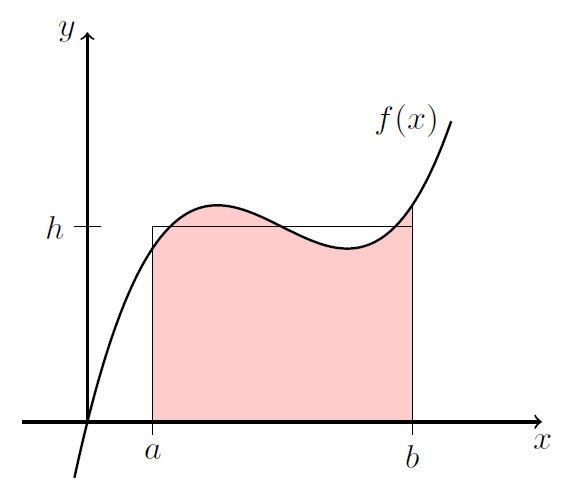
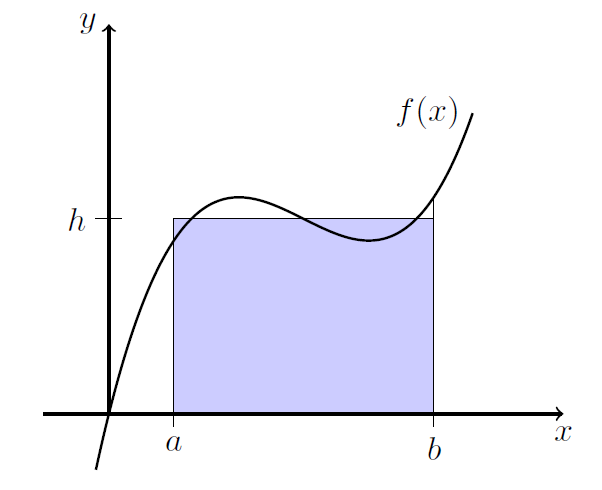

Satz 2 (Mittelwertsatz der Integralrechnung)
Sei \(f\) eine auf \([a,b]\) stetige Funktionen für alle \(x \in [a,b]\), dann gibt es eine Zwischenstelle \(\overline{x} \in [a,b]\) mit
\[\int\limits^b_a f (x) \,\mathrm d{x} =f (\overline{x}) \cdot(b-a).\]

Das Integral als Abbildung
Das bestimmte Integral von \(a\) bis \(b\) über eine Funktion \(f\) können wir als eine Abbildung auffassen. Die Menge der über \([a,b]\) integrierbaren Funktionen sei mit \(I([a,b])\) bezeichnet. Dann ist folgende Interpretation möglich:
\[\int_a^b:I[a,b] \to \mathbb R\qquad \mbox{mit} \qquad f\mapsto \int_a^b f(x)\mathrm d x.\]
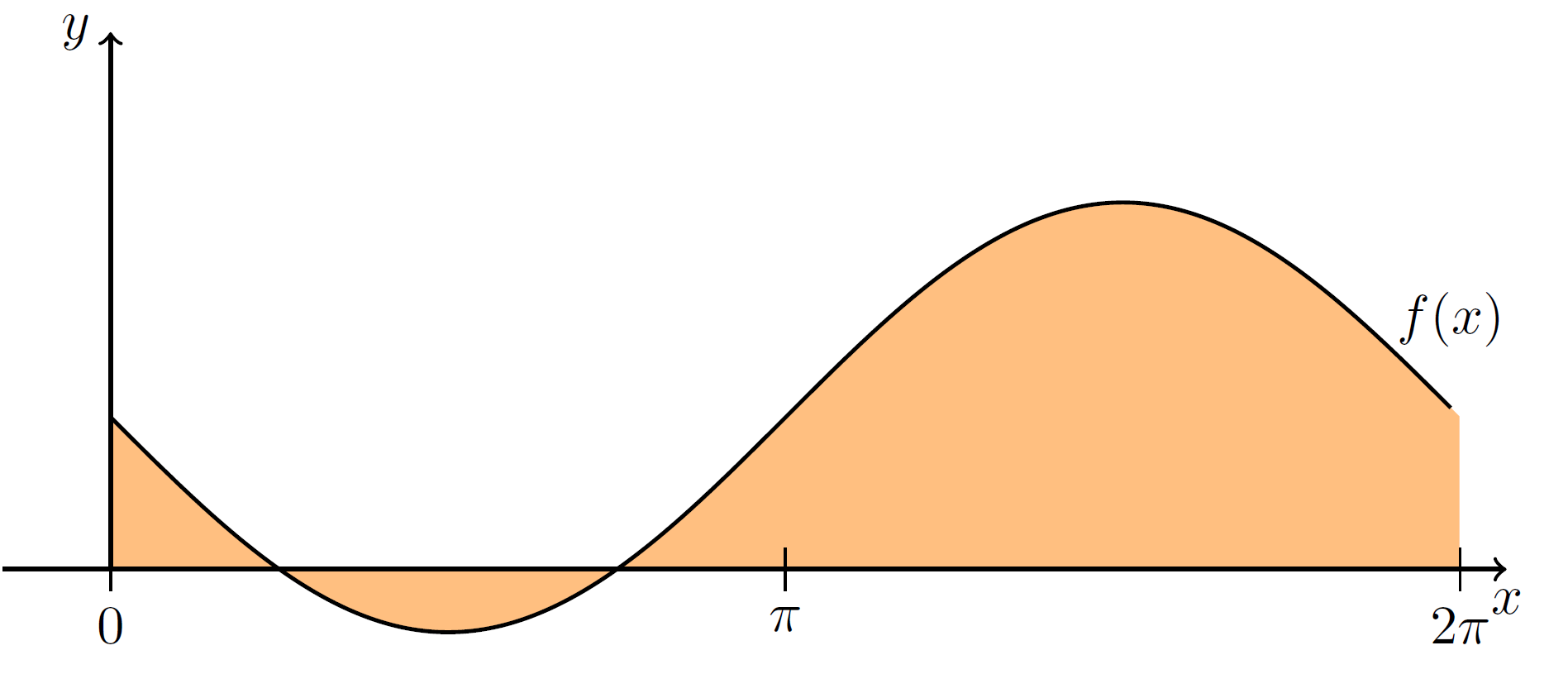

Hierzu sind bei Berechnung einer Flächen zwischen einem Funktionsgraphen und der x-Achse in einem bestimmten Intervall drei Fälle zu unterscheiden:
1. Der Graph verläuft oberhalb der x-Achse.
2. Der Graph verläuft unterhalb der x-Achse.
3. Der Graph schneidet die x-Achse (ggf. mehrmals)
Im ersten Fall entspricht der Wert des Integrals gerade dem Flächeninhalt zwischen x-Achse und Funktionsgraph. (Man spricht auch von einer „positiven Normalfläche“.)
Im zweiten Fall entspricht der Betrag des Integralwertes gerade dem Flächeninhalt zwischen x-Achse und Funktionsgraph. (Hier wird auch von einer „negativen Normalfläche“ gesprochen.)
Im dritten Fall unterscheiden sich der Integralwert und sein Betrag allerdings vom Flächeninhalt zwischen x-Achse und Funktionsgraph. Um hier den tatsächlichen Flächeninhalt zu bestimmen, ist es notwendig, das betrachtete Gesamt-Intervall in Teilintervalle zwischen den Nullstellen der Funktion zu unterteilen. Anschließend kann dieser Fall in den jeweiligen Intervallen auf die Fälle 1) und 2) zurückgeführt werden.

6.3. Hauptsatz der Integral und Differentialrechnung

In dem vorherigem Kapitel wurde aus der Kenntnis eines Intervalls \([a,b]\) und einer (stetigen) Funktion \(f\) eine Zahl \(I\) durch die Vorschrift \(I:=\int\limits_a^b f(\xi)\,\mathrm{d}\xi \) definiert. Dieses Vorgehen lässt sich wieder allgemeiner auffassen, indem die obere Integralgrenze als variabel angenommen wird:

Ist \(f\) über jedem abgeschlossenen Teilintervall von \(I\) integrierbar und ist \(a\in I\), so heißt die Funktion\[F_a(x) = \int^{x}_a f(t)\;dt \text{ für alle } x\in I\]
Integralfunktion von \(f\) zur unteren Grenze \(a\).
Die Stammfunktion
An dieser Stelle soll auch der Begriff der Stammfunktion genannt sein.

Definition 2 (Stammfunktion)
Die reellen Funktionen \(f\) und \(F\) seien auf dem Intervall \((a,b)\) definiert. Gilt für jedes \(x\in(a,b)\) die Gleichung \[F'(x) = f(x),\] so heißt \(F\) die Stammfunktion von \(f\) auf dem Intervall \((a,b)\).
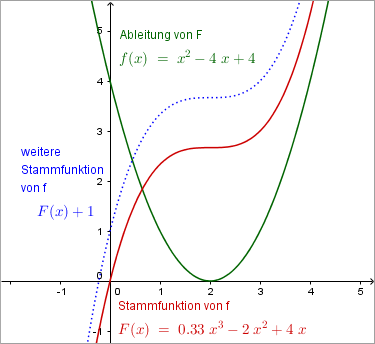
Dabei ist anzumerken, dass es zu jeder Funktion \(f\) unendlich viele Stammfunktionen \(F\) gibt.
Ist \(F\) eine Stammfunktion von \(f\), so sind auch alle durch Addition einer Konstanten erhaltenen Funktionen \(F+c\) Stammfunktionen von \(f\), denn es gilt: \[\frac{d}{dx} (F+c) = \frac{d}{dx} F + \frac{d}{dx} c = f + 0.\]
Umgekehrt unterscheiden sich zwei beliebige Stammfunktionen \(F\) und \(G\) von \(f\) nur durch eine Konstante, d. h. es existiert ein \(c\in\mathbb{R}\), sodass: \(F(x) = G(x) +c.\)
Beispiel 1
Zu \(f(x)=2x\) sind sowohl \(F_0(x) = x^2\) als auch \(F_3 (x) = x^2+3\) oder \(F_{15}(x) = x^2 + 15 \) Stammfunktionen.
Beispiel 2
Die Funktion \(f(x)=e^{x^2}\) ist integrierbar, also für alle \(a\) und \(b\) besitzt das Integral \(\int\limits_a^b e^{\xi^2}\,\mathrm{d}\xi\) einen endlichen Wert. Leider kann aber für die Stammfunktion \(F(x) = \int\limits_a^x e^{\xi^2}\,\mathrm{d}\xi\) keine analytische Darstellung angegeben werden.
Stetige Funktionen besitzen eine Stammfunktion und sind auch integrierbar. Nicht jede riemann-integrierbare Funktion besitzt eine Stammfunktion (z.B: Treppenfunktionen sind integrierbar, können aber keine Stammfunktion besitzen da sie die Zwischenwerteigenschaft nicht erfüllen). Umgekehrt gibt es auch Funktionen, die eine Stammfunktion besitzen, aber nicht riemann-integrierbar sind. Die Existenz einer Stammfunktion ist also nicht äquivalent zur Integrierbarkeit einer Funktion.
Aus der Integrierbarkeit einer Funktion auf einem Intervall folgt die Integrierbarkeit auf Teilintervallen, somit sind für kompakte Intervalle die Integrierbarkeit und die Existenz der Integralfunktion äquivalent.
Der Zusammenhang zwischen Stammfunktion und Integralfunktion wird durch den Hauptsatz der Integral- und Differentialrechnung (HDI) deutlich.

Satz 1 (Hauptsatz der Differential- und Integralrechnung)
- Für \(G(x):=\int\limits_a^x f(\xi)\, \mathrm{d}\xi \) gilt: \[ G'(x) = f(x), \quad x\in(a,b).\]
- Sei \(F\) eine beliebige Stammfunktion der stetigen Funktion \(f\) auf \(D_f\subset\mathbb{R}\), so gilt:
\[I=G(b)=\int\limits_a^b f(\xi)\,\mathrm{d}\xi = [F(\xi)]_a ^b = F(b) - F(a). \]
Beispiel 3
\(\int \limits _0 ^2 f(x)\, \mathrm d x = \int \limits _0 ^2 2x\, \mathrm d x = [x^2-5] _0 ^2 = 2^2 -5-( 0^2-5) = 4\)
(Hierbei wurde als Stammfunktion für \(f(x)=2x\) die Funktion \(x^2-5\) gewählt.)
Dies ist gleichzeitig der Flächeninhalt von \(0\) bis \(2\) unter der Funktion \(2x\).
(Berechnet durch die Dreiecksformel \(\frac{1}{2} \cdot\) Grundlinie \(\cdot\) Höhe \(= \frac{1}{2} \cdot 2 \cdot 4=4\).)
Bemerkung. Die Anwendung des Hauptsatzes funktioniert für jede beliebige Stammfunktion. Stammfunktionen unterscheiden sich nämlich nur durch ein konstantes Glied, das bei der Rechnung verschwindet (wie es im obigen Beispiel mit dem konstanten Glied 5 geschieht).
Neben den bestimmten Integralen der Form \(\int\limits_a^b f(\xi)\,\mathrm{d}\xi\) gibt es auch Integrale der Form \[F(x) = \int f(x)\,\mathrm{d}x.\] Diese Integrale ohne Grenzen heißen unbestimmte Integrale und beschreiben die Menge aller möglichen Stammfunktionen einer Funktion \(f\).

Unbestimmtes Integral
Fehlt im Integral die Angabe von Integrationsgrenzen, so spricht man von einem unbestimmten Integral \(\int f(x)\, \mathrm d x \). Unbestimmte Integrale haben meistens nicht den Zweck, einen bestimmten Flächeninhalt zu berechnen, sondern die Stammfunktion einer Funktion anzugeben.

Ergänzungen zum Hauptsatz der Differential- und Integralrechnung
Bestimmte Integrale können nach dem Hauptsatz mit Hilfe einer beliebigen Stammfunktion berechnet werden.
Der zweite Hauptsatz folgt im Wesentlichen aus dem 1. Hauptsatz, nach dem die Integralfunktion \(F_a\) auch eine Stammfunktion von \(f\) ist, sich also lediglich durch eine additive Konstante \(c\) unterscheidet, d. h. es gilt: \(F(x)=F_a(x)+c\) für alle \(x \in I\).
Einsetzen von \(a\) und \(b\) ergibt:
\(F(a)=F_a(a)+c=c\) und \(F(b)=F_a(b)+c=F_a(b)+F(a)\)
Daraus folgt: \[ \int^{b}_a f(x)\;dx = F_a(b) = F(b) - F(a)\]
Wir hatten die Integralfunktion \(F(x) = \int_a^xf(t)\, \mathrm{d}t\) definiert, wobei \(f\) eine stetige Funktion sei. Es gilt der folgende Satz:

Satz 2 (Differenzierbarkeit der Integralfunktion)
Die Integralfunktion \(F(x)\) ist differenzierbar und es gilt:
\[\frac{d}{dx}F(x) = \frac{d}{dx} \int_a^xf(t)\, \mathrm{d}t = f(x)\]

Bemerkung. Es gibt Funktionen, die integrierbar sind, deren Stammfunktion nicht geschlossen darstellbar ist. So ist die Funktion \[g(x):=e^{-x^2}\] stetig und die Integrale \(\int_a^b e^{-x^2}\,\mathrm{d}x\) existieren, aber es gibt keine geschlossen Darstellung für \(\int e^{-x^2}\,\mathrm{d}x\). Diese Funktion wird auch als Fehlerfunktion bezeichnet
\[\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-r^2}\,\mathrm{d}r.\]

6.4. Technisches Integrieren

Technisches Integrieren
Das Symbol \(\int \limits_a^b f(x)\, \mathrm d x\) wurde bis jetzt verwendet, um den Flächeninhalt unter der Funktion \(f\) zwischen den Punkten \(a\) und \(b\) zu berechnen oder als Rechenoperation.
Doch wie genau wird aus dem Symbol eine Zahl?
Die Antwort darauf gibt der bereits genannte Hauptsatz der Differential- und Integralrechnung. Für jede beliebige Stammfunktion \(F\) zur Funktion \(f\) ist \[\int \limits_a^b f(x)\, \mathrm{d}x = F(b)-F(a).\]
Um ein Integral zu berechnen, sind zwei Schritte nötig:
- Stammfunktion finden: Gesucht ist eine Funktion \(F\), für die gilt \(F'(x)=f(x)\) für alle \(x\in(a,b)\). Wie wir bereits wissen, gibt es für jede Funktion verschiedene Stammfunktionen, die sich alle nur durch addierte Konstanten unterscheiden. Am einfachsten ist es, die Stammfunktion mit der Konstante \(0\) zu verwenden. Bei der Berechnung wird dann gewöhnlich die Stammfunktion in eckige Klammern geschrieben und die Grenzen rechts von der rechten Klammer angefügt: \([F(x)]_{x=a}^{x=b}\).
- Grenzen einsetzen: Nun werden die Werte \(b\) und \(a\) in die Funktion \(F\) eingesetzt und deren Differenz berechnet.
Beispiel 4
Berechne \(\int_{-1}^{1} e^{-x}\, \mathrm{d} x\).
Die Stammfunktion von \(e^{-x}\) ist \(-e^{-x}\), denn es gilt: \((-e^{-x})'=-e^{-x}\cdot(-1) = e^{-x}\). Also gilt:
\[\int_{-1}^{1} e^{-x}\, \mathrm{d} x=\left[-e^{-x}\right]_{x=-1}^{x=1}=-e^{-1}-(-e^{1})=-e^{-1}+e^{1}=2\cdot\sinh(1).\]
Beispiel 5
Berechne \(\int\limits_{0}^{1} \sin(\pi x)\, \mathrm{d} x\).
Die Stammfunktion von \(\sin(\pi x)\) ist \(-\frac1{\pi}\cos(\pi x)\), denn es gilt:
\((-\frac1{\pi}\cos(\pi x))'=-\frac1{\pi}\left(-\sin(\pi x)\cdot \pi\right) = \sin(\pi x)\). Also gilt:
\[\int\limits_{0}^{1} \sin(\pi x)\, \mathrm{d} x =\left[-\frac1{\pi}\cos(\pi x)\right]_{x=0}^{x=1}= -\frac1{\pi}\left(\cos(\pi)-\cos(0)\right) = -\frac2{\pi}.\]
Weiterführendes Beispiel
Gesucht ist das Integral \(\int\limits_0^1 \frac{x}{\sqrt{25-9x^2}}\mathrm{d} x\).
Die Stammfunktion lässt sich mit folgendem Ansatz finden: Wir betrachten \(F(x) = a(25-9x^2)^{\frac 12}\), wobei \(a\) eine reelle Zahl sei. Es gilt:
\[ \frac{\mathrm{d}}{\mathrm{d}x} F(x) = \frac{\mathrm{d}}{\mathrm{d}x}\left(a(25-9x^2)^{\frac 12}\right) = a\cdot \frac12 \cdot (25-9x^2)^{-\frac 12}\cdot 2\cdot 9 x = \frac{9 a x}{(25-9x^2)^{\frac 12}}.\]
Für \(a = \frac19\) haben wir die Stammfunktion zum Integranden gefunden. Damit erhalten wir
\[\int\limits_0^1 \frac{x}{\sqrt{25-9x^2}}\,\mathrm{d} x= \left[-\frac19 (25-9x^2)^{\frac12} \right]_{x=0}^{x=1}= -\frac19(\sqrt{16}-\sqrt{25})=\frac19 .\]

6.5. Integrale elementarer Funktionen

In diesem Kapitel werden Integrale einiger elementarer Funktionen berechnet.

Konstante Funktionen
Gegeben sei die konstante Funktion \(f(x) = c\). Gesucht ist das Integral \(\int\limits_a^b f(x)\,\mathrm{d} x = \int\limits_a^b c \, \mathrm{d}x\).
- Lösung durch Finden einer Stammfunktion Aus dem vorherigen Kapitel ist bekannt, dass für \(g(x) = c\cdot x\) gilt: \(g'(x) = c\). Das heißt, \(c \cdot x\) ist eine Stammfunktion für \(c\). Damit gilt also:\[\int\limits_a^b c \, \mathrm{d}x =[c \cdot x]_{x=a}^{x=b} = c\cdot b - c \cdot a = c \cdot (b-a).\]
Anmerkung: Natürlich wäre auch eine Funktion \(h(x) = c \cdot x + d\) eine Stammfunktion von \(f\), da die Konstante \(d\in\mathbb{R}\) beim Ableiten wegfällt. Der Einfachheit halber kann also mit \(c \cdot x\) gerechnet werden, da das \(d\) beim Rechnen ohnehin wegfallen würde.
- Lösung durch geometrische Betrachtung Der gesuchte Flächeninhalt unter der konstanten Funktion bildet ein Rechteck mit der Höhe \(c\) und der Länge \(b-a\). Damit ist der Flächeninhalt \(c \cdot (b-a)\), was mit der Lösung des Integrals übereinstimmt.

Lineare Funktionen
Gegeben sei die lineare Funktion \( f(x) = mx\). Gesucht ist das Integral \(\int\limits_a^b f(x)\, \mathrm dx\).
- Lösen durch Finden einer Stammfunktion Die Stammfunktion einer linearen Funktion ist auf jeden Fall eine quadratische Funktion, da \(\frac{\mathrm d}{\mathrm dx} x^2 = 2x \) gilt, also die Ableitung einer quadratischen Funktion eine lineare Funktion ergibt. Hier ist es noch wichtig, den Vorfaktor zu beachten. Es gilt \(\frac{\mathrm d (m \cdot \frac{1}{2} \cdot x^2)}{\mathrm dx} = mx\).
Damit gilt für das Integral \(\int\limits_a^b mx \mathrm{d}x = \left[\frac{m}{2}x^2 \right]_{x=a}^{x=b}= \frac{m}{2}b^2 - \frac{m}{2}a^2 \).
- Lösen durch geometrische Betrachtung Das gesuchte Integral ergibt sich geometrisch, indem vom Flächeninhalt des Dreiecks mit den Ecken \((0|0)\), \((b|0)\) und \((b| mb)\) der des Dreiecks mit den Ecken \((0|0)\), \((a|0)\) und \((a| ma)\) abgezogen wird. Aus Formel für den Flächeninhalt von Dreiecken \(\frac{1}{2} \cdot \mbox{Grundlinie} \cdot \mbox{Höhe}\) folgt, ist der Flächeninhalt des ersten Dreiecks \(\frac{1}{2}\cdot b \cdot mb = \frac{1}{2}mb^2\) und der des zweiten Dreiecks analog \(\frac{1}{2}ma^2\). Für das Integral ergibt sich somit \(\frac{m}{2}b^2 - \frac{m}{2}a^2\). Dies stimmt mit dem Integral, das mit Hilfe der Stammfunktion berechnet wurde, überein.

Potenzfunktionen
Gesucht ist das Integral \(\int\limits_a^b x^n\, \mathrm dx\). Bei konstanten und linearen Funktionen haben wir schon gesehen, dass der Exponent einer Funktion beim Ableiten um Eins kleiner wird. Beim Integrieren muss er also größer werden. Es gilt:
\[\frac{\mathrm d }{\mathrm dx}x^n = n \cdot x^{n-1}. \]
Das heißt, die Stammfunktion für \(x^n\) muss den Exponenten \(n+1\) besitzen. Es gilt:
\[\frac{\mathrm d }{\mathrm dx} x^{n+1}= (n+1) \cdot x^n\].
Somit muss die Gleichung noch mit \(\frac{1}{n+1}\) multipliziert werden, damit sich der Faktor vor dem \(x^n\) wegkürzt:
\[\frac{\mathrm d}{\mathrm dx} \frac{1}{n+1} x^{n+1} = \frac{n+1}{n+1} \cdot x^n = x^n\].
Es gilt also: \(\int x^n\, \mathrm dx = \frac{1}{n+1} x ^{n+1},\,c\in\mathbb{R}\).
Beispiele
- \(\int x^2\, \mathrm dx = \frac{1}{3} x^3 +c,\,c\in\mathbb{R}\)
- \(\int x^3\, \mathrm dx = \frac{1}{4} x^4 +c,\,c\in\mathbb{R}\)
- \(\int x^{20}\, \mathrm dx = \frac{1}{21} x^{21} +c,\,c\in\mathbb{R}\)
Die Formel \(\int x^n\, \mathrm dx = [\frac{1}{n+1} x^{n+1}] \) lässt sich auch anwenden, falls der Exponent der Funktion keine natürliche Zahl und nicht \(-1\) ist.
Beispiele
- \(\int x^{2,7}\, \mathrm dx = \frac{1}{3,7} x^{3,7}+c,\,c\in\mathbb{R}\)
- \(\int \sqrt{x}\, \mathrm dx = \int x^\frac{1}{2} = \frac{2}{3} x^{\frac{3}{2}}+c,\,c\in\mathbb{R}\)
- Aber: Für \(x>0\) gilt\(\int x^{-1}\,\mathrm d x=\ln(x)+c,\,c\in\mathbb{R}.\)

Aufgabe Überlegen Sie sich, dass für \(x<0\) die Formel \(\int x^{-1}\,\mathrm d x=\ln(-x)+c,\,c\in\mathbb{R}\) gilt.

Natürliche Exponentialfunktion
Die natürliche Exponentialfunktion \(f(x) = e^x\) ist eine der am einfachsten zu differenzierenden und zu integrierenden Funktionen.
Da die Ableitung von \(e^x\) auch wieder \(e^x\) ergibt, ist \(\int e^x\, \mathrm dx = e^x +c, \, c\in \mathbb{R}\).
Beispiel 1
Bestimme den Wert des Integrals \(\int_0^1 e^z \,\mathrm{d} z\).
\[\int\limits_0^1e^z\,\mathrm{d}z= \left[e^z\right]_{z=0}^{z=1}=e^1-e^0=e-1.\]
Beispiel 2
Bestimme den Wert des Integrals \(\int_0^b e^{\alpha t} \,\mathrm{d} t\).
\[\int\limits_0^b e^{\alpha t}\,\mathrm{d}t=\left[ \frac{1}{\alpha}e^{\alpha t}\right]_{t=0}^{t=b}=\frac{1}{\alpha}\left(e^{\alpha b}-e^0\right)=\frac{1}{\alpha}\left(e^{\alpha b}-1\right).\]

Natürliche Logarithmusfunktion
Die Ableitung der natürlichen Logarithmusfunktion ist \(\ln'(x) =\frac{1}{x}\) für \(x>0\). Es gilt sogar \(\ln'(x) =\frac{1}{x}\) für \(x<0\). Diese Ergebnisse zusammen ergeben für die Stammfunktion von \(\frac{1}{x}\)
\[\int \frac{1}{x}\,\mathrm{d}x = \ln\left(|x|\right) +c , c\in\mathbb{R}.\]
Für den natürlichen Logarithmus kann eine Stammfunktion angegeben werden:
\[ x\ln(x) - x + c ,\, c\in\mathbb{R}.\]
Überzeugen Sie sich durch Differentiation von der Gültigkeit dieser Gleichung.
Beispiel 3
Bestimme den Wert des Integrals \(\int_{\frac12}^e \ln(x)\,\mathrm{d} x\). Es gilt:
\[\int_{\frac12}^e \ln(x)\,\mathrm{d} x = \left[x\ln(x) - x\right]_{x=\frac12}^{x=e} = \left[\left[e\ln(e) - e\right]-\left[\frac12\ln\left(\frac12\right) - \frac12\right]\right]=\frac12\left(1+\ln(2)\right).\]

Trigonometrische Funktion
Auch die Stammfunktionen von \(\sin\) und \(\cos\) ergeben sich logisch, wenn man "rückwärts" ableitet.
\(\int \sin(x)\, \mathrm dx = -\cos(x)+c,\,c\in\mathbb{R}\), da \( (-\cos(x))' =-(-\sin(x))=\sin(x)\)
\(\int \cos(x)\, \mathrm dx = \sin(x)+c,\,c\in\mathbb{R}\), da \((\sin(x))' = \cos(x) \) gilt.
Beispiel 4
Welche Fläche schließt der Sinus im Intervall \([0,\pi]\) mit der \(x\)-Achse ein?
Zur Bestimmung des Flächeninhaltes können wir einfach das bestimmte Integral \(\int_0^{\pi} \sin(\tau) \, \mathrm{\tau}\) bestimmen:
\[\int_0^{\pi} \sin(\tau) \, \mathrm{d}\tau = \left[-\cos(\tau)\right]_{\tau=0}^{\tau=\pi} = -\cos(\pi) - (-\cos(0)) = -(-1) - (-1) = 2.\]
Beispiel 5
Wie lautet das unbestimmte Integral \(\int \cos(\omega t +\phi)\,\mathrm{d}t\)?
Zur Bestimmung des Integrals können wir die Stammfunktion des Kosinus verwenden: \(\sin'(x) = \cos(x)\). Allerdings muss in der gegebenen Funktion noch die innere Ableitung berücksichtig werden. Damit erhalten wir \(\int \ \cos(\omega t +\phi)\,\mathrm{d}t =\frac{1}{\omega}\sin(\omega t+\phi).\)

6.6. Integrationsregeln

Im letzten Kapitel haben wir gesehen, dass die Stammfunktion ein Hilfsmittel ist, um Integrale zu berechnen und dass es für einige Funktionen relativ leicht ist, diese zu bestimmen. Für komplexe Funktionen, z.B. \(\cos(x)e^{\sin(x)^2}\) ist das komplizierter. In diesem Kapitel werden Techniken gezeigt, mit denen trotzdem noch eine "Integration per Hand" funktioniert.
Die meisten Funktionen sind Kombinationen aus verschiedenen elementaren Funktionen. Diese Kombinationen können zum Beispiel durch Addition, Multiplikation oder Verkettung von Funktionen entstehen. Wie beim Differenzieren gibt es auch beim Integrieren Regeln, um diese Kombinationen aufzulösen und komplizierte zusammengesetzte Funktionen auf einfachere Darstellungen zurückzuführen. Die Regeln für die Integration lassen sich aus den Regeln fürs Ableiten herleiten.
Im Hauptsatz der Differential- und Integralrechnung wird die Stammfunktion \(F\) für stetige Funktionen \(f\) eingeführt. Es gilt dann \(F(x)'=f(x),\, x\in D_f\). Für stückweise stetige Funktionen \(g\) mit \(D_g\subset\mathbb{R}\) lässt sich mit Hilfe einer Integralfunktion eine verallgemeinerte Stammfunktion definieren.
Definition 1 (verallgemeinerte Stammfunktion)
Es wird
\[G(x) := \int_a^x g(\xi)\,\mathrm{d} \xi\]
gesetzt, wobei \(a\in D_g\) gilt. \(G\) ist dann eine stetige Funktion auf \(D_g\) und auf den Definitionsabschnitten von \(g\) stimmt \(G'\) mit \(g\) überein.
Frage: Überlegen Sie sich, warum \(G\) stetig sein muss, insbesondere an den Punkten, in denen die Definitionsabschnitte zusammentreffen. Ein möglicher Weg nutzt den Mittelwertsatz der Integralrechnung.
Beim Ableiten gibt es für Brüche eine schöne Regel (Quotientenregel). Bei der Integration ist dies jedoch nicht so einfach. Hier ist es zunächst nur möglich, für einige Spezialfälle Regeln anzugeben.
Beispiele
Stückweise definierte Funktion
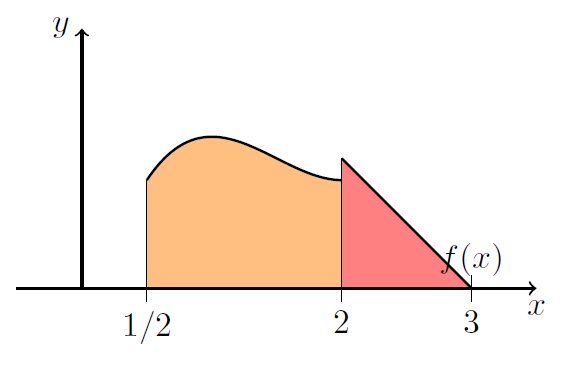

Logarithmische Integration
Bekanntlich ist die Ableitung des \(\ln\) an einer Stelle \(x>0\), also des natürlichen Logarithmus zur Basis \(e\), gleich \(\frac{1}{x}\). Nach der Kettenregel für die Ableitung gilt außerdem für eine differenzierbare positive Funktion \(f\,:\,\frac{\mathrm d}{\mathrm dx} \ln (f(x)) = \frac{f'(x)}{f(x)}\).
Das heißt, für Brüche, bei denen der Zähler gleich der Ableitung des Nenners ist, ergibt sich die Regel
\begin{equation} \int \frac{f'(x)}{f(x)}\, \mathrm{d} x= \ln \left(|f(x)|\right) +c,\,c\in\mathbb{R}.\end{equation}
Die Betragsstriche sind wichtig, da in den Logarithmus nur positive Werte eingesetzt werden können.

Partialbruchzerlegung
Die logarithmische Integration funktioniert gut bei Spezialfällen von gebrochen rationalen Funktionen, bei denen der Zähler ein Vielfaches der Ableitung des Nenners ist. Andere Fälle lassen sich aber manchmal auf diesen zurückführen. Dieses Verfahren hießt Partialbruchzerlegung, mit der gebrochen rationale Funktionen als Summe mehrerer gebrochen rationaler Funktionen darstellt werden können.

Partielle Integration
Für Ableitung eines Produkts zweier einmal stetig differenzierbarer Funktionen \(f\) und \(g\) gilt:
\[(f(x)\cdot g(x))' = f'(x)\cdot g(x)+f(x)\cdot g'(x),\quad x\in(a,b).\]
Dieses Vorgehen wird nun genauer beschrieben.
Satz 1 (Partielle Integration)
\(f : [a,b] \to \mathbb R\) und \(g : [a,b] \to \mathbb R\) seien auf dem Intervall \([a,b]\) differenzierbar und die Ableitungen \(f^{\prime}\) und \(g^{\prime}\) auf \([a,b]\) seien stetig. Dann gilt
\[\int\limits^b_a f^{\prime}(x)g(x)\,\mathrm d{x} = f (x) g (x) \Bigl|^b_a - \int\limits^b_a f (x) g^{\prime} (x)\,\mathrm d{x}\]

Substitution
Satz 2 (Substitution)
\(f\) sei auf \([a,b]\) stetig und \(g\) auf \((a,b)\) stetig differenzierbar. Dann gilt
\[\int_a^bf(g(x))g'(x)\, dx = \int_{A}^{B} f(u)\, \mathrm du,\]
mit \(A=g(a),\ B=g(b)\)

6.7. Anwendungen

In diesem Kapitel stellen wir Beispiele vor, bei denen die Integration ein wesentlicher Bestandteil der Berechnung ist.

Beispiel 1 (Beschleunigung)
Die Ableitung einer Strecke \(s=s(t)\) nach der Zeit ergibt die Geschwindigkeit: \(v(t)=\frac{\mathrm{d}}{\mathrm{d}t}s(t)\). Die Ableitung der Geschwindigkeit wiederum ergibt die Beschleunigung: \(a(t)=\frac{\mathrm{d}}{\mathrm{d}t}v(t)=\frac{\mathrm{d^2}}{\mathrm{d}t^2}s(t)\).
Umgekehrt bedeutet das, dass sich Geschwindigkeit und Weg durch ein- bzw. zweimalige Integration der Beschleunigung ergeben:
\[v = \int a(t)\, \mathrm d t, \quad s = \int v(t)\, \mathrm d t\].
Durch die unten angegebenen Rechnungen ergeben sich die aus der Physik bekannten Formeln für Geschwindigkeit und Weg in Abhängigkeit von einer konstanten Beschleunigung. Konstante Beschleunigung bedeutet, dass die Funktion für die Beschleunigung konstant ist, d.h. \(a(t)\equiv \mbox{const}\). Im Folgenden wird also mit der Konstanten \(a\) gerechnet.
Für die Geschwindigkeit gilt:
\[v = \int a \mathrm d t = at + C_1 \].
Die Integrationskonstante wird dabei aus dem Anfangswert \(v(0) = v_0\) berechnet, es folgt
\[v(t) = a\cdot t + v_0\].
Für den Weg ergibt sich damit:
\begin{equation} s(t) = \int v(t)\, \mathrm d t = \int (a\cdot t + v_0)\, \mathrm d t = \frac{1}{2} a\cdot t^2 + v_0\cdot t + C_2.\end{equation}
In diesem Fall ist die Integrationskonstante der Anfangsort \(s(0) = s_0\) und somit gilt:
\[s(t) = \frac{1}{2} a\cdot t^2 + v_0 \cdot t + s_0.\]

Beispiel 2 (Effektivwert)
Die momentane Spannung in einem Wechselstromkeis sei durch
\[u(t) = u_m \cos(\omega t) \]
und die momentane Stromstärke sei durch \[i(t)= i_m \cos(\omega t + \phi).\]
Die momentane Leistung beim Wechselstrom ist gegeben durch
\[u(t)i(t) = u_m \cos(\omega t) \cdot i_m \cos(\omega t + \phi).\]
Die Wirkleistung ist definiert als
\[\bar{P_0} = \frac1T \int_0^T u(t)i(t)\mathrm d t = \frac1T \int_0^T u_m \cos(\omega t) \cdot i_m \cos(\omega t + \phi)\mathrm d t.\]
Es ist also das Integral \( \int_0^T u_m \cos(\omega t) \cdot i_m \cos(\omega t + \phi)\mathrm d t\) zu berechnen. Hierbei helfen uns die Addtionstheoreme:
\[2\cos\left(\frac{x+y}2\right) \cdot \cos\left(\frac{x-y}2\right) = \cos(x) + \cos(y).\]
Aus \( \frac{x+y}2=\omega t + \phi\) und \( \frac{x-y}2=\omega t\) erhalten wir
\[x=2\omega t + \phi \qquad \mbox{und} \qquad y = \phi t\]
Damit erhalten wir
\[u(t)i(t) = \frac{u_m \cdot i_m}{2}\left(\cos(\phi) + \cos(2\omega t + \phi)\right).\]
Mit \(U = \frac{u_m}{\sqrt{2}}\) und \(I = \frac{i_m}{\sqrt{2}}\)
\begin{eqnarray} \bar{P_0} & = & \frac{U\cdot I}T \int_0^T \cos(\phi) + \cos(2\omega t + \phi)\mathrm d t\\& = & U I \cos(\phi) \end{eqnarray}
Dieses Beispiel orientiert sich an dem Beispiel von Burg, Haf, Wille: Höhere Mathematik für Ingenieure, Band I: Analysis, 8. Auflage, Teubner Verlag 2008, Kapitel 4.4, S. 349

Beispiel 3 (Wasserdruck auf eine Seitenwand)
Wir betrachten ein Wasserbecken mit einer Seitenwand in Form einer Ellipse. Die Wand kann durch \[\frac{x^2}{a^2}+\frac{y^2}{b^2}-1=0\]
beschrieben werden. Wir stellen uns vor, dass diese Seitenwand in infinitesimal schmale Streifen der Höhe \(\mathrm{d}y\) und der Breite \(2x\) geschnitten wurde. Der Flächeninhalt eines Streifens ist dann \[\mathrm{d}f = 2x\,\mathrm{dy}.\]
Der Wasserdruck \(\mathrm{d}P\) auf diesem Streifen hängt von der Höhe des Wassers darüber ab; das Wasser gehe bis zur \(x\)-Achse. Damit ist der Druck gegeben durch
\[\mathrm{d}P = 2x\mathrm{d}y \cdot y \cdot \gamma.\]
Um den Gesamtdruck \(P\), der auf die Seitenwand wirkt, zu berechnen, müssen wir über die gesamte Wasserhöhe integrieren. Das heist also \[P = \int_{y=0}^{y=b} 2x \cdot y \cdot \gamma\, \mathrm{d}y.\]
Nun hängt der Integrand aber von \(x\) ab. \(x\) können wir aber durch \(y\) ausdrücken, denn es gilt:
\[ x = a\sqrt{1-\frac{y^2}{b^2}}=\frac{a}{b}\sqrt{b^2-y^2}.\]
Dies führt nun auf \[P = \int_{y=0}^{y=b} 2x \cdot y \cdot \gamma\, \mathrm{d}y=\int_{y=0}^{y=b} 2\frac{a}{b}\sqrt{b^2-y^2} \cdot y \cdot \gamma \,\mathrm{d}y.\]
Das Integral kann nun mit Hilfe der Substitution \(z = b^2-y^2\) und \(\mathrm{d}z = -2y\mathrm{d}y\) gelöst werden. An den Rändern müssen wir aber bei der Substitution aufpassen: \(z(0) = b^2\) and \(z(b) = 0\).
Mit diesen Überlegungen erhalten wir nun:
\begin{eqnarray} P & = & \int_{y=0}^{y=b} 2\frac{a}{b}\sqrt{b^2-y^2} \cdot y \cdot \gamma\, \mathrm{d}y\\& = & \gamma\int_{z=b^2}^{z=0} -\frac{a}{b}\sqrt{z} \mathrm{d}z \\ & = & \gamma\frac{a}{b} \left[-\frac23z^{\frac32}\right]_{z=b^2}^{z=0}\\& = & \gamma\frac{a}{b} \left[-0+\frac23(b^2)^{\frac32}\right]=\frac23 \gamma a b^2.\end{eqnarray}.
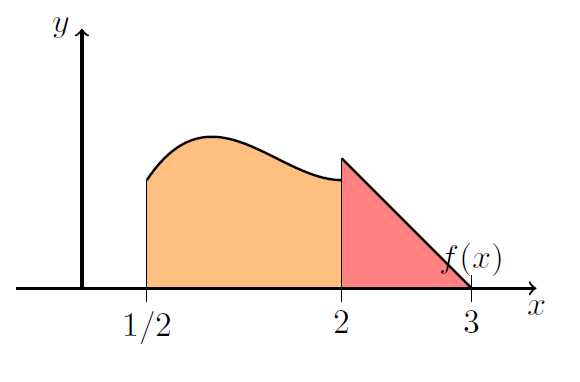

Geometrische Anwendungen
Beispiel 4 (Flächeninhalte)
Die bekannteste Anwendung ist die Interpretation des Integrals als Fläche zwischen einer Funktion und der \(x\)-Achse.
Der Flächeninhalt ist gegeben durch \(A = \int_a^b |f(x)|\,\mathrm{d}x\). Im Bild ist die \(f(x) = -\sin(x)+\frac1{\sqrt{2}}\) dargestellt und der Flächeninhalt kann berechnet werden durch
\[A = \int_0^{2\pi} |f(x)|\,\mathrm{d}x = \int_{0}^{\frac{\pi}4}-\sin(x)+\frac1{\sqrt{2}}\,\mathrm{d}x +\]
\[+\int_{\frac{\pi}4}^{\frac{3}4\pi}\sin(x)-\frac1{\sqrt{2}}\,\mathrm{d}x\int_{\frac{3}4\pi}^{2\pi}-\sin(x)+\frac1{\sqrt{2}}\,\mathrm{d}x=\sqrt{2}\pi.\]

Beispiel 5 (Länge eines Funktionsgraphen)
Die zugrundeliegende Idee ist ganz interessant. Ein infinitesimal kleines Stück des Graphen besitzt die Länge\[\Delta s \approx \sqrt{(\Delta x)^2+(\Delta y)^2}=\sqrt{1+\left(\frac{\Delta y}{\Delta x}\right)^2}\Delta x\approx \sqrt{1+f'(x)^2}\Delta x.\]
Wenn wir nun über das Intervall \((a,b)\) integrieren, erhalten wir
\[l = \int_a^b \sqrt{1+f'(x)^2} \,\mathrm{d}x.\]
Damit erhalten wir für die Länge des Graphen der Funktion \(g(x) = \cosh(x)\) über \([-1,1]\)
\[ l = \int_{-1}^{1} \sqrt{1+\sinh(x)^2} \,\mathrm{d}x = \int_{-1}^{1} \cosh(x) \,\mathrm{d}x = 2\sinh(1).\]
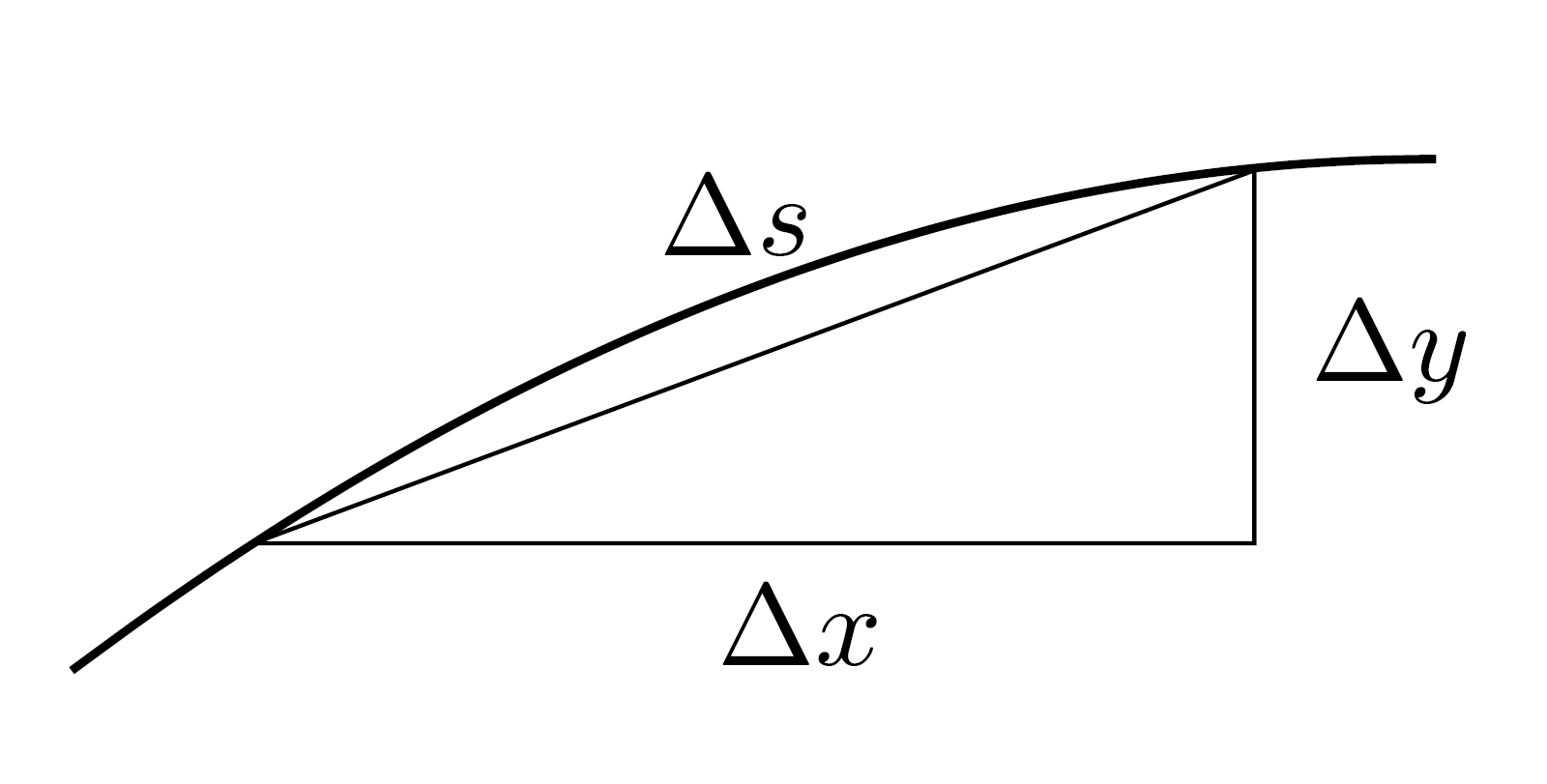
Beispiel 6 (Flächeninhalt einer Rotationsfläche)
Wieder betrachten wir eine Funktion \(y=f(x)\) auf dem Intervall \([a,b]\). Diesmal wird die Funktion um die \(x\)-Achse rotiert, d.h. die Funktion \(f(x) = \cosh(x)\) auf \([-1,1]\).
Für ein beliebiges \(x\) aus diesem Interval sehen wir infinitesimal dünne Kreise mit der Bogenlänge \(2\pi |f(x)|\) und der Breite \(\sqrt{1+f'(x)^2}\Delta x\). Auf diese Weise erhalten wir den Flächeninhalt dieses Kreises
\[2\pi |f(x)|\cdot\sqrt{1+f'(x)^2}\Delta x.\]
Durch Integration über das Intervall \([a,b]\) erhalten wir den Flächeninhalt
\[A = 2\pi\int_a^b |f(x)|\cdot\sqrt{1+f'(x)^2}\,\mathrm{d}x. \]
In unserem Beispiel erhalten wir
\[ A = 2\pi \int_{-1}^{1} \cosh(x)\sqrt{1+\sinh(x)^2}\,\mathrm{x} = 2\pi \int_{-1}^{1} \cosh(x)^2\,\mathrm{x}=2 \pi (1 + \sinh(1) \cosh(1)).\]
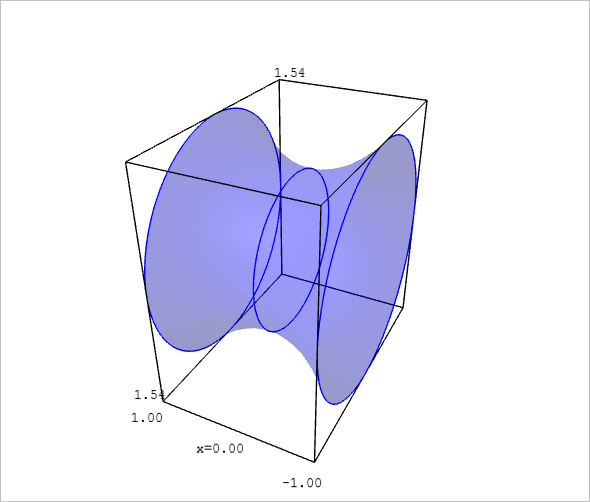
Beispiel 7 (Volumen eines Rotationskörpers)
Wir erweitern nochmal die Idee von oben. An jedem Punkt \(x\) überdeckt der Kreis die Fläche \(A(x) = \pi f(x)^2\). Durch Integration von \(a\) nach \(b\) erhalten wir das Volumen \[ V = \int_a^b A(x) \,\mathrm{d} x = \pi \int_a^b f(x)^2\,\mathrm{d} x.\]
In unserem Beispiel führt dies auf folgendes:
\[ V = \int_{-1}^{1} A(x) \,\mathrm{d} x = \pi \int_{-1}^{1} f(x)^2\,\mathrm{d} x =\pi \int_{-1}^{1} \cosh(x)^2\,\mathrm{d} x = \pi (1 + \sinh(1) \cosh(1)).\]

6.8. Aufgaben


Aufgaben zum 6. Kapitel "Integration".
Aufgabe 1.
Gegeben seien die Funktion \(f(z):=\cos(2\pi z)+1 \) und die Zerlegung des Intervalls \( [0,1]\): \(Z=\{0,\frac{1}{8},\frac{1}{4},\frac{3}{8},\frac{1}{2},\frac{5}{8},\frac{3}{4},\frac{7}{8},1\}\).Aufgabe 2.
Welche der folgenden Funktionen sind auf\([-1,1]\) integrierbar:
\(g_1(x):=x^n, n\in\mathbb{N}, \)
\(g_2(z):=\frac1z, z\ne0, \)
\(g_3(t):=\cot(t),t\ne0 \)
\(g_4(y):=\tan(y). \)
Aufgabe 3.
Gegeben sei die Funktion \( h(\varphi):=\varphi^2-\varphi-1 \)
Bestimmen Sie einen Punkt \(\overline{\varphi}\in \left[0,1\right] \) , so dass die Gleichung \(h(\overline{\varphi})\cdot(1-0)=\int\limits_{0}^{1} \xi^2-\xi-1\,\mathrm{d}\xi \) erfüllt ist.
Aufgabe 4.
Bestimmen Sie folgende Integrale:
1. \( \int\limits_{{0}}^{{2}} {-3\cdot e^{3\cdot t}\,\mathrm{d}t}\)
2. \( \int\limits_{{-1}}^{{2}} {-2\cdot z^2+2\cdot z+4}\,\mathrm{d}z \)
3. \( \int\limits_{{-2}}^{{\frac{3}{2}}} {\cos \left( \frac{5\cdot \pi\cdot u}{2} \right)}\,\mathrm{d}u \)
4. \(\int\limits_{{1}}^{{5}} \ln(x)\,\mathrm{d}x\)
Aufgabe 5.
Bestimmen Sie folgende Integrale:
1. \( \displaystyle \int {x^2\cdot \sin \left( x \right)} \, \mathrm{d}{x},\)
2. \( {\displaystyle\int 4\cdot e^{2\cdot u}-2\cdot e^{3\cdot u}}\, \mathrm{d}{u} \)
3. \( {\displaystyle \int}{\frac{1}{\sin ^2\left(\pi\cdot u\right)}}\,\mathrm{d}u \)
4. \( \displaystyle\int {\frac{2\cdot \cos \left( 2\cdot z \right)}{\sin \left( 2\cdot z \right)}}\mathrm{d}z \)
Aufgabe 6.
Bestimmen Sie folgendes Integral \( \int {-\frac{x+1}{x^2-2\cdot x+1}} \, \mathrm{d}{x}.\)
Aufgabe 7.
Gegeben sei das Integral \(\int (a+bz)^n\,\mathrm{d}z \) Welche Ausdrücke sind dazu äquivalent:
1. \({\displaystyle \int} \sum\limits_{k=0}^n \begin{pmatrix} n\\k\end{pmatrix} a^kb^{n-k}z^{n-k}\,\mathrm{d}z \)
2. \({\displaystyle \int} a^n+(bz)^n\,\mathrm{d}z\)
3. \({\displaystyle \int} \sum\limits_{k=0}^n \begin{pmatrix} n\\k\end{pmatrix} a^kb^{n-k}z^{n-k}\,\mathrm{d}z \)
4. \(\sum \limits_{k=0}^n\begin{pmatrix} n\\k\end{pmatrix} a^{n-k}b^{k}\int z^{k}\,\mathrm{d}z \)
Aufgabe 8.
Gegeben sei die Funktion \(f(x):=\frac{1}1{\cos^2(z)}.\) Welche der folgende Funktionen sind Stammfunktionen von \(f\)
\( F_1(x)=\frac{\sin(x)}{\cos(x)}+\pi \)
\(F_2(x)=\frac{1}{\pi}\frac{\sin(\pi x)}{\cos(x)}+c,\,c\in\mathbb{R}\)
\(F_3(x) = \frac{1}{\cos(x)}+c,\,c\in\mathbb{R}\)
\(F_4(x) = \tan(x)+c,\,c\in\mathbb{R}\)
Aufgabe 9.
Gegeben sei die Funktion \(r(x):= {\frac{x+11}{x^2+x-12}} \) Welche der folgenden Aussagen sind richtig:
\(\int r(x)\,\mathrm{d}x = \ln(|x^2+x-12|)+c,c\in\mathbb{R}, \)
\(\int r(x)\,\mathrm{d}x = -\ln(|x+4|)+2\ln(|x-3|)+c,c\in\mathbb{R}, \)
\(\int r(x)\,\mathrm{d}x = \ln\left(\left|\frac{x-3}{x+4}\right|\right)+\ln(|x-3|)+c,c\in\mathbb{R},\)
\(\int \limits_{-3}^{4} |r(x)| \infty\,\mathrm{d}x \)

7. Gewöhnliche Differentialgleichungen


In diesem Kapitel werden Methoden zur Lösung der wichtigsten Fälle von Gleichungen 1. und 2. Ordnung vermittelt:
- trennbare und lineare Gleichungen 1. Ordnung
- lineare Gleichungen 2. Ordnung mit konstanten Koeffizienten
- charakteristische Polynome
- homogene und inhomogene Fälle
grundlegende Anwendungen, z.B. exponentieller Zerfall und harmonische Schwingung. Die meisten grundlegenden Typen gewöhnlicher Differentialgleichungen werden zusammen mit elementaren Lösungstechniken behandelt. Es werden mehrere anwendungsorientierte Beispiele behandelt, die sich aus klassischen Problemen der Naturwissenschaften ergeben.
Das Kapitel umfasst:
- Grundlagen zu Differentialgleichungen
- Lösen einer ODE 1. Ordnung
- ODEs 2. und höherer Ordnung
- Übungen

7.1. Begriffe

Eine Differentialgleichung ist eine Gleichung, die eine unbekannte Funktion enthält, z. B. \( y = y(x) \) und ihre Ableitungen \( y'(x), y''(x), \ldots, y^{(n)}(x) \). Diese Art von Gleichung bei der die unbekannte Funktion von einer Variablen abhängt heißt gewöhnliche Differentialgleichung oder einfach nur Differentialgleichung. Wenn die Funktion mehrere Variablen enthält, heißt sie partielle Differentialgleichung, aber diese werden nicht in diesem Kurs behandelt.
Eine typische Anwendung, die zu einer Differentialgleichung führt, ist der radioaktive Zerfall. Wenn \( y=y(t) \)die Anzahl der radioaktiven Nukleare zum Zeitpunkt \( t \)ist, dann ist innerhalb eines kurzen Zeitintervalls \( \Delta t\) die Veränderung der Anzahl näherungsweise \( \Delta y \approx -k y(t)\cdot \Delta t\), wobei \( k\) eine positive Konstante ist und von der radioaktiven Substanz abhängt. Die Approximation wird besser, wenn \( \Delta t \to 0\), so dass \( y'(t) \approx \Delta y/\Delta t \approx -ky(t) \). Daraus folgt, dass die Differentialgleichung \( y'(t)=-ky(t)\) eine mathematische Modellierung für den radioaktiven Zerfall darstellt. In der Realität ist die Anzahl der Nukleare eine ganze Zahl, also ist die Funktion \( y(t)\) nicht differenzierbar (oder die Ableitung ist meist Null!) Somit beschreibt das Modell die Eigenschaften einer idealisierten, glatten Version von \( y(t)\). Das ist ein typisches Phänomen in den meisten Modellierungen.
Ordnung
Die Ordnung einer Differentialgleichung entspricht der höchsten Ordnung der Ableitungen, die in der Gleichung vorkommen.
Zum Beispiel ist die Ordnung der Differentialgleichung \( y' + 3y = \sin(x)\) gleich 1. Die Ordnung der Differentialgleichung \( y'' + 5y' -6y = e^x \) ist 2.
Hier ist die Variable von der Funktion \(y\) nicht sichtbar; die Gleichung sieht \(y\) als implizit zu bestimmen vor.
Lösungen von Differentialgleichungen
Eine Differentialgleichung der n-ten Ordnung hat folgende Form
\( \begin{equation} \label{dydef} F(x, y(x), y'(x),\ldots , y^{(n)}(x)) = 0 \end{equation} \)
Die Lösung einer gewöhnlichen Differentialgleichung ist eine n-mal differenzierbare Funktion \(y(x)\), welche die obige Gleichung für alle \( x \in I, \) erfüllt, wobei \(I\) ein offenes Intervall auf der reellen Achse ist.
Typischerweise ist die Lösung nicht eindeutig und es kann eine unendliche Anzahl an Lösungen geben. Betrachte die Gleichung \( xy^2 + y' = 0. \) Die Gleichung hat die Lösungen
- \( y_0(x) = 0,\enspace x \in \mathbb{R} \)
- \( y_1(x) = 2/x^2,\enspace x>0 \)
- \( y_2(x) = 2/x^2,\enspace x<0 \)
- \( y_3(x) = 2/(x^2 + 3),\enspace x \in \mathbb{R} \)
Hier sind \( y_1\), \( y_2\) und \( y_3 \) sogenannte partikuläre Lösungen. Die allgemeine Lösung ist \( y(x) = 2/(x^2 + C),\> C \in \mathbb{R}. \) Partikuläre Lösungen können aus der allgemeinen Lösung abgeleitet werden, indem dem Parameter \(c\) ein Wert zugewiesen wird. Lösungen, die nicht aus der allgemeinen Lösung hervorgehen, nennt man spezielle Lösungen.
Differentialgleichungen müssen nicht unbedingt eine Lösung besitzen. Zum Beispiel die Differentialgleichung erster Ordnung \( \sin(y' + y) = 2 \) hat gar keine Lösung. Wenn eine Gleichung erster Ordnung in die Normalform \( y' = f(x,y) \) umgeschrieben werden kann, wobei \(f\) stetig ist, dann existiert eine Lösung.
Anfangswert-Bedingung
Konstanten in der allgemeinen Lösung können einige Werte gegeben werden, wenn die Lösung weitere Eigenschaften erfüllen soll. Wir könnten zum Beispiel verlangen, dass die Lösung gleich \( y_0 \) bei \( x_0 \) ist, indem wir einen Anfangswert festlegen \( y(x_0) = y_0. \) Mit Gleichungen erster Ordnung wird (normalerweise) nur eine Bedingung benötigt, um eine eindeutige Lösung zu erhalten. Bei Gleichungen zweiter Ordnung brauchen wir entsprechend zwei Werte. In diesem Fall ist die Anfangswertbedingung von folgender Form
\( \left\{ \begin{array} yy(x_0) = y_0 \\ y'(x_0) = y_1 \end{array} \right. \)
Im Allgemeinen, benötigen wir also für eine Gleichung n-ter Ordnung n Anfangswerte, um eine eindeutige Lösung zu erhalten. Eine Differentialgleichung und ihre dazugehörigen Anfangswerte werden gemeinsam als Anfangswertproblem bezeichnet.
Beispiel 1
Wir haben oben gesehen, dass die allgemeine Lösung der Gleichung \( xy^2 + y' = 0 \) durch die Gleichung \( y(x) = 2/(x^2 + C)\) gegeben ist. Damit ist die Lösung des Anfangswertproblems
\( \left\{\begin{align} xy^2 + y' = 0 \\ y(0) = 1 \end{align} \right. \)
gleich \( y(x) = 2/(x^2 + 2).\)
In der unteren Graphik sind ein paar Lösungen für die Gleichung \( xy^2 + y' = 0 \) eingezeichnet. Probiere selbst aus wie die Anfangswertbedingung die Lösung beeinflusst. Die Anfangswerte können verändert werden, indem man die Punkte verschiebt. Ist es möglich, dass sich die Lösungskurven schneiden?
Richtungsfeld
Die Differentialgleichung \( y' = f(x,y) \) kann geometrisch interpretiert werden: Wenn die Lösungskurve (d. h. der Graph einer Lösung) durch einen Punkt \( (x_0, y_0) \) geht, dann gilt \( y'(x_0) = f(x_0, y_0) \),d. h. wir können die Steigungen der Tangenten von dieser Kurve finden obwohl wir noch nicht einmal die Lösung selbst kennen. Richtungsfeld oder Steigungsfeld ist ein Vektorfeld \( \vec{i} + f(x_k, y_k)\vec{j} \) beschrieben durch die Punkte \( (x_k, y_k)\). Die Richtung des Feldes liefert ein ziemlich genaues Bild von dem Verhalten der Lösungskurven.
Beispiel 2
Im unteren Bild ist ein Richtungsfeld entsprechend der Differentialgleichung \( y' = x^2 - y^2 \) eingezeichnet.

7.2. Lösen gewöhnlicher Differentialgleichungen erster Ordnung

Ein offenkundiges Problem in der Theorie der Differentialgleichungen ist, dass es eine relativ geringe Anzahl an Lösungsmethoden, die allgemein anwendbar sind, gibt. Auch für recht einfache Differentialgleichungen existiert normalerweise keine allgemeingültige Formel und besonders für Differentialgleichungen höherer Ordnung ist es rar eine analytische Lösung zu finden. Für manche Gleichungen ist es jedoch möglich und hier werden ein paar der häufigsten Fälle vorgestellt.

Gewöhnliche lineare Differentialgleichungen erster Ordnung
Wenn eine Differentialgleichung der Form
\( p_n(x)y^{(n)} + p_{n-1}(x)y^{(n-1)} + \cdots + p_1(x)y' + p_0(x)y = r(x),\)
ist, dann heißt sie lineare Differentialgleichung. Die linke Seite der Gleichung ist eine Linearkombination der Ableitungen mit dem Multiplikator \( p_k(x) \). Somit ist eine gewöhnliche lineare Differentialgleichung von der Form
\( p_1(x)y' + p_0(x)y = r(x). \)
Wenn \( r(x) = 0 \) für alle \(x\) ist, dann nennt man die Gleichung homogen. Andernfalls ist die Gleichung inhomogen.

Satz 1.
Betrachte ein normiertes Anfangswertproblem
\( \left\{\begin{align}y^{(n)} + p_{n-1}(x)y^{(n-1)} + \cdots + p_1(x)y' + p_0(x)y = r(x) \\ y(x_0) = y_0, \: y'(x_0) = y_1, \: \ldots, \: y^{n-1}(x_0) = y_{n-1}. \end{align} \right. \)
Wenn die Funktionen \( p_k\) und \( r\) stetig im Intervall \( (a,b)\), in dem der Anfangswert \(x_0\) liegt, sind, dann besitzt das Anfangswertproblem eine eindeutige Lösung.
Die Forderung bezüglich der Normierung der Gleichung ist entscheidend. Zum Beispiel kann die Gleichung \(x^2y'' - 4xy' + 6y = 0 \) entweder keine oder eine unendliche Anzahl an Lösungen je nach Anfangswert haben: Substitution von \( x=0 \) in der Gleichung ruft automatisch einen Anfangswert von \( y(0)=0\) hervor.

Lösen einer gewöhnlichen linearen Differentialgleichung 1. Ordnung
Eine gewöhnliche lineare Differentialgleichung 1. Ordnung kann mit Hilfe der integrierenden Faktormethode gelöst werden. Die Idee der Methode ist beide Seiten mit der Gleichung \(y' + p(x)y = r(x) \) mit dem integrierenden Faktor \(\displaystyle e^{\int p(x) dx} =e^{P(x)}\) zu multiplizieren, was es erlaubt die Gleichung in die folgende Form zu schreiben
\(\displaystyle y'(x)e^{P(x)} + p(x)e^{P(x)}y(x) = r(x)e^{P(x)} \Leftrightarrow \frac{d}{dx}\left( y(x)e^{P(x)}\right) = r(x)e^{P(x)}. \)
Das Integrieren beider Seiten der Gleichung liefert
\(\displaystyle y(x)e^{P(x)} = \int r(x)e^{P(x)}\, \mathrm{d}x + C \Leftrightarrow y(x)= Ce^{-P(x)} + e^{-P(x)}\int r(x) e^{P(x)}\, \mathrm{d}x. \)
Es ist nicht ratsam sich die Formel an sich einzuprägen, sondern die Idee wie die Gleichung abgeändert werden sollte, um fortfahren zu können, im Hinterkopf zu behalten.
Beispiel 1.
Lösen wir die Differentialgleichung \(\displaystyle y'-y = e^x+1.\) Der zu integrierende Faktor ist \(\displaystyle e^{\int (-1)\, \mathrm{d}x} = e^{-x}\), also multiplizieren wir beide Seiten mit diesem Ausdruck:
\(\displaystyle e^{-x}y'-e^{-x}y = 1+e^{-x}\)
\(\displaystyle \frac{d}{dx}(y(x)e^{-x}) = 1+e^{-x}\)
\(\displaystyle y(x)e^{-x} = \int 1+e^{-x}\, \mathrm{d}x + C = x - e^{-x} + C\)
\(\displaystyle y(x)= e^xx - 1 + Ce^x.\)
Beispiel 2.
Lösen wir das Anfangswertproblem
\( \left\{\begin{align}xy' = x^2 + 3y \\ y(0) = 1 \end{align} \right. \)
Zuerst wollen wir das Problem in normierter Form ausdrücken:
\( \displaystyle y' - \frac{3}{x}y = x. \)
Nun ist der zu integrierende Faktor \(\displaystyle e^{ \int \frac{3}{x} dx } =\displaystyle e^{ -3 \ln \vert x \vert } =\displaystyle e^{ \ln x^{-3} } =\displaystyle \frac{1}{x^3},\> x>0. \) Somit erhalten wir
\(\displaystyle \frac{y'}{x^3} - \frac{3}{x^4}y = \frac{1}{x^2} \)
\(\displaystyle \frac{d}{dx}(\frac{y}{x^3}) = \frac{1}{x^2} \)
\(\displaystyle \frac{y}{x^3} = \int \frac{1}{x^2}\, \mathrm{d}x + C = - \frac{1}{x} + C\)
\(y = Cx^3 - x^2 \)
Wir haben die allgemeine Lösung gefunden. Da \(y(0) = C\cdot 0 - 0 = 0,\) ist, entspricht der Wert der Funktion nicht dem gegebenen Anfangswert und das Problem hat keine Lösung. Der Hauptgrund hierfür ist, dass der Anfangswert für \( x_0=0\) gegeben ist, für den die normierte Form der Gleichung nicht definiert ist. Jede andere Wahl von \( x_0\) führt zu einer eindeutigen Lösung.
Beispiel 3.
Lösen wir die gewöhnliche Differentialgleichung 1. Ordnung \(xy'-2y=2\) mit folgenden Anfangswerten
- \(y(1)=0\)
- \(y(0)=0\).
Aus der Form \(y'-(2/x)y=2/x\) sehen wir, dass die vorliegende Gleichung eine lineare gewöhnliche Differentialgleichung ist. Der zu integrierende Faktor ist
\[ e^{-\int (2/x)\, \mathrm{d}x} = e^{-2\ln |x|} = e^{\ln (1/x^2)} = \frac{1}{x^2}. \]Multiplizieren mit dem zu integrierenden Faktor liefert uns
\[ (1/x^2)y'(x)-(2/x^3)y(x) =\frac{2}{x^3} \Leftrightarrow \frac{d}{dx}\left( \frac{y(x)}{x^2}\right) = \frac{2}{x^3}, \]also ist die allgemeine Lösung der gewöhnlichen Differentialgleichung \(y(x)=x^2 (-1/x^2+C)=Cx^2-1\). Mit dem Anfangswert \(y(1)=0\) folgt, dass \(C=1\), aber der andere Anfangswert \(y(0)=0\) führt zu einem Widerspruch \(-1=0\). Somit ist die Lösung in Teil a) \(y(x)=x^2-1\), aber eine Lösung, die den Anfangswert aus Teil b) erfüllt, existiert nicht: Durch Substitution von \( x=0 \) folgt aus der Gleichung \( y(0)=-1\).

Getrennte Variablen
Eine Differentialgleichung erster Ordnung hat getrennte Variablen, wenn sie in die Form \( y' = f(x)g(y) \) geschrieben werden kann, wobei \(f\) und \(g\) integrierbare Funktionen im betrachteten Definitionsbereich sind. Behandeln wir formal \( y'(x)=dy/dx\) als einen Bruch und multiplizieren mit \( dx\) und teilen mit \( g(y)\), erhalten wir \( \frac{dy}{g(y)}=f(x)\, dx\). Durch Integration der linken Seite in Anbetracht von \( y\) und der rechten Seite in Anbetracht von \( x\), erhalten wir
\(\displaystyle \int \frac{\mathrm{d}y}{g(y)} = \int f(x)\, \mathrm{d}x + C\)
Diese Methode gibt die Lösung der Differentialgleichung in impliziter Form wider, welche wir im Weiteren explizit lösen können für \(y =y(x)\). Die Rechtfertigung für diese formale Betrachtung wird deutlich, indem andere Variablen für die Integrale benutzt werden können.
Beispiel 4.
Lösen wir die Differentialgleichung \(\displaystyle y'+\frac{2}{5}y = 0 \) mit getrennten Variablen. (Wir könnten die Gleichung auch mit der Methode von integrierbaren Faktoren nehmen.)
\(\displaystyle y'+\frac{2}{5}y = 0 \)
\(\displaystyle \frac{dy}{dx} = -\frac{2}{5}y \)
\(\displaystyle \int \frac{1}{y}\, \mathrm{d}y = -\frac{2}{5} \int \, \mathrm{d}x \)
\(\displaystyle \ln |y| = -\frac{2}{5}x + C_1 \)
\( \displaystyle y =\pm e^{-\frac{2}{5}x+C_1} = \pm e^{-\frac{2}{5}x}e^{C_1} = Ce^{-\frac{2}{5}x}, \: C\neq 0. \)
Im letzten Schritt, haben wir aufgrund von Einfachheit \(C =\pm e^{C_1}\) geschrieben. Der Fall \( C=0\) ist auch erlaubt, da es zu trivialen Lösung \(y(x)\equiv 0\) führt, siehe unten.
Beispiel 5.
Lösen wir das Anfangswertproblem
\( \left\{\begin{align}y' = \frac{x}{y} \\ y(0) = 1 \end{align} \right. \)
Da die allgemeine Lösung nicht notwendig ist, können wir eine Abkürzung durch Anwendung des Integrals in folgenderweise nehmen:
\(\displaystyle \frac{dy}{dx} = \frac{x}{y} \)
\(\displaystyle \int_1^y y \, \mathrm{d}y =\int_0^x x \, \mathrm{d}x \)
\(\displaystyle \frac{1}{2}y^2 - \frac{1}{2} =\frac{1}{2}x^2 \)
Die Lösung ist \( y=y(x)=\sqrt{x^2+1}\).

Triviale Lösungen gewöhnlicher Differentialgleichung mit getrennten Variablen
Allgemeinen Lösungen, die durch die Anwendung der Methode für getrennte Variablen gewonnen werden, fehlt es normalerweise an Information an Lösungen bezüglich der Nullstellen der Funktion \(g(y)\). Der Grund hierfür ist, dass wir bei der Methode für getrennte Variablen voraussetzen müssen, dass \(g(y(x)) \neq 0\) gilt, um den Ausdruck durch \(g(y(x))\) dividieren zu können. Es fällt auf, dass für jede Nullstelle \(\alpha\) der Funktion \(g\) eine dazugehörige konstante Lösung \(y(x)\equiv \alpha\) der gewöhnlichen Differentialgleichung \(y'=f(x)g(y)\) existiert, da \(y'(x)\equiv 0=g(\alpha)\equiv g(y(x))\). Diese Lösungen heißen triviale Lösungen (im Gegensatz zur allgemeinen Lösung).
Wenn die Voraussetzungen des folgenden Satzes erfüllt sind, dann können alle Lösungen einer Differentialgleichung getrennter Variablen entweder aus der allgemeinen Lösung oder den trivialen Lösungen abgeleitet werden.

Satz 2.
Betrachten wir das Anfangswertproblem \(y'=f(x,y),\ y(x_0)=y_0\).
- Wenn \(f\) stetig ist (als Funktion zweier Variablen), dann existiert mindestens eine Lösung in einem Intervall, welches den Punkt \(x_0\) enthält.
- Weiterhin, wenn \(f\) stetig differenzierbar bezüglich \(y\) ist, dann ist die Lösung, welche die Anfangswertbedingung erfüllt, eindeutig.
- Die Eindeutigkeit ist auch erfüllt, wenn neben (i) die Funktion \(f\) stetig differenzierbar bezüglich \(x\) ist und \(f(x_0,y_0)\neq 0\) gilt.

Der Beweis des Satzes basiert auf der Technik bekannt als Picard-Lindelöf-Iteration, welche von Emile Picard erfunden und von dem finnischen Mathematiker Ernst Lindelöf (1870-1946) und anderen weiterentwickelt wurde.
Durch Anwenden des vorherigen Satzes, können wir das folgende Ergebnis für Gleichungen getrennter Variablen formulieren.

Satz 3.
Betrachten wir eine Differentialgleichung getrennter Variablen \(y'=f(x)g(y)\), wobei \(f\) stetig und \(g\) stetig differenzierbar ist.
- Für jede Nullstelle \(\alpha\) der Funktion \(g\) existiert eine triviale Lösung \(y(x)\equiv \alpha =\) konstant.
- Alle anderen Lösungen (= die allgemeine Lösung) können durch Anwendung der vorher beschriebenen Methode ermittelt werden, d. h. die Variablen trennen und die Integrale berechnen.
Die Lösungskurven in jedem Punkt \((x_0,y_0)\) des Definitionsbereichs der Gleichung sind immer eindeutig. Insbesondere können die Kurven sich nicht überschneiden und es ist nicht möglich, dass sich eine einzelne Kurve in zwei oder mehr Teile aufteilt.
Die anderen Lösungskurven der gewöhnlichen Differentialgleichung können nicht die Kurven \(y=\alpha\) in Zusammenhang mit den trivialen Lösungen schneiden. Also gilt automatisch für alle anderen Lösungen die Bedingung \(g(y(x))\neq 0\)!
Beispiel 6.
Lösen wir die homogene lineare Differentialgleichung \(y'+p(x)y=0\) durch Anwenden der Methode für Gleichung getrennter Variablen.
Die Gleichung hat die triviale Lösung \(y_0(x)\equiv 0\). Da die anderen Lösungen nirgendwo den Wert 0 annehmen, gilt, dass
\[\begin{aligned} \frac{dy}{dx} &= y'= -p(x)y \\ &\Leftrightarrow \int\frac{\mathrm{d}y}{y} = -\int p(x)\, \mathrm{d}x +C_1 \\ &\Leftrightarrow \ln|y| = -P(x)+C_1 \\ &\Leftrightarrow |y| =e^{C_1-P(x)} \\ &\Leftrightarrow y=y(x)=\pm e^{C_1} e^{-P(x)} =Ce^{-P(x)}.\end{aligned}\]
Hierbei wurde der Ausdruck \(\pm e^{C_1}\) durch eine einfachere Konstante \(C\in\mathbb{R}\) ausgetauscht.

Die Euler Methode
In der Praxis ist es üblicherweise nicht möglich analytische Lösungen für Differentialgleichungen zu finden. In diesen Fällen bleibt als einzige Möglichkeit auf numerische Methoden zurückzugreifen. Ein markantes Beispiel dieser Art von Methode ist die sogenannte Euler Methode. Die Idee hinter der Methode ist die vorherige Beobachtung bei Richtungsfeldern: auch wenn wir die Lösung an sich nicht kennen, können wir dennoch die Tangenten der Lösungskurve bestimmen. Anders gesagt, suchen wir die Lösungen des folgenden Anfangswertproblems
\( \left\{\begin{align}y' = f(x,y) \\ y(x_0) = y_0. \end{align} \right. \)
In Eulers Methode beginnen wir den Lösungsprozess mit der Wahl der Schrittlänge \( h\) und dem Anwenden der Iterationsformel
\( \displaystyle y_{k+1} = y_k + hf(x_k, y_k). \)
Die Iteration beginnt beim Index \( \displaystyle k=0 \) durch Substituieren des gegebenen Anfangswertes auf der rechten Seite der Iterationsformel. Da \(f(x_k, y_k) = y'(x_k) \) ist die Steigung der Tangente der Lösung bei \(x_k \), für jeden Schritt bewegen wir uns mit einer Länge ausgedrückt durch die Schrittlänge in die Richtung der Tangente. Durch diesen Vorgang, entsteht ein Fehler, welcher mit zunehmender Schrittlänge steigt.
Beispiel 9.
Untersuchen wir die Lösung des Anfangswertproblems
\( \left\{\begin{align}y' = y \\ y(0) =1 \end{align} \right. \)
erhalten durch Anwendung der Euler Methode und vergleichen das Ergebnis mit der exakten Lösung \( \displaystyle g(x) = e^x. \)

7.3. Gewöhnliche Differentialgleichungen zweiter und höherer Ordnung

Für Differentialgleichungen höherer Ordnung ist es meistens unmöglich analytische Lösungen zu finden. In diesem Abschnitt stellen wir ein paar Sonderfälle vor, für die analytische Lösungen gefunden werden können. Die meisten dieser Fälle sind lineare Differentialgleichungen. Unser Fokus liegt auf Differentialgleichungen zweiter Ordnung, da diese häufiger praktische Anwendung finden und es wahrscheinlicher ist analytische Lösungen zu finden im Vergleich zu Differentialgleichungen dritter oder höherer Ordnung.

Lösen einer gewöhnlichen homogenen Differentialgleichung
Für lineare Gleichungen zweiter Ordnung gibt es keine einfache Weise eine allgemeine Lösung zu finden. Wir beginnen zuerst mit der Untersuchung einer homogenen Gleichung
\( y’’ + p(x)y’ + q(x)y = 0,\)
wobei \(p\) und \(q\) stetige Funktionen in ihrem Definitionsbereich sind. Dann gilt, dass
1) die Gleichung linear unabhängige Lösungen \(y_1\) und \(y_2\), genannt Fundamental-Lösungen, besitzt. Grob gesagt bedeutet lineare Unabhängigkeit, dass das Verhältnis \(y_2(x)/y_1(x)\) nicht konstant ist, so dass die Lösungen im Grund voneinander verschieden sind.
2) die allgemeine Lösung durch ein beliebiges linear unabhängiges Lösungspaar der Form \(y(x) = C_1y_1(x) + C_2y_2(x) \), wobei \( C_1\) und \( C_2\) Konstanten sind, ausgedrückt werden kann.
3) wenn die Anfangswerte \(y(x_0) = a, y'(x_0) = b\) fix sind, dann ist die Lösung eindeutig.
Eine allgemeine Methode die Fundamentallösungen \(y_1(x)\) und \(y_2(x)\) explizit zu finden existiert nicht. Um die Lösung zu finden, ist ein typischer Ansatz eine gute Vermutung über die Form der Lösung abzugeben und die Details durch Einsetzen in die Gleichung zu überprüfen.
Die obigen Ergebnisse können auch auf homogene Gleichungen höherer Ordnung verallgemeinert werden, aber dann nimmt die Anzahl an benötigten Fundamentallösungen und Anfangswerten in Anbetracht der Ordnung der Gleichung zu.
Beispiel 1.
Die Gleichung \( y’’-y= 0\) hat die Lösungen \( y = e^x\) und \( y = e^{-x}.\) Diese Lösungen sind linear unabhängig, so dass die allgemeine Lösung der Form \( y(x) = C_1e^x + C_2e^{-x}\) ist.

Gleichungen mit konstanten Koeffizienten
Betrachten wir einen relativ simplen Sonderfall einer Gleichung zweiter Ordnung
\( y’’ + py’ + qy = 0.\)
Um die Gleichung zu lösen, nutzen wir folgende Schätzung \( y(x) = e^{\lambda x}\), wobei \( \lambda\) eine unbekannte Konstante ist. Einsetzen der Vermutung in die Gleichung liefert
\( \lambda^2 e^{\lambda x} + p\lambda e^{\lambda x} + qe^{\lambda x} = 0.\)
\( \lambda^2 + p\lambda + q = 0.\)
Die letzte Gleichung heißt charakteristische Gleichung der gewöhnlichen Differentialgleichung. Das Lösen der charakteristischen Gleichung erlaubt es uns die Lösungen für die eigentliche gewöhnliche Differentialgleichung zu finden. Die Wurzel der charakteristischen Gleichung kann in drei Fälle aufgeteilt werden:
1) Die charakteristische Gleichung hat zwei unterscheidbare Wurzelergebnisse. Dann hat die gewöhnliche Differentialgleichung die Lösungen \(y_1(x) = e^{\lambda_1x} \) und \(y_2(x) = e^{\lambda_2x}. \)
2) Die charakteristische Gleichung hat ein Wurzelergebnis. Dann hat die gewöhnliche Differentialgleichung die Lösungen \(y_1(x) = e^{\lambda x} \) und \(y_2(x) = xe^{\lambda x}. \)
3) Die Wurzel der charakteristischen Gleichung hat die Form \(\lambda = a \pm bi.\) Dann hat die gewöhnliche Differentialgleichung die Lösungen \(y_1(x) = e^{ax}\cos(bx) \) und \(y_2(x) = e^{ax}\sin(bx). \)
Der zweite Fall kann durch Einsetzen in die ursprüngliche gewöhnliche Differentialgleichung erhalten werden und der dritte Fall kann durch Anwendung der Euler Formel \( e^{ix}=\cos x+i\sin x\) erhalten werden. Mit kleinen Änderungen können diese Ergebnisse auch für Differentialgleichungen höherer Ordnung verallgemeinert werden.
Dadurch dass die charakteristische Gleichung die exakt gleichen Koeffizienten wie die ursprüngliche gewöhnliche Differentialgleichung besitzt, ist es nicht notwendig diese nochmals für konkrete Beispiel zu erörtern: schreib sie einfach hin, indem du die gewöhnliche Differentialgleichung anschaust!
Beispiel 2.
Lösen wir das Anfangswertproblem
\( \left\{\begin{align}y'' -y' +2y=0 \\ y(0) = 1, y(1)=0 \end{align} \right. \)
Die charakteristische Gleichung ist \(\lambda^2 -\lambda -2 = 0,\) welche die Wurzeln \( \lambda_1 = 2\) und \( \lambda_2 = -1\) hat. Somit ist die allgemeine Lösung \( y(x) = C_1e^{2x} + C_2e^{-x}.\) Die Konstanten können durch Verwendung der Anfangswerte ermittelt werden:
\( \left\{\begin{align}C_1 + C_2=1 \\ e^2C_1 + e^{-1}C_2 = 0 \end{align} \right. \)
\( \left\{\begin{align}C_1 = -\frac{1}{e^3-1} \\ C_2 = \frac{e^3}{e^3-1} \end{align} \right. \)
Somit ist die allgemeine Lösung \( y(x) = \frac{1}{e^3-1} (-e^{2x} + e^{3-x}).\)
Beispiel 3.
Werfen wir einen Blick darauf wie die obigen Ergebnisse sich auf Gleichungen höherer Ordnung auswirken, indem wir Folgendes lösen
\( y^{(4)} - 4y''' +14y'' -20y' +25y = 0.\)
Nun ist die charakteristische Gleichung \( \lambda^4 - 4\lambda^3 +14\lambda^2 -20\lambda +25 = 0,\) welches die Wurzeln \( \lambda_1 = \lambda_2 = 1 + 2i\) und \( \lambda_3 = \lambda_4 = 1 - 2i\) liefert. Somit sind die Fundamentallösungen der gewöhnlichen Differentialgleichung \(e^x\sin(2x)\), \(e^x\cos(2x)\), \(xe^x\sin(2x)\) und \(xe^x\cos(2x)\). Die allgemeine Lösung ist
\( y = C_1e^x\sin(2x) + C_2e^x\cos(2x) + C_3xe^x\sin(2x) + C_4xe^x\cos(2x).\)

Eulers Differentialgleichung
Ein weiterer häufiger Typ von Differentialgleichungen zweiter Ordnung ist Eulers Differentialgleichung
\( x^2y'' + axy' + by = 0,\)
wobei \(a\) und \(b\) Konstanten sind. Eine Gleichung dieser Form wird anhand der Schätzung \(y(x)= x^r\) gelöst. Einsetzen liefert:
\( r^2 + (a-1)r + b = 0.\)
Durch Wurzelziehen dieser Gleichung erhalten wir die Lösungen für die gewöhnliche Differentialgleichung auf folgende Art und Weise:
1) Wenn die Wurzel eindeutig und reell ist, dann \( y_1(x)= |x|^{r_1}\) und \( y_2(x)= |x|^{r_2}\).
2) Wenn die Gleichung nur ein Wurzelergebnis liefert, dann \( y_1(x)= |x|^{r}\) und \( y_2(x)= |x|^{r}\ln |x|\).
3) Wenn das Ergebnis der Wurzel die Form \(r = a \pm bi\) hat, dann \( y_1(x)= |x|^{a}\cos(b\ln |x|)\) und \( y_2(x)= |x|^{a}\sin(b\ln |x|)\).
Beispiel 4.
Lösen wir die Gleichung \( x^2y'' - 3xy' + y = 0.\) Da wir merken, dass die Gleichung Eulers Differentialgleichung ist, gehen wir mit der Schätzung \(y= x^r\) vor. Durch Einsetzen der Schätzung in die Gleichung erhalten wir \( r(r-1)x^r - 3rx^r + x^r = 0 \Rightarrow r^2 - 4r + 1 = 0,\) welches \( r = 2 \pm \sqrt{3}\) liefert. Damit ist die allgemeine Lösung der gewöhnlichen Differentialgleichung
\(y = C_1 x^{2+\sqrt{3}} + C_2x^{2-\sqrt{3}}\).

Inhomogene lineare Differentialgleichungen
Die allgemeine Lösung einer inhomogenen Gleichung
\(y'' + p(x)y' + q(x)y = r(x)\)
ist die allgemeine Lösung der entsprechenden homogenen Gleichung \(+\) partikuläre Lösung zur inhomogenen Gleichung, d. h.
\(y(x) = C_1y_1(x) + C_2y_2(x) + y_0(x)\).
Die partikuläre Lösung \(y_0\) lässt sich normalerweise durch eine Schätzung, die der gleichen Form wie \(r(x)\) mit allgemeinen Koeffizienten entspricht. Durch Einsetzen dieser Schätzung in die gewöhnliche Differentialgleichung können wir die Koeffizienten auflösen, aber nur wenn die Schätzung von der korrekten Form ist.
In der unteren Tabelle haben wir eine Liste an möglichen Schätzungen für Differentialgleichungen zweiter Ordnung mit konstanten Koeffizienten zusammengestellt. Die Form der Schätzung hängt davon ab aus welcher Art von elementaren Funktionen \(r(x)\) besteht. Wenn \(r(x)\) eine Kombination aus mehreren verschiedenen elementaren Funktionen ist, dann müssen wir die entsprechenden Elemente für all diese Funktionen in unsere Vermutung einbeziehen. Die charakteristische Gleichung der entsprechenden homogenen Differentialgleichung ist \(P(\lambda)=\lambda^2+p\lambda+q=0\).
| \(r(x)\) enthält | die Schätzung besteht aus |
|---|---|
| Polynom von Grad \(n\) | \(A_0+A_1x+\dots +A_nx^n +A_{n+1}x^{n+1}\), wenn \(q=P(0)=0\)) |
| \(\sin kx,\ \cos kx\) | \(A\cos kx+B\sin kx\), wenn \(P(ik)\neq 0\) |
| \(\sin kx,\ \cos kx\) | \(Ax\cos kx+Bx\sin kx\), wenn \(P(ik)=0\) |
| \(e^{cx}\sin kx,\ e^{cx}\cos kx\) | \(Ae^{cx}\cos kx+Be^{cx}\sin kx\), wenn \(P(c+ik)\neq 0\) |
| \(e^{kx}\) | \(Ae^{kx}\), wenn \(P(k)\neq 0\) |
| \(e^{kx}\) | \(Axe^{kx}\), wenn \(P(k)=0\) and \(P'(k)\neq 0\) |
| \(e^{kx}\) | \(Ax^2e^{kx}\), wenn \(P(k)=P'(k)=0\) |
Anmerkung: Für Wurzeln von Polynomen zweiten Grades müssen wir beachten, dass
-
\(P(k)=0\) und \(P'(k)\neq 0\) \(\Leftrightarrow\) \(k\in\mathbb{R}\) ist eine Wurzel von \(P\).
-
\(P(k)=P'(k)= 0\) \(\Leftrightarrow\) \(k\in\mathbb{R}\) ist die einzige Wurzel von \(P\).
-
\(P(ik)\neq 0\) \(\Leftrightarrow\) \(ik\in\mathbb{C}\) ist kein Wurzelergebnis \(P\); d.h. \(\sin kx\) und \(\cos kx\) sind keine Lösungen der homogenen Gleichung.
Beispiel 5.
Suchen wir die allgemeine Lösung der gewöhnlichen Differentialgleichung \(y''+y'-6y=r(x)\), wenn
a) \(r(x)=12e^{-x}\)
b) \(r(x)=20e^{2x}\).
Die Lösungen sind von der Form \(y(x)=C_1e^{-3x}+C_2e^{2x}+y_0(x)\).
a) Durch Substitution der Vermutung \(y_0(x)=Ae^{-x},\) erhalten wir \((A -A -6A)e^{-x} =12e^{-x}\), welches für \(A=-2\) lösbar ist.
b) In diesem Fall ist die Schätzung von der Form \(Be^{2x}\) nutzlos, da es ein Teil der Lösung der entsprechenden homogenen Gleichung ist und liefert nur Null, wenn es in die linke Seite der gewöhnlichen Differentialgleichung eingesetzt wird. Hier ist die richtige Schätzung von der Form \(y_0(x)=Bxe^{2x}\). Einsetzen liefert
\[ (4B+2B-6B)xe^{2x}+(4B+B)e^{2x} = 20e^{2x}, \]welches für \(B=4\) lösbar ist.
Verwenden wir diese Werte für \(A\) und \(B\) können wir die allgemeinen Lösungen für die gegebenen Differentialgleichungen niederschreiben.
Beispiel 6.
Finden wir die Lösung der gewöhnlichen Differentialgleichung \(y''+y'-6y=12e^{-x}\) mit den Anfangswerten \(y(0)=0\), \(y'(0)=6\).
Basierend auf den vorherigen Beispielen ist die allgemeine Lösung von der Form \(y(x)=C_1e^{-3x}+C_2e^{2x}-2e^{-x}\). Differenzieren liefert \(y'(x)=-3C_1e^{-3x}+2C_2e^{2x}+2e^{-x}\). Durch die Anfangswerte erhalten wir das folgende Paar an Gleichungen:
\[ \begin{cases} 0=y(0)=C_1+C_2-2 &\\ 6=y'(0)=-3C_1+2C_2+2, &\\ \end{cases} \]welches für \(C_1=0\) und \(C_2=2\) lösbar ist. Damit ist die Lösung des Anfangswertproblems \(y(x)=2e^{2x}-2e^{-x}\).
Beispiel 7.
Eine typische Anwendung einer inhomogenen gewöhnlichen Differentialgleichung zweiter Ordnung ist ein RLC Stromkreislauf, der aus einem Widerstand (mit Widerstand \( R\)), einer Spule (mit Induktion \( L \)), einem Kondensator (mit Kapazität \( C \)) ) und einer zeitabhängigen elektromotorischen Kraft \( E(t)\) besteht Der elektrische Strom \( y(t)\) im Kreislauf erfüllt die gewöhnliche Differentialgleichung \[ Ly''+Ry'+\frac{1}{C}y=E'(t).\] Lösen wir diese gewöhnliche Differentialgleichung mit künstlich gewählten numerischen Werten von der Form \[ y''+10y'+61y=370\sin t.\]
Der homogene Teil hat eine charakteristische Gleichung von der Form \( \lambda^2+10\lambda +61=0\) mit Lösungen \( \lambda = -5\pm 6i\). Dies liefert die Lösungen \( y_1(t)=e^{-5t}\cos(6t)\) und \( y_2(t)=e^{-5t}\sin(6t) \) für die homogene Gleichung. Für eine partikuläre Lösung probieren wir \(y_0(t)=A\cos t +B\sin t\). Durch Einsetzen dieses in die inhomogene gewöhnliche Differentialgleichung und sammeln ähnlicher Terme liefert \[ (60A+10B)\cos t +(60B-10A)\sin t = 370\sin t. \] Die Gleichung ist für alle \( t\) erfüllt, (nur) wenn
\[ \begin{cases} 60A+10B=0 &\\ -10A+60B=370. &\\ \end{cases} \]welches für \( A=-1\) und \( B=6\) lösbar ist. Somit ist die allgemeine Lösung \[ y(t)=e^{-5t}(C_1\cos(6t)+C_2\sin(6t)) -\cos t+6\sin t .\] Merke, dass die exponentiellen Terme sehr schnell gegen Null gehen und schließlich der Stromfluss von der Form \[ y(t)\approx -\cos t+6\sin t\] oszilliert.

7.4. Exkurs: Coronamodellierung

Die Corona-Pandemie begann im Dezember 2019 in Wuhan, der Hauptstadt der chinesischen Provinz Hubei, und verbreitete sich von dort im Januar 2020 rasch in die ganze Welt aus. Da gegen das neuartige Virus SARS-CoV-2 kein Impfstoff bekannt war, wurde der Ausbreitung, Fallzahl, Krankheitsverläufen und Gegenmaßnahmen medial viel Aufmerksamkeit entgegengebracht und im Zuge dessen verschiedene Studien und mathematische Modelle diskutiert. Ein vielzitierter Leitspruch lautete „flatten the curve“, häufig kombiniert mit der Warnung vor dem exponentiellen Wachstum der Fallzahlen.
Das Robert-Koch-Institut (RKI) nennt allgemein die wichtigen Fragen, die Wissenschaftler möglichst schnell beantworten müssen, wenn irgendwo auf der Welt ein neuer Erreger auftritt:
„Wo liegt der Ursprungsort des neuen Erregers? Wo werden die nächsten Krankheitsfälle auftreten und wann? Und wieviele Menschen werden voraussichtlich infiziert? Schnelle Antworten auf diese Fragen sind notwendig, um durch Gegenmaßnahmen die weitere Verbreitung möglichst wirksam zu bekämpfen und potenziell verheerende Folgen zu vermeiden.“ (RKI, aufgerufen am 17.06.2020)
Die Situation ist hinreichend komplex, um verschiedene kleinere Problemstellungen in verschiedenen mathematischen Teilgebieten zu ermöglichen. Die Frage nach dem Ort der nächsten Krankheitsfälle ist eher geometrisch und spürt den Verkehrswegen und Vernetzungen der modernen Welt nach. Für die Beantwortung der Frage, wie viele Menschen sich mit dem Virus infizieren werden, können verschiedene Annahmen getroffen werden, die relativ leichte Modellierungen ermöglichen.

Modellierung mit einem SIR-Modell
Die Ausbreitung von Krankheiten wird im einfachsten Fall mit einem SIR-Modell modelliert. Dabei werden in einer Population drei verschiedene Gruppen als Zahlenwerte / Funktionswerte betrachtet und die Zusammenhänge der Veränderungen untersucht.
S: „susceptible“ – Darunter werden die Personen verstanden, die überhaupt krankt werden können, d.h. anfällig für die Krankheit sind. Eine bereits infizierte, immune oder verstorbene Person fällt aus dieser Gruppe heraus.
I: „infected“ – Darunter werden alle Personen gezählt, die zum jeweils betrachteten Zeitpunkt mit der Krankheit infiziert sind.
R: „removed“ – Darunter werden die Personen gezählt, die als aus dem Infektionsgeschehen entfernt angesehen werden können, d.h. genesene Personen, die – so eine einfache Modellannahme – auch eine Immunität gegen die Krankheit entwickelt haben, oder verstorbene Personen.
Die Veränderungen dieser Zahlenwerte hängt von der (Basis)Reproduktionszahl \( \beta \) und der Genesungsrate \( \gamma \) ab. Die Reproduktionszahl \( \beta \) gibt an, wie viele Personen eine infizierte Person im Durchschnitt jeweils abrnsteckt. In der Genesungsrate sind in unserem Modell genesene und verstorbene Personen zusammengefasst. Sie gibt an, wie viele infizierte Personen im Durchschnitt genesen/versterben.
Die Anzahl S ändert sich nur durch die neu infizierten Personen. Änderungsraten können wir durch Ableitungen mathematisch fassen, also für S' folgende Formel aufstellen: \( S'(t) = -\beta \cdot S(t) \cdot I(t) \). Die Anzahl der Infizierten I wird durch die Ansteckung von noch nicht infizierten Personen größer und durch die Genesung kleiner, also ergibt sich: \( I'(t) = \beta \cdot S(t) \cdot I(t) - \gamma\cdot I(t) \). Für R' ergibt sich aus der letzten Gleichung \( R'(t) = \gamma \cdot I(t) \).
Diese drei Differentialgleichungen lassen sich für passende Anfangswerte z.B. mit GeoGebra lösen und untersuchen. Das Video zeigt, wie das gehen kann. Wir haben die Parameter als Schieberegler dynamisch mit einbezogen, damit auch deren Einfluss untersucht werden kann, etwa um die Hintergründe und Wirksamkeit von Kontaktbeschränkungen und Mund-Nasen-Masken zu untersuchen.
Das hier dargestellte Modell stellt eine sehr einfach Variante dar, die mit nur zwei Faktoren auskommt und eine Menge Annahmen macht, die der Realität teilweise nicht gerecht werden:
- Jedes Individuum kann nur einmal infiziert werden.
- Infizierte sind sofort ansteckend, eine Inkubationszeit wird nicht abgebildet.
- Reproduktionszahl und Genesungsrate sind konstant.
- Es wird keine Unterscheidung getroffen zwischen genesenen und verstorbenen Personen, der allerdings in der Realität enorm wichtig ist.

Aufgabe: Erstellen Sie eine GeoGebra-Simulation wie im Video gezeigt. Ergänzen Sie dann eine Sterblichkeitsrate (lethality rate) als Schieberegler und die Zahl D der Verstorbenen („deceased“).

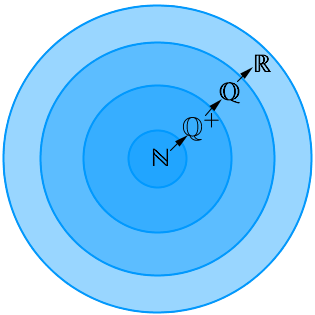
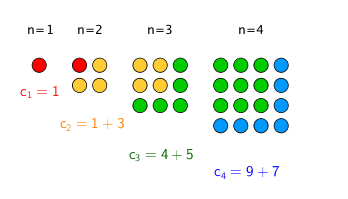
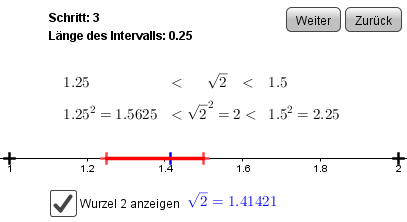
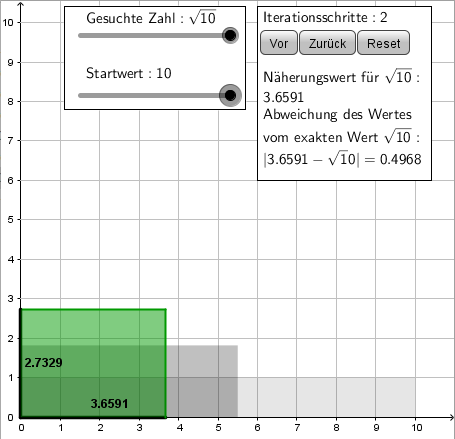
 I \)
I \)