Grundlagen der anwendungsbezogenen Hochschulmathematik
6. Integralrechnung
6.1. Grundlagen


Definition 1:
Es sei \([a,b]\) ein echtes kompaktes Intervall. Eine Zerlegung von I ist ein (n+a)-Tupel \[Z = ( x_0, x_1, x_2, ..., x_{n-1}, x_n) \] mit einer beliebigen natürlichen Zahl n und reellen Zahlen \(x_0, x_1, x_2, ..., x_{n-1}, x_n \), die \[x_0 < x_1 < x_2 <...<x_{n-1}< x_n = b\] erfüllen. Die Punkte \(x_{i} \) heißen Teilpunkte der Zerlegung \(Z\), und die positive Zahl \[ \|Z\| := \max_{1 \leq i \leq n} (x_i - x_{i-1}). \] heißt die Feinheit der Zerlegung.Da \(f\) beschränkt ist, existieren auf jedem Teilintervall \([t_{i-1},t_i]\) Supremum (\(M_i\)) und Infimum (\(m_i\)) von \(f\).
Dann heißen
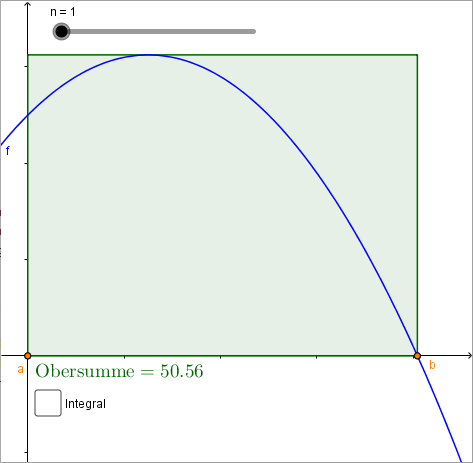
\[\sum^{n}_{i=1} M_i\cdot (t_i - t_{i-1})\]
Obersumme und
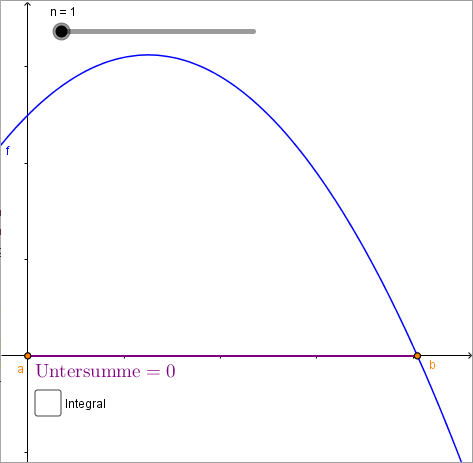
\[\sum^{n}_{i=1} m_i\cdot (t_i - t_{i-1})\]
Untersumme von \(f\) zur Zerlegung \(Z\).
Mit deren Hilfe lässt sich das Integral definieren:

Definition 2
\(f\) sei eine auf einem abgeschlossenen Intervall \([a,b]\subset\mathbb{R}\) definierte und dort beschränkte Funktion. Ist das Supremum \(S\) aller über \([a,b]\) gebildeten Untersummen gleich dem Infimum \(I\) aller über \([a,b]\) gebildeten Obersummen, so heißt \(S=I\) das bestimmte Integral von \(f\) über dem Intervall \([a,b]\) und wird mit
\[\int^{b}_a f(x)\;dx\]
bezeichnet. In diesem Fall heißt die Funktion \(f\) integrierbar über \([a,b]\).
Es gilt: \(\begin{eqnarray*}\int\limits^a_a f(x)\,\mathrm d{x} & := & 0 \])

Falls \[ \lim_{n\to\infty} U_n = \lim_{n\to\infty} O_n, \] dann nennt man diese Zahl das bestimmte Integral von \(f\) über \([a,b]\). Sie wird bezeichnet mit: \[ \int^{b}_a f(x)\;dx \] \(f\) heißt in diesem Fall integrierbar über \([a,b]\).
Satz 1 (Integrabilitätskriterium von Riemann)
\(f\) sei eine auf einem abgeschlossenen Intervall \([a,b]\subset\mathbb{R}\) definierte und dort beschränkte Funktion. Dann sind folgende Aussagen äquivalent:
\( f \)ist Riemann-integrierbar.
und
Für jedes \(\mathcal{E}\) gibt es eine Partition \(P\), für die \(O_n (f,P)-U_n (f,P) < \mathcal{E}\) gilt.

Satz 1 (Integrierbarkeit von Funktionen)
- Ist \(f\) auf \([a,b]\) monoton und beschränkt, so ist \(f\) auf \([a,b]\) integrierbar.
- Ist \(f\) auf \([a,b]\) stetig, so ist \(f\) auf \([a,b]\) integrierbar.
Eine Funktion heißt monoton, wenn sie monoton fallend oder monoton steigend ist.