Grundlagen der anwendungsbezogenen Hochschulmathematik
4. Funktionen II
4.4. Eigenschaften stetiger Funktionen

Eigenschaften stetiger Funktionen
Dieser Anschnitt beinhaltet einige wichtige Eigenschaften stetiger Funktionen. Wir starten mit dem Zwischenwertsatz (Satz von Bolzano). Dieser Satz besagt, dass eine Funktion, wenn sie auf einem (abgeschlossenen) Intervall stetig ist, jeden Funktionswert zwischen den Funktionswerten an den Endpunkten annimmt. Intuitiv folgt das sofort aus der Tatsache, dass die Funktion \(f\) stetig auf dem Intervall ist.

Satz 1.
Es sei\(f(x) \colon \left[ a,b \right] \to \mathbb{R} \) eine auf ihrer Definitionsmenge stetige Funktion und \( f(a) < s < f(b) \). Dann gibt es eine Stelle \( x_0 \in \left[ a,b \right] \) mit \( f(x_0) = s \).
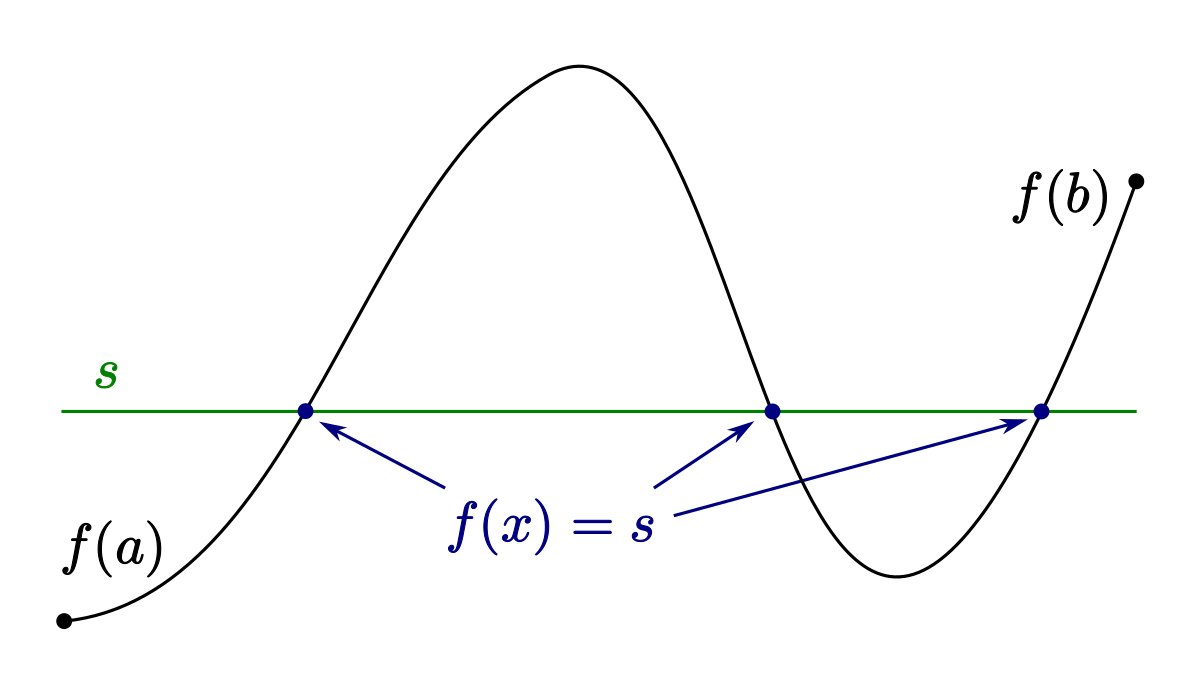
Beispiel 1.
Es sei \( f(x) \colon \mathbb{R} \to \mathbb{R} \) die Funktion \( f(x) = x^3 - 2x^2 + 3x - 4 \). Gibt es eine Stelle \( x_0 \), für die \( f(x) = 0 \) gilt?
Da \( f(x) \) ein Polynom ist, ist \(f\) stetig. Es gilt
\[ f(-10) = - 1000 - 200 - 30 - 4 = -1234 \]und
\[ f(10) = 1000 - 200 + 30 - 4 = 826 \]Aus dem Zwischenwertsatz folgt, dass es im Intervall \([-10,10]\) für jeden Wert \(s\) mit \( -1234 < s < 826 \) ein zugehöriges \( x \) mit \(f(x)=s\) existiert. Für \( s = 0 \) gibt es daher ein \( x_0 \) mit \( f(x_0) = 0 \).
Mit Hilfe dieses Satzes ist es jedoch nicht möglich, ein mögliches \( x_0 \) zu finden. Man weiß auf Grund des Satzes nur, dass ein solches \(x_0\) existiert.
Beispiel 2.
Gegeben sei die Temperatur am Nordpol und am "diametral entgegengesetzen" Punkt (dem Südpol). Die Differenz der Temperaturen sei \( \alpha \). Wir bewegen uns nun um die Erde vom Nord- zum Südpol und bestimmen die Temperaturdifferenz an jedem Punkt dieses Weges zum diametral entgegengesetzen Punkt. Wenn wir am Südpol angekommen sind, ist diese Differenz \(-\alpha\) (wir müssen uns dazu hinreichend schnell bewegen). Da die Temperaturänderung eine stetige Funktion ist, gibt es wenigstens einen Punkt auf unserem Weg, an dem die selbe Temperatur wie an dem diamentral entgegengesetzten Punkt vorliegt (also die Differenztemperatur \(0\) ist).
Beispiel 3.
Jedes Polynom ungeraden Grades hat wenigstens eine (reelle) Nullstelle
Es sei \(h(x) = a_n x^n + a_{n-1} x^{n-1} + \ldots + a_1 x + a_0\) ein Polymon \(n.ten\) Grades, wobei \( n \) ungerade und \(a_n\not=0\) ist. Offensichtlich ist einer der Grenzwerte \(\lim\limits_{x\to\infty}h(x)\) und \(\lim\limits_{x\to-\infty}h(x)\) plus unendlich und einer minus unendlich (da die Funktion \(h\) ungeraden Grad hat). Wir erhalten also:
\[ \lim\limits_{x \to +\infty} \left( a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0 \right) =\] \[ = \lim\limits_{x \to +\infty} x^n \cdot \left( a_n + a_{n-1} \cdot \frac{1}{x} + a_{n-2} \cdot \frac{1}{x^2} + \ldots + a_1 \cdot \frac{1}{x^{n-1}} + a_0 \cdot \frac{1}{x^n} \right) =\] \[ = \lim\limits_{x \to +\infty} \left( a_n x^n \right) = \begin{cases} +\infty \text{, when } a_n > 0 \\ -\infty \text{, when } a_n < 0 \end{cases} \]Analog streben die Werte von \( h(x) \) für \(x \to -\infty \) gegen \( -\infty \), falls \( a_n \) positiv und gegen \( +\infty \) für negatives \( a_n \). Daher gibt es in jedem Fall positive und negative Funktionswerte.
Da Polynome stetige Funktionen sind, folgt aus dem Zwischenwertsatz, dass die Funktion \( h\) wenigstens eine reelle Nullstelle hat.
Bemerkung: Die obige Aussage ist für Polynome geraden Grades im Allgemeinen falsch. Für gerades \( n \) sind die beiden Grenzwerte entweder plus unendlich oder minus unendlich und haben damit das gleiche Vorzeichen. Daher funktioniert die Idee von Beispiel 3 nicht in diesem Fall.

Satz 2.
Eine stetige Funktion \(f \colon \left[ a, b \right] \to \mathbb{R} \) ist beschränkt.

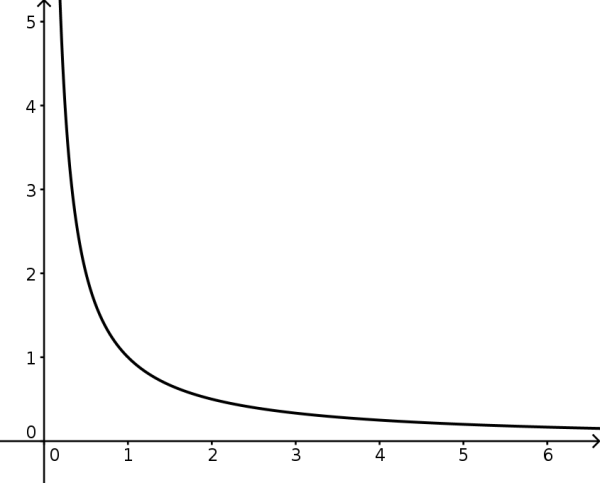
Bemerkung: Man beachte, dass die obige Aussage für offene Intervalle \( \left] a, b \right[ \) nicht gilt. Dazu betrachten wir die Funktion \( f(x) = \frac{1}{x} \) im Intervall \( \left] 0, 1 \right[ \). Wenn \(x\) von rechts gegen \(0\) strebt, so wird der Funktionswert \(f(x)\) beliebig groß. Also ist die Funktion zwar stetig, aber unbeschränkt auf \( \left] 0, 1 \right[ \).
Warum ist diese Eigenschaft so wichtig?
Beschränkte stetige Funktionen nehmen auf jedem abgeschlossenen Intervall \( \left[ a, b \right] \) ihr Maximum und Minimum an. Ferner bedeutet dies, dass die stetige Funktion \(f\) das abgeschlossene Intervall \( \left[ a, b \right] \) auf das abgeschlossene Intervall \( \left[ c, d \right] \) abbildet. Wir werden dies in Theorem 3 beweisen.

Satz 3.
Es sei \( f \colon \left[ a, b \right] \to \mathbb{R} \) eine stetige Funktion. Dann gibt es Werte \( c, d \in \left[ a, b \right] \), so dass \( f(c) \leq f(x) \leq f(d) \) für alle \( x \in \left[ a, b \right] \) gilt.


Numerisches Lösen
Neben dem graphischen Lösen gibt es verschiedene numerische Methoden, um näherungsweise Lösungen für Gleichungen zu finden. Numerische Methoden, sowie algebraische Methoden, werden oft zusammen mit Computern oder geeigneter Software angewandt, aber auch beim Benutzen der Software sollte man die Prinzipien der Methoden, auf denen die Algorithmen basieren, verstehen. Ebenso wichtig ist zu wissen, dass abhängig von der Methode das Ergebnis nur eine Nullstelle liefert, auch wenn die Gleichung mehrere Nullstellen besitzt
Unter den einfachsten numerischen Lösungsmethoden für Gleichungen ist das Intervallhalbierungs-Verfahren (Bisektion), welche auf dem Satz von Bolzano-Weierstraß basiert: wenn eine stetige Funktion negativ in einem Endpunkt eines Intervalls und positiv am anderen ist, dann muss es eine Nullstelle der Funktion irgendwo in diesem Intervall geben. Im Intervallhalbierungsverfahren wird das Intervall wiederholt halbiert, während das Vorzeichen der Funktion im Mittelpunkt eines Intervalls (oder nahe dem Mittelpunkt) überprüft wird.
Beispiel 3.
Lösungen der Gleichung
Lösen wir die Gleichung \[ 2^x - x -4 = 0, \] wobei \( x>0 \).
Leicht sieht man, dass die Gleichung, welche auch umgeschrieben werden kann als \[ 2^x = x+4, \] ihre einzige positive Nullstelle irgendwo zwischen den Punkten \( x=2 \) und \( x=3 \) hat. Dies kann zum Beispiel durch skizzieren der Kurve \( y=2^x \) und der Geraden \( y=x+4 \), veranschaulicht werden, siehe Bild unten. Tatsächlich ist das Bild sehr viel genauer als notwendig: eine grobe Skizze mit Stift und Papier sollte genügen.
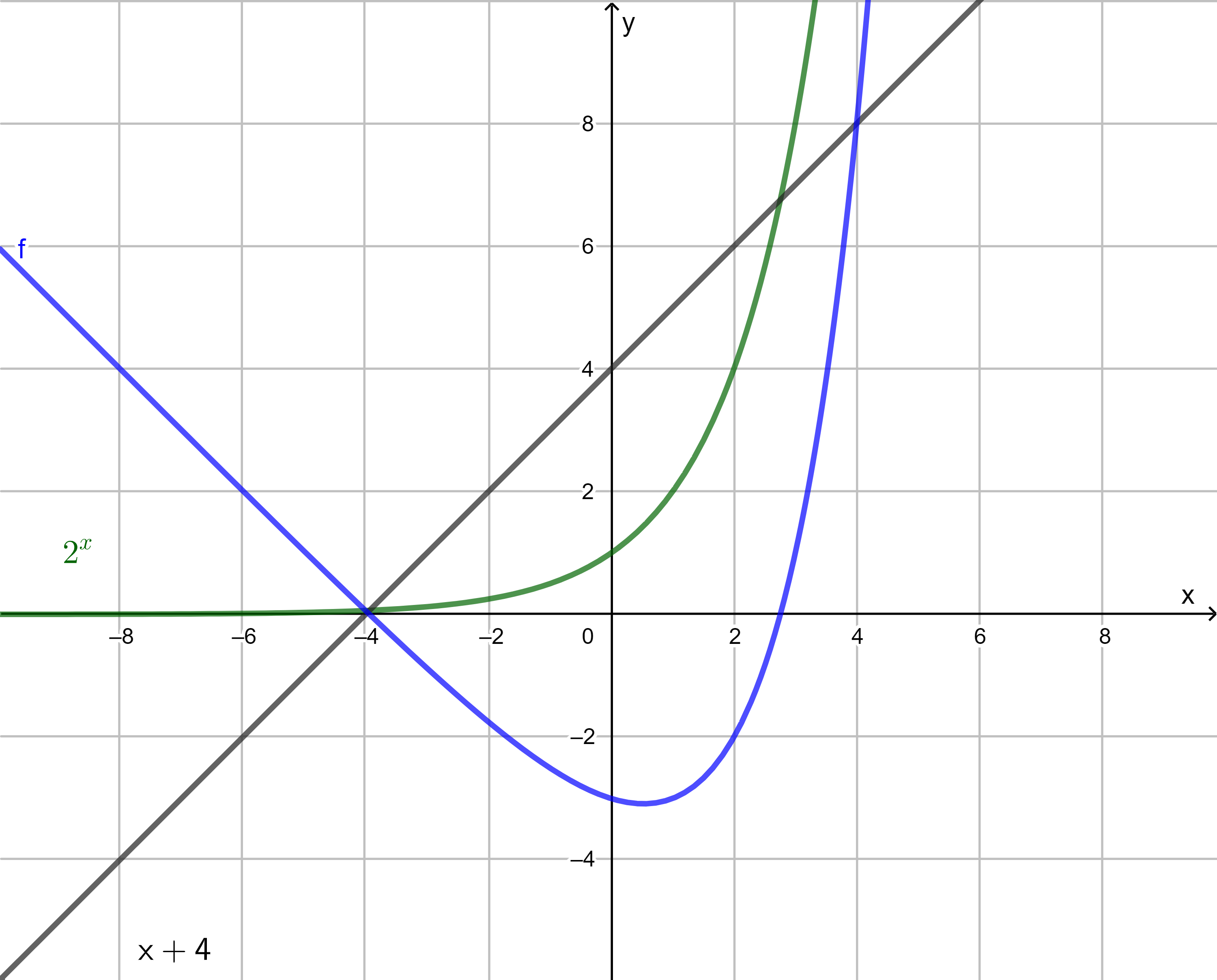
Nun kann die angenäherte Nullstelle wesentlich genauer bestimmt werden, indem Bisektion auf die Funktion angewandt wird \( f(x)=2^x-x-4 \):
- \( f(2) = -2 < 0 \) und \(f(3) = 1 > 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2 , 3[ \) (wie wir bereits wussten)
- \( f(2{,}5) \approx -0{,}84 < 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2{,}5 \hspace{0.1cm}; \hspace{0.1cm} 3[ \)
- \( f(2{,}75) \approx -0{,}02 < 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2{,}75 \hspace{0.1cm}; \hspace{0.1cm} 3[\)
- \( f(2{,}85) \approx 0{,}36 > 0 \Rightarrow \) ist eine Nullstelle auf dem Intervall \( ]2{,}75 \hspace{0.1cm}; \hspace{0.1cm} 2{,}85[ \)
Nun kennen wir die Nullstelle mit einer Genauigkeit von einer Nachkommastelle: \( x \approx 2{,}8 \).
Das Intervallhalbierungsverfahren ist nicht sehr effizient: wenn eine höhere Genauigkeit notwendig ist, kann die Zahl der Bisektionen sehr groß sein. Es gibt effizientere und raffiniertere numerische Lösungsmethoden, wie das Newton-Verfahren. Wie oben zu sehen ist, kann graphisches Lösen in Verbindung mit numerischem Lösen angewandt werden: erstmal eine sehr grobe Abschätzung für eine Nullstelle graphisch finden und dann die Abschätzung durch numerischen Methoden verfeinern.

Übung 1.
Die Gleichung \[ x^3+\ln x = 0 \] hat eine Lösung im Intervall \( [0,5 ; 1] \). Bestimme die Nullstelle auf zwei Nachkommastellen genau mithilfe des Intervallhalbierungsverfahrens.

