Grundlagen der anwendungsbezogenen Hochschulmathematik
3. Funktionen I
3.2. Eigenschaften von Funktionen


Eigenschaften von Funktionen
In diesem Kapitel beschäftigen wir uns mit grundlegenden Eigenschaften von Funktionen:
- Symmetrieeigenschaften
- Monotonie
- besondere Punkte von Funktionen: Nullstellen, Schnittstellen und Extrema

Symmetrieeigenschaften
Funktionen können symmetrisch sein. Dies bezieht sich primär auf den Graphen der Funktion und verhält sich wie schon bekannte Symmetrie. Man unterscheidet Achsensymmetrie und Punktsymmetrie.
Beispiel 1
Beispiele für Achsensymmetrie sind die Cosinusfunktion \( f(x)=cos(x) \)oder auch die Funktion \( g(x)=x² \)
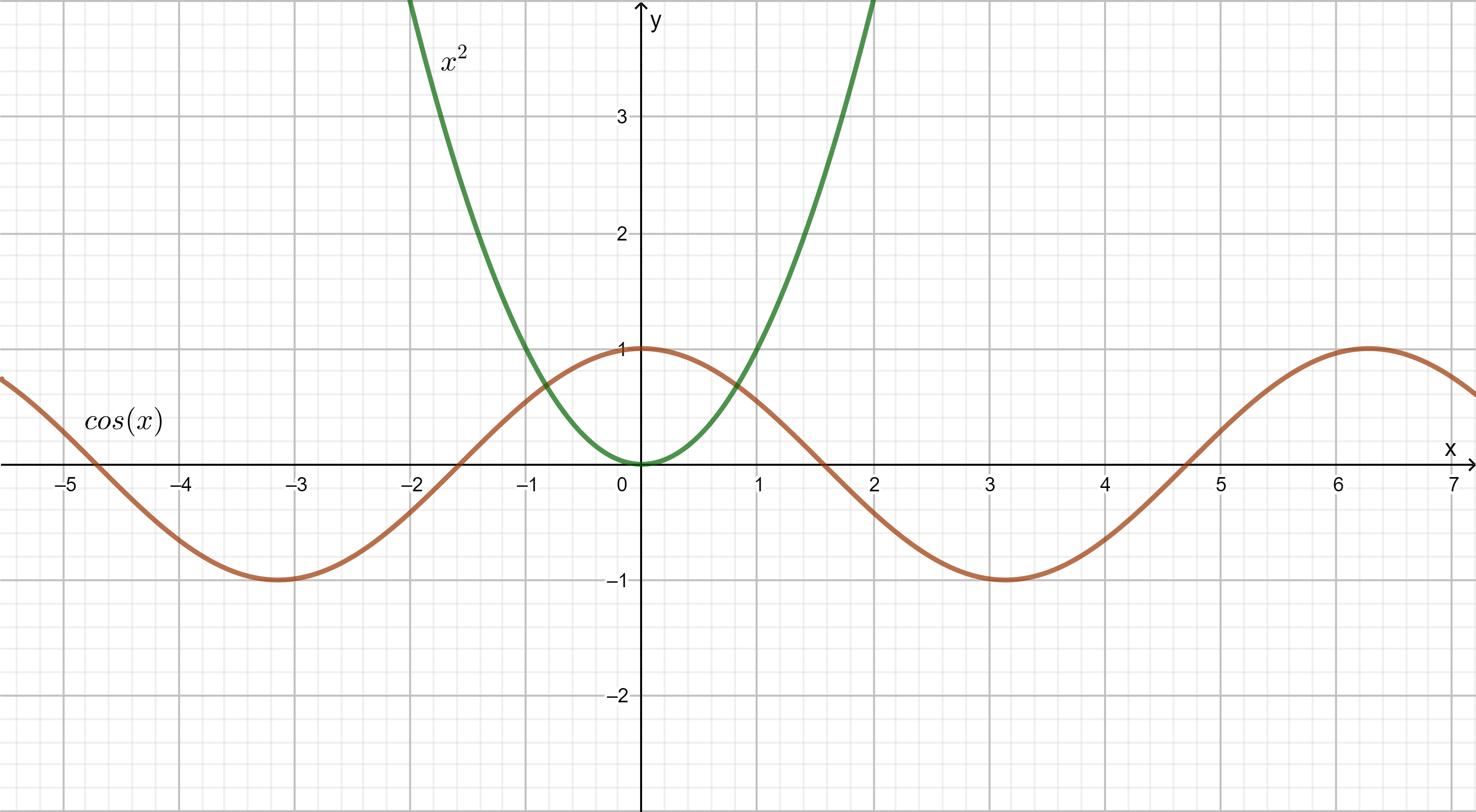

Definition Achsensymmetrie:
Eine Funktion ist achsensymmetrisch bezüglich der Gerade \( x=h \), die parallel zur y-Achse ist, wenn \( f(h-x) = f(h+x) \) für alle x-Werte aus dem Definitionsbereich erfüllt ist.
Ein Spezialfall ist \( h=0 \):
Gilt \( f(x) = f(-x) \) für alle x-Werte aus dem Definitionsbereich, wird diese Funktion ist achsensymmetrisch bezüglich der y-Achse bezeichnet.
Meist wird der Zusatz "bezüglich der y-Achse" im Spezialfall weggelassen. Spricht man von einer achsensymmetrischen Funktion ist damit für gewöhnlich die Bedingung \( f(x) = f(-x) \) für alle x-Werte aus dem Definitionsbereich gemeint.
Geometrisch interpretiert ist Achsensymmetrie bezüglich einer Geraden bedeutet, dass die Funktion an der Geraden gespiegelt ist. Alle Punkte, die jeweils gleichweit von der Geraden entfernt sind, haben den selben y-Wert.

Beispiel 2
Ein einfaches Beispiel hierfür ist \( f(x)=x \) als im Ursprung punktsymmetrische Funktion. Auch die Sinusfunktion \( g(x)=sin(x) \) ist punktsymmetrisch.

Definition Punktsymmetrie:
Eine Funktion ist punktsymmetrisch, falls \(f(a+x)-b=-(f(a-x)-b) \) für alle x-Werte erfüllt ist.
Ist sie sogar punktsymmetrisch im Ursprung, so gilt \( f(-x) = -f(x) \) .
Die Punktsymmetrie ist eine spezielle Form der Drehsymmetrie. Der Graph der Funktion ist drehsymmetrisch mit dem Drehwinkel \( 180° \). Bei der Punktsymmetrie kann man weiter differenzieren. Eine Funktion kann mit der obigen Definition punktsymmetrisch im Ursprung sein, hier gilt die Formel \( f(-x) = -f(x) \). Meistens ist Punktsymmetrie im Ursprung gemeint. Funktionen können jedoch auch punktsymmetrisch in jedem anderen Punkt \( (a/b) \) des Koordinatensystem sein. In diesem Fall gilt \( f(a+x)-b=-(f(a-x)-b) \).
Im nebenstehenden Applet können Sie Funktionen auf Punktsymmetrie im Ursprung prüfen.

Beispiel 3
Die schon bei der Achsensymmetrie betrachtete Cosinusfunktion ist nicht punktsymmetrisch im Ursprung, aber in jeder ihrer Nullstellen.
Die Funktion \( y = x^3-3x^2+2 \) ist punktsymmetrisch im Punkt \( (1/0) \) (A).

Aufgabe:
Überprüfe ob die Funktionen \( f(x) = 7x^7 - 6x^6 + 5x^5 - 4x^4 \) und \( f(x) =\frac{4}{x} \) eine Symmetrie aufweisen.

Monotonieeigenschaften
Monotonie beschreibt den groben Verlauf einer Funktion, ob sie in einem bestimmten Intervall steigt, fällt oder konstant bleibt. Man unterscheidet streng monoton steigend, monoton steigend, monoton fallend und streng monoton fallend. Weißt eine Funktion ein einheitliches Monotonieverhalten auf ihrem kompletten Definitionsbereich auf, so nennt man die Funktion (streng) monoton steigend bzw. fallend. Neben den untenstehenden Definitionen wird Monotonie oft über die Ableitung, die der Steigung der Funktion entspricht, bestimmt.Beispiel 4
Die in Beispiel 3 betrachtete Funktion \( f(x) = x^3-3x^2+2 \) weißt kein einheitliches Monotonieverhalten auf. Die Monotonie änderst sich stets an den Extrempunkten. Die Funktion wächst bis zum Punkt \((0,2)\). Im Intervall \([0,2]\) fällt die Funktion. Danach wächst die Funktion wieder.
Definition monoton wachsend:
Eine Funktion heißt auf einem Intervall I monoton wachsend, wenn für alle x-Werte dieses Intervalls mit \( x_1<x_2 \) gilt, dass \( f(x_1) \leq f(x_2) \) ist.
Definition streng monoton wachsend:
Gilt auf dem Intervall sogar \( f(x_1) < f(x_2) \) für \( x_1 < x_2 \), so ist die Funktion auf diesem streng monoton wachsend.

Beispiel 5
Die Exponentialfunktion \(e^x\), welche wir im Verlauf des Kapitels noch genauer betrachten und \( f(x)=x \) sind streng monoton wachsende Funktionen.
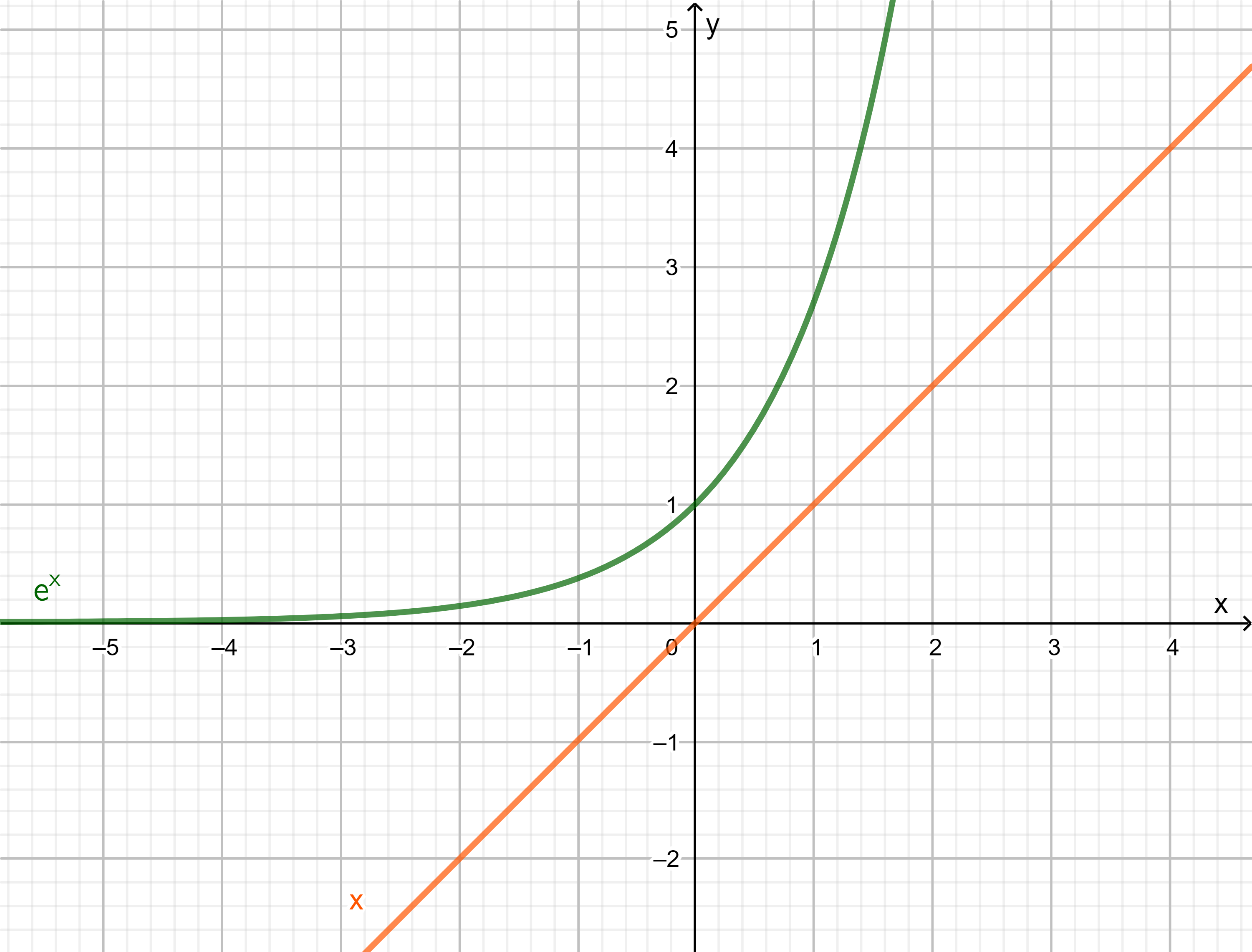

Definition monoton fallend:
Man bezeichnet eine Funktion auf einem Intervall I monoton fallend, falls für alle x-Werte \( \in I\) gilt:
\( f(x_1) \geq f(x_2) \) für \( x_1 < x_2 \)
Definition streng monoton fallend:
Man bezeichnet eine Funktion auf einem Intervall I streng monoton fallend, falls für alle x-Werte \( \in I\) gilt:
\( f(x_1) > f(x_2) \) für \( x_1 < x_2 \)
Beispiel 6
Die Funktion \( f(x) = -x^3 \) ist auf ihrem ganzen Definitionsbereich streng monoton fallend. Ihre Steigung ist zu jeder Zeit negativ und keine zwei verschiedenen y-Werte sind gleich.

Nullstellen und Schnittstellen von Funktionen
Nullstellen einer Funktion sind Punkte, in denen ihr y-Wert gleich Null ist. Die Funktion schneidet oder berührt hier somit die x-Achse. Funktionen müssen keine Nullstellen haben.
Hat mein ein Polynom mit Grad n, so besitzt dieses höchsten n Nullstellen.
Beispiel 7
Die Sinus- und Cosinusfunktion haben sehr viele Nullstellen, immer im Abstand von \(2\pi\).
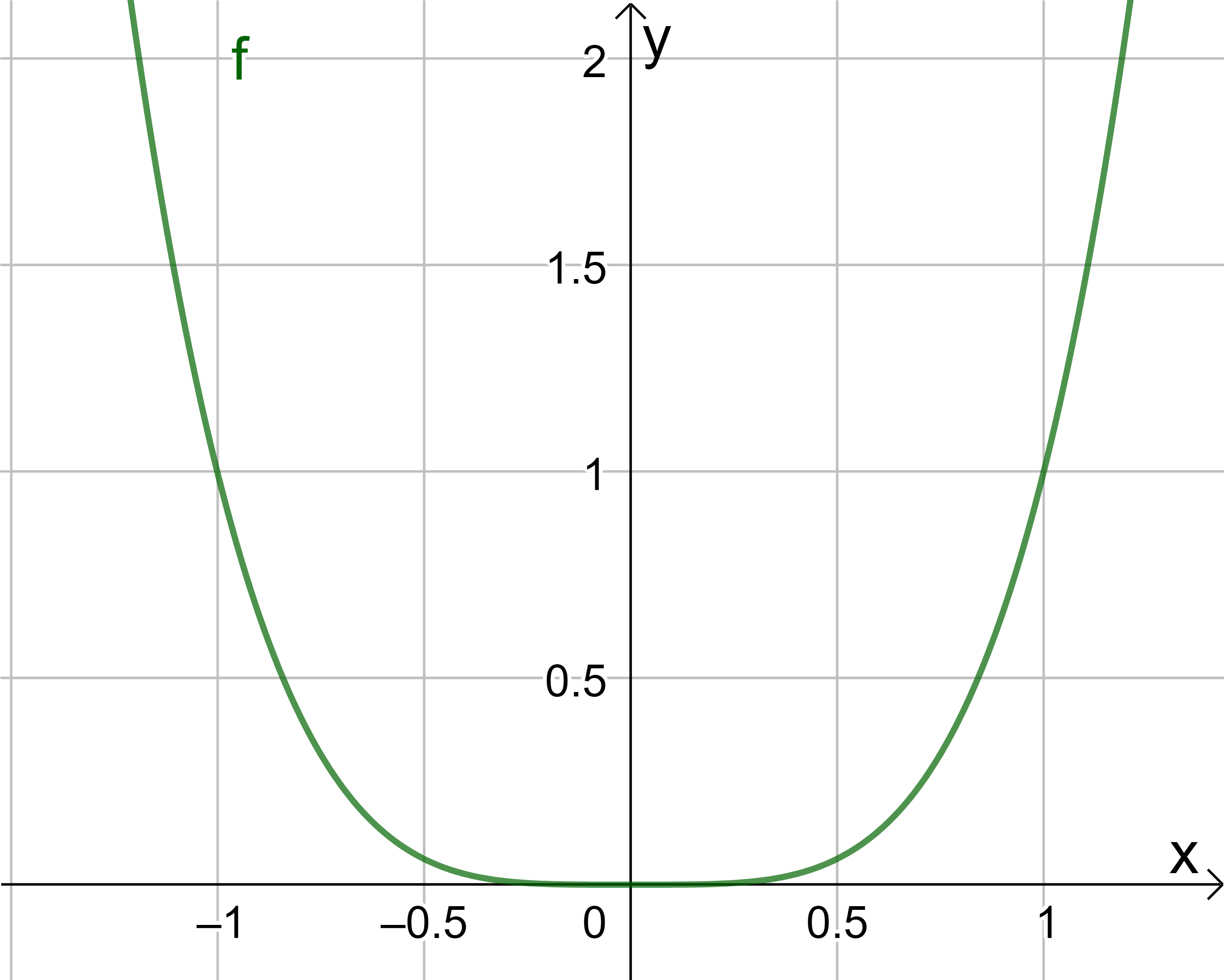
Beispiel 8
Die Funktion \( f(x) = x^4 \) berührt die x-Achse im Punkt \((0/0)\). Es liegt hier eine Nullstelle vor, auch wenn die x-Achse nicht geschnitten wird.

Definition Nullstelle:
Eine Funktion \(f\) mit Definitionsbereich \(D\) hat im Punkt \( x \in D \) eine Nullstelle, falls \( f(x) = 0 \) gilt.
Um die Nullstellen einer Funktion zu ermitteln, setzt man den y-Wert gleich Null. Man erhält die Gleichung \( f(x)=0 \). Indem man den Funktionsterm für \(f(x)\) einsetzt und diese Gleichung nach \(x\) auflöst, erhält man alle Nullstellen der Funktion.
Beispiel 9
Die Funktion \( f(x) = e^x \) besitzt keine Nullstelle.

Anwenden von Nullstellen: Graphisches Lösen von Gleichungen
Eine Gleichung kann graphisch gelöst werden, indem beide Seiten der Gleichung durch einen Kurve im Koordinatensystem repräsentiert werden und man die Schnittpunkte der Kurven ausfindig macht. Wenn die Gleichung in der Form \( f(x)=0 \) geschrieben ist, können die Nullstellen in den Punkten, wo die Kurve \( y=f(x) \) die \( x \)-Achse schneidet, gefunden werden.
Graphisches Lösen ist eine annähernde Methode, wobei das algebraische Lösen benutzt wird und exakte Lösungen der Gleichung zu finden. Es gibt eine Vielzahl an Gleichungen, bei denen es zu schwer oder gar unmöglich ist sie algebraisch zu lösen, dann werden approximierende Methoden gebraucht.

Extremwerte
Bei Extremwerten einer Funktion unterscheidet man zwischen Minima und Maxima. Ein Minimum bezeichnet einen Tiefpunkt der Funktionswerte, beziehungsweise auch des Funktionsgraphen, ein Maximum hingegen stellt einen Hochpunkt der Funktionswerte, beziehungsweiße des Funktionsgraphen dar.Man unterscheidet allgemein zwischen globalen und lokalen Extrempunkten.
Bei lokalen Maxima differenziert man weiterhin zwischen strikten und nicht strikten lokalen Maxima. Analog unterscheidet man die verschiedenen Formen von Minima. Dies behandeln wir im Kapitel Funktionen II, Extremwerte genauer.
Beispiel 10
Ein striktes lokales Maximum kann man in der schon oben betrachteten Funktion \( y=x^3-3x^2+2 \) bei \( x=0 \) finden.
Auch die Sinus- und Cosinusfunktion haben viele lokale Extremwerte, jedoch keine globalen.

Definition lokales Maximum:
Ein striktes lokales Maximum in \( x \) liegt vor, wenn \( f(a) < f(x) \) für alle \( a I \) für ein bestimmtes Intervall I. Bei einem lokalen Maximum, welches nicht strikt ist, kann es sich statt einem festen Punkt \( x \) auch um ein Intervall handeln, für welches die Definition zutrifft.
Definition lokales Minimum:
Analog liegt ein striktes lokales Minimum in \( x \) vor, wenn \( f(a) > f(x) \) für alle \( a I \) für ein bestimmtes Intervall I. Bei einem lokalen Minimum, welches nicht strikt ist, kann es sich statt einem festen Punkt \( x \) auch um ein Intervall handeln, für welches die Definition zutrifft.

Beispiel 13
Bei der Funktion \( f(x)=x² \) liegt somit am Urspung \( (0/0) \) ein globales Minimum vor. Die gespiegelte Funktion \(f(x)=-x²\) weist in diesem Punkt hingegen ein globales Maximum auf.
Definition globales Maximum:
Wenn wenn \( f(a) < f(x) \) für alle \( a D \) für den kompletten Definitionsbereich D gilt, so liegt in \( x \) ein globales Maximum vor.
Definition globales Minimum:
Für ein globales Minimum in \( x \) muss gelten \( f(a) < f(x) \) für alle \( a D \) im kompletten Definitionsbereich D.
Beispiel 14
Die Funktion \( f(x)=x^3 \) hat zwar weder ein Maximum noch ein Minimum, dafür jedoch einen Terrassenpunkt.


 I \)
I \)