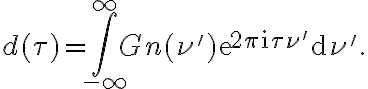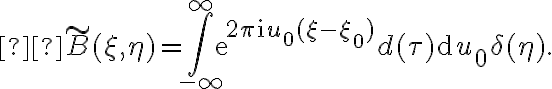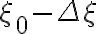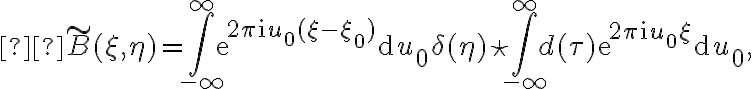Lecture - Fundamental Concepts
4. Receiver Response
4.4. Bandwidth smearing
As already seen in Chapt. 2 Sect. 4.2, the sensitivity of radio-interferometrical measurements depends on the effective area of the telescopes 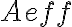 and the bandwidth
and the bandwidth 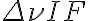 . The larger
. The larger 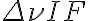 , the higher the sensitivity. However, using a large bandwidth is problematic, since the Fourier relation between brightness distribution and visibility is only valid for monochromatic signals. Therefore, the effects of the finite bandwidth on the images obtained from radio-interferometrical observations, especially the inevitable effect called bandwidth smearing or chromatic aberration, will be investigated in this section, following the textbook of Taylor et al. (1999).
, the higher the sensitivity. However, using a large bandwidth is problematic, since the Fourier relation between brightness distribution and visibility is only valid for monochromatic signals. Therefore, the effects of the finite bandwidth on the images obtained from radio-interferometrical observations, especially the inevitable effect called bandwidth smearing or chromatic aberration, will be investigated in this section, following the textbook of Taylor et al. (1999).
For a single observing frequency 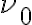 the brightness distribution is given by
the brightness distribution is given by
in which the "~" indicates the influence of a bandpass. The frequency-independent coordinates 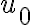 and
and 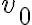 are given by
are given by
where 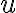 and
and 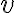 are the actual spatial coordinates of the visibility at the frequency
are the actual spatial coordinates of the visibility at the frequency 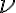 .
.
Therefore, using the generalized similarity theorem for Fourier transformations in 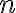 dimensions, which reads
dimensions, which reads
the two-dimensional Fourier relation between visibility and brightness distribution is given by
Furthermore, since the smeared visibility 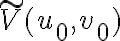 is obtained by rescaling and weighting the true visibility
is obtained by rescaling and weighting the true visibility 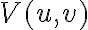 by a normalized bandpass function
by a normalized bandpass function 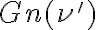 , where
, where 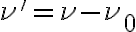 , and then integrating over the frequency band, another important effect must be taken into account. There will be a delay error of
, and then integrating over the frequency band, another important effect must be taken into account. There will be a delay error of
for signals arriving from a direction 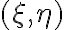 at frequency
at frequency 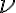 . Therefore, the phase is shifted by
. Therefore, the phase is shifted by
and the smeared visibility is given by
For simplicity, a point source with unit amplitude located at 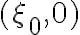 is assumed without restricting generality. Then, the true visibility is given by
is assumed without restricting generality. Then, the true visibility is given by
and the smeared visibility reads
Furthermore, assuming that the bandwidth is sufficiently small, so that 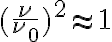 (in practice,
(in practice, 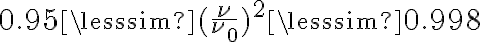 ), the bandwidth-smeared brightness distribution is given by
), the bandwidth-smeared brightness distribution is given by
using 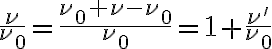 . Here, one can see that the term in squared brackets is the Fourier transform of the normalized bandpass function over
. Here, one can see that the term in squared brackets is the Fourier transform of the normalized bandpass function over 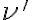 , to an argument
, to an argument 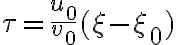 that represents a delay corresponding to the positional offset
that represents a delay corresponding to the positional offset 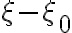 . Therefore, it is helpful to define a delay function
. Therefore, it is helpful to define a delay function 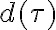 , given by
, given by
Using this delay function, the bandwidth-smeared brightness distribution then reads
Therefore, the bandwidth-smeared brightness distribution is the Fourier transform over 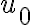 of the product of the true visibility with the delay function. Using the convolution theorem, the brightness distribution is given by
of the product of the true visibility with the delay function. Using the convolution theorem, the brightness distribution is given by
which is the convolution of the true image with a position-dependent bandwidth distortion function 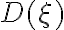 , which is the Fourier transform of the delay function
, which is the Fourier transform of the delay function
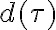 over
over 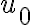 . Since this distortion function varies with the radial distance
. Since this distortion function varies with the radial distance 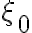 from the phase center and is always oriented along the radius to the phase center, the final image of an extended source can be interpreted as a radially-dependent convolution.
from the phase center and is always oriented along the radius to the phase center, the final image of an extended source can be interpreted as a radially-dependent convolution.
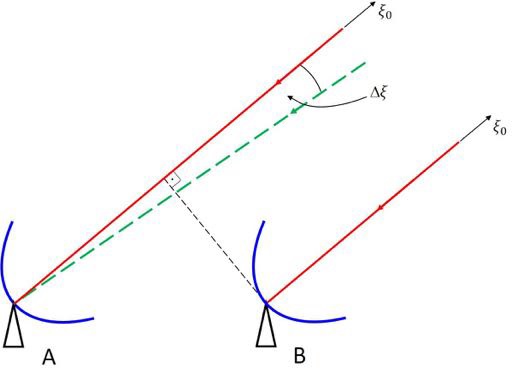
The effect of finite bandwidth is illustrated in Fig. 2.30. Here it is assumed that the observed emission of a source at position 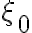 positively interferes exactly at frequency
positively interferes exactly at frequency 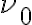 . A signal from a neighboring position shifted by
. A signal from a neighboring position shifted by 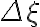 with respect to
with respect to 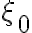 measured by one telescope at a frequency deviating from
measured by one telescope at a frequency deviating from 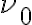 by an amount of
by an amount of 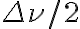 , for example, can then also produce maximum interference with a signal from
, for example, can then also produce maximum interference with a signal from 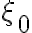 measured by the other telescope at frequency
measured by the other telescope at frequency 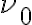 , if the delay difference matches. Therefore, a source observed with finite bandwidth can also produce structures away from its nominal position.
, if the delay difference matches. Therefore, a source observed with finite bandwidth can also produce structures away from its nominal position.
This finite bandwidth effect cannot be removed, because it is described by a mathematical functional. However, there are two methods to minimize the effects of bandwidth smearing. The first method is to limit the field size by dividing the observed area into subfields and produce separate images for all such subfields. To cover the complete area, the images of the subfields can then be fitted together. This technique is called mosaicing. The second method is to split the full frequency band into narrower sections, which will be summed up after imaging each individual data set. This method is called bandwidth synthesis.

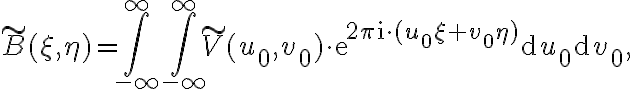
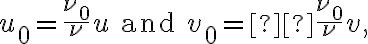
![\displaystyle \mathcal{FT}^n[f(\alpha\vec{x})] = \frac{1}{|\alpha|^n}\cdot F\left(\frac{\vec{s}}{\alpha}\right)\text{,} \displaystyle \mathcal{FT}^n[f(\alpha\vec{x})] = \frac{1}{|\alpha|^n}\cdot F\left(\frac{\vec{s}}{\alpha}\right)\text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/2a07d6755df3f8f9491bf87c0848d26b.gif)
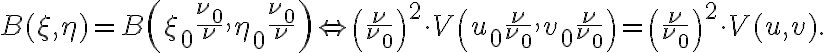
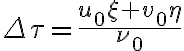
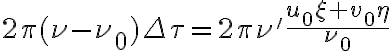
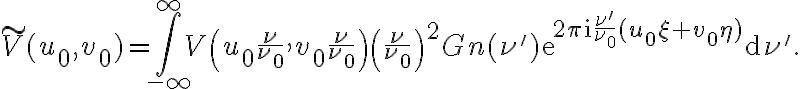
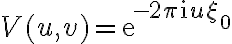
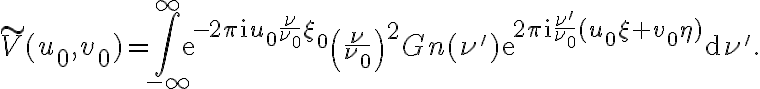
![\displaystyle \begin{array}{rl} \tilde{B}(\xi,\eta) & =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\frac{\nu}{\nu_0}\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\left(1+\frac{\nu'}{\nu_0}\right)\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\text{e}^{2\pi\text{i}u_0(\xi-\xi_0)}\left[\int_{-\infty}^{\infty}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}(\xi-\xi_0)}\text{d}\nu'\right]\text{d}u_0\delta(\eta)\text{,} \end{array} \displaystyle \begin{array}{rl} \tilde{B}(\xi,\eta) & =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\frac{\nu}{\nu_0}\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\left(1+\frac{\nu'}{\nu_0}\right)\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\text{e}^{2\pi\text{i}u_0(\xi-\xi_0)}\left[\int_{-\infty}^{\infty}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}(\xi-\xi_0)}\text{d}\nu'\right]\text{d}u_0\delta(\eta)\text{,} \end{array}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/fad18f927e16c8b02e3b961d3822a48e.gif)