Lecture - Fundamental Concepts
| Site: | WueCampus |
| Kurs: | vhb : Radio-Astronomical Interferometry (DEMO) |
| Kitap: | Lecture - Fundamental Concepts |
| Tarafından basılmıştır: | Gästanvändare |
| Tarih: | Cumartesi, 6 Aralık 2025, 7:41 AM |
1. Fourier optics
Learning Objectives:
- Basic concepts applied to telescopes
- Fourier and convolution mathematics
- Application of telescopes as spatial filters
2. Interferometry
Learning Objectives:
- Interferometry basics and concepts
- Application in radio astronomy
- Introduction to important values like visibility function and bandwidth
- Influences of the instrument set up to the measured values
- Orientation of pointing in the scope of coordinates
4. Receiver Response
Learning Objectives:
- Process and advantages of heterodyne frequency conversion
- Sensitivity of a radio-interferometrical array
- Effects of sampling, weighting and gridding
- Effect of finite bandwidth, bandwidth smearing
- Calibration of radio-interferometrical observations
4.1. Heterodyne frequency conversion
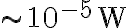 to work in the quadratic regime. The power
to work in the quadratic regime. The power 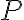 of the weak radio-astronomical signals entering the receiver is given by
of the weak radio-astronomical signals entering the receiver is given by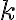 is the Boltzmann constant and
is the Boltzmann constant and 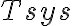 is the system temperature containing the receiver noise temperature and the antenna temperature. The antenna temperature is composed of the desired astronomical signal, a contribution from the earth's atmosphere, and possibly radiation from the ground. Due to that always present background the best case for the systemtemperature is
is the system temperature containing the receiver noise temperature and the antenna temperature. The antenna temperature is composed of the desired astronomical signal, a contribution from the earth's atmosphere, and possibly radiation from the ground. Due to that always present background the best case for the systemtemperature is 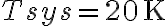 . Therefore, using a typical bandwidth of
. Therefore, using a typical bandwidth of 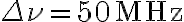 , the input power
, the input power 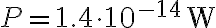 , meaning that the signal must be amplified by a factor of
, meaning that the signal must be amplified by a factor of 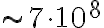 . However, amplification with such high factors is problematic, since the amplifying system becomes unstable due to feedback. A small amount of the power passing through the individual electronic components leaks out and reaches previous receiver elements, where it is again amplified. To circumvent this problem, the frequency of the signal
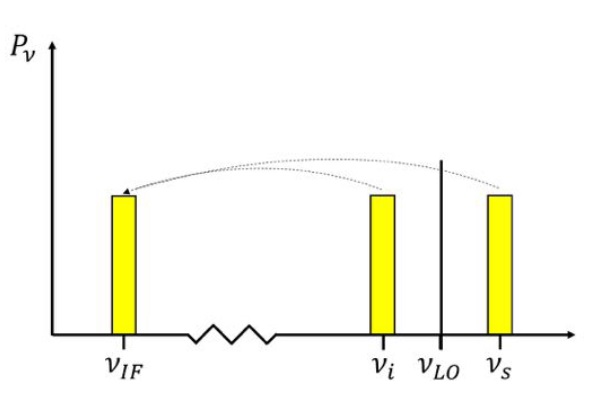
. However, amplification with such high factors is problematic, since the amplifying system becomes unstable due to feedback. A small amount of the power passing through the individual electronic components leaks out and reaches previous receiver elements, where it is again amplified. To circumvent this problem, the frequency of the signal 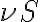 is down-converted to the lower intermediate frequency (IF) by mixing the signal with that of a local oscillator (LO), which decouples the signal path after the first amplification. This process is called heterodyne amplification or heterodyne frequency conversion.
is down-converted to the lower intermediate frequency (IF) by mixing the signal with that of a local oscillator (LO), which decouples the signal path after the first amplification. This process is called heterodyne amplification or heterodyne frequency conversion.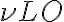 , close to the observing frequency
, close to the observing frequency 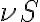 . To mix these two input signals, a semi-conductor diode with a non-linear current-voltage characteristic is used. The current-voltage relation of this diode can be written in terms of a Taylor expansion as
. To mix these two input signals, a semi-conductor diode with a non-linear current-voltage characteristic is used. The current-voltage relation of this diode can be written in terms of a Taylor expansion as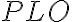 of higher harmonics decreases as
of higher harmonics decreases as 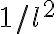 and usually the signal power
and usually the signal power 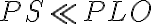 , only three terms of this frequency spectrum are important, namely:
, only three terms of this frequency spectrum are important, namely: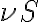 . Combining these terms, one obtains two high frequency (HF) bands that have equidistant separations from
. Combining these terms, one obtains two high frequency (HF) bands that have equidistant separations from 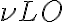 which correspond to the IF. For
which correspond to the IF. For 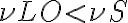 , these two HF bands correspond to the observing frequency, or signal frequency,
, these two HF bands correspond to the observing frequency, or signal frequency, 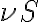 , and the image frequency
, and the image frequency 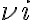 , and are denoted by
, and are denoted by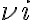 and
and 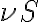 are called lower sideband (LSB) and upper sideband (USB), respectively. If both sidebands are used, the receiver operates in the so-called double-sideband mode. Otherwise, the receiver is said to operate in the single-sideband mode. To make sure that only the two HF bands are produced by the mixing process, an IF filter is used after the mixer to suppress all unwanted products of the mixing process (e.g.
are called lower sideband (LSB) and upper sideband (USB), respectively. If both sidebands are used, the receiver operates in the so-called double-sideband mode. Otherwise, the receiver is said to operate in the single-sideband mode. To make sure that only the two HF bands are produced by the mixing process, an IF filter is used after the mixer to suppress all unwanted products of the mixing process (e.g. 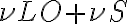 ).
).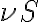 without changing any components following the mixer, which is essential for spectral-line measurements.
without changing any components following the mixer, which is essential for spectral-line measurements.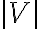 and
and 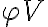 are the amplitude and phase of the complex visibility function,
are the amplitude and phase of the complex visibility function, 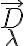 is the baseline between the two antennas in units of the observing wavelength and
is the baseline between the two antennas in units of the observing wavelength and 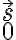 denotes the position of the observed radio source.
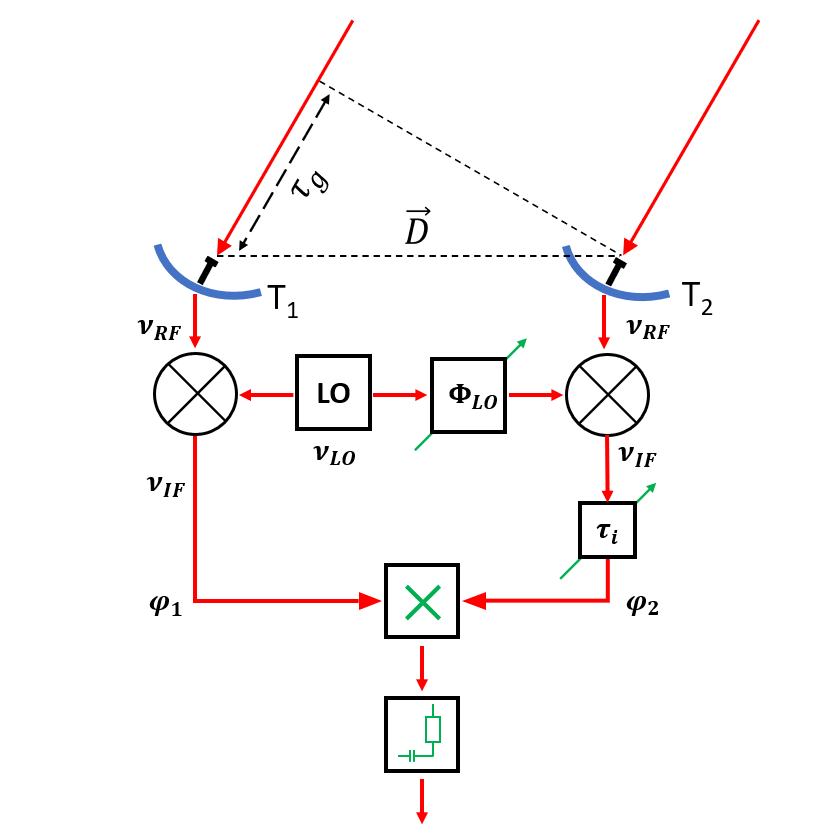
denotes the position of the observed radio source.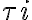 is introduced in one of the two branches of the receiver systems before the correlator. Second, a common LO signal is introduced into both mixers, with a phase shifter fed into one of the branches. Therefore, the resulting signal frequency
is introduced in one of the two branches of the receiver systems before the correlator. Second, a common LO signal is introduced into both mixers, with a phase shifter fed into one of the branches. Therefore, the resulting signal frequency 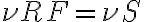 is given by
is given by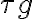 is the geometric time delay and
is the geometric time delay and 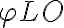 is the phase difference between the LO signals at the input of the mixers. The correlated power of such an interferometer can then be determined by changing the phase
is the phase difference between the LO signals at the input of the mixers. The correlated power of such an interferometer can then be determined by changing the phase 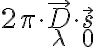 by
by  , leading to
, leading to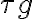 can be compensated by introducing an intrinsic time lag
can be compensated by introducing an intrinsic time lag 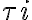 and that any phase variations due to the varying
and that any phase variations due to the varying 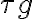 can be compensated by controlling
can be compensated by controlling 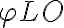 .
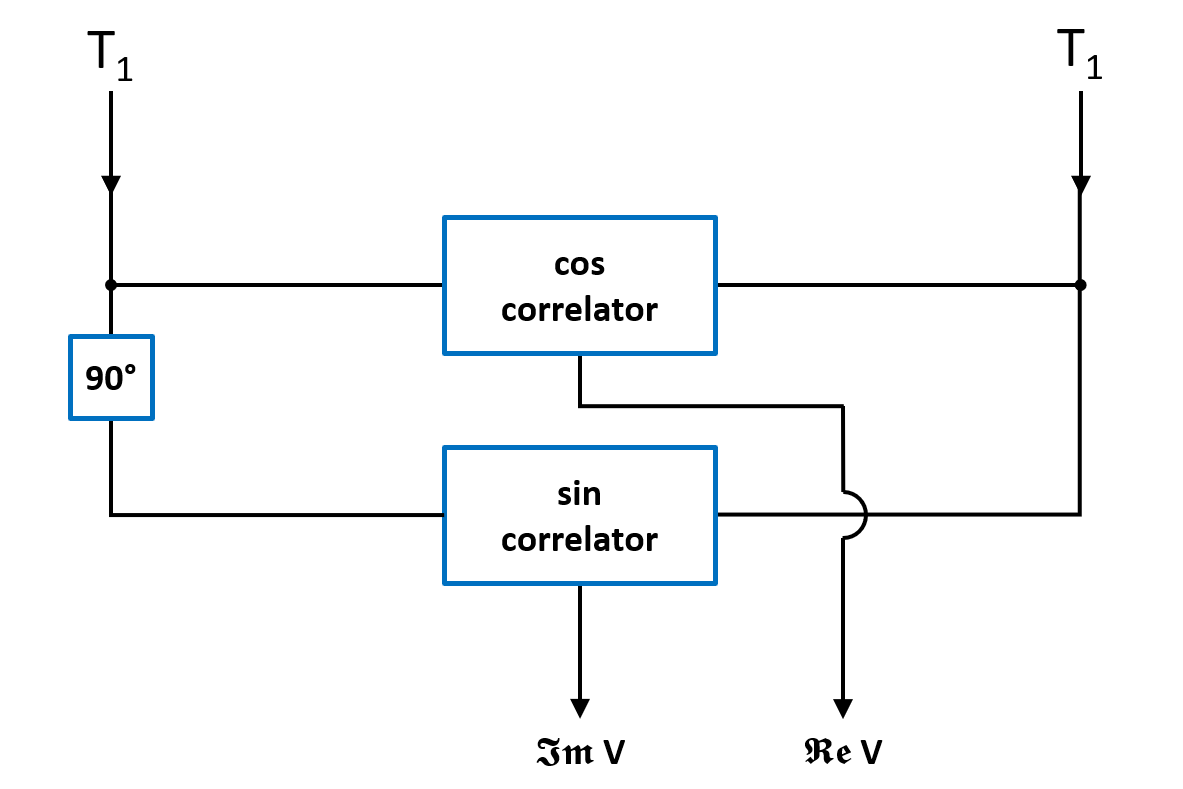
. 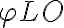 , the fringe frequency at which the interference pattern changes for each telescope pair due to the varying hour angle can be reduced. This is called fringe rotation. Looking at the time derivative of
, the fringe frequency at which the interference pattern changes for each telescope pair due to the varying hour angle can be reduced. This is called fringe rotation. Looking at the time derivative of  , given by
, given by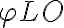 at a speed that is identical to the so-called natural fringe frequency, given by the term
at a speed that is identical to the so-called natural fringe frequency, given by the term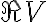 , and one that has a
, and one that has a 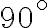 -phase shift in one of its branches prior to the correlation, leading to a sinusoidal output signal that corresponds to the imaginary part of the visibility
-phase shift in one of its branches prior to the correlation, leading to a sinusoidal output signal that corresponds to the imaginary part of the visibility 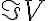 . With these output signals, the amplitude
. With these output signals, the amplitude 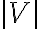 and phase
and phase 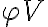 of the visibility can be calculated by
of the visibility can be calculated by4.2. Interferometer sensitivity
In order to estimate whether a source can be detected by a radio telescope or array, the so-called signal-to-noise ratio (SNR) has to be calculated. For a single telescope the signal is given by the measured antenna temperature 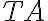 and the noise is given by the radiometer equation
and the noise is given by the radiometer equation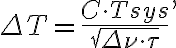
in which 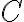 is a dimensionless constant depending on the receiver system used,
is a dimensionless constant depending on the receiver system used, 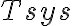 is the system temperature,
is the system temperature, 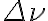 is the bandwidth of the receiver equipment and
is the bandwidth of the receiver equipment and 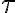 is the integration time.
is the integration time.
In radio interferometry, the signal is given by the brightness distribution 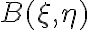 of a source that must be calculated by the Fourier integral of the measured visibility
of a source that must be calculated by the Fourier integral of the measured visibility 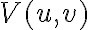 :
: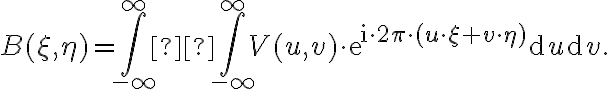
Therefore, to calculate the SNR in radio interferometry, one has to calculate the uncertainty of the brightness distribution 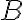 from the uncertainty of the complex visibility
from the uncertainty of the complex visibility 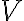 . As in every measurement, the measured data need to be sampled, meaning that the visibility is only measured at discrete locations
. As in every measurement, the measured data need to be sampled, meaning that the visibility is only measured at discrete locations 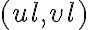 along the tracks in the
along the tracks in the 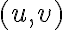 -plane. Let:
-plane. Let: 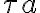 be the integration time of the individual samples in the
be the integration time of the individual samples in the 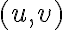 -plane,
-plane, 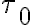 be the total integration time and
be the total integration time and 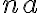 be the total number of antennas. Then the total number of measured visibilities
be the total number of antennas. Then the total number of measured visibilities 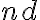 is given by
is given by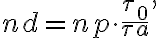
in which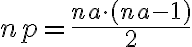
is the number of antenna pairs or rather the number of individual two-element interferometers. Since this brightness distribution suffers from incomplete 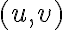 -coverage, the resulting image is called a "dirty image", which is also indicated by the superscript "D" of the brightness distribution
-coverage, the resulting image is called a "dirty image", which is also indicated by the superscript "D" of the brightness distribution 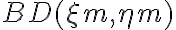 . The visibilities are measured at discrete locations
. The visibilities are measured at discrete locations 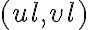 , so the brightness distribution is given by the discrete Fourier transform
, so the brightness distribution is given by the discrete Fourier transform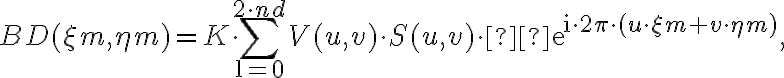
in which 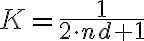 is a normalization constant and
is a normalization constant and 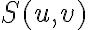 is a sampling function which is given by
is a sampling function which is given by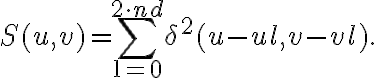
This sampling function is only non-zero where the visibility is measured in the 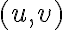 -plane.
-plane.
To suppress sidelobes, the beam shape of the observing array can be controlled by applying appropriate weights to the measured visibilities. Furthermore, if the observing array consists of telescopes that have different collecting areas 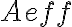 , and different receivers with different system temperatures
, and different receivers with different system temperatures 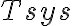 , frequency bandwidths
, frequency bandwidths 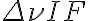 and integration times
and integration times 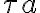 , one can also apply weights to control these differences. The weights can be written as
, one can also apply weights to control these differences. The weights can be written as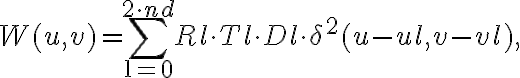
in which 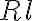 accounts for different telescope properties,
accounts for different telescope properties, 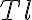 is a taper which controls the beam shape and
is a taper which controls the beam shape and 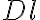 weights the density of the measured visibilities (more detailed information on the weights, especially on the
weights the density of the measured visibilities (more detailed information on the weights, especially on the 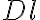 -factor, will be given in the next section 2.4.3). With these weights, the brightness distribution can then be written as
-factor, will be given in the next section 2.4.3). With these weights, the brightness distribution can then be written as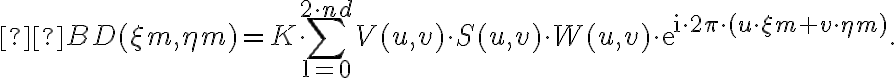
Because there is no measurement in the center of the 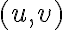 -plane, the
-plane, the 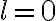 terms of the dirty image
terms of the dirty image 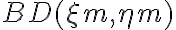 vanish, leading to
vanish, leading to![\displaystyle \begin{array}{rl} B^\text{D}(\xi_\text{m}, \eta_\text{m}) & = K \cdot \sum_{\text{l}=0}^{2\cdot n_\text{d}} V_\text{l} \cdot W_\text{l} \cdot \text{e}^{\text{i}\cdot 2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})} \\ & = 2 \cdot K \cdot \sum_{\text{l}=1}^{n_\text{d}} W_\text{l} \cdot [ \Re V_\text{l} \cdot \cos(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})) - \Im V_\text{l} \cdot \sin(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m}))] \text{,} \end{array} \displaystyle \begin{array}{rl} B^\text{D}(\xi_\text{m}, \eta_\text{m}) & = K \cdot \sum_{\text{l}=0}^{2\cdot n_\text{d}} V_\text{l} \cdot W_\text{l} \cdot \text{e}^{\text{i}\cdot 2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})} \\ & = 2 \cdot K \cdot \sum_{\text{l}=1}^{n_\text{d}} W_\text{l} \cdot [ \Re V_\text{l} \cdot \cos(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})) - \Im V_\text{l} \cdot \sin(2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m}))] \text{,} \end{array}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/04c07eca8079ad16147719b4c40cf6be.gif)
in which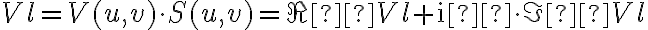
and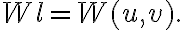
Note that the two additional terms ![\Re V_\text{l} \cdot \sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] \Re V_\text{l} \cdot \sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/50a8ee2bb161b4b41f5ab85faa62b859.gif) and
and ![\Im V_\text{l} \cdot \cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] \Im V_\text{l} \cdot \cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/30bd73fb80f7725027d8515833593296.gif) vanish under the integral of
vanish under the integral of 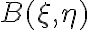 and can therefore also be neglected for the sum of
and can therefore also be neglected for the sum of 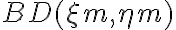 .
.
To calculate the sensitivity in the image plane, a point source at the phase and image center is considered. For such a point source, the visibility 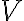 is real and constant across the entire
is real and constant across the entire 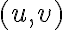 -plane and only varies due to random noise. Furthermore, because
-plane and only varies due to random noise. Furthermore, because 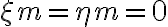 , the
, the ![\sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] \sin[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/9b252b33edecca4b4f2300bbdd905d3b.gif) -term vanishes and
-term vanishes and ![\cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] = 1 \cos[2\pi \cdot (u_\text{l} \cdot \xi_\text{m} + v_\text{l} \cdot \eta_\text{m})] = 1](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/423a918ff62e58d89f2ee83a7f9b4ea6.gif) . Therefore, the dirty image of such a point source is given by
. Therefore, the dirty image of such a point source is given by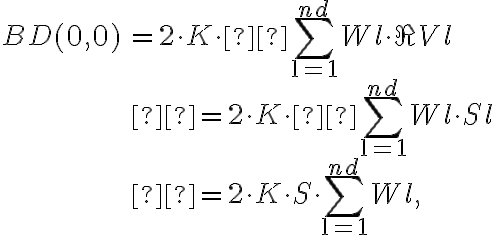
in which 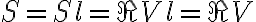 is the total flux density of the source. Note that here
is the total flux density of the source. Note that here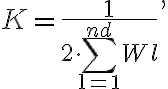
so that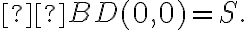
Assuming that the uncertainty of the flux density 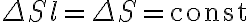 , the noise in the dirty image is given by
, the noise in the dirty image is given by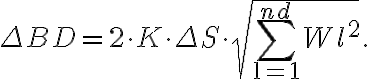
Furthermore, assuming an observing array that consists of 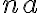 identical telescopes
identical telescopes 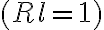 and a naturally weighted
and a naturally weighted 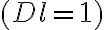 , untapered
, untapered 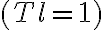 image,
image, 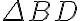 simplifies to
simplifies to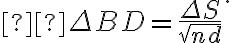
Since 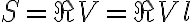 , the uncertainty of the flux density
, the uncertainty of the flux density 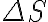 is given by the rms noise
is given by the rms noise 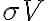 of the measured visibilities which is, based on the radiometer equation, given by
of the measured visibilities which is, based on the radiometer equation, given by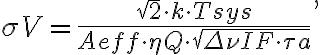
in which 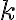 is the Boltzmann constant and
is the Boltzmann constant and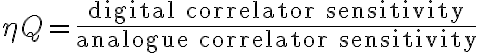
is the quantization efficiency accounting for the quantization noise due to the conversion of analogue signals to digital signals.
Inserting 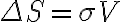 into
into 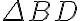 , the sensitivity for the synthesized image is finally given by
, the sensitivity for the synthesized image is finally given by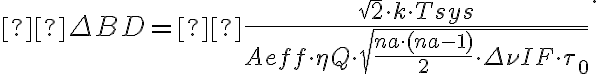
4.3. Sampling, weighting, gridding
Sampling
As previously mentioned, the visibilities are only measured at discrete locations 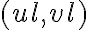 . Therefore, the measured visibilities are given by the multiplication of the true visibility function
. Therefore, the measured visibilities are given by the multiplication of the true visibility function 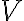 and a sampling function
and a sampling function 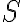 . Hence, the dirty image
. Hence, the dirty image 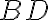 is then given by the convolution of their Fourier transforms:
is then given by the convolution of their Fourier transforms:
in which ![\mathcal{FT}[x] \mathcal{FT}[x]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/290d52c31264c1e54193648e665e8ad5.gif) denotes the Fourier transform of
denotes the Fourier transform of 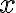 and the double-star
and the double-star 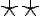 indicates a two-dimensional convolution.
indicates a two-dimensional convolution.
Weighting
Furthermore, as also previously mentioned, the visibilities can be weighted by multiplying a weighting function 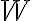 to the visibilities
to the visibilities 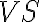 :
:
This weighting function 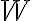 consists of three individual factors:
consists of three individual factors:
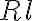 accounts for different telescope properties within an array (e.g. different
accounts for different telescope properties within an array (e.g. different 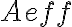 ,
, 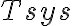 ,
, 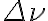 and
and 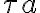 ),
),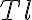 is a taper that controls the beam shape,
is a taper that controls the beam shape,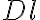 weights the density of the measured visibilities.
weights the density of the measured visibilities.
The 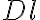 -factor affects the angular resolution and sensitivity of the array. On the one hand side, the highest angular resolution can be achieved by weighting the visibilities as if they had been measured uniformly over the entire
-factor affects the angular resolution and sensitivity of the array. On the one hand side, the highest angular resolution can be achieved by weighting the visibilities as if they had been measured uniformly over the entire 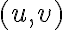 -plane. Therefore, this weighting scheme is called uniform weighting. Since the density of the measured visibilities is higher at the center of the
-plane. Therefore, this weighting scheme is called uniform weighting. Since the density of the measured visibilities is higher at the center of the 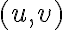 -plane, the visibilities in the outer part are over-weighted leading to the highest angular resolution. On the other hand, the highest sensitivity is achieved if all measured visibilities are weighted by identical weights. This weighting scheme is called natural weighting. The main properties of both schemes are summarized in the following:
-plane, the visibilities in the outer part are over-weighted leading to the highest angular resolution. On the other hand, the highest sensitivity is achieved if all measured visibilities are weighted by identical weights. This weighting scheme is called natural weighting. The main properties of both schemes are summarized in the following:
- uniform weighting:
With this weighting function 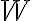 , the dirty image
, the dirty image 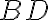 is given by
is given by
![\displaystyle B^\text{D} = \mathcal{FT}[V^\text{W}] = \mathcal{FT}[W \cdot V^\text{S}] = \mathcal{FT}[W] \star \star \mathcal{FT}[V^\text{S}] = \mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S]) \text{.} \displaystyle B^\text{D} = \mathcal{FT}[V^\text{W}] = \mathcal{FT}[W \cdot V^\text{S}] = \mathcal{FT}[W] \star \star \mathcal{FT}[V^\text{S}] = \mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S]) \text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/2eca0fb08d98b8eadba80a378194ca7b.gif)
Gridding
To use the time advantage of the fast Fourier transform (FFT) algorithm, the visibilities must be interpolated onto a regular grid of size 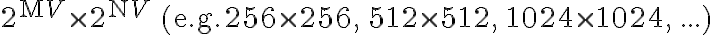 , resulting in an image of size
, resulting in an image of size 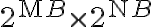 . This interpolation, also called gridding, is done at first by convolving the weighted discrete visibility
. This interpolation, also called gridding, is done at first by convolving the weighted discrete visibility 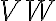 with an appropriate function
with an appropriate function 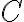 to obtain a continuous visibility distribution. This continuous visibility distribution is then resampled at points of the regular grid with spacings
to obtain a continuous visibility distribution. This continuous visibility distribution is then resampled at points of the regular grid with spacings 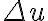 and
and 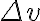 by multiplying a two-dimensional Shah-function
by multiplying a two-dimensional Shah-function 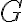 , given by
, given by
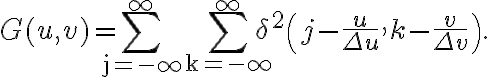
After these modifications, the visibility 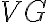 is given by
is given by ![\displaystyle V^\text{G} = G \cdot (C \star \star V^\text{W}) = G \cdot [C \star \star (W \cdot V^\text{S})] = G \cdot [C \star \star (W \cdot V \cdot S)] \displaystyle V^\text{G} = G \cdot (C \star \star V^\text{W}) = G \cdot [C \star \star (W \cdot V^\text{S})] = G \cdot [C \star \star (W \cdot V \cdot S)]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/24e98dae931507ec8c75522931b13c87.gif)
and the dirty image 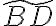 reads
reads![\displaystyle \tilde{B^\text{D}} = \mathcal{FT}[G] \star \star (\mathcal{FT}[C] \cdot \mathcal{FT}[V^\text{W}]) = \mathcal{FT}[G] \star \star \{ \mathcal{FT}[C] \cdot [\mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S])]\} \text{.} \displaystyle \tilde{B^\text{D}} = \mathcal{FT}[G] \star \star (\mathcal{FT}[C] \cdot \mathcal{FT}[V^\text{W}]) = \mathcal{FT}[G] \star \star \{ \mathcal{FT}[C] \cdot [\mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S])]\} \text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/1b44c8e537f9f7143cf62d73d416bec3.gif)
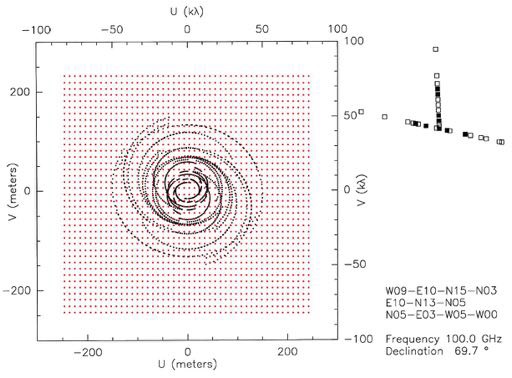
This gridding process is illustrated in the Fig. 2.29, in which real 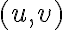 -tracks measured by the IRAM interferometer at Plateau de Bure in France are shown as black dotted ellipses. Furthermore, a regular grid, onto which the visibilities have been interpolated, is shown as red dots.
-tracks measured by the IRAM interferometer at Plateau de Bure in France are shown as black dotted ellipses. Furthermore, a regular grid, onto which the visibilities have been interpolated, is shown as red dots.
Since the sampling intervals 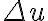 and
and 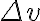 in the
in the 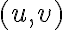 -plane are inversely proportional to the sampling intervals
-plane are inversely proportional to the sampling intervals 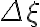 and
and 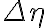 in the image plane (
in the image plane ( 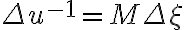 and
and 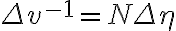 for a grid of size
for a grid of size 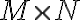 ), the maximum map size in one domain is given by the minimum sampling interval in the other. Therefore, it is important to choose appropriate sampling intervals
), the maximum map size in one domain is given by the minimum sampling interval in the other. Therefore, it is important to choose appropriate sampling intervals 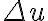 and
and 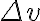 . If
. If 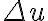 and
and 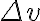 are chosen to be too large for example, this will result in artefacts in the image plane produced by reflections of structures from the map edges, which is called aliasing.
are chosen to be too large for example, this will result in artefacts in the image plane produced by reflections of structures from the map edges, which is called aliasing.
The most effective way to deal with this aliasing is to use a convolution function 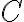 for which the Fourier transform in the image plane
for which the Fourier transform in the image plane ![\mathcal{FT}[C] \mathcal{FT}[C]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/7265b9d7b7857f89d7fdad5bc301eb5a.gif) decreases rapidly at the image edges and is nearly constant over the image. Therefore, the simplest choice for the convolution function
decreases rapidly at the image edges and is nearly constant over the image. Therefore, the simplest choice for the convolution function 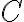 is a rectangular function, but with this choice the aliasing would be strongest. A better choice would be a sinc function, however a Gaussian-sinc function (product of a Gaussian and a sinc function) leads to the best suppression of aliasing.
is a rectangular function, but with this choice the aliasing would be strongest. A better choice would be a sinc function, however a Gaussian-sinc function (product of a Gaussian and a sinc function) leads to the best suppression of aliasing.
Finally, the gridding modifications must be corrected after the Fourier transform by dividing the dirty image 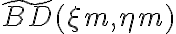 by the inverse Fourier transform of the gridding convolution function
by the inverse Fourier transform of the gridding convolution function 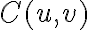 . Therefore, the so-called grid-corrected image
. Therefore, the so-called grid-corrected image 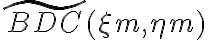 is given by
is given by} \text{.} \displaystyle \tilde{B^\text{D}_\text{C}}(\xi_\text{m},\eta_\text{m}) = \frac{\tilde{B^\text{D}}(\xi_\text{m},\eta_\text{m})}{\mathcal{FT}[C](u,v)} \text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/38a39a2ff58598a9e9090adcf122a3df.gif)
4.4. Bandwidth smearing
As already seen in Chapt. 2 Sect. 4.2, the sensitivity of radio-interferometrical measurements depends on the effective area of the telescopes 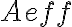 and the bandwidth
and the bandwidth 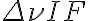 . The larger
. The larger 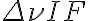 , the higher the sensitivity. However, using a large bandwidth is problematic, since the Fourier relation between brightness distribution and visibility is only valid for monochromatic signals. Therefore, the effects of the finite bandwidth on the images obtained from radio-interferometrical observations, especially the inevitable effect called bandwidth smearing or chromatic aberration, will be investigated in this section, following the textbook of Taylor et al. (1999).
, the higher the sensitivity. However, using a large bandwidth is problematic, since the Fourier relation between brightness distribution and visibility is only valid for monochromatic signals. Therefore, the effects of the finite bandwidth on the images obtained from radio-interferometrical observations, especially the inevitable effect called bandwidth smearing or chromatic aberration, will be investigated in this section, following the textbook of Taylor et al. (1999).
For a single observing frequency 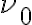 the brightness distribution is given by
the brightness distribution is given by
in which the "~" indicates the influence of a bandpass. The frequency-independent coordinates 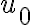 and
and 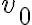 are given by
are given by
where 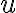 and
and 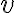 are the actual spatial coordinates of the visibility at the frequency
are the actual spatial coordinates of the visibility at the frequency 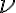 .
.
Therefore, using the generalized similarity theorem for Fourier transformations in 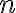 dimensions, which reads
dimensions, which reads
the two-dimensional Fourier relation between visibility and brightness distribution is given by
Furthermore, since the smeared visibility 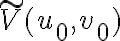 is obtained by rescaling and weighting the true visibility
is obtained by rescaling and weighting the true visibility 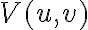 by a normalized bandpass function
by a normalized bandpass function 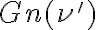 , where
, where 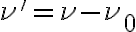 , and then integrating over the frequency band, another important effect must be taken into account. There will be a delay error of
, and then integrating over the frequency band, another important effect must be taken into account. There will be a delay error of
for signals arriving from a direction 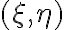 at frequency
at frequency 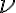 . Therefore, the phase is shifted by
. Therefore, the phase is shifted by
and the smeared visibility is given by
For simplicity, a point source with unit amplitude located at 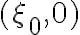 is assumed without restricting generality. Then, the true visibility is given by
is assumed without restricting generality. Then, the true visibility is given by
and the smeared visibility reads
Furthermore, assuming that the bandwidth is sufficiently small, so that 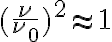 (in practice,
(in practice, 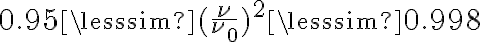 ), the bandwidth-smeared brightness distribution is given by
), the bandwidth-smeared brightness distribution is given by
using 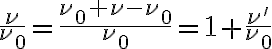 . Here, one can see that the term in squared brackets is the Fourier transform of the normalized bandpass function over
. Here, one can see that the term in squared brackets is the Fourier transform of the normalized bandpass function over 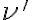 , to an argument
, to an argument 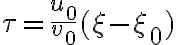 that represents a delay corresponding to the positional offset
that represents a delay corresponding to the positional offset 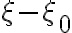 . Therefore, it is helpful to define a delay function
. Therefore, it is helpful to define a delay function 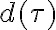 , given by
, given by
Using this delay function, the bandwidth-smeared brightness distribution then reads
Therefore, the bandwidth-smeared brightness distribution is the Fourier transform over 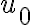 of the product of the true visibility with the delay function. Using the convolution theorem, the brightness distribution is given by
of the product of the true visibility with the delay function. Using the convolution theorem, the brightness distribution is given by
which is the convolution of the true image with a position-dependent bandwidth distortion function 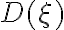 , which is the Fourier transform of the delay function
, which is the Fourier transform of the delay function
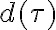 over
over 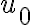 . Since this distortion function varies with the radial distance
. Since this distortion function varies with the radial distance 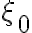 from the phase center and is always oriented along the radius to the phase center, the final image of an extended source can be interpreted as a radially-dependent convolution.
from the phase center and is always oriented along the radius to the phase center, the final image of an extended source can be interpreted as a radially-dependent convolution.
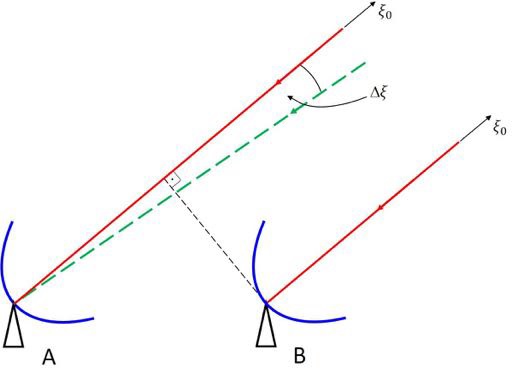
The effect of finite bandwidth is illustrated in Fig. 2.30. Here it is assumed that the observed emission of a source at position 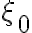 positively interferes exactly at frequency
positively interferes exactly at frequency 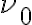 . A signal from a neighboring position shifted by
. A signal from a neighboring position shifted by 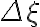 with respect to
with respect to 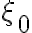 measured by one telescope at a frequency deviating from
measured by one telescope at a frequency deviating from 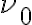 by an amount of
by an amount of 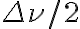 , for example, can then also produce maximum interference with a signal from
, for example, can then also produce maximum interference with a signal from 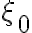 measured by the other telescope at frequency
measured by the other telescope at frequency 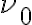 , if the delay difference matches. Therefore, a source observed with finite bandwidth can also produce structures away from its nominal position.
, if the delay difference matches. Therefore, a source observed with finite bandwidth can also produce structures away from its nominal position.
This finite bandwidth effect cannot be removed, because it is described by a mathematical functional. However, there are two methods to minimize the effects of bandwidth smearing. The first method is to limit the field size by dividing the observed area into subfields and produce separate images for all such subfields. To cover the complete area, the images of the subfields can then be fitted together. This technique is called mosaicing. The second method is to split the full frequency band into narrower sections, which will be summed up after imaging each individual data set. This method is called bandwidth synthesis.
4.5. Calibration
The true visibility of a target source 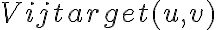 observed by two telescopes
observed by two telescopes 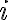 and
and 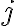 of an array is related to the observed visibility
of an array is related to the observed visibility 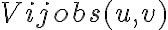 by
by
in which 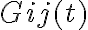 is the time-variable and complex gain factor of the correlation product of the two telescopes
is the time-variable and complex gain factor of the correlation product of the two telescopes 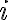 and
and 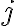 . This gain factor includes variations caused by different effects, e.g., weather effects, effects of the atmospheric paths to the telescopes, and instrumental effects. Therefore, to determine the true visibility, the gain factor has to be calculated. This can be done via frequent observations of calibrator sources with known flux densities
. This gain factor includes variations caused by different effects, e.g., weather effects, effects of the atmospheric paths to the telescopes, and instrumental effects. Therefore, to determine the true visibility, the gain factor has to be calculated. This can be done via frequent observations of calibrator sources with known flux densities 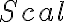 and accurately known positions. Furthermore, these sources have to be point sources, meaning that their angular size
and accurately known positions. Furthermore, these sources have to be point sources, meaning that their angular size 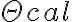 is
is
Then, the complex gain 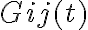 of each interferometer can be determined by
of each interferometer can be determined by
in which 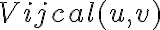 is the observed visibility of a calibrator source. This complex gain factor can then be used to calibrate the observed visibility of the target source. The true visibility of a target source
is the observed visibility of a calibrator source. This complex gain factor can then be used to calibrate the observed visibility of the target source. The true visibility of a target source 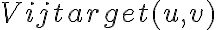 is then given by
is then given by
Note that the gains 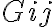 can also be expressed by the voltage gain factors
can also be expressed by the voltage gain factors 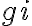 and
and 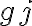 of the individual i-th and j-th antennas by
of the individual i-th and j-th antennas by
This reduces the amount of calibration data, since there are many more correlated antenna pairs than antennas in large arrays. Furthermore, this makes the calibration procedure more flexible, since, for example, a source that is resolved at the longest baselines of an array can be used to compute the gain factors of the individual antennas from measurements made only at shorter baselines, at which the source appears unresolved.
Gibb's phenomenon
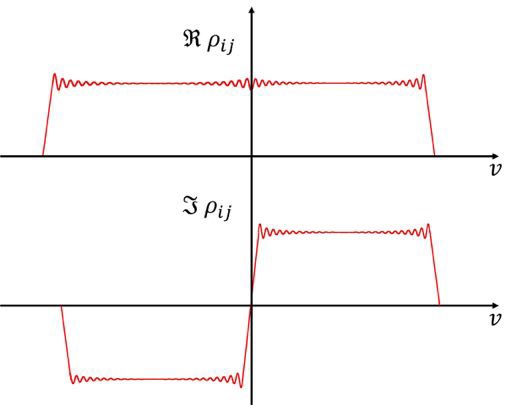 |
|---|
| Fig. 2.34 Real and imaginary part of a frequency power spectrum for an idealized rectangular bandpass. |
In continuum observations the correlation of the signals is usually measured for zero time lags, meaning that the correlation of the measured signal is averaged over the bandwidth, which is defined via a bandpass. In spectral line observations (see Chapt. 3 Sect. 4), measurements at different frequencies across the bandpass are required, which can be implemented by correlating the signals as a function of time lags. After Fourier transforming this correlation output, this yields the so-called cross power spectrum. This cross power spectrum is obtained for 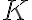 frequency channels (for more detailed information see Chapt. 3 Sect. 4).
frequency channels (for more detailed information see Chapt. 3 Sect. 4).
To calibrate an interferometer over the bandpass, which represents the filter characteristics of the last IF stage, a continuum point source is used to determine the complex gains of the interferometer, which yields the true cross-correlation spectrum of the observed target source. For calibrator sources with a constant continuum spectrum over the bandpass, the behavior of the complex gains 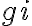 and
and 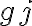 across the bandpass
across the bandpass 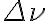 are given by the correlated power as a function of frequency for each interferometer of the observing array. The real and imaginary parts of this correlated power, measured for a continuum source with a flat spectrum, are shown in Fig. 2.31 for an idealized rectangular bandpass.
are given by the correlated power as a function of frequency for each interferometer of the observing array. The real and imaginary parts of this correlated power, measured for a continuum source with a flat spectrum, are shown in Fig. 2.31 for an idealized rectangular bandpass.
The observed visibility of an unknown target source is given by
in which 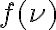 is the Fourier transform of the truncating function in the frequency domain, which is a sinc function given by
is the Fourier transform of the truncating function in the frequency domain, which is a sinc function given by
Here, 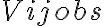 is given by a convolution with
is given by a convolution with 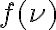 , since the cross-correlation has only a finite maximum lag of
, since the cross-correlation has only a finite maximum lag of 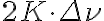 . The observed visibility
. The observed visibility 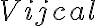 of a calibrator source with
of a calibrator source with 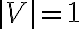 and
and 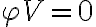 is then given by
is then given by
Finally, the true visibility 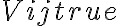 of the observed target source is given by
of the observed target source is given by
in which the gains do not cancel out, due to the convolution. Therefore, the original frequency power spectrum, shown in Fig. 2.31, is convolved with the sinc function 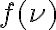 , due to the finite lag, which will lead to large errors, if the target source has a spectral line near
, due to the finite lag, which will lead to large errors, if the target source has a spectral line near 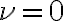 . This is known as Gibbs' phenomenon.
. This is known as Gibbs' phenomenon.
Since the cross-correlation function has a complex power spectrum, Gibbs' phenomenon has strong influence on the imaginary part of the true visibility, because of the ratio in the equation for 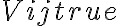 , which leads to non-negligible errors, especially for strong line emission near the step at
, which leads to non-negligible errors, especially for strong line emission near the step at 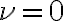 . Since the step in the imaginary part is large, these errors have a strong effect on the phases, producing strong ripples.
. Since the step in the imaginary part is large, these errors have a strong effect on the phases, producing strong ripples.
5. Image reconstruction
Learning Objectives:
- Image reconstruction using the CLEAN and MEM algorithms
- Image defects
- Image reconstruction using self-calibration
6. Digital Beamforming
Learning Objectives:
- Geometric understanding of an array performing beamforming
- Introduction and mathematical concept of weighting elements
- Mathematical description of one and two dimensional array factors
- Visualization of array factors, beam forming and beam steering
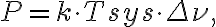
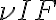
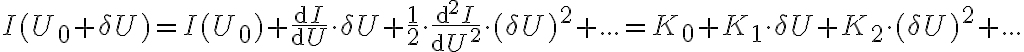
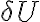
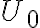
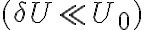
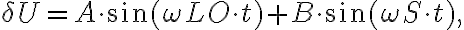
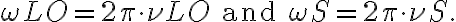
![\displaystyle \begin{array}{rl} I = & K_0 + K_1 \cdot \left[A \cdot \sin (\omega_\text{LO} \cdot t) + B \cdot \sin (\omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot \left[\frac{A^2}{2} + \frac{B^2}{2}\right] \\ & - K_2 \cdot \left[\frac{A^2}{2} \cdot \cos (2 \cdot \omega_\text{LO} \cdot t) + \frac{B^2}{2} \cdot \cos (2 \cdot \omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} - \omega_\text{S}) \cdot t\right] \\ & - K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} + \omega_\text{S}) \cdot t\right] \text{,} \end{array} \displaystyle \begin{array}{rl} I = & K_0 + K_1 \cdot \left[A \cdot \sin (\omega_\text{LO} \cdot t) + B \cdot \sin (\omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot \left[\frac{A^2}{2} + \frac{B^2}{2}\right] \\ & - K_2 \cdot \left[\frac{A^2}{2} \cdot \cos (2 \cdot \omega_\text{LO} \cdot t) + \frac{B^2}{2} \cdot \cos (2 \cdot \omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} - \omega_\text{S}) \cdot t\right] \\ & - K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} + \omega_\text{S}) \cdot t\right] \text{,} \end{array}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/592ca3c1f2371daedb504e40c89cc654.gif)
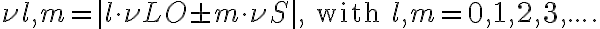
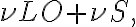
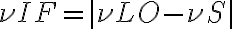
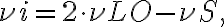
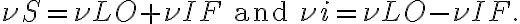
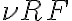
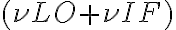
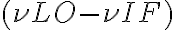
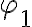
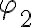
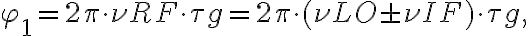
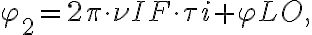
![\displaystyle P = A_0 \cdot \Delta \nu \cdot |V| \cdot \cos [2 \pi (\nu_\text{LO} \cdot \tau_\text{g} \pm \nu_\text{IF} \cdot \Delta \tau) - \varphi_\text{V} - \varphi_\text{LO}] \text{,} \displaystyle P = A_0 \cdot \Delta \nu \cdot |V| \cdot \cos [2 \pi (\nu_\text{LO} \cdot \tau_\text{g} \pm \nu_\text{IF} \cdot \Delta \tau) - \varphi_\text{V} - \varphi_\text{LO}] \text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/b0bdf3019af0affc0b3b21ed44cbc7bc.gif)
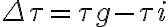
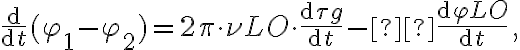
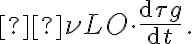
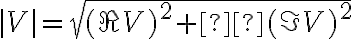
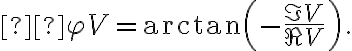
![\displaystyle B^\text{D} = \mathcal{FT}[V^\text{S}] = \mathcal{FT}[V \cdot S] = \mathcal{FT}[V] \star \star \mathcal{FT}[S] \text{,} \displaystyle B^\text{D} = \mathcal{FT}[V^\text{S}] = \mathcal{FT}[V \cdot S] = \mathcal{FT}[V] \star \star \mathcal{FT}[S] \text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/ae19d1b8e17a3ebbdd115e1eeff5e233.gif)
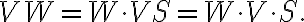
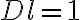
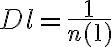
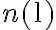
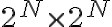
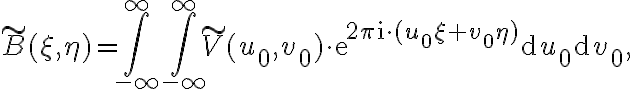
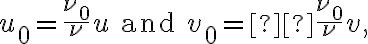
![\displaystyle \mathcal{FT}^n[f(\alpha\vec{x})] = \frac{1}{|\alpha|^n}\cdot F\left(\frac{\vec{s}}{\alpha}\right)\text{,} \displaystyle \mathcal{FT}^n[f(\alpha\vec{x})] = \frac{1}{|\alpha|^n}\cdot F\left(\frac{\vec{s}}{\alpha}\right)\text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/2a07d6755df3f8f9491bf87c0848d26b.gif)
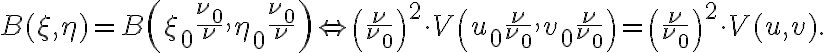
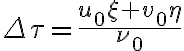
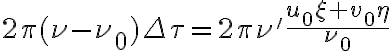
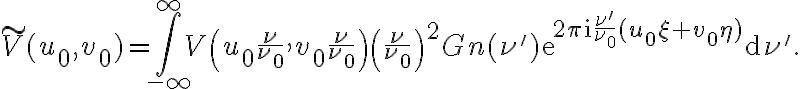
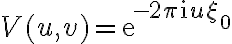
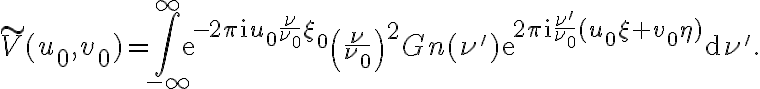
![\displaystyle \begin{array}{rl} \tilde{B}(\xi,\eta) & =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\frac{\nu}{\nu_0}\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\left(1+\frac{\nu'}{\nu_0}\right)\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\text{e}^{2\pi\text{i}u_0(\xi-\xi_0)}\left[\int_{-\infty}^{\infty}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}(\xi-\xi_0)}\text{d}\nu'\right]\text{d}u_0\delta(\eta)\text{,} \end{array} \displaystyle \begin{array}{rl} \tilde{B}(\xi,\eta) & =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\frac{\nu}{\nu_0}\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\left[\int_{-\infty}^{\infty}{e}^{-2\pi\text{i}u_0\left(1+\frac{\nu'}{\nu_0}\right)\xi_0}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}\xi}\text{d}\nu'\right]\text{e}^{2\pi\text{i}u_0\xi}\text{d}u_0\delta(\eta) \\
& =\int_{-\infty}^{\infty}\text{e}^{2\pi\text{i}u_0(\xi-\xi_0)}\left[\int_{-\infty}^{\infty}G_\text{n}(\nu')\text{e}^{2\pi\text{i}u_0\frac{\nu'}{\nu_0}(\xi-\xi_0)}\text{d}\nu'\right]\text{d}u_0\delta(\eta)\text{,} \end{array}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/fad18f927e16c8b02e3b961d3822a48e.gif)
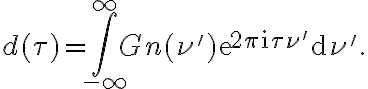
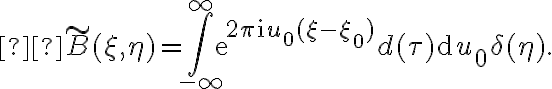
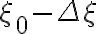
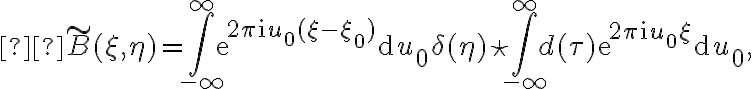
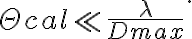
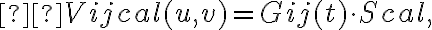
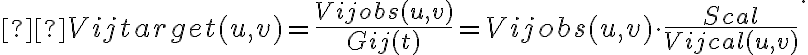
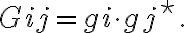
![\displaystyle V_\text{ij}^\text{obs}(\nu) = f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\cdot V(\nu)\right]\,\text{,} \displaystyle V_\text{ij}^\text{obs}(\nu) = f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\cdot V(\nu)\right]\,\text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/7297e6737b5dd7ac508e7e663b3eff7b.gif)
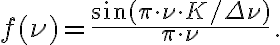
![\displaystyle V_\text{ij}^\text{cal}(\nu)= f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\right]\,\text{.} \displaystyle V_\text{ij}^\text{cal}(\nu)= f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\right]\,\text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/ae8aea962d1fb5efc776eeae15172263.gif)
![\displaystyle V_\text{ij}^\text{true}(\nu) = \frac{V_\text{ij}^\text{obs}(\nu)}{V_\text{ij}^\text{cal}(\nu)} = \frac{f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\cdot V(\nu)\right]}{f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\right]}\,\text{,} \displaystyle V_\text{ij}^\text{true}(\nu) = \frac{V_\text{ij}^\text{obs}(\nu)}{V_\text{ij}^\text{cal}(\nu)} = \frac{f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\cdot V(\nu)\right]}{f(\nu)\star\left[g_\text{i}(\nu)\cdot g_\text{j}^\star(\nu)\right]}\,\text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/a8f767a1bf856a6926838936f2d61110.gif)