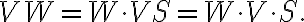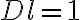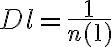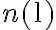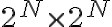Lecture - Fundamental Concepts
4. Receiver Response
4.3. Sampling, weighting, gridding
Sampling
As previously mentioned, the visibilities are only measured at discrete locations 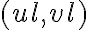 . Therefore, the measured visibilities are given by the multiplication of the true visibility function
. Therefore, the measured visibilities are given by the multiplication of the true visibility function 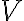 and a sampling function
and a sampling function 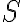 . Hence, the dirty image
. Hence, the dirty image 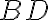 is then given by the convolution of their Fourier transforms:
is then given by the convolution of their Fourier transforms:
in which ![\mathcal{FT}[x] \mathcal{FT}[x]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/290d52c31264c1e54193648e665e8ad5.gif) denotes the Fourier transform of
denotes the Fourier transform of 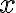 and the double-star
and the double-star 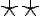 indicates a two-dimensional convolution.
indicates a two-dimensional convolution.
Weighting
Furthermore, as also previously mentioned, the visibilities can be weighted by multiplying a weighting function 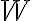 to the visibilities
to the visibilities 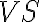 :
:
This weighting function 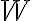 consists of three individual factors:
consists of three individual factors:
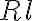 accounts for different telescope properties within an array (e.g. different
accounts for different telescope properties within an array (e.g. different 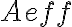 ,
, 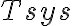 ,
, 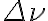 and
and 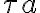 ),
),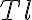 is a taper that controls the beam shape,
is a taper that controls the beam shape,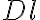 weights the density of the measured visibilities.
weights the density of the measured visibilities.
The 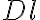 -factor affects the angular resolution and sensitivity of the array. On the one hand side, the highest angular resolution can be achieved by weighting the visibilities as if they had been measured uniformly over the entire
-factor affects the angular resolution and sensitivity of the array. On the one hand side, the highest angular resolution can be achieved by weighting the visibilities as if they had been measured uniformly over the entire 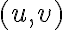 -plane. Therefore, this weighting scheme is called uniform weighting. Since the density of the measured visibilities is higher at the center of the
-plane. Therefore, this weighting scheme is called uniform weighting. Since the density of the measured visibilities is higher at the center of the 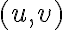 -plane, the visibilities in the outer part are over-weighted leading to the highest angular resolution. On the other hand, the highest sensitivity is achieved if all measured visibilities are weighted by identical weights. This weighting scheme is called natural weighting. The main properties of both schemes are summarized in the following:
-plane, the visibilities in the outer part are over-weighted leading to the highest angular resolution. On the other hand, the highest sensitivity is achieved if all measured visibilities are weighted by identical weights. This weighting scheme is called natural weighting. The main properties of both schemes are summarized in the following:
- uniform weighting:
With this weighting function 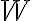 , the dirty image
, the dirty image 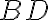 is given by
is given by
![\displaystyle B^\text{D} = \mathcal{FT}[V^\text{W}] = \mathcal{FT}[W \cdot V^\text{S}] = \mathcal{FT}[W] \star \star \mathcal{FT}[V^\text{S}] = \mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S]) \text{.} \displaystyle B^\text{D} = \mathcal{FT}[V^\text{W}] = \mathcal{FT}[W \cdot V^\text{S}] = \mathcal{FT}[W] \star \star \mathcal{FT}[V^\text{S}] = \mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S]) \text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/2eca0fb08d98b8eadba80a378194ca7b.gif)
Gridding
To use the time advantage of the fast Fourier transform (FFT) algorithm, the visibilities must be interpolated onto a regular grid of size 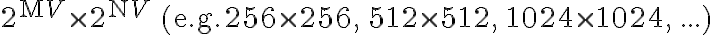 , resulting in an image of size
, resulting in an image of size 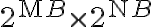 . This interpolation, also called gridding, is done at first by convolving the weighted discrete visibility
. This interpolation, also called gridding, is done at first by convolving the weighted discrete visibility 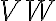 with an appropriate function
with an appropriate function 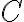 to obtain a continuous visibility distribution. This continuous visibility distribution is then resampled at points of the regular grid with spacings
to obtain a continuous visibility distribution. This continuous visibility distribution is then resampled at points of the regular grid with spacings 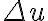 and
and 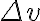 by multiplying a two-dimensional Shah-function
by multiplying a two-dimensional Shah-function 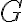 , given by
, given by
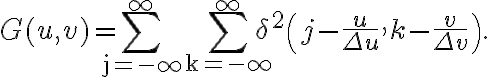
After these modifications, the visibility 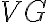 is given by
is given by ![\displaystyle V^\text{G} = G \cdot (C \star \star V^\text{W}) = G \cdot [C \star \star (W \cdot V^\text{S})] = G \cdot [C \star \star (W \cdot V \cdot S)] \displaystyle V^\text{G} = G \cdot (C \star \star V^\text{W}) = G \cdot [C \star \star (W \cdot V^\text{S})] = G \cdot [C \star \star (W \cdot V \cdot S)]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/24e98dae931507ec8c75522931b13c87.gif)
and the dirty image 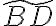 reads
reads![\displaystyle \tilde{B^\text{D}} = \mathcal{FT}[G] \star \star (\mathcal{FT}[C] \cdot \mathcal{FT}[V^\text{W}]) = \mathcal{FT}[G] \star \star \{ \mathcal{FT}[C] \cdot [\mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S])]\} \text{.} \displaystyle \tilde{B^\text{D}} = \mathcal{FT}[G] \star \star (\mathcal{FT}[C] \cdot \mathcal{FT}[V^\text{W}]) = \mathcal{FT}[G] \star \star \{ \mathcal{FT}[C] \cdot [\mathcal{FT}[W] \star \star (\mathcal{FT}[V] \star \star \mathcal{FT}[S])]\} \text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/1b44c8e537f9f7143cf62d73d416bec3.gif)
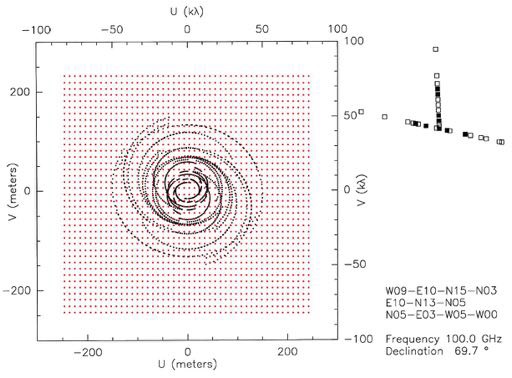
This gridding process is illustrated in the Fig. 2.29, in which real 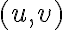 -tracks measured by the IRAM interferometer at Plateau de Bure in France are shown as black dotted ellipses. Furthermore, a regular grid, onto which the visibilities have been interpolated, is shown as red dots.
-tracks measured by the IRAM interferometer at Plateau de Bure in France are shown as black dotted ellipses. Furthermore, a regular grid, onto which the visibilities have been interpolated, is shown as red dots.
Since the sampling intervals 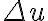 and
and 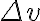 in the
in the 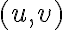 -plane are inversely proportional to the sampling intervals
-plane are inversely proportional to the sampling intervals 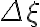 and
and 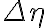 in the image plane (
in the image plane ( 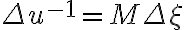 and
and 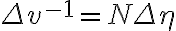 for a grid of size
for a grid of size 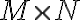 ), the maximum map size in one domain is given by the minimum sampling interval in the other. Therefore, it is important to choose appropriate sampling intervals
), the maximum map size in one domain is given by the minimum sampling interval in the other. Therefore, it is important to choose appropriate sampling intervals 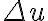 and
and 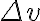 . If
. If 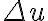 and
and 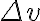 are chosen to be too large for example, this will result in artefacts in the image plane produced by reflections of structures from the map edges, which is called aliasing.
are chosen to be too large for example, this will result in artefacts in the image plane produced by reflections of structures from the map edges, which is called aliasing.
The most effective way to deal with this aliasing is to use a convolution function 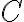 for which the Fourier transform in the image plane
for which the Fourier transform in the image plane ![\mathcal{FT}[C] \mathcal{FT}[C]](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/7265b9d7b7857f89d7fdad5bc301eb5a.gif) decreases rapidly at the image edges and is nearly constant over the image. Therefore, the simplest choice for the convolution function
decreases rapidly at the image edges and is nearly constant over the image. Therefore, the simplest choice for the convolution function 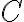 is a rectangular function, but with this choice the aliasing would be strongest. A better choice would be a sinc function, however a Gaussian-sinc function (product of a Gaussian and a sinc function) leads to the best suppression of aliasing.
is a rectangular function, but with this choice the aliasing would be strongest. A better choice would be a sinc function, however a Gaussian-sinc function (product of a Gaussian and a sinc function) leads to the best suppression of aliasing.
Finally, the gridding modifications must be corrected after the Fourier transform by dividing the dirty image 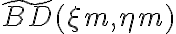 by the inverse Fourier transform of the gridding convolution function
by the inverse Fourier transform of the gridding convolution function 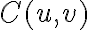 . Therefore, the so-called grid-corrected image
. Therefore, the so-called grid-corrected image 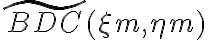 is given by
is given by} \text{.} \displaystyle \tilde{B^\text{D}_\text{C}}(\xi_\text{m},\eta_\text{m}) = \frac{\tilde{B^\text{D}}(\xi_\text{m},\eta_\text{m})}{\mathcal{FT}[C](u,v)} \text{.}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/38a39a2ff58598a9e9090adcf122a3df.gif)

![\displaystyle B^\text{D} = \mathcal{FT}[V^\text{S}] = \mathcal{FT}[V \cdot S] = \mathcal{FT}[V] \star \star \mathcal{FT}[S] \text{,} \displaystyle B^\text{D} = \mathcal{FT}[V^\text{S}] = \mathcal{FT}[V \cdot S] = \mathcal{FT}[V] \star \star \mathcal{FT}[S] \text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/ae19d1b8e17a3ebbdd115e1eeff5e233.gif)