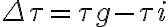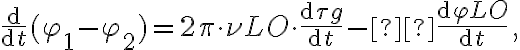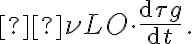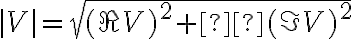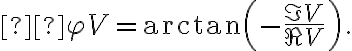Lecture - Fundamental Concepts
Tamamlama Gereklilikleri
4. Receiver Response
4.1. Heterodyne frequency conversion
The detectors of radio telescopes are diodes with quadratic current-voltage characteristics that require an input power of 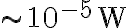 to work in the quadratic regime. The power
to work in the quadratic regime. The power 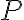 of the weak radio-astronomical signals entering the receiver is given by
of the weak radio-astronomical signals entering the receiver is given by
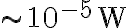 to work in the quadratic regime. The power
to work in the quadratic regime. The power 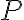 of the weak radio-astronomical signals entering the receiver is given by
of the weak radio-astronomical signals entering the receiver is given byin which 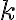 is the Boltzmann constant and
is the Boltzmann constant and 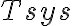 is the system temperature containing the receiver noise temperature and the antenna temperature. The antenna temperature is composed of the desired astronomical signal, a contribution from the earth's atmosphere, and possibly radiation from the ground. Due to that always present background the best case for the systemtemperature is
is the system temperature containing the receiver noise temperature and the antenna temperature. The antenna temperature is composed of the desired astronomical signal, a contribution from the earth's atmosphere, and possibly radiation from the ground. Due to that always present background the best case for the systemtemperature is 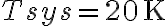 . Therefore, using a typical bandwidth of
. Therefore, using a typical bandwidth of 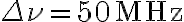 , the input power
, the input power 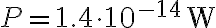 , meaning that the signal must be amplified by a factor of
, meaning that the signal must be amplified by a factor of 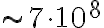 . However, amplification with such high factors is problematic, since the amplifying system becomes unstable due to feedback. A small amount of the power passing through the individual electronic components leaks out and reaches previous receiver elements, where it is again amplified. To circumvent this problem, the frequency of the signal
. However, amplification with such high factors is problematic, since the amplifying system becomes unstable due to feedback. A small amount of the power passing through the individual electronic components leaks out and reaches previous receiver elements, where it is again amplified. To circumvent this problem, the frequency of the signal 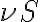 is down-converted to the lower intermediate frequency (IF) by mixing the signal with that of a local oscillator (LO), which decouples the signal path after the first amplification. This process is called heterodyne amplification or heterodyne frequency conversion.
is down-converted to the lower intermediate frequency (IF) by mixing the signal with that of a local oscillator (LO), which decouples the signal path after the first amplification. This process is called heterodyne amplification or heterodyne frequency conversion.
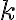 is the Boltzmann constant and
is the Boltzmann constant and 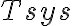 is the system temperature containing the receiver noise temperature and the antenna temperature. The antenna temperature is composed of the desired astronomical signal, a contribution from the earth's atmosphere, and possibly radiation from the ground. Due to that always present background the best case for the systemtemperature is
is the system temperature containing the receiver noise temperature and the antenna temperature. The antenna temperature is composed of the desired astronomical signal, a contribution from the earth's atmosphere, and possibly radiation from the ground. Due to that always present background the best case for the systemtemperature is 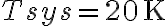 . Therefore, using a typical bandwidth of
. Therefore, using a typical bandwidth of 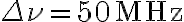 , the input power
, the input power 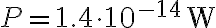 , meaning that the signal must be amplified by a factor of
, meaning that the signal must be amplified by a factor of 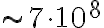 . However, amplification with such high factors is problematic, since the amplifying system becomes unstable due to feedback. A small amount of the power passing through the individual electronic components leaks out and reaches previous receiver elements, where it is again amplified. To circumvent this problem, the frequency of the signal
. However, amplification with such high factors is problematic, since the amplifying system becomes unstable due to feedback. A small amount of the power passing through the individual electronic components leaks out and reaches previous receiver elements, where it is again amplified. To circumvent this problem, the frequency of the signal 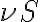 is down-converted to the lower intermediate frequency (IF) by mixing the signal with that of a local oscillator (LO), which decouples the signal path after the first amplification. This process is called heterodyne amplification or heterodyne frequency conversion.
is down-converted to the lower intermediate frequency (IF) by mixing the signal with that of a local oscillator (LO), which decouples the signal path after the first amplification. This process is called heterodyne amplification or heterodyne frequency conversion.Frequency down-conversion
The LO produces a signal at a well-defined and tunable frequency 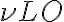 , close to the observing frequency
, close to the observing frequency 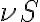 . To mix these two input signals, a semi-conductor diode with a non-linear current-voltage characteristic is used. The current-voltage relation of this diode can be written in terms of a Taylor expansion as
. To mix these two input signals, a semi-conductor diode with a non-linear current-voltage characteristic is used. The current-voltage relation of this diode can be written in terms of a Taylor expansion as
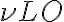 , close to the observing frequency
, close to the observing frequency 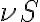 . To mix these two input signals, a semi-conductor diode with a non-linear current-voltage characteristic is used. The current-voltage relation of this diode can be written in terms of a Taylor expansion as
. To mix these two input signals, a semi-conductor diode with a non-linear current-voltage characteristic is used. The current-voltage relation of this diode can be written in terms of a Taylor expansion aswith
leading to a frequency spectrum containing frequencies of
Since the LO power 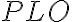 of higher harmonics decreases as
of higher harmonics decreases as 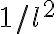 and usually the signal power
and usually the signal power 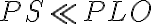 , only three terms of this frequency spectrum are important, namely:
, only three terms of this frequency spectrum are important, namely:
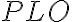 of higher harmonics decreases as
of higher harmonics decreases as 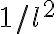 and usually the signal power
and usually the signal power 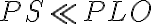 , only three terms of this frequency spectrum are important, namely:
, only three terms of this frequency spectrum are important, namely:the frequency sum
the intermediate frequency (IF)
and the image frequency
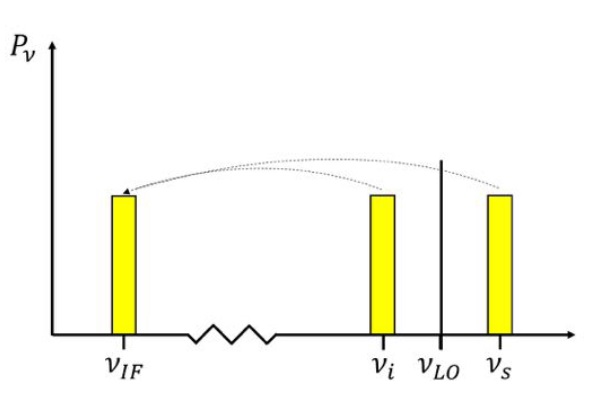
which is the "image" of 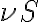 . Combining these terms, one obtains two high frequency (HF) bands that have equidistant separations from
. Combining these terms, one obtains two high frequency (HF) bands that have equidistant separations from 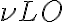 which correspond to the IF. For
which correspond to the IF. For 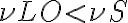 , these two HF bands correspond to the observing frequency, or signal frequency,
, these two HF bands correspond to the observing frequency, or signal frequency, 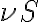 , and the image frequency
, and the image frequency 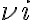 , and are denoted by
, and are denoted by
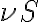 . Combining these terms, one obtains two high frequency (HF) bands that have equidistant separations from
. Combining these terms, one obtains two high frequency (HF) bands that have equidistant separations from 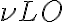 which correspond to the IF. For
which correspond to the IF. For 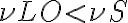 , these two HF bands correspond to the observing frequency, or signal frequency,
, these two HF bands correspond to the observing frequency, or signal frequency, 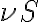 , and the image frequency
, and the image frequency 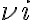 , and are denoted by
, and are denoted byFigure 2.26 illustrates the down-conversion of the two HF bands to the single IF band. The two HF bands 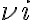 and
and 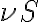 are called lower sideband (LSB) and upper sideband (USB), respectively. If both sidebands are used, the receiver operates in the so-called double-sideband mode. Otherwise, the receiver is said to operate in the single-sideband mode. To make sure that only the two HF bands are produced by the mixing process, an IF filter is used after the mixer to suppress all unwanted products of the mixing process (e.g.
are called lower sideband (LSB) and upper sideband (USB), respectively. If both sidebands are used, the receiver operates in the so-called double-sideband mode. Otherwise, the receiver is said to operate in the single-sideband mode. To make sure that only the two HF bands are produced by the mixing process, an IF filter is used after the mixer to suppress all unwanted products of the mixing process (e.g. 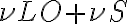 ).
).
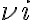 and
and 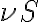 are called lower sideband (LSB) and upper sideband (USB), respectively. If both sidebands are used, the receiver operates in the so-called double-sideband mode. Otherwise, the receiver is said to operate in the single-sideband mode. To make sure that only the two HF bands are produced by the mixing process, an IF filter is used after the mixer to suppress all unwanted products of the mixing process (e.g.
are called lower sideband (LSB) and upper sideband (USB), respectively. If both sidebands are used, the receiver operates in the so-called double-sideband mode. Otherwise, the receiver is said to operate in the single-sideband mode. To make sure that only the two HF bands are produced by the mixing process, an IF filter is used after the mixer to suppress all unwanted products of the mixing process (e.g. 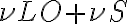 ).
).Advantages
Once the HF bands are down-converted to the lower IF band, further amplification can be performed. Because of the lower frequency, all electronic components after the mixer become more stable and easier to handle. Furthermore, after the heterodyne frequency conversion it is also possible to vary the observing frequency 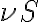 without changing any components following the mixer, which is essential for spectral-line measurements.
without changing any components following the mixer, which is essential for spectral-line measurements.
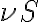 without changing any components following the mixer, which is essential for spectral-line measurements.
without changing any components following the mixer, which is essential for spectral-line measurements.The heterodyne frequency conversion also results in some important advantages in radio interferometry. As already seen before, the correlated power of a two-element interferometer is given by
in which 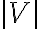 and
and 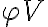 are the amplitude and phase of the complex visibility function,
are the amplitude and phase of the complex visibility function, 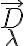 is the baseline between the two antennas in units of the observing wavelength and
is the baseline between the two antennas in units of the observing wavelength and 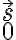 denotes the position of the observed radio source.
denotes the position of the observed radio source.
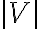 and
and 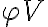 are the amplitude and phase of the complex visibility function,
are the amplitude and phase of the complex visibility function, 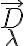 is the baseline between the two antennas in units of the observing wavelength and
is the baseline between the two antennas in units of the observing wavelength and 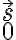 denotes the position of the observed radio source.
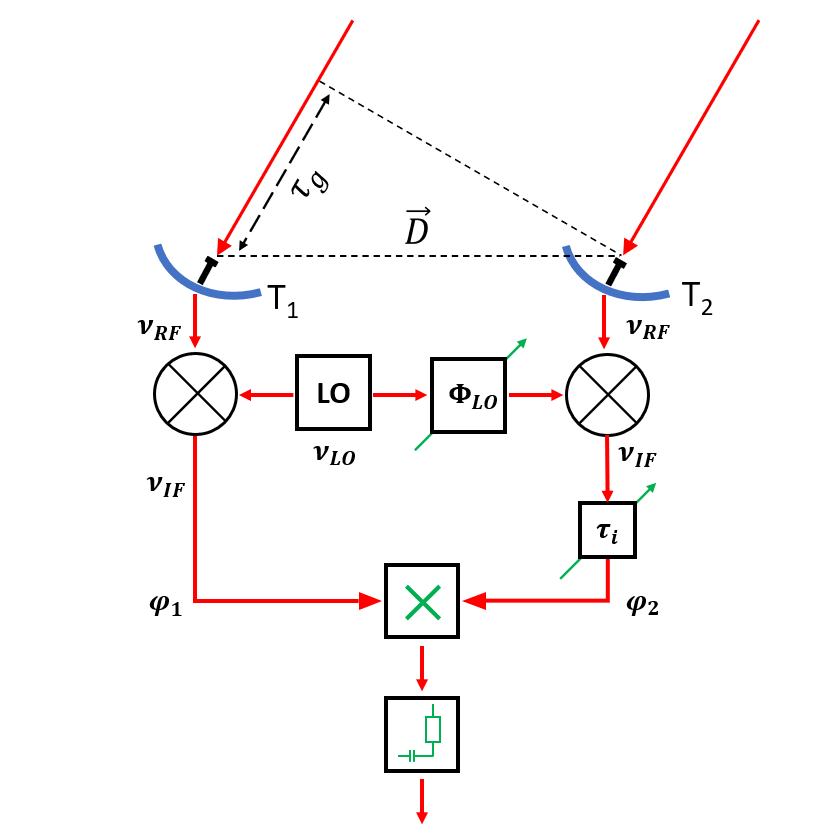
denotes the position of the observed radio source.Figure 2.27 illustrates such an interferometer with some modifications concerning the heterodyne frequency conversion. First, an artificial time lag 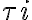 is introduced in one of the two branches of the receiver systems before the correlator. Second, a common LO signal is introduced into both mixers, with a phase shifter fed into one of the branches. Therefore, the resulting signal frequency
is introduced in one of the two branches of the receiver systems before the correlator. Second, a common LO signal is introduced into both mixers, with a phase shifter fed into one of the branches. Therefore, the resulting signal frequency 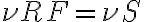 is given by
is given by
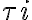 is introduced in one of the two branches of the receiver systems before the correlator. Second, a common LO signal is introduced into both mixers, with a phase shifter fed into one of the branches. Therefore, the resulting signal frequency
is introduced in one of the two branches of the receiver systems before the correlator. Second, a common LO signal is introduced into both mixers, with a phase shifter fed into one of the branches. Therefore, the resulting signal frequency 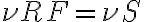 is given by
is given byin which 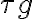 is the geometric time delay and
is the geometric time delay and 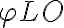 is the phase difference between the LO signals at the input of the mixers. The correlated power of such an interferometer can then be determined by changing the phase
is the phase difference between the LO signals at the input of the mixers. The correlated power of such an interferometer can then be determined by changing the phase 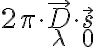 by
by  , leading to
, leading to
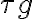 is the geometric time delay and
is the geometric time delay and 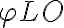 is the phase difference between the LO signals at the input of the mixers. The correlated power of such an interferometer can then be determined by changing the phase
is the phase difference between the LO signals at the input of the mixers. The correlated power of such an interferometer can then be determined by changing the phase 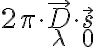 by
by  , leading to
, leading toTherefore, using heterodyne frequency conversion in radio interferometry leads to the possibility that the geometric delay 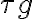 can be compensated by introducing an intrinsic time lag
can be compensated by introducing an intrinsic time lag 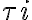 and that any phase variations due to the varying
and that any phase variations due to the varying 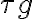 can be compensated by controlling
can be compensated by controlling 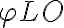 .
.
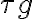 can be compensated by introducing an intrinsic time lag
can be compensated by introducing an intrinsic time lag 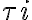 and that any phase variations due to the varying
and that any phase variations due to the varying 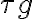 can be compensated by controlling
can be compensated by controlling 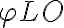 .
. Fringe rotation and complex correlators
By varying 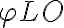 , the fringe frequency at which the interference pattern changes for each telescope pair due to the varying hour angle can be reduced. This is called fringe rotation. Looking at the time derivative of
, the fringe frequency at which the interference pattern changes for each telescope pair due to the varying hour angle can be reduced. This is called fringe rotation. Looking at the time derivative of  , given by
, given by
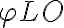 , the fringe frequency at which the interference pattern changes for each telescope pair due to the varying hour angle can be reduced. This is called fringe rotation. Looking at the time derivative of
, the fringe frequency at which the interference pattern changes for each telescope pair due to the varying hour angle can be reduced. This is called fringe rotation. Looking at the time derivative of  , given by
, given byone can see that it is even possible to stop the fringes by varying 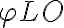 at a speed that is identical to the so-called natural fringe frequency, given by the term
at a speed that is identical to the so-called natural fringe frequency, given by the term
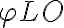 at a speed that is identical to the so-called natural fringe frequency, given by the term
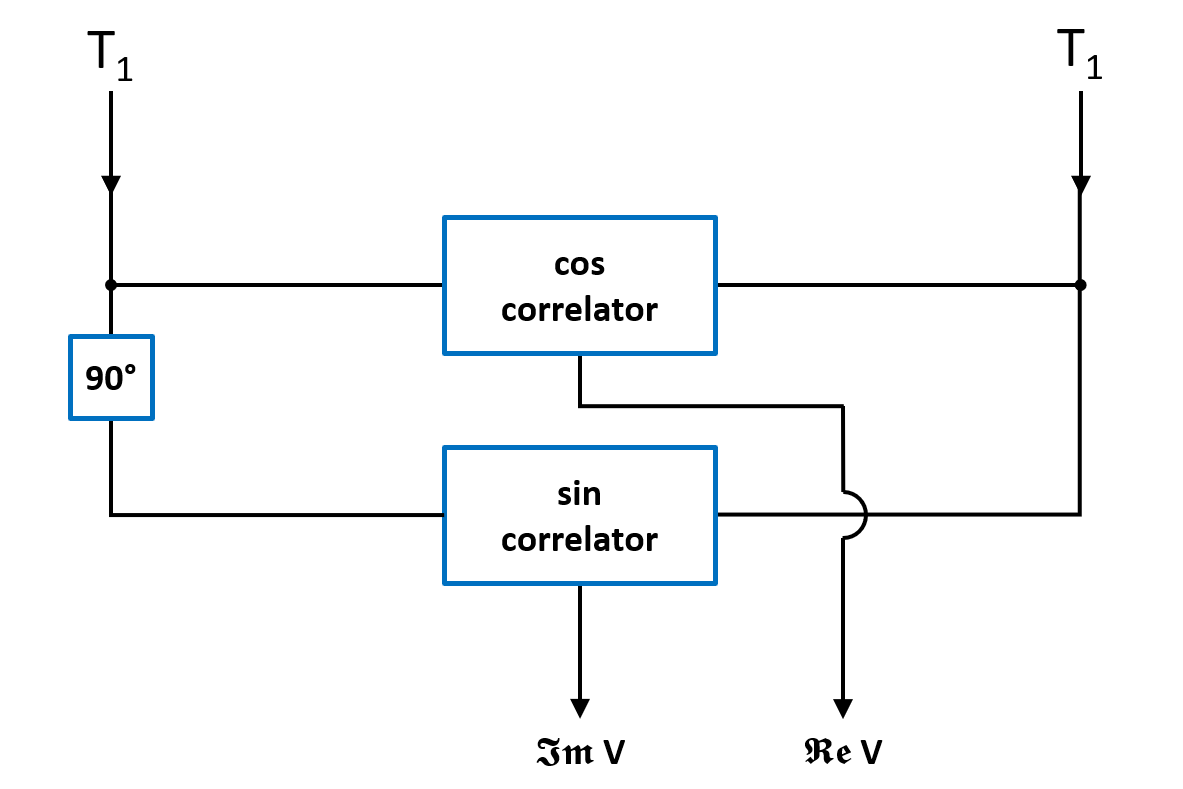
at a speed that is identical to the so-called natural fringe frequency, given by the termThis is then called fringe stopping. After rotating or stopping the fringes, it is also much easier to measure the amplitude and phase of the complex visibility by using a so-called complex correlator (see Fig. 2.28). Here, two correlations are performed: one with the two original signals, leading to a co-sinusoidal output signal that represents the real part of the visibility 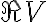 , and one that has a
, and one that has a 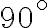 -phase shift in one of its branches prior to the correlation, leading to a sinusoidal output signal that corresponds to the imaginary part of the visibility
-phase shift in one of its branches prior to the correlation, leading to a sinusoidal output signal that corresponds to the imaginary part of the visibility 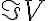 . With these output signals, the amplitude
. With these output signals, the amplitude 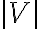 and phase
and phase 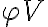 of the visibility can be calculated by
of the visibility can be calculated by
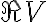 , and one that has a
, and one that has a 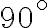 -phase shift in one of its branches prior to the correlation, leading to a sinusoidal output signal that corresponds to the imaginary part of the visibility
-phase shift in one of its branches prior to the correlation, leading to a sinusoidal output signal that corresponds to the imaginary part of the visibility 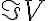 . With these output signals, the amplitude
. With these output signals, the amplitude 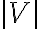 and phase
and phase 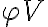 of the visibility can be calculated by
of the visibility can be calculated byand

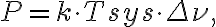
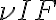
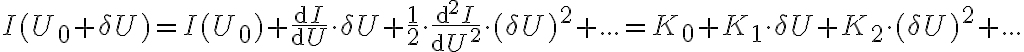
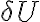
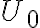
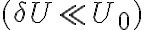
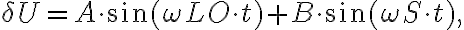
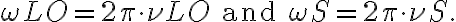
![\displaystyle \begin{array}{rl} I = & K_0 + K_1 \cdot \left[A \cdot \sin (\omega_\text{LO} \cdot t) + B \cdot \sin (\omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot \left[\frac{A^2}{2} + \frac{B^2}{2}\right] \\ & - K_2 \cdot \left[\frac{A^2}{2} \cdot \cos (2 \cdot \omega_\text{LO} \cdot t) + \frac{B^2}{2} \cdot \cos (2 \cdot \omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} - \omega_\text{S}) \cdot t\right] \\ & - K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} + \omega_\text{S}) \cdot t\right] \text{,} \end{array} \displaystyle \begin{array}{rl} I = & K_0 + K_1 \cdot \left[A \cdot \sin (\omega_\text{LO} \cdot t) + B \cdot \sin (\omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot \left[\frac{A^2}{2} + \frac{B^2}{2}\right] \\ & - K_2 \cdot \left[\frac{A^2}{2} \cdot \cos (2 \cdot \omega_\text{LO} \cdot t) + \frac{B^2}{2} \cdot \cos (2 \cdot \omega_\text{S} \cdot t)\right] \\ & + K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} - \omega_\text{S}) \cdot t\right] \\ & - K_2 \cdot A \cdot B \cdot \cos \left[(\omega_\text{LO} + \omega_\text{S}) \cdot t\right] \text{,} \end{array}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/592ca3c1f2371daedb504e40c89cc654.gif)
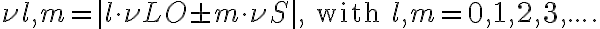
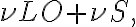
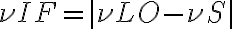
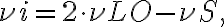
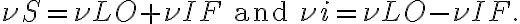
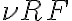
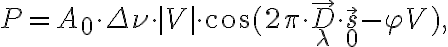
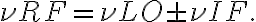
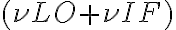
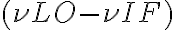
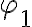
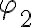
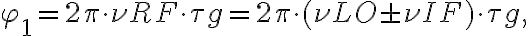
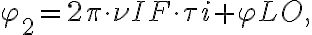
![\displaystyle P = A_0 \cdot \Delta \nu \cdot |V| \cdot \cos [2 \pi (\nu_\text{LO} \cdot \tau_\text{g} \pm \nu_\text{IF} \cdot \Delta \tau) - \varphi_\text{V} - \varphi_\text{LO}] \text{,} \displaystyle P = A_0 \cdot \Delta \nu \cdot |V| \cdot \cos [2 \pi (\nu_\text{LO} \cdot \tau_\text{g} \pm \nu_\text{IF} \cdot \Delta \tau) - \varphi_\text{V} - \varphi_\text{LO}] \text{,}](https://wuecampus.uni-wuerzburg.de/moodle/filter/tex/pix.php/b0bdf3019af0affc0b3b21ed44cbc7bc.gif)