Demokurs: Introduction to Engineering Mathematics: Exercises

1. Functions

1.7. Exercises

Tasks for Chapter 1 "Functions"

Task 1: Parabolas I

The graphs of the functions $f$ , $g$ with $f(x) = ax^2+ bx + c$ and $g(x) = d(x-e)^2+ h$ should show the samme parabola. What is the relationship between the variables $a$ , $b$ , $c$ , $d$ , $e$ and $h$ ?

Task 2: Parabolas II

We consider the parables \(\P_b) with the equation $f(x) = 2x^2+ bx + 1$ , $b \in \mathbb{R}$ .

Determine the vertex $S_b$ of the parabolas $P_b$ (thus depending on $b$ ).
Draw - for example with the help of the program GeoGebra (downloadable free of charge from http://www.geogebra.at) the locus line $OS_b$ on which the vertex of $P_b$ moves when $b$ is varied. A screenshot of this task should be included in the solution of the task.
Determine the equation for the locus line $OS$ .

Task 3: Exponential function

Compare the two functions with $y = a \cdot 2^x$ and $y = 2^{(x+d)}$ for different values $a,d \in \mathbb{R}$ . For which $a$ or $d$ -values do the graphs of the two functions match?
The general exponential function can be calculated with the equation $f(x) = a \cdot b^{cx+d}$ with $a,c,d \in \mathbb{R}; b \in \mathbb{R}^+$ . This equation is equivalent to an equation with only three parameters $A,B,C$ where $A,B,C \in \mathbb{R}$ or $\mathbb{R}^+$ . Give the relationship between $A,B, C$ and $a,b,c,d$ .

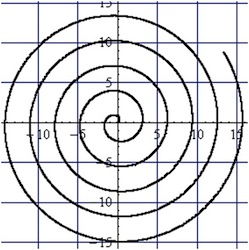
Task 4: Spiral

Draw the curve $K(t) = (t \cdot \cos(t), t \cdot \sin(t))$ for $0 < t < 20$ . The curve can be thought of as resulting from a movement and dynamically interpreted, if $t$ is understood as time. This curve is called a spiral.

Describe this movement!
Specify the equation of the shown spiral!

Task 5: Ellipse

Given is an ellipse $E(x,y): \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ ; $a,b \in \mathbb{R}^+$ . Specify the equation of the tangent to the ellipse in the ellipse point $P(x_0,y_0)$ .

Note: Start from the circle $K_a: x^2+ y^2= a^2$ and create $E$ by stretching or compressing $K_a$ by the factor $\frac{b}{a}$ parallel to the $y$ -axis. Then start from a circle tangent.

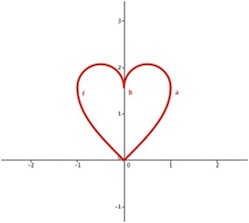
Task 6: The heart

There are different possibilities how to draw a heart using mathematical functions. In particular a heart can have many different forms. Using function pieces (in GeoGebra) draw a heart shape. The image on the right shows one example of how it can be achieved.

Task 7: Function of two variables

Describe the graph $G$ of the function $f(x,y) = x^2+ y^2$ by cutting $G$ with selected planes and describing the resulting figures.
Consider the two planes $f(x,y) = 4x + y + 3$ and $g(x,y) = -x + 3y - 5$ in a joint coordinate system. Show that these two planes are perpendicular to each other.