Demokurs: Introduction to Engineering Mathematics
1. Functions
1.2. Power Functions, Polynomials and Power Series

In this chapter we revise the characteristics of power functions and polynomials. Then, in an optional section, we introduce another analysis concept -- the power series.

Power functions
Definition 1: Power function with positive integer exponent
A power function with a positive integer exponent is a function of the form: \[f : x\mapsto a\cdot x^n \qquad a\in\mathbb{R},\ n\in\mathbb{N},\ D=\mathbb{R}\]
Setting \(n=0\) provides a constant function \(f(x)=a.\)
Note: We have already met two specific examples of power functions in the last chapter: For \(n=1\) we have the pure linear function \(f\) where \(f(x) = ax\) and for \(n=2\) we have the pure quadratic function \(f\) where \(f(x) = ax^2\). Additionally, for \(n=0\) we get the special case of a constant function \(f(x) = a∙x^0 = a∙1 = a\).
Exercise.
Vary the parameter \(a\) on the adjacent example for \(f(x) = a\cdot x^3\). Comment on how the graph changes.

Definition 2: Power function with integer exponents
A power function with an integer exponent is a function of the form: \[f : x\mapsto a\cdot x^z \qquad a\in\mathbb{R},\ z\in\mathbb{Z},\ D=\mathbb{R}\backslash\{0\}\]
They can be separated into two groups, which have opposite characteristics:
-
\(f(x) = a\cdot x^n\) (positive integer exponent, \(n>0\)): These functions have one root at \(x=0\) and grow without bounds for large \(|x|\) (tend towards plus or minus infinity). They are continuous on the whole of \(\mathbb{R}\). Their graphs always have one branch and are called parabolas of order \(n\).
-
\(f(x) = a\cdot x^{-n}\) (negative integer exponent, \(-n<0\)): These functions have a pole at \(x=0\) and approach 0 for large \(|x|\). There are continuous on \(\mathbb{R}\backslash\{0\}\). We call their graphs hyperbole of order \(n\). Because of the pole, they have two branches.
The graphs of power functions with odd exponents are point-symmetric about the origin, while those of power functions with even exponents are axially-symmetric about the \(y\)-axis.
\[f(-x) = (-x)^2 = x^2 = f(x)\]
\[f(-x) = (-x)^3 = -(x^3) = -f(x)\]
Parabolas of order \(n\) - the building blocks of polynomials
For growing \(x\) the absolute value of \(x^n\) increases continuously and diverges towards \(\infty\).
For growing \(x\) the denominator (actually its absolute value) increases and the fraction converges towards \(0\).

Definition 3: Power functions with fractions in the exponents
A power function with a fraction in the exponent is a function of the form: \[f : x\mapsto a\cdot x^{\frac{1}{n}} \qquad a\in\mathbb{R},\ n\in\mathbb{N},\ D=\mathbb{R}^+_0\]
Exercise.
On the right are the graphs of the function \(f\) where \(f(x)=x^{\frac{1}{n}}\) for \(n \in \{2,3,4,5,6\}\). Describe these graphs, paying particular attention to the domain, monotonicity, and the largest and smallest values of the function. Are there points common to all graphs of these functions? Justify this!
Example 1: Root function
A particular example of a power function is the function \[f : \mathbb{R}^+_0\rightarrow\mathbb{R}^+_0, x\mapsto\sqrt{x}=x^{\frac{1}{2}}\] which takes the square root of every positive number. Analogously the \(k\)-th roots \(\sqrt[k]{x}\) are also power functions thanks to the identity \(\sqrt[k]{x}=x^{\frac{1}{k}}.\) The \(k\)-th root function \(f\) where \(f(x)=x^{\frac{1}{k}}\) is the inverse of the power function \(g\) where \(g(x) = x^k\). Also \(g\) is the inverse of \(f\).

Definition 4: Power functions with negative fractions in the exponent
A power function with a negative fraction in the exponent is a function of the form: \[f : x\mapsto a\cdot x^{-\frac{1}{n}} \qquad a\in\mathbb{R},\ n\in\mathbb{N},\ D=\mathbb{R}^+\]
Exercise.
Compare the graphs of the functions with negative fractions in the exponents (blue) with the graphs of the functions that were introduced earlier with positive fractions in the exponents (red dotted). Pay particular attention to the domain, symmetry, monotonicity and the largest and smallest values of the function. Are there points which all graphs have in common? Justify this.

Definition 5: Power functions with rational number exponents
A power function with a rational number exponent is a function of the form: \[f : x\mapsto a\cdot x^{\frac{p}{q}} \qquad a\in\mathbb{R},\ p\in\mathbb{Z},\ q\in\mathbb{N},\ D=\mathbb{R}^+\]
Exercise.
Compare the graphs of power function with rational exponents (blue) with those we met in the above sections (red and purple dotted); by using the scroll bar you can alter the exponents. Describe the similarities and differences of the graphs, paying particular attention to the domain and symmetry.
Power functions with rational number exponents
The representation of functions of the form \(f(x) = (\sqrt[k]{x})^p\) as \(f(x) = x^{\frac{p}{k}}\) plays a role when differentiating functions as the common rules for derivatives are transferred to root-functions.
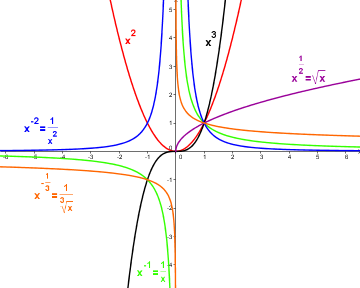
Various power functions.

Polynomials
Polynomials are constructed by adding up power functions \(a \cdot x^n\) where \(n\) is a natural number. They are defined and continuous over the whole of \(\mathbb{R}\).
Definition 6: Polynomial of degree \(n\)
For \(a_0, a_1,\ldots, a_n \in\mathbb{R},\) \[p : \mathbb{R}\rightarrow\mathbb{R}, x\mapsto\sum^n_{k=0}a_kx^k = a_0+a_1^x+a_2x^2+\ldots+a_nx^n\] is called a polynomial of degree \(n\), when \(a_n\neq 0.\)
So, per definition constant, linear, quadratic and power functions are polynomials.
The behaviour of the graphs of polynomials with degree \(>2\) is not as easy to determine as for graphs in special cases like constant, linear and quadratic functions. To determine the characteristics of these polynomials and their graphs, we use the method of curve sketching taught in school (see below).
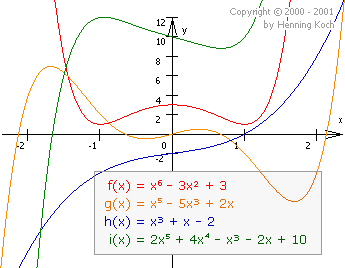
Various polynomial functions.

New terms:
-
Power function
-
Polynomials
-
Power series
Short revision exercises

Exercise 1.
Sketch the following power functions: \(x^3\), \(x^{\frac{1}{3}}\), \(x^{-3}\), \(x^{-\frac{1}{3}}\)

Exercise 2.
Specify the type and position of the extrema, inflection points and the roots for the polynomial function \[f(x)=-\frac{1}{4}x^4+\frac{3}{2}x^2-2x-2.\]


