

Was ist eigentlich Mathematisches Modellieren? Folgendes Beispiel aus dem Wissenschaftsjahr 2008 illustriert worum es geht:

Abbildung 1 - Quelle: Link

Dieses Beispiel zeigt, dass sich Mathematik verwenden lässt, um einen Ausschnitt aus der Realität zu beschreiben. Manchmal mag das auf den ersten Blick künstlich und erzwungen wirken, denn was hilft es dem Skateboarder, wenn er weiß, dass seine Flugkurve grob einer Parabel folgt? Viele professionelle Skateboarder streben danach, die bisherigen Grenzen des Sports zu erweitern. Wie in jedem anderen Sport auch gilt bei der Jagd nach Rekorden häufig: höher, schneller, weiter. Der Skateboarder Dany Way stellte sich im Jahr 2003 die Frage, ob er nicht über die chinesische Mauer springen und damit einen neuen Rekord aufstellen könnte. Eine Modellierung dieser Situation mit Schülerinnen und Schüler während einer Projektwoche 2016 zeigt, dass diese Frage durchaus auch für Nichtskateboarder*innen spannend und für den Mathematikunterricht reichhaltig ist.

Kann man mit einem Skateboard über die chinesische Mauer springen?
Zunächst gilt es, sich einige Fragen zur Mauer selbst und zu verschiedenen Sprungvarianten zu stellen und zu beantworten: Wie hoch und wie breit ist die Mauer? Die Mauer variiert in der Höhe zwischen 4 und 16 Metern (6 bis 9 Meter im Gebiet um Peking), während die Breite im Normalfall zwischen 4 und 8 Metern liegt. Das bedeutet, dass man sich für die Beantwortung der Frage entscheiden muss, welchen Wert man verwenden möchte.
Wie soll der Skateboarder über die Mauer springen? Ohne Zuhilfenahme einer Rampe wird es kein Mensch schaffen, mit einem normalen Skateboard vier Meter hoch zu springen. Eine Rampe kann allerdings ganz unterschiedlich gebaut sein: Der Absprungpunkt könnte möglichst nah am Boden oder sogar über der Mauerkrone liegen. Auch der Absprungwinkel lässt sich durch die Höhe und den Winkel der Absprungrampe beliebig festlegen. Je nachdem, welche Variante gewählt wird, ergeben sich unterschiedliche Antworten auf die Frage.
Für die folgende Modellierung legen wir fest: Der Absprungpunkt soll nicht oberhalb der Mauerkrone liegen. Für die Mauer nehmen wir eine Höhe von 13 Metern und eine Breite von 21 Metern an (Die hier genannten Werte orientieren sich am Sprung von Dany Way). Alle anderen Werte für die Rampe bestimmen wir anhand dieser Festlegung minimal. Die Form der Rampe orientiert sich wiederum am Original und sieht schematisch folgendermaßen aus:
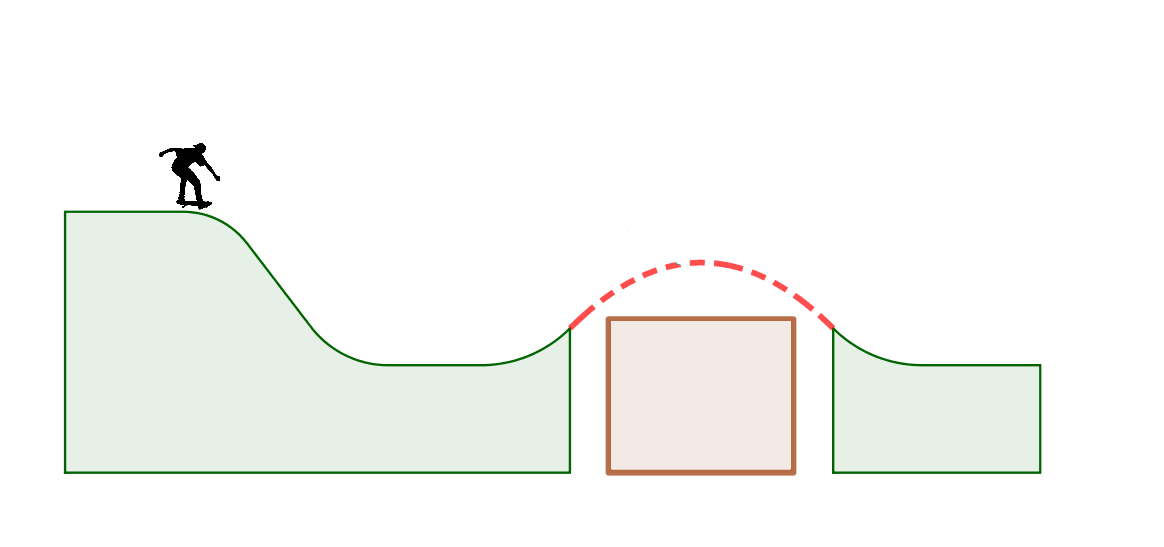
Eine Rampe lässt sich in der Seitenansicht mathematisch als Graph einer Funktion beschreiben. Für eine komplexe Rampe wird man zusammengesetzte Funktionen verwenden, um möglichst nah an die Realität heranzukommen. Wie man im Bild erkennen kann, ist der Anfang der Anfahrtsrampe ziemlich linear im Verlauf und geht erst nahe am Boden in eine gebogene Form über. Für den Bogen hat man auch verschiedene Möglichkeiten, so könnte man nach einer Parabel suchen oder einen Kreisbogen verwenden. Eine sinnvolle Bedingung ist, dass der Übergang zwischen den beiden Funktionsstücken glatt ist, d.h. dass der Skateboarder keinen allzu großen Ruck beim Übergang spürt.
Mathematisch lässt sich dies mithilfe der Ableitungen der beiden Funktionsterme untersuchen. Nur wenn die Ableitungen im Punkt des Zusammentreffens identisch sind, ist der Übergang glatt, d.h. es gibt keinen Knick.
Schülerinnen und Schüler müssen nach der entsprechenden Ableitung auch noch weitere Parameter des gesuchten Funktionsgraphen bestimmen, im Falle eines Kreisbogens z.B. den zugehörigen Mittelpunkt.
Anstatt Rechnungen selbst durchzuführen, kann man auch mit Hilfe eines Computerprogramms wie GeoGebra die Situation modellieren und experimentieren, welche Parameter für die verschiedenen Funktionsgraphen zu einer Lösung des Problems führen.
In eine solche Simulation gehen natürlich ebenfalls viele Überlegungen und Annahmen mit ein, etwa eine Festlegung für die maximale Höhe der Anfahrtsrampe sowie deren Winkel. Aber auch der Flug des Skateboarders muss als schräger Wurf modelliert werden. Dafür gilt:
Physikalisches
Potentielle Energie: \(E_{pot} = m \cdot g \cdot h \)
Kinetische Energie: \(E_{kin} = \frac{1}{2} \cdot m \cdot v^2 \)
Zeit-Ort-Gesetze: \(x(t) = v_0 \cos (\alpha) \cdot t,\quad y(t) = y_0 + v_0 \sin (\alpha) \cdot t - \frac{1}{2} \cdot g \cdot t^2 \) mit \(v_0\): Absprunggeschwindigkeit, \( \alpha \): Absprungwinkel
Unter Vernachlässigung der Reibung und des Luftwiderstands gilt, dass die Änderung der potentiellen Energie zwischen dem höchsten Punkt der Anfahrtsrampe und der Spitze der Absprungrampe in kinetische Energie umgewandelt wird.
Ziel ist es, dass der Skateboarder die Mauer mit Breite 22m überwinden können soll. Die Absprunghöhe legen wir auf die Höhe der Mauerkrone. Dann muss der Skateboarder in x-Richtung mindestens 22m weit fliegen, um nicht auf der Mauer zu landen. Mit diesen Überlegungen lässt sich z.B. in GeoGebra ein Modell erstellen, bei dem dynamisch die Höhe der Anfahrtsrampe, die Höhe des Absprungpunkts (beides zum Niveau des Flats der Anfahrtsrampe), die Masse des Skateboarders und der Absprungwinkel variieren lassen. Setzt man die obigen Formeln ebenfalls um, so kann man aus \( y(t) \) die Flugdauer bzw. den Zeitpunkt bestimmen, bis der Skateboarder wieder auf Höhe der Mauerkrone angekommen ist. Damit folgt dann aus \(x(t) \) die erreichte Flugweite in x-Richtung. Es fällt hier auf, dass es nicht nur eine, sondern mehrere Lösungen gibt. Eine davon lässt sich durch folgende Werte beschreiben: \[ \alpha = 45^\circ, \: h_0 = 12,9\text{m}, \: h_1 = 1,8\text{m} \] Die Flugdauer dabei beträgt 2,13s und die Flugweite (in x-Richtung) 22,2m. Mathematisch ist das innerhalb des Modells zwar zutreffend, aber unter dem Aspekt der Sicherheit möchte der Skateboarder vermutlich etwas weiter fliegen und nicht nur 20cm Puffer haben. Dies zeigt sich auch in einem Vergleich mit den Werten der echten Rampe: Der Höhenunterschied zwischen Start- und Absprungpunkt beträgt etwa 10 – 12 Meter (im Modell nur 11,1 Meter), die Höhe der Anfahrtsrampe wird mit knapp 17 Metern angegeben. Über die Höhe des Absprungpunkts sind keine Angaben zu finden, aber eine grobe Schätzung (vgl. Bild oben) lässt 4 – 6 Meter realistisch erscheinen.

Prüfen Sie das mathematische Modell und die Modellierung kritisch. Welche Annahmen würden Sie anders treffen?
Die hier vorgestellte Modellierung stellt nur einen Ausschnitt dar und deckt nicht das ganze Thema ab. Sie können selbst tätig werden und an dieser Modellierung weiterarbeiten. Einige Anregungen dazu:
- Wie soll die Rampe zur Landung am besten gebaut sein? Wovon hängt ihre Form ab?
- Welche Form ist an den Übergangen zwischen zwei linearen Rampenstücken am besten geeignet, um diese miteinander zu verbinden?
- Vielleicht gibt es in Ihrer Stadt auch einen Skatepark in Ihrer Nähe. Spazieren Sie doch einmal dort vorbei und schauen Sie, ob sich dort nicht noch weitere spannende Fragen für Schülerinnen und Schüler ergeben.






