Schulmathematik unter didaktischen Gesichtspunkten: Stochastik in der Sekundarstufe II (Demo-Kurs)
2. Zentrale Sätze der Stochastik
2.1. Die Tschebyscheff-Ungleichung und das schwache Gesetz der großen Zahlen


Ausgangspunkt: Erwartungswert und Varianz
Die Kennwerte Erwartungswert und Varianz einer Zufallsvariablen lassen Rückschlüsse auf deren zugrunde liegende Verteilung zu, auch wenn diese nicht bekannt ist.
Dabei stellt die Varianz ein Maß für die Streuung der Werte, die \(X\) annimmt, um den Erwartungswert \(E(X)\) dar. Sie ermöglicht es, Schranken für die Wahrscheinlichkeit zu berechnen, dass ein Wert der Zufallsvariable \(X\) von ihrem Erwartungswert \(E(X)\) abweicht (bzw., wie groß diese Abweichung ist).
So lässt sich bspw. zu einer positiven Zahl \(a\) fragen, mit welcher Wahrscheinlichkeit die Zufallsvariable \(X\) um weniger als \(a\) von ihrem Erwartungswert abweicht, dass also gilt \(E(X)-a < X < E(X)+a\), bzw. \(|X-E(X)| < a\)
Die Werte von \(X\) liegen also innerhalb des folgenden Intervalls \(A\):
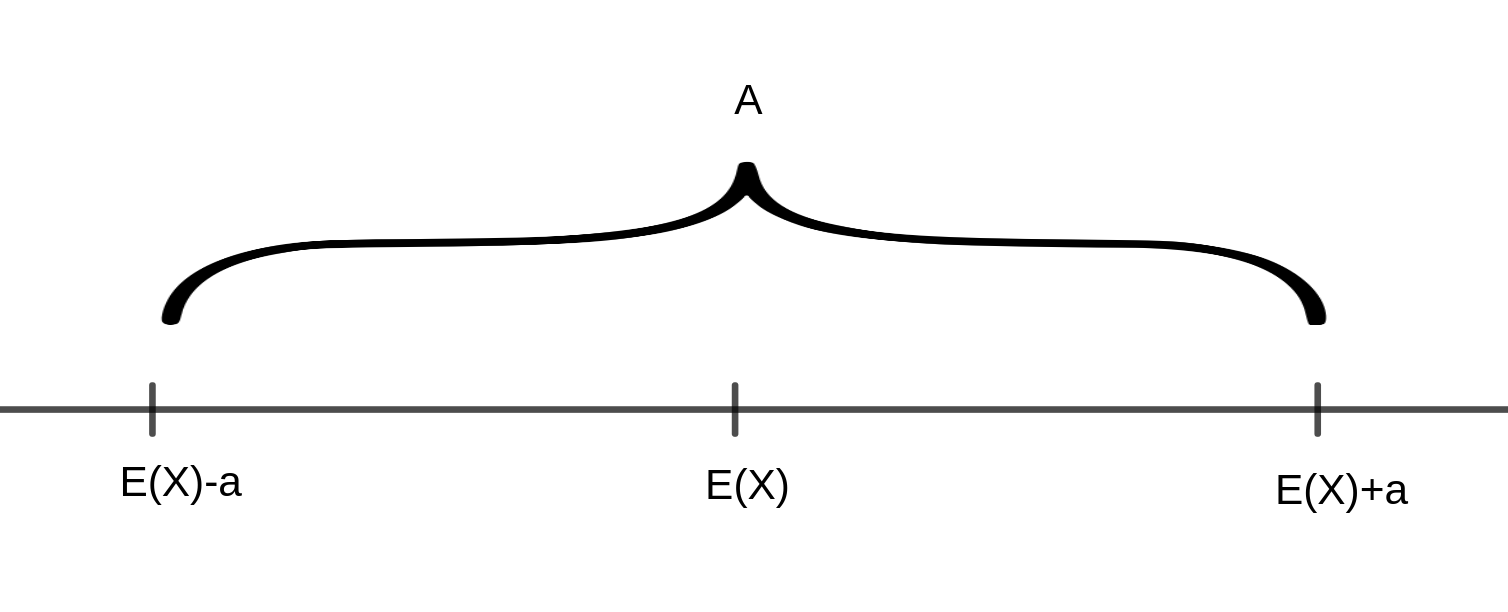
Die Gegenwahrscheinlichkeit gibt an, mit welcher Wahrscheinlichkeit die Werte von \(X\) außerhalb dieses Intervalls liegen, also \(|X-E(X)|\geq a\)
Letztere lässt sich mit Hilfe der Ungleichung von Tschebyscheff abschätzen:

Satz (Ungleichung von Tschebyscheff)
Sei \(X\) eine diskrete Zufallsvariable mit dem Erwartungswert \(E(X)=\mu\) und der Varianz \(V(X)=\sigma ^2\). Dann gilt für jede Zahl \(a>0\)
\[P(|X-E(X)|\geq a)\leq \frac{V(X)}{a^2}\]
Unter Verwendung des Gegenereignisses erhält man die folgende – gleichwertige – Formulierung:
\[P(|X-E(X)|< a )\geq 1-\frac{V(X)}{a^2}\]
Anmerkungen:
- Die Ungleichung von Tschebyscheff gilt nicht nur für diskrete, sondern auch für abstrakte Zufallsvariablen.
- Die Ungleichung ist nur dann nützlich, wenn \(\sigma =\sqrt{(V(X))} < a\) ist. Andernfalls erhält man lediglich die triviale Aussage, dass die Wahrscheinlichkeit \(\leq 1\) ist bzw. \(\leq t\) für eine Zahl \(t>1\).
- Die Ungleichung gilt für beliebige Zufallsvariablen und ist daher in ihrer Allgemeingültigkeit von theoretischem Nutzen. Für spezielle Verteilungen gibt es allerdings bessere Abschätzungen.
Aus der Ungleichung von Tschebyscheff lassen sich Folgerungen über die Lage der „Wahrscheinlichkeitsmasse“ ableiten:
Setzt man für a ein ganzzahliges Vielfaches \(k\cdot\sigma\) der Standardabweichung \(\sigma =\sqrt{V(X)}\) ein, so ergibt sich:
\[P(|X-E(X)|\geq k\sigma )\leq\frac{1}{k^2}\]
bzw.
\[P(|X-E(X)|< k\sigma )\geq 1-\frac{1}{k^2}\]
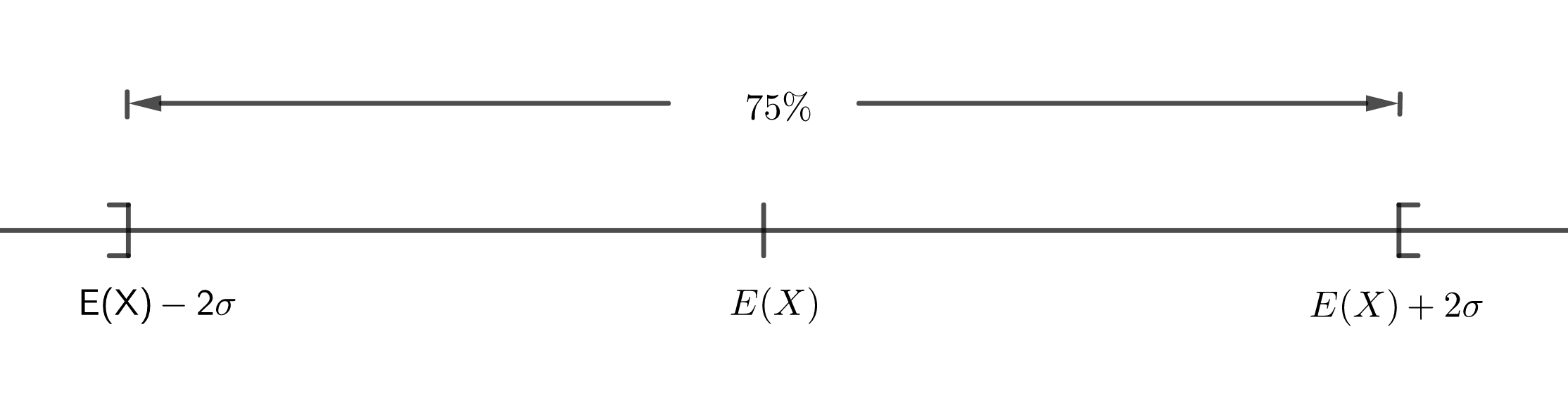
Für \(k=2\) ergibt sich bspw.
\[P(|X-E(X)|< 2\sigma )\geq \frac{3}{4}\]
Dies bedeutet, dass die Wahrscheinlichkeit, dass \(X\) Werte annimmt, die sich um weniger als zwei Standardabweichungen vom Erwartungswert \(E(X)\) unterscheiden, bei mehr als 75% liegt. D.h., dass mindestens 75% der vorhandenen „Wahrscheinlichkeitsmasse“ (von der Größe 1) auf das Intervall \(]E(X)-2\sigma ,E(X)+2\sigma [\) entfallen:

Beispiel - Ziehen mit Zurücklegen
Eine Urne enthalte 12 rote und 8 blaue Kugeln. Nacheinander werden 5 Kugeln mit Zurücklegen gezogen. Dabei soll die Zufallsvariable \(X\) die Anzahl der gezogenen roten Kugeln beschreiben.
- Wie groß ist der Erwartungswert \(E(X)\) der Zufallsvariablen?
Es wird eine Binomialverteilung zugrunde gelegt. \[E(X)=n\cdot p\text{ mit }n=5\text{ und }p=\frac{12}{20}=\frac{3}{5}\] Also ergibt sich \(E(X)=3\). - Berechnen Sie mit Hilfe der Tschebyscheff’schen Ungleichung \(P(|X-3|\geq 1)\).
Zunächst wird die Varianz \(V(X)\) berechnet: \[V(X)=n\cdot p\cdot (1-p)=5\cdot\frac{3}{5}\cdot\frac{2}{5}=\frac{6}{5}=1.2\] Mit der Ungleichung von Tschebyscheff folgt dann: \[P(|X-3|\geq 1)\leq \frac{1.2}{1^2}=1.2 \] Da für jede Wahrscheinlichkeit \(P\) gilt, dass \(P\leq 1\), ist diese Aussage trivial. Eine präzise Berechnung erfolgt unter 3). - Berechnen Sie P(|X-3|≥1) „exakt“ für die vorliegende Verteilung.
Es gilt: \[P(|X-3|\geq 1)=1-P(|X-3|< 1)\] \(X\) nimmt die Werte 0,1,2,3,4,5 an. \(|X-3|< 1\) gilt dabei nur für \(X=3\). \[P(X=3)={5\choose 3}\cdot {3\choose 5}^\cdot{2\choose 5}^2=10\cdot \frac{27}{125}\cdot \frac{4}{25}\approx 0.3456\] Damit gilt: \[P(|X-3|\geq 1)=1-0.3456=0.6544\approx 0.65\]

Schwaches Gesetz großer Zahlen
Das schwache Gesetz großer Zahlen (SGGZ) nach Jakob Bernoulli stellt die Verbindung her zwischen dem formalen Wahrscheinlichkeitsbegriff und
- der in der Realität zu beobachtenden Stabilität relativer Häufigkeiten
- der Verwendung der relativen Häufigkeit eines Ereignisses als Schätzwert für dessen Wahrscheinlichkeit.
Analog zu Kütting (1999) beschränkt sich dieser Kurs im Hinblick auf das SGGZ auf die Betrachtung von relativen Häufigkeiten in Bernoulli-Ketten der Länge \(n\).

Satz (Schwaches Gesetz großer Zahlen)
Es sei \(A\) ein Ereignis, das bei einem Zufallsexperiment mit der Wahrscheinlichkeit \(P(A)=p\) eintrete. Die relative Häufigkeit des Ereignisses \(A\) bei \(n\) unabhängigen Wiederholungen des Zufallsexperiments sei mit \(h_n\) (Bernoulli-Kette der Länge \(n\)) bezeichnet. Dann gilt für jede positive Zahl \(\epsilon\):
\[\lim_{n\to\infty} P(|h_n-p|<\epsilon)=1\]
bzw. (gleichwertig)
\[\lim_{n\to\infty} P(|h_n-p|\geq\epsilon)=0\]
(Zum Beweis wird auf Kütting, 1999 verwiesen. Eine allgemeinere Version des schwachen Gesetzes der großen Zahlen findet sich z.B. bei Henze, 2018.)
Umgangssprachlich formuliert: Wächst \(n\) über alle Grenzen, dann strebt die Wahrscheinlichkeit, dass die relative Häufigkeit des Ereignisses \(A\) um weniger als eine beliebig kleine vorgegebene Zahl \(\epsilon\) von der tatsächlichen Wahrscheinlichkeit \(P(A)=p\) des Ereignisses \(A\) abweicht, gegen 1.

