Schulmathematik unter didaktischen Gesichtspunkten: Stochastik in der Sekundarstufe II (Demo-Kurs)
| Site: | WueCampus |
| Course: | vhb - Demokurs Lehramt |
| Book: | Schulmathematik unter didaktischen Gesichtspunkten: Stochastik in der Sekundarstufe II (Demo-Kurs) |
| Printed by: | Gästanvändare |
| Date: | Monday, 8 December 2025, 5:38 PM |
1. Wahrscheinlichkeitsrechnung
In diesem Modul werden die Grundlagen der Wahrscheinlichkeitsrechnung wiederholt und weiter vertieft. Eine zentrale Rolle spielen dabei die Konzepte der stochastischen Unabhängigkeit und der bedingten Wahrscheinlichkeit, die die Grundlage des bekannten Satzes von Bayes darstellen.
1.1. Lageparameter


Lageparameter
Definition (Arithmetisches Mittel)
\(x_1, x_2, \ldots , x_n\) seien Daten eines quantitativen Merkmals. Dann nennt man \[\overline{x} := \frac{x_1+x_2+\ldots + x_n}{n} = \frac{1}{n}\sum_{i=1}^n x_i\] deren arithmetisches Mittel.
Hinweise
- Die zur Berechnung des arithmetischen Mittels notwendigen Operationen lassen sich nur bei quantitativen Merkmalen durchführen.
- Durch Umformung obiger Gleichung ergibt sich: \[n\cdot\overline{x} = x_1+x_2+\ldots + x_n\] Die Summe aller \(n\) Einzelwerte kann man sich also durch die Summe von \(n\) gleich großen errechneten Werten \(\overline{x}\) ersetzt vorstellen. In diesem Sinne nimmt das arithmetische Mittel also eine Art Ersatzfunktion ein.
- Durch Umformung ergibt sich weiterhin, dass die Summe der Abweichungen aller Werte vom arithmetischen Mittel gleich Null ist: \[\sum_{i=1}^n (x_i-\overline{x}) = 0\]
- Das arithmetische Mittel wird stark von „Ausreißern“ beeinflusst, also von einzelnen Daten, die stark vom Rest der Daten abweichen.

Definition (Gewogenes arithmetisches Mittel)
\(x_1, x_2, \ldots , x_n\) seien Daten eines quantitativen Merkmals. Dann nennt man \[\overline{x} := \frac{g_1x_1+g_2x_2+\ldots + g_nx_n}{g_1+g_2+\ldots + g_n} = \frac{\sum_{i=1}^n g_ix_i}{\sum_{i=1}^n g_i}\]
mit \(g_i\geq 0\) für \(i=1,2,3,…,n\) und \(\sum_{i=1}^n g_i > 0\)
das gewogene arithmetische Mittel der Daten. Dabei werden die nichtnegativen Zahlen \(g_i\) als Gewichtungsfaktoren, bzw. Gewichtfaktoren bezeichnet. Sie weisen den einzelnen Werten ein höheres oder niedrigeres Gewicht zu. Alternativ ließe sich mit ganzzahligen \(g_i\) auch bestimmen, wie oft ein Datum \(x_i\) jeweils in der Messreihe vorkommt.

Definition (Geometrisches Mittel)
\(x_1, x_2, \ldots , x_n\) seien Daten eines quantitativen Merkmals mit \(x_i > 0\) für \(i=1,2,3,…,n\). Dann nennt man \[\overline{x}_g := \sqrt[n]{x_1\cdot x_2\cdot\ldots\cdot x_n}\] deren geometrisches Mittel.

Definition (Gewogenes geometrisches Mittel)
\(x_1, x_2, \ldots , x_n\) seien Daten eines quantitativen Merkmals mit \(x_i > 0\) für \(i=1,2,3,…,n\). Dann nennt man \[\overline{x}_g := \sqrt[G]{x_1^{g_1}\cdot x_2^{g_2}\cdot\ldots\cdot x_n^{g_n}} \text{ mit } G=\sum_{i=1}^n g_i\] deren gewogenes geometrisches Mittel.

Definition (Harmonisches Mittel)
\(x_1, x_2, \ldots , x_n\) seien Daten eines quantitativen Merkmals mit \(x_i > 0\) für \(i=1,2,3,…,n\). Dann nennt man \[\overline{x}_h := \frac{1}{\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n})}\] deren harmonisches Mittel.
Satz
\(x_1, x_2, \ldots , x_n\) seien metrische Daten mit \(x_i > 0\) für \(i=1,2,3,…,n\). Dann gilt:
\[\overline{x}_h\leq\overline{x}_g\leq\overline{x}\]
Dabei gilt das Gleichheitszeichen nur dann, wenn \(x_1=x_2=\ldots=x_n\)
Graphische Veranschaulichung der Ungleichung für \(\text{ }n=2\):
Für \(x_1\) und \(x_2\) gilt: \[\overline{x} = \frac{x_1+x_2}{2}\] \[\overline{x}_g = \sqrt{x_1\cdot x_2}\] \[\overline{x}_h = \frac{1}{\frac{1}{2}(\frac{1}{x_1}+\frac{1}{x_2})}\]
Damit gilt rechnerisch: \(\overline{x}_g^2 = \overline{x}_h\cdot \overline{x}\)
In einem Halbkreis mit Durchmesser \(x_1+x_2 = 2r\) hat der Radius gerade die Länge des arithmetischen Mittels \(\overline{x}\).
Nach dem Höhensatz gilt: \(\overline{x}_g^2 = x_1\cdot x_2 = h^2\). \(\overline{x}\) ist Hypotenuse des "inneren" Dreiecks, dessen eine Kathete \(\overline{x}_g\) ist. Nach obiger Rechnung gilt mit dem Kathetensatz: \[\overline{x}_h\cdot \overline{x} = \overline{x}_g^2 = m\cdot\overline{x},\] wobei \(m\) der längere der beiden Hypotenusen-Abschnitte ist.
Dementsprechend lassen sich die drei „Mittel“ (für \(n=2\) in ein rechtwinkliges Dreieck bzw. den zugehörigen Halbkreis einbeschreiben, anhand dessen sich leicht die obige Ungleichung graphisch belegen lässt.

Definition (Median)
Seien \(x_{(1)}\leq x_{(2)}\leq x_{(3)}\leq\ldots\leq x_{(n)}\) der Größe nach geordnete \(n\) Daten. Als Median wird die folgendermaßen definierte Zahl bezeichnet:
- Bei Daten von Rangmerkmalen \[x_{0,5} := \begin{cases} x_{(\frac{n+1}{2})} & \text{bei ungeradem } n \\ x_{(\frac{n}{2})}\text{ oder }x_{(\frac{n}{2}+1)} & \text{bei geradem } n \end{cases} \]
- Bei quantitativen nicht gruppierten Daten \[x_{0,5} := \begin{cases} x_{(\frac{n+1}{2})} & \text{bei ungeradem } n \\ \frac{1}{2}(x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)}) & \text{bei geradem } n \end{cases} \]
Die Schreibweise, Indizes in runde Klammern zu setzen, wird üblicherweise verwendet, um Daten zu kennzeichnen, die der Größe nach geordnet sind.
Für eine gerade Anzahl von Daten gibt es allerdings keine einheitliche Festlegung. Manchmal wird auch dabei das arithmetische Mittel aus \(x_{(\frac{n}{2})}\) und \(x_{(\frac{n}{2}+1)}\) gewählt, so wie dies bei quantitativen Merkmalen geschieht.
Der Median zeichnet sich dadurch aus, dass er in der „Mitte“ einer der Größe nach geordneten Datenmenge liegt. Dabei sind mindestens 50% der Daten kleiner oder gleich und mindestens 50% der Daten größer oder gleich dem Median.
Zur Bestimmung dieses Wertes werden lediglich die Rangmerkmale benötigt. Quantitative Merkmale werden nicht gebraucht.
Grafik zum Median
Satz (Minimumseigenschaft des Medians)
Seien \(x_1, x_2, \ldots , x_n\) quantitative Daten. Die Summe der absoluten Abweichungen aller Daten \(x_i\) von ihrem Median ist kleiner oder gleich der Summe aller absoluten Abweichungen der Daten \(x_i\) von irgendeinem anderen Wert \(c\), ist also ein Minimum. Es gilt:
\[\sum_{i=1}^n |x_i-x_{0,5}|\leq \sum_{i=1}^n |x_i-c| \text{ für beliebiges } c\in\mathbb{R}\]

Definition (p-Quantil)
Seien \(x_{(1)}\leq x_{(2)}\leq x_{(3)}\leq\ldots\leq x_{(n)}\) der Größe nach geordnete \(n\) Daten. Eine Zahl \(x_p\in\mathbb{R}\) heißt p-Quantil, falls gilt: Mindestens \(p\cdot 100\%\) der Daten liegen vor \(x_p\), und mindestens \((1-p)\cdot 100\%\) der Daten liegen nach \(x_p\).
Dann berechnet sich das p-Quantil durch: \[x_{p} := \begin{cases} x_{([np]+1)} & \text{ falls } np\text{ nicht ganzzahlig ist} \\ \frac{1}{2}(x_{(np)}+x_{(np+1)}) & \text{ falls } np\text{ ganzzahlig ist} \end{cases} \]
Dabei wird unter dem Symbol \([np]\) die größte ganze Zahl verstanden, die kleiner oder gleich \(np\) ist.
Hinweise
- Für \(p=0,5\) ergibt sich gerade der Median.
- p-Quantile kommen in der Praxis häufig vor. Dabei sind die folgenden Bezeichnungen üblich:
- \(x_{0,25}\) heißt erstes Quartil (auch unteres Quartil).
- \(x_{0,5}\) heißt zweites Quartil (Median).
- \(x_{0,75}\) heißt drittes Quartil (auch oberes Quartil).
- \(x_{0,1}\) heißt erstes Dezil.
- \(x_{0,9}\) heißt neuntes Dezil.

1.2. Streuungsparameter


Definition (Spannweite)
Als Spannweite (oder Variationsbreite) wird die Differenz \(SW=x_{max}-x_{min}\) zwischen dem größten (den wir \(x_{max}\) nennen) und dem kleinsten (den wir \(x_{min}\) nennen) Merkmalswert einer geordneten Datenmenge bezeichnet.
Da die Spannweite nur vom größten und kleinsten Wert der Datenmenge bestimmt wird, hängt sie stark von Ausreißern ab und gibt keine Auskunft darüber, wie sich die Werte im Intervall \([x_{min},x_{max}]\) verhalten. Die Spannweite ändert sich nur, wenn ein neuer Wert auftritt, der kleiner als \(x_{min}\) oder größer als \(x_{max}\) ist.

Definition (Quartilsabstand)
\(x_{(1)},x_{(2)},x_{(3)},\ldots ,x_{(n)}\) seien geordnete Daten. Die Differenz \(QA=x_{0,75}-x_{0,25}\) zwischen dem oberen (dritten) Quartil \(x_{0,75}\) und dem unteren (ersten) Quartil \(x_{0,25}\) heißt Quartilsabstand QA.
Während die Spannweite also einen Bereich festlegt, innerhalb dessen \(100\%\) der Merkmalswerte liegen, wird durch den Quartilsabstand ein Bereich festgelegt, der \(50\%\) aller Messwerte beinhaltet und in dem insbesondere der Median \(x_{0,5}\) liegt.
Per Definition liegt der Median immer in diesem Bereich. Bei asymmetrischen Verteilungen allerdings liegt er nicht in der Mitte des Quartilsintervalls \([x_{0,25},x_{0,75}]\).
Durch den Quartilsabstand wird die Datenmenge in drei Bereiche eingeteilt:
- \(25\%\) der Werte, die kleiner sind als das untere Quartil
- \(50\%\) der Werte, die im Intervall \([x_{0,25},x_{0,75}]\) liegen
- \(25\%\) der Werte, die größer sind als das obere Quartil
Eine graphische Darstellungsweise, die z.B. in wissenschaftlichen Publikationen verwendet wird, ist das Box-Plot-Diagramm.

Definition Mittlere (lineare) absolute Abweichung
\(x_1, x_2, \ldots , x_n\) seien Ausprägungen eines quantitativen Merkmals und \(\overline{x}\) deren arithmetisches Mittel. Dann heißt
\[d_{\overline{x}} := \frac{1}{n}\sum_{i=i}^n |x_i-\overline{x}| = \frac{1}{n}(|x_1-\overline{x}|+\ldots+|x_n-\overline{x}|)\]
die mittlere (lineare) absolute Abweichung vom arithmetischen Mittel \(\overline{x}\).
Analog lässt sich auch die mittlere absolute Abweichung vom Median definieren:
\[d_{x_{0,5}} := \frac{1}{n}\sum_{i=i}^n |x_i-x_{0,5}| = \frac{1}{n}(|x_1-x_{0,5}|+\ldots+|x_n-x_{0,5}|)\]
Der Betrag bzw. die Wahl der absoluten Abweichung in der obigen Definition trägt der Tatsache Rechnung, dass die Summe aller Abweichungen vom arithmetischen Mittel gleich Null ist.

Empirische Varianz, empirische Standardabweichung

Definition (Empirische Varianz)
\(x_1, x_2, \ldots , x_n\) seien Ausprägungen eines quantitativen Merkmals und \(\overline{x}\) deren arithmetisches Mittel. Dann heißt
\[s^2 := \frac{1}{n-1}\sum_{i=i}^n (x_i-\overline{x})^2, n\geq 2\]
die empirische Varianz \(s^2\).

Definition (Empirische Standardabweichung)
\(x_1, x_2, \ldots , x_n\) seien Ausprägungen eines quantitativen Merkmals und \(\overline{x}\) deren arithmetisches Mittel. Dann heißt
\[s := \sqrt{\frac{1}{n-1}\sum_{i=i}^n (x_i-\overline{x})^2}, n\geq 2\]
empirische Standardabweichung.
Bei der empirischen Varianz handelt es sich um das arithmetische Mittel der quadratischen Abweichungen vom arithmetischen Mittel. Handelt es sich bei den zu Grunde liegenden Daten bspw. um Körpergrößen in cm, dann misst die Varianz die Abweichung in Quadratzentimetern. Die Standardabweichung hingegen misst wieder in der ursprünglichen Maßeinheit.
Anmerkungen/Hinweise:
- Im Rahmen der Schätztheorie in der Sekundarstufe II kann begründet werden, dass die so definierte Varianz \(s^2\) mit dem Faktor \(\frac{1}{n-1}\) ein erwartungstreuer Schätzer für die Varianz \(\sigma^2\) ist. \(\frac{1}{n}\sum_{i=i}^n (x_i-\overline{x})^2\) hingegen würde diese Eigenschaft nicht erfüllen.
- Allerdings findet sich die Definition mit dem Faktor \(\frac{1}{n}\) anstatt \(\frac{1}{n-1}\) in der (didaktischen) Literatur. Auf Taschenrechnern (bzw. häufig auch bei CAS-Rechnern) sind oft beide Implementationen vorhanden. Deshalb sollte überprüft werden, welche Definition verwendet wird.
- Bei großem Stichprobenumfang ist der Unterschied zwischen Division durch \(n\) und durch \(n-1\) allerdings unerheblich.
- In Anwendungen (z.B. in den Naturwissenschaften) werden arithmetisches Mittel und Standardabweichung häufig nicht getrennt angegeben, sondern in der Form \(\overline{x}\pm s\).
Liegen annähernd normalverteilte Daten vor, so gilt:
- Ca. \(68\%\) der Daten liegen im Bereich \(\overline{x}\pm s\), das heißt, im Intervall zwischen \(\overline{x}-s\) und \(\overline{x}+s\).
- Ca. \(96\%\) der Daten liegen im Bereich \(\overline{x}\pm 2s\).
- Ca. \(99\%\) der Daten liegen im Bereich \(\overline{x}\pm 3s\).
Anschaulich interpretiert, weichen also ungefähr \(68\%\), bzw. \(96\%\) bzw. \(99\%\) der Daten um höchstens eine Standardabweichung, bzw. um zwei Standardabweichungen, bzw. um drei Standardabweichungen vom Mittelwert ab.
Dies steht in Beziehung zu den drei Sigma-Regeln, die im Kapitel zur Normalverteilung behandelt werden (vgl. Kapitel 5.2).

1.3. Allgemeine Wahrscheinlichkeitsräume

Allgemeine Wahrscheinlichkeitsräume
Aus der Sekundarstufe I ist der Umgang mit Wahrscheinlichkeitsräumen bekannt bzw. deren implizite Verwendung. Die dabei relevanten Wahrscheinlichkeitsräume zeichnen sich durch die Endlichkeit ihrer Ergebnismenge \(\Omega \) aus:

Definition (Endlicher Wahrscheinlichkeitsraum)
Sei \(\Omega \) eine endliche, nichtleere Ergebnismenge und sei \(P\colon\wp (\Omega)\longrightarrow\mathbb{R}\) eine Abbildung von der Potenzmenge \(\wp (\Omega)\) in die reellen Zahlen. Dann heißt \(P\) ein Wahrscheinlichkeitsmaß auf \(\Omega \), falls die folgenden drei Axiome erfüllt sind:
Kolmogoroff-Axiome:
-
(Nichtnegativität) \(P(A)\geq 0\) für alle \(A\in\wp (Ω)\)
Das heißt: Jedem Ereignis \(A\) wird durch die Abbildung \(P\) eindeutig eine nichtnegative reelle Zahl \(P(A)\) zugeordnet.
-
(Normierung) \(P(\Omega ) = 1\)
Das heißt: Dem sicheren Ereignis \(\Omega \) wird die Zahl \(1\) zugeordnet.
-
(Additivität) \(P(A\cup B)=P(A)+P(B) \) für alle disjunkten Ereignisse \(A, B\in\wp (Ω)\)
Das heißt: Für disjunkte Ereignisse \(A\) und \(B\) ist die Wahrscheinlichkeit \(P(A\cup B)\), dass \(A\) oder \(B\) oder \(A\) und \(B\) eintreten, gleich der Summe der Einzel-Wahrscheinlichkeiten: \(P(A)+P(B) \).
Ist ein derartiges Wahrscheinlichkeitsmaß \(P\) auf \(\Omega\) gegeben, dann heißt \((\Omega, \wp (\Omega), P )\) endlicher Wahrscheinlichkeitsraum.
Durch die Einführung des Konzepts Wahrscheinlichkeitsraum wird die bisher anschaulich motivierte Vorstellung der Wahrscheinlichkeit theoretisch fundiert und axiomatisiert. Kolmogoroffs Axiomensystem stellt zuerst einmal „nur“ ein mögliches System von Verknüpfungen dar, aus dem sich allerdings die bekannten Eigenschaften, die vom Wahrscheinlichkeitsbegriff erwartet werden, ableiten lassen. Das System ist dabei effizient – es enthält so wenige Axiome wie möglich – und diese Axiome sind widerspruchsfrei.
Im Folgenden wird dieses Konzept verallgemeinert, hin zu Wahrscheinlichkeitsräumen mit abzählbar-unendlicher Ergebnismenge \(\Omega\).
Analog zum Fall des endlichen Wahrscheinlichkeitsraums wird dabei jedem Elementarereignis \(\{\omega_i\}\) aus \(\Omega = \{\omega _1, \omega _2, \omega _3, \ldots \}\) eine nichtnegative Zahl \(P(\omega _i)\) zugeordnet, sodass die Summe aller solchen Wahrscheinlichkeiten 1 ergibt: \(\sum_{i=1}^{\infty}{P(\omega_i) = 1}\)
Für alle Teilmengen \(E\) von \(\Omega\) wird dann die eine Wahrscheinlichkeitsverteilung P definiert durch: \(P(E)=\sum_{\omega_i\in E}{P(\omega_i)}\)
Da diese Summe absolut konvergent ist (also jede Umordnung gegen den gleichen Wert konvergiert), ist die Wahrscheinlichkeitsverteilung wohldefiniert.

Definition (Abzählbar-unendlicher Wahrscheinlichkeitsraum)
Sei \(\Omega \) eine abzählbar-unendliche, nichtleere Ergebnismenge. Eine Funktion
\[P\colon\wp (\Omega)\longrightarrow\mathbb{R}\text{ mit } A\mapsto P(A)\text{ für } A\in\wp (Ω)\]
heißt Wahrscheinlichkeitsmaß auf \(\Omega \), falls gilt:
Kolmogoroff-Axiome:
-
(Nichtnegativität) \(P(A)\geq 0\) für alle \(A\in\wp (Ω)\)
Das heißt: Jedem Ereignis \(A\) wird durch die Abbildung \(P\) eine nichtnegative reelle Zahl \(P(A)\) zugeordnet.
-
(Normierung) \(P(\Omega ) = 1\)
Das heißt: Dem sicheren Ereignis \(\Omega \) wird die Zahl \(1\) zugeordnet.
-
(\(\sigma \)-Additivität) Für ein System von Mengen \(A_i\in\wp (Ω) (i\in\mathbb{N}\) mit \(A_i\cap A_j =\emptyset\) für \(i\neq j\) gilt:
\[P(\bigcup_{i=1}^\infty A_i )=\sum_{i=1}^\infty P(A_i) \]
Das heißt, dass für abzählbar-unendlich viele, paarweise disjunkte Mengen \(A_i (i\in\mathbb{N})\) das Wahrscheinlichkeitsmaß der Vereinigung dieser Mengen gleich der Summe der Wahrscheinlichkeitsmaße der einzelnen Mengen ist.
In diesem Fall nennt man \((\Omega, \wp (\Omega), P )\) einen abzählbar-unendlichen Wahrscheinlichkeitsraum.
Im Gegensatz zu endlichen Wahrscheinlichkeitsräumen, wo nur die Wahrscheinlichkeit der Vereinigung endlich vieler, paarweise disjunkter, Mengen erklärt ist, ist im Fall des abzählbar-unendlichen Wahrscheinlichkeitsraums die Wahrscheinlichkeit der Vereinigung abzählbar-unendlich vieler, paarweise disjunkter, Mengen erklärt.
In beiden Fällen spricht man von sogenannten diskreten Wahrscheinlichkeitsräumen. (In Kapitel 5 hingegen werden Wahrscheinlichkeitsräume mit überabzählbar-unendlicher Ergebnismenge \(\Omega\) benötigt.)
Beispiel – „Warten auf die erste 6“
Eine abzählbar-unendliche Ergebnismenge wird bspw. im Fall des „Wartens auf den ersten Erfolg“ benötigt. Wird beim Würfelspiel mir einem regulären Würfel so lange gewürfelt, bis zum ersten Mal eine Sechs fällt, dann ergibt sich als Ergebnismenge \(\Omega=\{1,2,3,\ldots\}\) die Menge der Nummern der Versuche, in denen zum ersten Mal eine Sechs geworfen wird. Diese muss die ganze Menge der natürlichen Zahlen sein, da der Wurf der ersten Sechs theoretisch beliebig „spät“ erfolgen kann.
Bei diesem Experiment beträgt die Wahrscheinlichkeit, im i-ten Versuch die erste 6 zu würfeln: \(P(\omega_i)=\Big(\frac{5}{6}\Big)^{i-1}\cdot\frac{1}{6}\). Auf Grund der geometrischen Summenformel \(1+q+q^2+\ldots + q^n = \frac{1-q^{n+1}}{1-q}\) gilt: \[ \sum_{i=1}^{\infty}{P(\omega_i)}=\sum_{i=1}^{\infty}{\Big(\frac{5}{6}\Big)^{i-1}\cdot\frac{1}{6}}= \frac{1}{6}\cdot\sum_{i=1}^{\infty}{\Big(\frac{5}{6}\Big)^{i}} = \frac{1}{6}\cdot\frac{1}{1-\frac{5}{6}}=1 \]

1.4. Bedingte Wahrscheinlichkeiten und stochastiche Unabhängigkeit

Ein zentrales Ziel der Wahrscheinlichkeitslehre/Stochastik ist die Berechnung von („neuen“) Wahrscheinlichkeiten unter Verwendung bereits bekannter Wahrscheinlichkeiten.
So lassen sich beispielsweise viele komplexere Zufallsexperimente als Verkettung von einfacheren Zufallsexperimenten beschreiben, die dann als mehrstufige Zufallsexperimente bezeichnet werden.
So könnte bspw. das Werfen von drei Würfeln als dreimaliges Werfen des gleichen Würfels interpretiert werden. (Hierbei darf allerdings die Reihenfolge der Würfelergebnisse keine Rolle spielen!)
Im Fall der sogenannten bedingten Wahrscheinlichkeiten stellt sich die Frage, ob und wie sich zwei Ereignisse gegenseitig beeinflussen bzw. ob diese voneinander (stochastisch) unabhängig sind. Es stellt sich also die Frage, ob sich die Wahrscheinlichkeit für das Eintreten eines Ereignisses \(B\) ändert, wenn bereits bekannt ist, dass ein anderes Ereignis A eingetreten ist.

Beispiel
Im Fall einer Grippe-Impfung (Ereignis \(A\)) stellt sich die Frage, ob diese (so wie gewünscht) das Eintreten des Ereignisses \(B\) „Grippeerkrankung“ verringert.
Es interessiert also die Wahrscheinlichkeit, dass \(B\) eintritt unter der Bedingung, dass \(A\) eingetreten ist, was zum Begriff der Bedingten Wahrscheinlichkeit führt:
\[P(B│A)=P_A (B)\]
Da vorerst unklar ist, wie sich ein solcher qualitativer Zusammenhang quantifizieren lässt, soll dieser hergeleitet werden. Dazu wird das Laplace-Modell als Grundlage verwendet.
Die Ergebnisse einer Studie zur Wirksamkeit von Grippeschutzimpfungen werden in der folgenden Vierfelder-Tafel dargestellt:
| erkrankt | nicht erkrankt | ||
|---|---|---|---|
| geimpft | 117 | 389 | 506 |
| nicht geimpft | 289 | 165 | 454 |
| 406 | 554 | 960 |
Dabei wurden 960 Personen untersucht und die Befunde (s. Tabelle) auf entsprechenden Datenkarten notiert. Wird aus der Menge dieser Karten zufällig eine gezogen, dann lassen sich aus der Tabelle die entsprechenden „möglichen“ und „günstigen“ Fälle ablesen.
Für den Fall \(A\) – geimpft und \(B\) – hatte Grippe ergibt sich: \[P(A)=\frac{506}{960}\approx 53\%, P(B)=\frac{406}{960}\approx 43\%\] Die Ergebnismenge \(\Omega\) besteht dabei aus den 960 Datenkarten, \(A\) aus den 506 Karten der geimpften Personen und \(B\) aus den 406 Karten der erkrankten Personen.
Entsprechend ergeben sich auch die Laplace-Wahrscheinlichkeiten für andere Ereignisse:
\(P(\overline{A})=\frac{454}{960}\approx 47\%\), wobei \(\overline{A}\) das Gegenereignis „nicht geimpft“ von \(A\) ist, und
\(P(A\cap B)=\frac{117}{960}\approx 12\%\), wobei \(A\cap B\) für das Ereignis „geimpft und erkrankt“ steht
Mit der Frage „Aus \(\Omega\) wird eine geimpfte Person gezogen. Mit welcher Wahrscheinlichkeit ist diese an Grippe erkrankt?“ wird eine bedingte Wahrscheinlichkeit beschrieben, die sich durch die entsprechende Laplace-Wahrscheinlichkeit \(P(B│A)\) modellieren lässt.
Als „mögliche“ Fälle kommen nunmehr nur die 506 geimpften Personen in Frage, als „günstige“ Fälle die 117 geimpften und erkrankten Personen. Daher gilt:
\[P(B│A)=\frac{117}{506}\approx 23\%\]
Mit Hilfe des Laplace-Ansatzes ergibt sich dann:
\(P(B│A)=\frac{|A∩B|}{|A|} = \frac{\frac{|A\cap B|}{|\Omega|}}{\frac{|A|}{|Ω|}}=\frac{P(A\cap B)}{P(A)}\)
Damit wurde die Wahrscheinlichkeit \(P(B│A)\) mit Hilfe von Werten der Wahrscheinlichkeitsverteilung \(P\) ausgedrückt.

Definition (Bedingte Wahrscheinlichkeiten)
Seien \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum und \(B\) ein Ereignis mit \(P(B)>0\). Dann heißt
\(P(A│B)≔\frac{P(A∩B)}{P(B)}\)
bedingte Wahrscheinlichkeit von \(A\) unter der Bedingung \(B\). Alternativ wird die Schreibweise \(P_B (A)\) verwendet.

Satz
Seien \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum und \(B\) ein Ereignis mit \(P(B)>0\). Dann ist die Funktion
\[P(*│B)\colon P(\Omega)\longrightarrow\mathbb{R}^{\geq 0}\]
mit
\[P(A│B):= \frac{P(A∩B)}{P(B)}\]
die jedem Ereignis \(A\in P(\Omega)\) die Wahrscheinlichkeit \(P(A│B)\) zuordnet, ein Wahrscheinlichkeitsmaß auf \(P(\Omega)\).
Hinweise:
- Auch bei den bislang in diesem Kurs untersuchten Wahrscheinlichkeiten \(P(A)\) handelt es sich um bedingte Wahrscheinlichkeiten. Es gilt \[P(A│\Omega):=\frac{P(A\cap\Omega)}{P(\Omega)} =\frac{P(A)}{1}=P(A)\] für alle \(A\in P(\Omega)\)
- Mit \(A|B\) wird keine Teilmenge von \(\Omega\) beschrieben. \(A|B\) ist also kein Ereignis und tritt nie eigenständig auf, sondern nur in Verbindung mit \(P(A│B)\) – der bedingten Wahrscheinlichkeit von \(A\) unter der Bedingung von \(B\). Die damit verbundene Interpretations-Schwierigkeit wird mit der Schreibweise \(P_B (A)\) gemindert.
- Für alle Ereignisse \(A\neq\emptyset\) mit \(P(A)>0\) gilt \(P(A|A)=1\), denn
\(P(A│A)≔\frac{P(A\cap A)}{P(A)} = \frac{P(A)}{P(A)} = 1\) - Für \(P(B)=0\) ergibt die Definition \(\frac{P(A∩B)}{P(B)}\) keinen Sinn.
- Gilt für \(A\) und \(B\) mit \(P(B)>0\), dass \(P(A\cap B)=0\), dann ist per Definition \(P(A│B)=0\).
- Durch Umformen der Definition ergibt sich die folgende Regel für Wahrscheinlichkeiten von Ereignissen der Form \(A\cap B\) für \(P(B)>0\):
\[P(A\cap B)=P(B)\cdot P(A│B)\]
Da \((A\cap B)=(B\cap A)\), ist aus Symmetriegründen auch für \(P(A)>0\)
\[P(A\cap B)=P(A)\cdot P(B│A)\] - Während (s. 4)) für \(P(B)=0\) die Definition der bedingten Wahrscheinlichkeit \(\frac{P(A∩B)}{P(B)}\) keinen Sinn ergibt, ist es dennoch sinnvoll, für die Multiplikationsregeln aus 6) zu vereinbaren, dass \(P(A\cap B)=0\) gelten soll, falls \(P(A)=0\) oder \(P(B)=0\) ist.

Stochastische Unabhängigkeit
Im vorherigen Anwendungs-Beispiel wird, inhaltlich gesehen, davon ausgegangen bzw. gehofft, dass Ereignis \(A\) (die Grippe-Impfung) Ereignis \(B\) (eine Grippe-Erkrankung) beeinflusst (also das Risiko einer solchen verringert).
In anderen Fällen beeinflussen sich Ereignisse hingegen nicht, bzw. sollen sich nicht gegenseitig beeinflussen, also voneinander unabhängig sein. Es soll dann also gelten: \[P(B)=P(B│A)\]. Dabei ist zu bemerken, dass die Forderung \(P(A)≠0\) keine Einschränkung darstellt. \(P(A)=0\) entspräche einem Nicht-Eintreten von \(A\). Die bedingte Wahrscheinlichkeit von \(B\) bei Eintreten von \(A\) wäre damit nicht sinnvoll (vgl. Hinweis 4 oben).
Ist also \(P(B)=P(B│A)\), dann gilt unter Verwendung der Formel für die Berechnung der bedingten Wahrscheinlichkeit aus: \[P(B)=P(B│A)= \frac{P(A\cap B)}{P(A)}\] Umformen führt zur folgenden Definition:

Definition (Stochastische Unabhängigkeit)
\((\Omega, \wp (\Omega), P )\) sei ein Wahrscheinlichkeitsraum. Zwei Ereignisse \(A\) und \(B\) werden als stochastisch unabhängig bezeichnet, wenn gilt:
\[P(A)\cdot P(B)=P(A\cap B)\] Sonst heißen \(A\) und \(B\) stochastisch abhängig.
Diese Definition ist rechnerisch handhabbar, zeigt die Symmetrie der „Beziehung“ und ist auch für die Fälle \(P(A)=0\) oder \(P(B)=0\) gültig.
Hinweis:
Sind \(A\) und \(B\) unabhängig, dann sind die folgenden Ereignisse jeweils unabhängig:
- \(A\) und \(\overline{B}\)
- \(\overline{A}\) und \(B\)
- \(\overline{A}\) und \(\overline{B}\)
Ob zwei Ereignisse \(A\) und \(B\) stochastisch unabhängig sind, lässt sich mittels einer Vierfeldertafel überprüfen.
| \(P(B)\) | \(P(\overline{B})\) | |
|---|---|---|
| \(P(A)\) | \(P(A\cap B)\) | \(P(A\cap \overline{B})\) |
| \(P(\overline{A})\) | \(P(\overline{A}\cap B)\) | \(P(\overline{A}\cap \overline{B})\) |
Sind \(A\) und \(B\) stochastisch unabhängig, so müssen die Werte in obiger Tafel mit denen der folgenden Multiplikationstafel übereinstimmen.
| \(P(B)\) | \(P(\overline{B})\) | |
|---|---|---|
| \(P(A)\) | \(P(A)\cdot P(B)\) | \(P(A)\cdot P(\overline{B})\) |
| \(P(\overline{A})\) | \(P(\overline{A})\cdot P(B)\) | \(P(\overline{A})\cdot P(\overline{B})\) |
Qualitativ betrachtet lässt sich sagen: Je stärker die Zahlenwerte differieren, desto größer ist die inhaltliche Abhängigkeit der Ereignisse.

1.5. Satz von Bayes


Satz (Totale Wahrscheinlichkeit)
Ist \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum und bilden die Ereignisse \(B_1, B_2, \ldots , B_n\) von \(\Omega\) mit \(P(B_k)>0\) für alle \(k = 1, 2, \ldots , n\) eine Zerlegung von \(\Omega\), ist also:
- \(B_1\cup B_2\cup \ldots\cup B_n = \Omega\) und
- \(B_i\cap B_j= \emptyset\), für alle \(i\neq j,\)
dann gilt für jedes Ereignis \(A \in\wp (\Omega)\): \[P(A) = P(B_1)\cdot P(A|B_1)+P(B_2)\cdot P(A|B_2)+\ldots + P(B_n)\cdot P(A|B_n)\] \[P(A) = \sum_{k=1}^n P(B_k)\cdot P(A|B_k)\]
Für den Sonderfall \(n=2\) ergibts sich damit:
Die Ergebnismenge \(\Omega\) zerfällt nur in \(B\) und \(\overline{B}\), also \(\Omega = B\cup \overline{B}\). Für \(P(B)>0\) und \(P(\overline{B})>0\) gilt dann: \[P(A) = P(B)\cdot P(A|B) + P(\overline{B})\cdot P(A|\overline{B})\]

Satz (Satz von Bayes)
Es seien \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum und \(A\) ein Ereignis mit \(P(A)>0\). Bilden die Ereignisse \(B_1, B_2, \ldots , B_n\) von \(\Omega\) mit \(P(B_k)>0\) für alle \(k = 1, 2, \ldots , n\) eine Zerlegung von \(\Omega\), dann gilt für jedes \(k = 1, 2, \ldots , n\): \[P(B_k|A)=\frac{P(B_k)\cdot P(A|B_k)}{P(A)} = \frac{P(B_k)\cdot P(A|B_k)}{\sum_{k=1}^n P(B_k)\cdot P(A|B_k)}\]
Für den Sonderfall \(n=2\) ergibts sich damit:
Die Ergebnismenge \(\Omega\) zerfällt nur in \(B\) und \(\overline{B}\), also \(\Omega = B\cup \overline{B}\). Für \(P(B)>0\) und \(P(\overline{B})>0\) gilt dann: \[P(B|A) = \frac{P(B)\cdot P(A|B)}{P(B)\cdot P(A|B) + P(\overline{B})\cdot P(A|\overline{B})} \]
Didaktische Hinweise:
- Der Satz von Bayes lässt sich aus Umformungen der Definitionsgleichung der bedingten Wahrscheinlichkeit herleiten und muss deshalb im Prinzip nicht auswendig gelernt werden. Zum Beweis sei z.B. auf die Literatur verwiesen.
- Für den Sonderfall \(n=2\), bei dem die Ereignismenge \(\Omega\) nur in die Ereignisse in \(B\) und \(\overline{B}\) zerfällt, lässt sich die totale Wahrscheinlichkeit \(P(A)\) für ein Ereignis \(A\) gut mittels Baumdiagramm bestimmen:
Dabei müssen die beiden bei A endenden Pfade berücksichtigt und die Multiplikations- und Additionsregeln angewendet werden: \[P(A) = P(B)\cdot P(A|B) + P(\overline{B})\cdot P(A|\overline{B})\]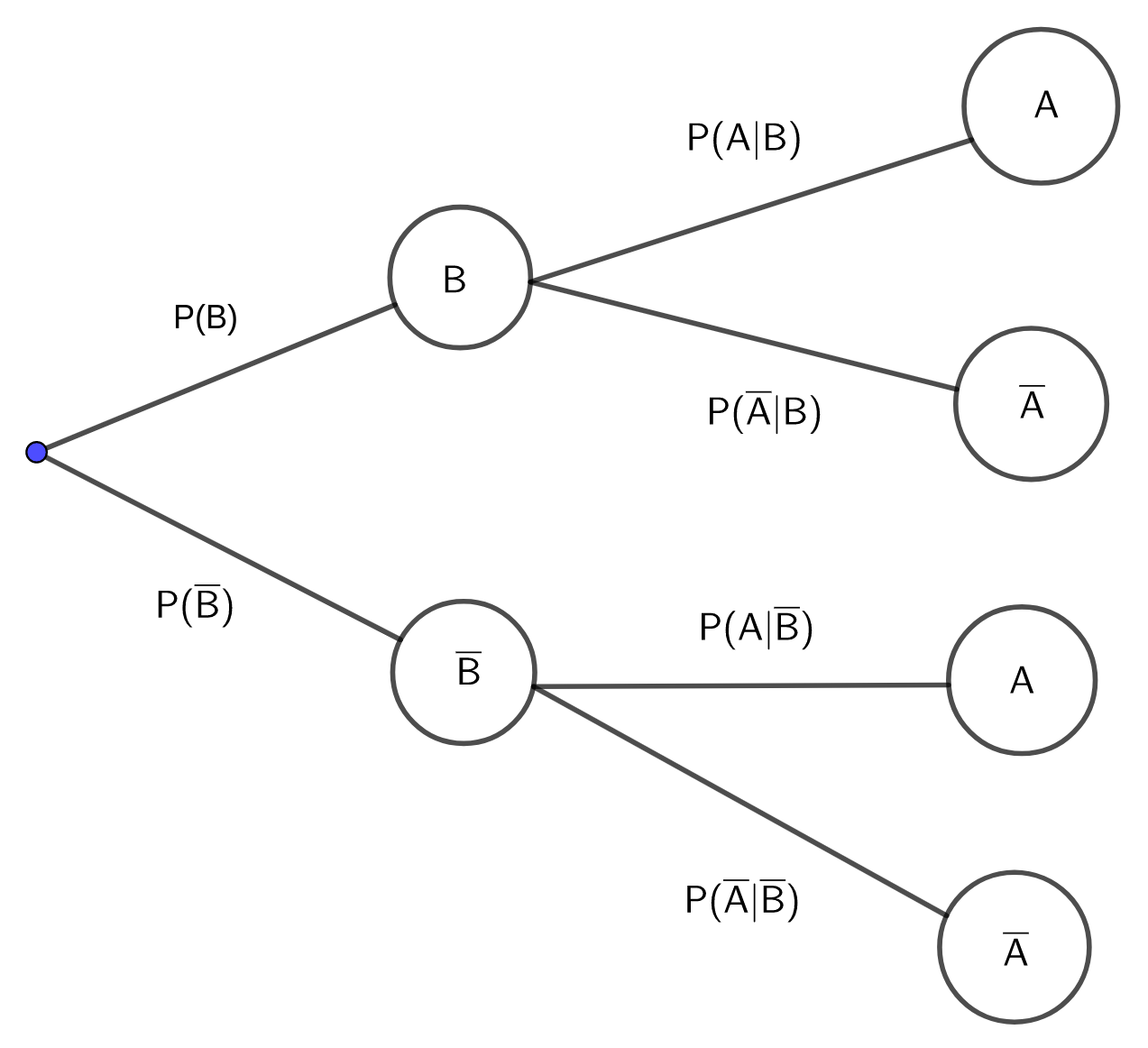
- Soll die Formel von Bayes angewendet werden, wird zur Berechnung von \(P(B_k|A)\) auch Kenntnis über \(P(B_k)\) benötigt. \(P(B_k)\) wird als a-priori-Wahrscheinlichkeit für das Ereignis \(B_k\) bezeichnet, \(P(B_k|A)\) als a-posteriori-Wahrscheinlichkeit für \(B_k\).
Beispiel (Mordprozess)
Bei einem Mordprozess liegen Indizien vor, die für die Täterschaft einer bestimmten Person sprechen. Als ein solches Indiz (Ereignis \(A\) käme bspw. die „Übereinstimmung der Blutgruppe bei Blutspuren an der Kleidung der verdächtigen Person und der des Opfers“ in Frage oder die „Übereinstimmung von Textilfaserspuren an der Kleidung der verdächtigen Person und der des Opfers“.
Mit \(B\) werde das Ereignis bezeichnet, dass der Verdächtige Kontakt mit dem Opfer hatte.
Es interessiert also die Frage nach der Wahrscheinlichkeit \(P(B|A)\), dass also die verdächtige Person Kontakt mit dem Opfer hatte, unter der Bedingung, dass ein Indiz \(A\) erfüllt ist.
Mit der Formel von Bayes liegt hierfür eine Berechnungsmöglichkeit vor. Allerdings müssen dafür auch \(P(A|B)\), \(P(A)\) und \(P(B)\) bekannt sein. Gerade über letztere a-priori-Wahrscheinlichkeit \(P(B)\) ist oft wenig bekannt. Deshalb müssen Annahmen gemacht werden.
Für \(P(A|B)\) ließe sich annähernd \(1\) annehmen, denn es lässt sich mit an Sicherheit grenzender Wahrscheinlichkeit annehmen, dass sich unter der Hypothese eines Kontaktes \(B\) Indizien der zuvor beschrieben Art ergeben.
Zur Bestimmung von \(P(A)\) wird auch \(P(A|\overline{B})\) benötigt. Um diese Wahrscheinlichkeit abzuschätzen könnte man beim Indiz „Blutspuren“ die prozentuale Häufigkeit der Blutgruppe des Opfers in der Bevölkerung annehmen.
Wie sieht es allerdings mit der a-priori-Wahrscheinlichkeit \(P(B)\) („Verdächtige Person hatte Kontakt mit dem Opfer“) aus?
Eine sehr gewagte Vorgehensweise ist die eines Gutachters, der sich bei einem Mordprozess 1973/74 folgendermaßen entschied: „Ich nehme eine a-priori-Wahrscheinlichkeit von 50% für die Täterschaft des Beklagten an. Das bedeutet, dass ich ihm gegenüber unvoreingenommen bin – ich gehe davon aus, dass er ebenso schuldig wie unschuldig sein kann.“
Dieses mathematische Modell ist als unangemessen zu verwerfen! Eine solche Vorgehensweise ließe sich in einem Fall unterstützen, in dem bspw. eine von zwei Personen mit Sicherheit der Täter ist. Im Vorliegenden Fall allerdings ist die Annahme einer a-priori-Wahrscheinlichkeit von 50% für die Täterschaft unrealistisch und darf nicht verwendet werden. Eine wesentlich kleinere a-priori-Wahrscheinlichkeit wäre angemessener.
Im konkreten Mordprozess hatte der Gutachter dementsprechend eine über 90%-ige Wahrscheinlichkeit für die Täterschaft des Angeklagten errechnet. Auf Grund eines Alibis wurde dieser allerdings freigesprochen und der Prozess abgebrochen. Hieran lässt sich leicht erkennen, dass Modellannahmen leicht zu Fehlbeurteilungen führen können.
Beispiel (Medizinischer Test - "False Positives")
Ein medizinischer Test zur Früherkennung einer bestimmten Krankheit liefert bei erkrankten Personen in 96% der Fälle auch einen positiven Krankheitsbefund. Andererseits liefert dieser Test auch bei gesunden Personen in 3% der Fälle einen positiven Krankheitsbefund („falsch-positiv“).
Es wird angenommen, dass die betreffende Krankheit in der zu Grunde liegenden Population (Grundgesamtheit) bei 2% der Personen vorliegt.
Es ergeben sich also vor allem die folgenden Fragestellungen:
- Wie groß ist die Wahrscheinlichkeit, dass eine zufällig „gezogene“ Person der Grundgesamtheit beim Test einen positiven Krankheitsbefund erhält?
- Wie groß ist die Wahrscheinlichkeit, dass eine zufällig aus der Gruppe der positiv getesteten Personen „gezogene“ Person tatsächlich Träger der Krankheit ist?
- Wie groß ist die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person mit positivem Befund eigentlich gesund ist?
Wir definieren die folgenden Ereignisse:
- \(K:\) "Person ist krank"
- \(\overline{K}:\) "Person ist gesund"
- \(T:\) "Untersuchungsbefund ist positiv"
- \(\overline{T}:\) "Untersuchungsbefund ist negativ"
Unter den Modellannahmen der Aufgabe gilt: \[P(K)=0.02; P(T|K) = 0.96; P(T|\overline{K})=0.03\]
- Gesucht ist die totale Wahrscheinlichkeit \(P(T)\): \[\begin{align} P(T) &= P(K)\cdot P(T|K)+P(\overline{K})\cdot P(T|\overline{K}) \\ &= 0.02\cdot 0.96 + (1-0.02)\cdot 0.03 = 0.0486 \end{align}\]
- Gesucht ist die bedingte Wahrscheinlichkeit \(P(K|T)\), die sich mit der Formel von Bayes berechnen lässt: \[P(K|T) = \frac{P(K\cap T)}{P(T)} = \frac{P(K)\cdot P(T|K)}{P(T)}\] Mit a. folgt: \[P(K|T) = \frac{0.02\cdot 0.96}{0.0486} \approx 0.3951\]
- Gesucht ist die bedingte Wahrscheinlichkeit \(P(\overline{K}|T)\). \[P(\overline{K}|T) = \frac{P(\overline{K})\cdot P(T|\overline{K})}{P(T)} = \frac{0.98\cdot 0.03}{0.0486} \approx 0.6049\] Die Lösung von c. lässt sich allerdings leichter bestimmen durch: \[P(\overline{K}|T) = 1 - P(K|T) = 1-0.3951 = 0.6049\]
Anmerkungen:
- Die Annahme, dass die betreffende Krankheit bei 2% der Personen der Grundgesamtheit auftritt (\(P(K) = 0.02\)), geht entscheidend in alle obigen Lösungen ein – bspw. in Teil b) bei der Berechnung der a-posteriori-Wahrscheinlichkeit \(P(K|T)\).
Diese a-priori-Wahrscheinlichkeit \(P(K)\) wurde vermutlich als Schätzwert mittels relativer Häufigkeiten gefunden. Dies wirft Fragen auf: Wie groß war die untersuchte Menge an Personen? Wie homogen/inhomogen war diese? Wurden dabei Personen aus Risikogruppen berücksichtigt? Dadurch wird deutlich, dass die Lösungen im Beispiel nur Lösungen unter bestimmten Modellannahmen sind! - Mit den obigen Bezeichnungen lautet eine geeignete Ergebnismenge \(\Omega\): \[\Omega = \{(K, T), (K, \overline{T}), (\overline{K}, T), (\overline{K}, \overline{T}) \}\] Dabei bedeutet das Ereignis \(\{(\overline{K}, T), (\overline{K}, \overline{T})\}\): „Person ist gesund“
- Auch bei dieser Aufgabenstellung lässt sich die Vierfeldertafel wirkungsvoll zur Unterstützung einsetzen. Das Untersuchungskollektiv ist nach zwei Merkmalen klassifiziert – Gesundheitszustand und Testergebnis. Beide Merkmale haben jeweils zwei Ausprägungen. Dies führt zu der folgenden Tabelle:
Angenommen, das Untersuchungskollektiv bestehe aus 10000 Personen. Dann ergibt sich für die im Beispiel beschriebenen Situationen die folgende absolute Verteilung:\(K\): Person ist krank \(\overline{K}\): Person ist gesund \(T\): Testergebnis ist positiv \(P(T\cap K) = 0.0192\) \(P(T\cap \overline{K})=0.0294\) \(P(T)=0.0486\) \(\overline{T}\): Testergebnis ist negativ \(P(\overline{T}\cdot K)=0.0008\) \(P(\overline{T}\cdot \overline{K})=0.9506\) \(P(\overline{T})=0.9514\) \(P(K)=0.02\) \(P(\overline{K})=0.98\) \(P(\Omega)=1\)
\(K\) \(\overline{K}\) \(T\) 192 294 486 \(\overline{T}\) 8 9506 9514 200 9800 10000 - Aus einer gegebenen Vierfeldertafel lassen sich zwei verschiedene Baumdiagramme gewinnen – abhängig davon, ob \(\Omega\) zuerst nach dem einen Merkmal zerlegt wird oder zuerst nach dem anderen. Seien bspw. die Zerlegungen von \(\Omega\) einerseits männlich (M) und weiblich (W) und andererseits krank (K) und gesund (\(\overline{K}\)). Dann ergeben sich die beiden folgenden Baumdiagramme, deren Pfade sich jeweils im entsprechenden Feld der Vierfeldertafel „treffen“:

- Im Baumdiagramm lassen sich die bedingten Wahrscheinlichkeiten unmittelbar ablesen. In der Vierfeldertafel hingegen müssen sie aus deren Daten erst berechnet werden.
- Die Stufung im Baumdiagramm legt eine Orientierung, bzw. Richtung in der Reihenfolge der Ereignisse fest. Dieser dynamische Charakter des Diagramms (im Gegensatz zum statischen Charakter der Vierfeldertafel) kann die Lösung einer Aufgabe unter Umständen erschweren. Bspw. kann im linken obigen Diagramm die bedingte Wahrscheinlichkeit P(W|K) abgelesen werden, aber nicht die bedingte Wahrscheinlichkeit P(K|W).

1.6. Aufgaben

Aufgaben

Aufgabe 1
In einer Schachtel befinden sich 24 in schwarzer Folie eingewickelte Pralinen. 18 Pralinen haben einen Überzug aus Vollmilchschokolade und sechs einen aus weißer Schokolade. Zwei Drittel der Vollmilchschokoladen-Pralinen (V) haben eine Marzipanfüllung (M). Insgesamt gibt es 16 Pralinen mit Marzipanfüllung.
Formulieren Sie zum Ergebnis \(P_\overline{V}(M)=\frac{4}{6}\) eine geeignete Aufgabenstellung und erläutern Sie diese durch ein begründetes Vorgehen.

Aufgabe 2
Zeigen Sie: Besitzen die unvereinbaren Ereignisse A und B je positive Wahrscheinlichkeiten, dann sind diese Ereignisse nicht stochastisch unabhängig.

Aufgabe 3
Sei \((\Omega, \wp (\Omega), P )\) ein endlicher Wahrscheinlichkeitsraum. Zeigen Sie: Für beliebige Ereignisse A und B gilt: \[P(A)=P(A\cap B) + P(A\cap\overline{B})\]

Aufgabe 4
In einem Hotel gibt es 200 Einzelzimmer. Eine Zimmer-Reservierung wird mit einer Wahrscheinlichkeit von \(\frac{1}{5}\) annulliert. Wie viele Reservierungen kann eine Hotel-Managerin für einen Tag zulassen, sodass das Risiko einer Überbuchung höchstens 0,025 beträgt?

Aufgabe 5
Untersuchen Sie den Zusammenhang zwischen Unabhängigkeit und Unvereinbarkeit zweier Ereignisse A und B.

Aufgabe 6
Das Eintreten von A sei notwendig für das Eintreten von B. Was lässt sich über die Unabhängigkeit von A und B sagen?

Aufgabe 7
Drei Spieler/innen A, B und C werfen mit jeweils einem Würfel. Spielerin A gewinnt, wenn sie eine 1, 2 oder 3 wirft. Spielerin B gewinnt, wenn sie eine 4 oder 5 wirft. Spieler C gewinnt, wenn er eine 6 wirft. Spielerin A beginnt, gibt dann den Würfel an B weiter, die nach ihrem Wurf den Würfel an C weitergibt. Es wird so lange weiter gewürfelt, bis jemand zum ersten Mal gewinnt. Wie groß ist die Wahrscheinlichkeit, dass Spieler C das Spiel gewinnt?

Aufgabe 8
Beweisen Sie die folgenden Aussagen:
Sind die Ereignisse \(A\) und \(B\) stochastisch unabhängig, dann gilt auch:
- \(\overline{A}\) und \(B\) sind unabhängig
- \(A\) und \(\overline{B}\) sind unabhängig
- \(\overline{A}\) und \(\overline{B}\) sind unabhängig

Aufgabe 9
Wie groß ist die Wahrscheinlichkeit, dass fünf, in einer Großstadt zufällig ausgewählte, Personen an verschiedenen Wochentagen Geburtstag haben?

Aufgabe 10
Bei einem Zufallsexperiment werden zwei verschiedene Laplace-Würfel geworfen und die Augensumme berechnet.
- Geben Sie einen geeigneten Wahrscheinlichkeitsraum \(\Omega\) für dieses Experiment an.
-
Welches der folgenden Ereignisse hat die größere Wahrscheinlichkeit?
A: Die Augensumme ist gerade.
B: Die Augensumme ist größer als 7.

Aufgabe 11
In einer Gärtnerei werden Samenkörner verwendet, die mit einer Wahrscheinlichkeit von 95% keimen. Wie groß ist die Wahrscheinlichkeit, dass von sieben ausgesäten Körnern
- genau drei Körner keimen?
- mehr als die Hälfte keimen?

Aufgabe 12
Eine Studentin hat in einer Klausur eine Multiple-Choice-Aufgabe mit n möglichen Antworten zu lösen, von denen genau eine richtig ist. Hat sich die Studentin gründlich auf die Klausur vorbereitet (dafür sei die Wahrscheinlichkeit 0,8), dann kann sie die Frage richtig beantworten. Andernfalls wählt sie eine der n Antworten willkürlich aus.
- Wie groß ist die Wahrscheinlichkeit (in Abhängigkeit von n), dass die Studentin sich auf die Prüfung gründlich vorbereitet hat, wenn sie die Frage richtig beantwortet hat?
- Wie groß muss n sein, damit die unter a) berechnete Wahrscheinlichkeit größer oder gleich 0,95 ist?

2. Zentrale Sätze der Stochastik
In diesem Modul werden zwei zentrale Sätze, bzw. Sachverhalte der Wahrscheinlichkeitsrechnung vorgestellt, die insbesondere eine wichtige Grundlage der schließenden Statistik darstellen.
2.1. Die Tschebyscheff-Ungleichung und das schwache Gesetz der großen Zahlen


Ausgangspunkt: Erwartungswert und Varianz
Die Kennwerte Erwartungswert und Varianz einer Zufallsvariablen lassen Rückschlüsse auf deren zugrunde liegende Verteilung zu, auch wenn diese nicht bekannt ist.
Dabei stellt die Varianz ein Maß für die Streuung der Werte, die \(X\) annimmt, um den Erwartungswert \(E(X)\) dar. Sie ermöglicht es, Schranken für die Wahrscheinlichkeit zu berechnen, dass ein Wert der Zufallsvariable \(X\) von ihrem Erwartungswert \(E(X)\) abweicht (bzw., wie groß diese Abweichung ist).
So lässt sich bspw. zu einer positiven Zahl \(a\) fragen, mit welcher Wahrscheinlichkeit die Zufallsvariable \(X\) um weniger als \(a\) von ihrem Erwartungswert abweicht, dass also gilt \(E(X)-a < X < E(X)+a\), bzw. \(|X-E(X)| < a\)
Die Werte von \(X\) liegen also innerhalb des folgenden Intervalls \(A\):
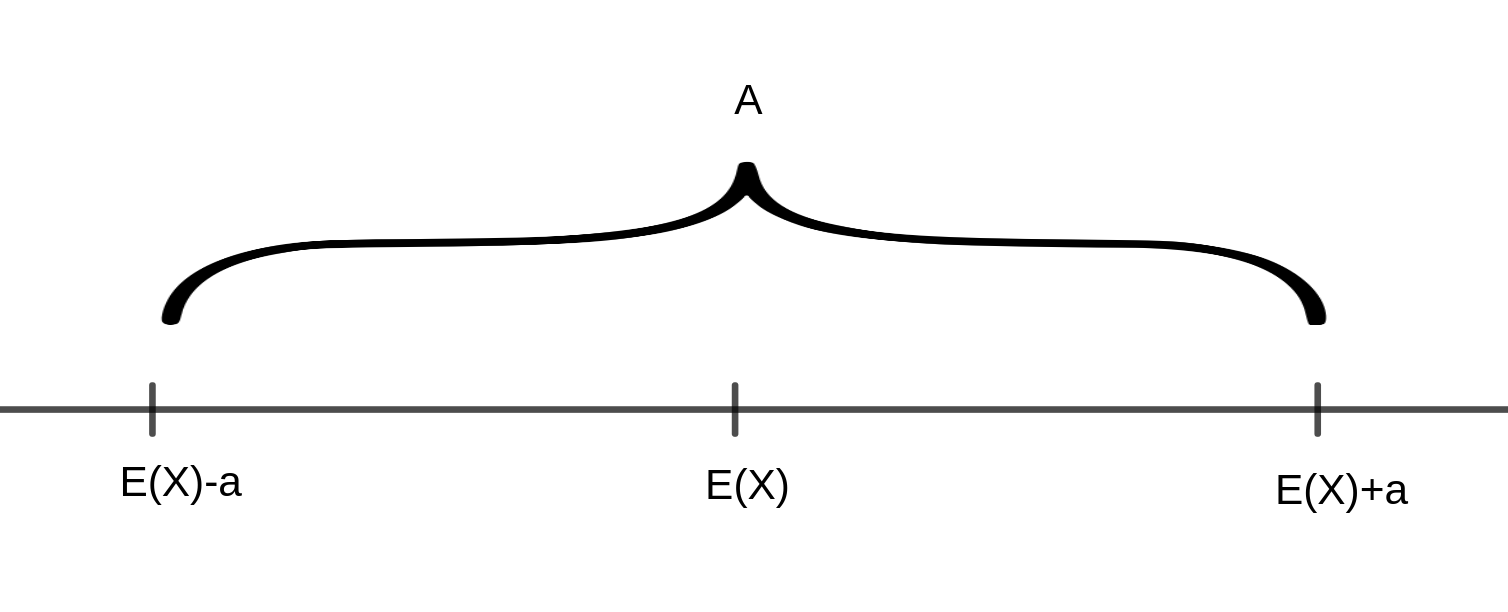
Die Gegenwahrscheinlichkeit gibt an, mit welcher Wahrscheinlichkeit die Werte von \(X\) außerhalb dieses Intervalls liegen, also \(|X-E(X)|\geq a\)
Letztere lässt sich mit Hilfe der Ungleichung von Tschebyscheff abschätzen:

Satz (Ungleichung von Tschebyscheff)
Sei \(X\) eine diskrete Zufallsvariable mit dem Erwartungswert \(E(X)=\mu\) und der Varianz \(V(X)=\sigma ^2\). Dann gilt für jede Zahl \(a>0\)
\[P(|X-E(X)|\geq a)\leq \frac{V(X)}{a^2}\]
Unter Verwendung des Gegenereignisses erhält man die folgende – gleichwertige – Formulierung:
\[P(|X-E(X)|< a )\geq 1-\frac{V(X)}{a^2}\]
Anmerkungen:
- Die Ungleichung von Tschebyscheff gilt nicht nur für diskrete, sondern auch für abstrakte Zufallsvariablen.
- Die Ungleichung ist nur dann nützlich, wenn \(\sigma =\sqrt{(V(X))} < a\) ist. Andernfalls erhält man lediglich die triviale Aussage, dass die Wahrscheinlichkeit \(\leq 1\) ist bzw. \(\leq t\) für eine Zahl \(t>1\).
- Die Ungleichung gilt für beliebige Zufallsvariablen und ist daher in ihrer Allgemeingültigkeit von theoretischem Nutzen. Für spezielle Verteilungen gibt es allerdings bessere Abschätzungen.
Aus der Ungleichung von Tschebyscheff lassen sich Folgerungen über die Lage der „Wahrscheinlichkeitsmasse“ ableiten:
Setzt man für a ein ganzzahliges Vielfaches \(k\cdot\sigma\) der Standardabweichung \(\sigma =\sqrt{V(X)}\) ein, so ergibt sich:
\[P(|X-E(X)|\geq k\sigma )\leq\frac{1}{k^2}\]
bzw.
\[P(|X-E(X)|< k\sigma )\geq 1-\frac{1}{k^2}\]
Für \(k=2\) ergibt sich bspw.
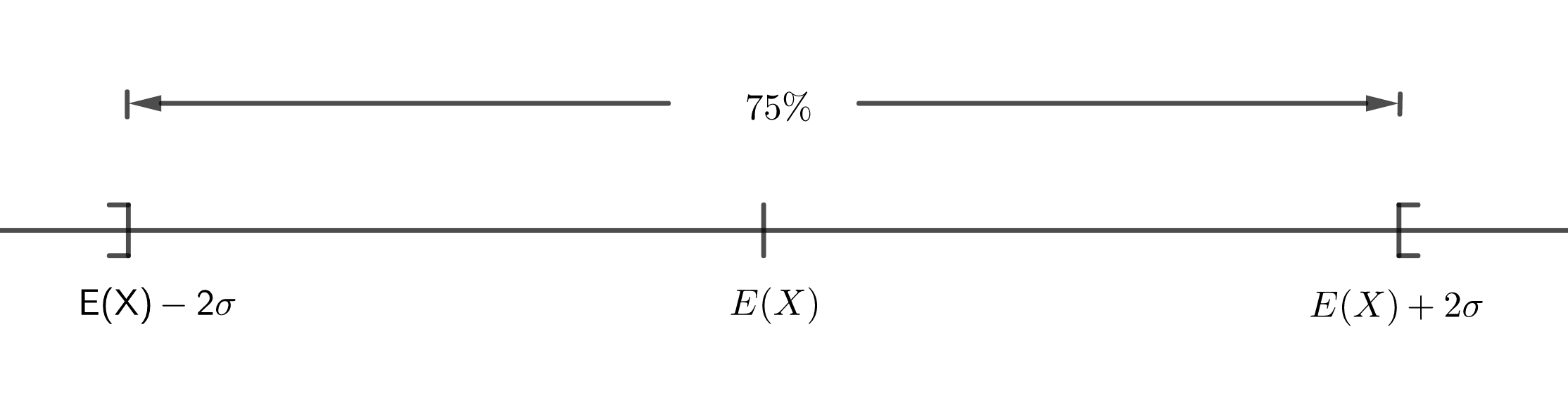
\[P(|X-E(X)|< 2\sigma )\geq \frac{3}{4}\]
Dies bedeutet, dass die Wahrscheinlichkeit, dass \(X\) Werte annimmt, die sich um weniger als zwei Standardabweichungen vom Erwartungswert \(E(X)\) unterscheiden, bei mehr als 75% liegt. D.h., dass mindestens 75% der vorhandenen „Wahrscheinlichkeitsmasse“ (von der Größe 1) auf das Intervall \(]E(X)-2\sigma ,E(X)+2\sigma [\) entfallen:

Beispiel - Ziehen mit Zurücklegen
Eine Urne enthalte 12 rote und 8 blaue Kugeln. Nacheinander werden 5 Kugeln mit Zurücklegen gezogen. Dabei soll die Zufallsvariable \(X\) die Anzahl der gezogenen roten Kugeln beschreiben.
- Wie groß ist der Erwartungswert \(E(X)\) der Zufallsvariablen?
Es wird eine Binomialverteilung zugrunde gelegt. \[E(X)=n\cdot p\text{ mit }n=5\text{ und }p=\frac{12}{20}=\frac{3}{5}\] Also ergibt sich \(E(X)=3\). - Berechnen Sie mit Hilfe der Tschebyscheff’schen Ungleichung \(P(|X-3|\geq 1)\).
Zunächst wird die Varianz \(V(X)\) berechnet: \[V(X)=n\cdot p\cdot (1-p)=5\cdot\frac{3}{5}\cdot\frac{2}{5}=\frac{6}{5}=1.2\] Mit der Ungleichung von Tschebyscheff folgt dann: \[P(|X-3|\geq 1)\leq \frac{1.2}{1^2}=1.2 \] Da für jede Wahrscheinlichkeit \(P\) gilt, dass \(P\leq 1\), ist diese Aussage trivial. Eine präzise Berechnung erfolgt unter 3). - Berechnen Sie P(|X-3|≥1) „exakt“ für die vorliegende Verteilung.
Es gilt: \[P(|X-3|\geq 1)=1-P(|X-3|< 1)\] \(X\) nimmt die Werte 0,1,2,3,4,5 an. \(|X-3|< 1\) gilt dabei nur für \(X=3\). \[P(X=3)={5\choose 3}\cdot {3\choose 5}^\cdot{2\choose 5}^2=10\cdot \frac{27}{125}\cdot \frac{4}{25}\approx 0.3456\] Damit gilt: \[P(|X-3|\geq 1)=1-0.3456=0.6544\approx 0.65\]

Schwaches Gesetz großer Zahlen
Das schwache Gesetz großer Zahlen (SGGZ) nach Jakob Bernoulli stellt die Verbindung her zwischen dem formalen Wahrscheinlichkeitsbegriff und
- der in der Realität zu beobachtenden Stabilität relativer Häufigkeiten
- der Verwendung der relativen Häufigkeit eines Ereignisses als Schätzwert für dessen Wahrscheinlichkeit.
Analog zu Kütting (1999) beschränkt sich dieser Kurs im Hinblick auf das SGGZ auf die Betrachtung von relativen Häufigkeiten in Bernoulli-Ketten der Länge \(n\).

Satz (Schwaches Gesetz großer Zahlen)
Es sei \(A\) ein Ereignis, das bei einem Zufallsexperiment mit der Wahrscheinlichkeit \(P(A)=p\) eintrete. Die relative Häufigkeit des Ereignisses \(A\) bei \(n\) unabhängigen Wiederholungen des Zufallsexperiments sei mit \(h_n\) (Bernoulli-Kette der Länge \(n\)) bezeichnet. Dann gilt für jede positive Zahl \(\epsilon\):
\[\lim_{n\to\infty} P(|h_n-p|<\epsilon)=1\]
bzw. (gleichwertig)
\[\lim_{n\to\infty} P(|h_n-p|\geq\epsilon)=0\]
(Zum Beweis wird auf Kütting, 1999 verwiesen. Eine allgemeinere Version des schwachen Gesetzes der großen Zahlen findet sich z.B. bei Henze, 2018.)
Umgangssprachlich formuliert: Wächst \(n\) über alle Grenzen, dann strebt die Wahrscheinlichkeit, dass die relative Häufigkeit des Ereignisses \(A\) um weniger als eine beliebig kleine vorgegebene Zahl \(\epsilon\) von der tatsächlichen Wahrscheinlichkeit \(P(A)=p\) des Ereignisses \(A\) abweicht, gegen 1.
