Demokurs: Grundlagen der anwendungsbezogenen Hochschulmathematik: Aufgaben

1. Funktionen

1.5. Aufgaben

Aufgaben

Aufgaben zum 2. Kapitel "Funktionen"

Aufgabe 1: Parabeln I

Die Graphen der Funktionen

$f$ ,

$g$ mit

$f(x) = ax^2+ bx + c$ und

$g(x) = d(x-e)^2+ h$ sollen dieselbe Parabel darstellen. Welche Beziehung besteht zwischen den Variablen

$a$ ,

$b$ ,

$c$ ,

$d$ ,

$e$ und

$h$ ?

Aufgabe 2: Parabeln II

Wir betrachten die Parabeln

$P_b$ mit der Gleichung

$f(x) = 2x^2+ bx + 1$ ,

$b \in \mathbb{R}$ .

Bestimmen Sie den Scheitelpunkt $S_b$ der Parabeln $P_b$ (also in Abhängigkeit von $b$ ).
Zeichnen Sie – etwa mit Hilfe des Programms GeoGebra (kostenlos downloadbar unter http://www.geogebra.at) – die Ortslinie $OS_b$ , auf der sich der Scheitelpunkt von $P_b$ bewegt, wenn $b$ variiert wird. In die Lösung der Aufgabe soll ein Screenshot dieser Aufgabe eingebunden werden.
Bestimmen Sie die Gleichung für die Ortslinie $OS$ .

Aufgabe 3: Exponentialfunktion

Vergleichen Sie die beiden Funktionen mit $y = a \cdot 2^x$ und $y = 2^{(x+d)}$ für verschiedene Werte $a,d \in \mathbb{R}$ . Für welche $a$ bzw. $d$ -Werte stimmen die Graphen der beiden Funktionen überein?
Die allgemeine Exponentialfunktion lässt sich mit der Gleichung $f(x) = a \cdot b^{cx+d}$ mit $a,c,d \in \mathbb{R}; b \in \mathbb{R}^+$ beschreiben. Diese Gleichung ist äquivalent zu einer Gleichung mit nur drei Parametern $A,B,C$ , wobei $A,B,C \in \mathbb{R}$ bzw. $\mathbb{R}^+$ . Geben Sie den Zusammenhang zwischen $A,B$ und $C$ sowie $a,b,c$ und $d$ an!

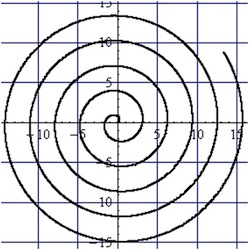
Aufgabe 4: Spirale

Zeichnen Sie die Kurve

$K(t) = (t \cdot \cos(t), t \cdot \sin(t))$ für

$0 < t < 20$ . Die Kurve lässt sich aus einer Bewegung entstanden denken und dynamisch interpretieren, indem

$t$ als Zeit verstanden wird. Man nennt diese Kurve Spirale.

Beschreiben Sie diese Bewegung!
Geben Sie die Gleichung abgebildeten Spirale an!

Aufgabe 5: Ellipse

Gegeben ist eine Ellipse

$E(x,y): \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ ;

$a,b \in \mathbb{R}^+$ . Geben Sie die Gleichung der Tangente an die Ellipse im Ellipsenpunkt

$P(x_0,y_0)$ an.

Hinweis: Gehen Sie vom Kreis

$K_a: x^2+ y^2= a^2$ aus und erzeugen Sie

$E$ durch eine Streckung bzw. Stauchung von

$K_a$ mit dem Faktor

$\frac{b}{a}$ parallel zur y-Achse. Gehen Sie dann von einer Kreistangente aus.

Aufgabe 6: Das Herz

Es gibt verschiedene Möglichkeiten, ein Herz mit Hilfe von mathematischen Funktionen zu zeichnen. Insbesondere kann ein Herz sehr unterschiedliche Formen besitzen. Zeichnen Sie aus Funktionsstücken (mit GeoGebra) ein Herz. Das Bild rechts zeigt eine Möglichkeit der Umsetzung.

Aufgabe 7: Funktion zweier Veränderlicher

Beschreiben Sie den Graphen $G$ der Funktion mit $f(x,y) = x^2+ y^2$ , indem Sie $G$ mit ausgewählten Ebenen schneiden und die Schittfiguren beschreiben.
Wir betrachten die beiden Ebenen im Raum mit $f(x,y) = 4x + y + 3$ und $g(x,y) = -x + 3y - 5$ in einem gemeinsamen Koordinatensystem. Zeigen Sie, dass die beiden Ebenen zueinander senkrecht sind.