Demokurs: Grundlagen der anwendungsbezogenen Hochschulmathematik: Exponentialfunktion und Wachstum

1. Funktionen

1.3. Exponentialfunktion und Wachstum

Exponentialfunktion und Wachstum

Exponential- und Wachstumsfunktionen

In diesem Kapitel lernen wir eine besonders wichtige Funktion kennen - die Exponentialfunktion. Danach werden wir das Wachstum beliebiger Funktionen an Hand des Wachstums bereits bekannter Funktionen kategorisieren.

Einführendes Beispiel: Lineares und exponentielles Wachstum

Beispiel 1:

Kapitalentwicklung bei einfacher Verzinsung

Bei einer einfachen Verzinsung werden in jedem Jahr nur die einfachen Zinsen in der Höhe von

$K_0 \cdot \frac{p}{100}$ zum Anfangskapital

$K_0$ hinzugerechenet. Die Zinsen der weiteren Jahre werden immer nur vom Anfangskapital

$K_0$ berechnet. Es wird also davon ausgegangen, dass die jährlichen Zinsen an den Anleger ausbezahlt werden. Es ergibt sich für das Kapital nach

$n$ Jahren

$K(n) = K_0 + K_0 \cdot \frac{p}{100} \cdot n$

Kapitalentwicklung mit Zinseszins

Bei einer Verzinsung mit Zinseszinsen werden jedes Jahr die Zinsen der vorangegangenen Jahre wiederum verzinst, d.h. das Anfangskapital

$K_0$ wird im jedem Jahr mit

$(1 + \frac{p}{100})$ multipliziert. Es ergibt sich für das Kapital nach

$n$ Jahren

$K(n) = K_0 \cdot (1 + \frac{p}{100})^n$

Aufgabe:
Erläutern Sie das Zustandekommen dieser Formel.

Die beiden Formeln für die Zunahme des Kapitals sind eigentlich nur für volle Jahre

$(n \in \mathbb{N})$ anwendbar, da die Bank jährlich verzinst. Der Graph für das Kapital nach

$n$ Jahren ist deshalb ein diskreter Graph.

Näherungsweise kann man aber auch mit einem Exponenten

$x \in \mathbb{R}$ arbeiten, um das Kapital zu beliebigen Zeitpunkten (z.B.

$x = 1, 75$ Jahre) zu berechnen. Der Graph für das Kapital nach einer beliebigen Zeitspanne

$x$ besteht in diesem Fall aus einer stetigen Kurve. (Diese kontinuierliche Entwicklung kann in den Applets über das Kontrollkästchen ein- bzw. ausgeschaltet werden.)

Das Anwachsen eines Kapitals nach der Funktionsgleichung

$K(x) = K_0 \cdot (1 +\frac{p}{100})^x$ nennt man exponentielles Wachstum. Dieses Wachstum wird durch die Funktionsgleichung eines neuen Funktionstyp beschrieben. Bei dieser Art von Funktion steht die unabhängige Variable

$x$ im Exponenten und wird deshalb Exponentialfunktion genannt.

Die allgemeine Exponentialfunktion

Definition 1 (Exponentialfunktion zur Basis a)

Die Funktion

$f: \mathbb{R} \rightarrow \mathbb{R}, \, f(x) = a^x = \exp (x \cdot \log(a))\,$ für

$a \in \mathbb{R}^+$

heißt Exponentialfunktion zur Basis $a$ .

$a>0$ wird hier echt positiv gewählt, da für

$a<0$ bspw. Ausdrücke der Form

$a^{\frac{1}{2}}=\sqrt{a}$ in

$\mathbb{R}$ nicht lösbar sind.
Für

$a=0$ hingegen sind bspw. Ausdrücke der Form

$a^{-1}=\frac{1}{a}$ nicht definiert.

Satz 1 (Funktionalgleichung)

Für alle

$x,y \in \mathbb{R}$ gilt:

$a^{(x+y)} = a^x \cdot a^y$

Beweis

Eigenschaften der allgemeinen Exponentialfunktion $x \rightarrow a^x$

Die Exponentialfunktion ist für alle $x \in \mathbb{R}$ definiert.
Sie nimmt nur positive Funktionswerte an.
Die Graphen aller Exponentialfunktionen der Form $f(x) = a^x$ gehen durch den Punkt $(0|1)$ .
Für $0 < a < 1$ ist $f(x)$ monoton fallend, für $a = 1$ konstant und für $a > 1$ monoton steigend.
Die Graphen von $f(x) = a^x$ und $g(x) = a^{-x}=\frac{1}{a^x}$ liegen symmetrisch bezüglich der y-Achse. Für beide Graphen ist die x-Achse horizontale Asymptote.
Für $0 < a < 1$ ist $f(x) = a^x$ monoton fallend, $f$ divergiert für $x \rightarrow -\infty$ und konvergiert gegen $0$ für $x \rightarrow \infty$
Für $a=1$ ist $f$ konstant
Für $a > 1$ ist $f(x) = a^x$ monoton steigend, $f$ divergiert für $x \rightarrow \infty$ und konvergiert gegen $0$ für $x \rightarrow -\infty$

Es gilt:

$a^0=1$ für alle

$a$
Es gilt:

$1^x=1$ für alle

$x$

$f(-x) = a^{-x} = g(x)$

$f(x) = a^{x} = a^{-(-x)} = g(-x)$

Aufgabe: Bearbeiten Sie folgende Aufträge im untenstehenden Applet.

(Diskussion von $x \rightarrow a^x$ ) Stellen Sie zunächst für $m$ und $b$ den Wert $1$ , für $c$ und $d$ den Wert $0$ ein und ändern Sie mit Hilfe des Schiebereglers den Wert der Basis $a$ und beschreiben Sie den Verlauf des Schaubildes für verschiedene Werte von $a$ . Verifizieren Sie die oben genannten Eigenschaften der Funktion $x \rightarrow a^x$ .
Warum existiert die Funktion $f(x)$ nicht für negative $a$ ?
(Diskussion von $x \rightarrow m \cdot a^x$ ) Lassen Sie wiederum $a$ fest (nicht $0$ ) und veränderen Sie nur $m$ . Beschreiben Sie die Auswirkungen auf das Schaubild und finden Sie eine bestimmte Eigenschaft für bestimmte Wertepaare von $m$ heraus.
(Diskussion von $x \rightarrow a^{b \cdot x}$ ) Lassen Sie nun $a$ fest (nicht $0$ ) und verändern Sie nur $b$ . Beschreiben Sie die Auswirkungen auf das Schaubild und finden Sie eine bestimmte Eigenschaft für bestimmte Wertepaare von $b$ heraus.
(Diskussion von $x \rightarrow a^x+ c$ ) Stellen Sie für $m$ und $b$ wieder den Wert $1$ und für $d$ den Wert $0$ ein und ändern Sie mit Hilfe des Schiebereglers den Wert von $c$ . Beschreiben Sie die Auswirkungen auf das Schaubild.
(Diskussion von $x \rightarrow a^{x+d}$ ) Stellen Sie für $m$ und $b$ wieder den Wert $1$ und für $c$ den Wert $0$ ein und ändern Sie mit Hilfe des Schiebereglers den Wert von $d$ . Beschreiben Sie die Auswirkungen auf das Schaubild.

Nebenbemerkung (freiwillig):
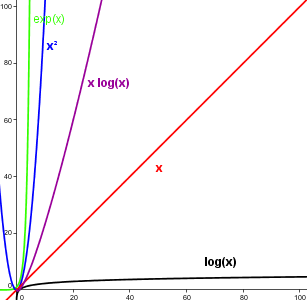
Beispiel 2 (Die Exponentialfunktion wächst schneller als jede Potenz von x):

Für beliebiges

$m \in \mathbb{N}$ gilt

$x^m < o(\exp(x))$ , denn für

$x > 0$ ist

$\exp(x) = \sum_{n=0}^\infty {\frac{x^n}{n!}} > \frac{x^{m+1}}{(m+1)!}$

und damit

$0 \ge \lim_{x \to \infty} \frac{x^m}{\exp(x)} \ge \lim_{x \to \infty} \frac{x^m}{\frac{x^{m+1}}{(m+1)!}} = 0$

Der Logarithmus - die Umkehrfunktion der Exponentialfunktion

Die Umkehrfunktion der Exponentialfunktion ist der Logarithmus

$\log_a(x) : \mathbb{R}^+ \rightarrow \mathbb{R}$ . Er ist stetig und streng monoton wachsend.

Die Logarithmus-Funktion ergibt sich als Umkehrfunktion durch Umformen der Exponentialfunktion:

$y=f(x)=a^x$

Dann ist:

$x=f^{-1}(y)=log_a(y)$

Um die Funktion im gewohnten Koordinatensystem darzustellen, wird sie allerdings ebenfalls in der Form $x \rightarrow f^{-1}(x)$ verwendet.

Aufgabe: Bearbeiten Sie folgende Aufträge im untenstehenden Applet.

Ändern Sie mit Hilfe des Schiebereglers den Wert von $a$ und beschreiben Sie den Verlauf des Schaubildes für verschiedene Werte von $a$ . Was haben alle Funktionen gemeinsam? Welche Unterschiede für welche $a$ gibt es?
Was fällt Ihnen im Vergleich von Exponentialfunktion und Logarithmusfunktion auf? Beschreiben Sie die Lage beider Schaubilder zueinander.

Satz 2 (Funktionalgleichung)

Für alle

$x, y \in \mathbb{R}^+$ gilt:

$\log_a(x \cdot y) = \log_a(x) + \log_a(y)$

Beweis