Lecture - Image Processing
3. Basic Methods II: Image operations
3.8. Negative Transfer Function
This basic example of a transfer function simply assigns every pixel their negative value. Areas of high intensity become dark and vice versa. Since pixel values run on a certain range (0-255 in our case) the "mirroring" of their value is being performed according to their maximum value:
\( f(q) = p_{max} - p \)
Everyone who has used an analog camera at some point knows that exposing a photographic film to the light creates a negative. Not so long ago astronomers used large photographic plates, which worked in the same way. An advantage of using negatives in astronomy is that faint details are more visible to the eye compared to the positive. Differences between two light shades is easier to spot than for two dark shades.
For this and the following examples of applicable transfer functions we are going to use the black and white picture of the Horsehead Nebula, pictured below. It's wide range and non-uniform distribution of brightness demonstrates very well the capabilities of the different functions.

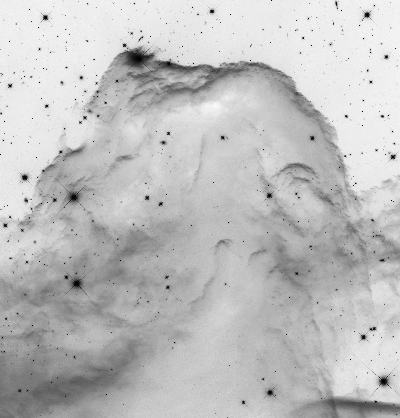
Fig. 3.9: Black and white image (left) and negative (right) of the Horsehead Nebula, Image Credit: NASA, ESA & Hubble Heritage Team (AURA/STScI)
