Lecture - Image Processing
3. Basic Methods II: Image operations
3.4. Geometric Operations - Scaling
Changing the size of an image is also called scaling. This may be done for increasing or decreasing size, respectively. Assuming an equal image scaling of both axes the process can be expressed in its most basic form via:
\( x' = s \, x \)
\( y' = s \, y \)
with the scale factor \( s \). The coordinate of every point is multiplied with the same factor.To scale points relative to a coordinate set \( (x_0, y_0) \), which may be for example \( (0, 0) \) or the middle of the image, the equations become:
\( x' = x_0 + s(x - x_0) \)
\( y' = y_0 + s(y - y_0) \) .
Again, for computing the new and scaled image we must use the equations that are solved for \( x \) and \( y \) in order to obtain all contributions of surrounding pixels in the old image that is mapped onto a new grid. Scaling an image up with an integer factor always results in the best image quality since no interpolation is necessary. Non-integer transformations require interpolation and result in a slightly smoothed image. The figure below shows on the right hand side an example of scaling the factor 2 and the point \( (x_0,y_0) \) in the top left corner of the image. The left hand side shows the scaling up with a factor close to 1. This results in visible image artifacts that come from the interpolation of four pixels of the old image in most cases whereas some pixel values are taken entirely from the old image. In the example below, the scaling also results in a smoothed out edge on two sides.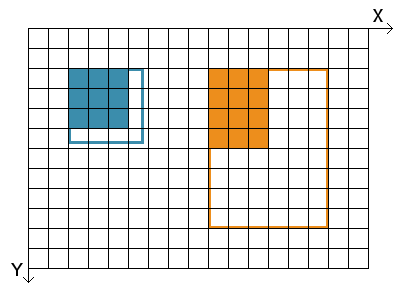
Fig. 3.3: Scaling of an Image. Left: scale factor close to 1, Right: scale factor 2.
