Lecture - Image Processing

The most simple geometric transform is the translation along one of the image axis or all at once. An image, or the ensemble of pixels that are translated in the coordinate system, undergo the equations:

\( x' = x + x_T \) 

\( y' = y + y_T \)

where \( x' \) and \( y' \) are the coordinates of a pixel \( P \) in the new image and \( x \) and \( y \) the coordinates of the original. The distance of which \( P \) is translated in every direction is denoted by \( x_T \) and \( y_T \), respectively. Figure 3.1 shows two examples of a translation in both directions. Usually, the order in which both translations are performed is arbitrary. In reality the boundary conditions of the image or coordinate system need to be taken into account in every step. One translation may easily shift pixels over the edge of the coordinate system, leading to a loss of information. 

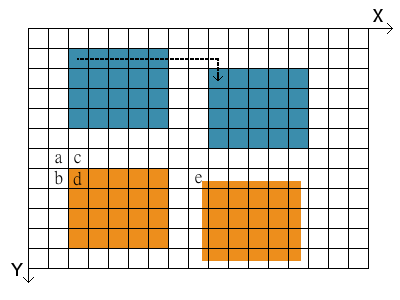
Fig. 3.1:  Translation of image by an integer number of pixels (blue images), and non-integer number (orange images).

The translation of an image with an integer number of pixels is not always this case however. What if the translation in Fig. 3.1 is not 8 pixels to the right and 1 pixel down, but for example 7.52 right and 0.74 down? A new pixel value needs to be calculated, where the new one would be (but can't be since the coordinate system does not allow it). In order to do that we need to perform an interpolation of the pixel value. In doing this, we calculate the weighted average of the four pixels that are surrounding the point in the old image. This new value is then assigned to the new pixel in the translated image.

The weighting of all surrounding pixels in the old image (pixels named a, b, c, and d in Fig. 3.1) is done by using the fractional contribution of each pixel, measured by the distance to the point. Have a look at the new image that is transferred by non-integer numbers (orange). One of the former pixels without value (white) now has a bit of orange in it (pixel named e). Consequently, we need to calculate the weighted mean for this pixel, which will become only a bit orange. The new image gets blurred out at the edges as a result of the non-integer translation.

If we want to write a program that translates an old image into a new one by applying a certain instruction, we need to work "backwards". The equations for the translation need to be set up so that the new image can be constructed by referring to pixels of the old image. The translation of an image into a new one is done pixel by pixel. If more than one pixel is needed for the calculation of the value of a new pixel in the new image, like interpolation, it is much more advantageous to start with a new pixel and refer to one or more old pixels.

The procedure of interpolation is necessary whenever the grid of the new pixels does not exactly match the old grid. Besides non-integer pixel translation this will occur in similar applications, i.e. rotation, scaling, and resampling.