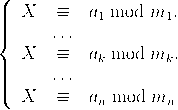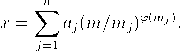3. Modul: Teilbarkeit ganzer Zahlen und modulare Arithmetik

______________________________________________________________________________

vhb - Kurs: Grundlagen der elementaren Zahlentheorie

III.5. Rechnen mit Restklassen

__________________________________________________________________________

Eine zahlentheoretische Besonderheit bildet das Rechnen mit sogenannten Restklassen. Eine besonders spannende Anwendung hierfür ist beispielsweise das Verschlüsselungsverfahren RSA.

Zunächst soll das Rechnen mit Restklassen eingeführt werden. Sei hierzu m eine natürliche Zahl, so definiert

a ∼ b : ⇔ m | (a − b)

eine Äquivalenzrelation auf ℤ. Wir prüfen dies nach: Zunächst gilt m∣0 = a−a für beliebiges a ∈ ℤ, womit die Reflexivität folgt: a ∼ a. Für den Nachweis der Symmetrie a ∼ b⇔b ∼ a bemerken wir, dass jeder Teiler von b − a auch ein Teiler von a − b ist. Ferner folgt im Falle m∣(b − a) und m∣(c − b) auch

m | (c − b + (b − a)) = c − a,

also die Transitivität. Damit ist der Nachweis der Äquivalenzrelationseigenschaft erbracht. Statt a ∼ b schreiben wir suggestiver

a ≡ b mod m : ⇔ m | (a − b)

und sagen a ist kongruent b modulo m; hierbei heißt m der Modul und a ≡ b mod m nennt man eine Kongruenz. Wir schreiben a≢b mod m und sagen a ist inkongruent b modulo m, wenn m ∤ (b − a).

Kongruenzen sind eine Verallgemeinerung von Gleichungen, denn mit a = b gilt sicherlich auch a ≡ b mod m für jedes beliebige m ∈ ℕ. Insbesondere bestehen folgende Rechenregeln: Für beliebige a,b,c,d ∈ ℤ und m ∈ ℕ gelten

a ≡ a mod m,
a ≡ b mod m⇔b ≡ a mod m,,
a ≡ b,b ≡ c mod m ⇒ a ≡ c mod m,
a ≡ b,c ≡ d mod m ⇒ ax + cy ≡ bx + dy mod m,
a ≡ b,c ≡ d mod m ⇒ ax ⋅ cy ≡ bx ⋅ dy mod m,
ac ≡ bc mod m ⇒ a ≡ b mod (m∕ggT(m,c)),
a ≡ b mod m ⇒ aⁿ≡ bⁿ mod m für jedes n ∈ ℕ.

Die ersten drei Rechenregeln reflektieren, dass es sich bei der Kongruenz um eine Äquivalenzrelation handelt (s.o.). Von den restlichen Rechenregeln beweisen wir hier nur die 6. Rechenregel: Nach Voraussetzung gilt m∣(a − b)c und weil ggT(m,c) sowohl m als auch c teilt, folgt

(m ∕ggT (m, c)) ⋅ ggT(m, c) | (a − b) ⋅ (c∕ggT (m, c)) ⋅ ggT (m, c)

und mit der Teilerfremdheit von m∕ggT(m,c) und c∕ggT(m,c) ergibt sich (6.).
Wir schreiben die Äquivalenzklassen bzgl. ∼ als

a mod m := {b ∈ ℤ : a ≡ b mod m } = {b = a + mk : k ∈ ℤ} =: a + m ℤ

und sprechen von der Restklasse a modulo m. Eine Restklasse besteht dann aus allen ganzen Zahlen, die denselben Rest bei Division durch m lassen. Statt a könnte natürlich auch jedes andere Element b ∈ a mod m als Repräsentant dieser Restklasse herhalten, also etwa

... = − 2 mod 3 = 1 mod 3 = 4 mod 3 = 7 mod 3 = ...

Als Nächstes wollen wir Restklassen addieren und multiplizieren. Es stellt sich dabei heraus, dass man mit Restklassen zu einem fest fixierten Modul wie mit Zahlen rechnen kann! (Dies rechtfertigt gewissermaßen auch, dass wir oft a statt a mod m schreiben.) Hierzu definieren wir die Addition vermöge

(a mod m) + (b mod m) := (a + b) mod m

sowie die Multiplikation durch

(a mod m ) ⋅ (b mod m ) := (a ⋅ b) mod m.

Diese Verknüpfungen sind wohldefiniert, hängen also nicht vom gewählten Repräsentanten ab, wie wir am Beispiel der Addition illustrieren:
Mit a ≡ A und b ≡ B mod m existieren per Definition ganze Zahlen k,ℓ mit a = A + km und b = B + ℓm, so dass

(a mod m) + (b mod m) = (a + b) mod m

= (A + B + (k + ℓ)m) mod m

= (A + B) mod m = (A mod m) + (B mod m).

Nun betrachten wir sämtliche Restklassen eines festen Moduls gemeinsam. Modulo m bilden die Restklassen

0 mod m, 1 mod m, ..., m − 1 mod m

ein vollständiges Restsystem modulo m. Dieser Name ist gerechtfertigt, denn mit a mod m = b mod m folgt unmittelbar m∣(b − a), was für a,b ∈ {0, 1,…,m − 1} nur mit a = b möglich ist; ferner lässt sich jede Restklasse b mod m mit einem b ∉ {0, 1,…,m − 1} mittels Divison mit Rest als eine der obigen Restklassen a mod m mit einem a ∈ {0, 1,…,m − 1} nachweisen. Es gibt also genau m verschiedene Restklasse modulo m. Wir notieren die Menge der Restklassen modulo m mit

ℤ∕m ℤ := {0 mod m, 1 mod m, ..., m − 1 mod m }.

Hierbei handelt es sich also um eine Menge, deren Elemente wiederum Mengen sind, genauer: um eine endliche Menge, deren Elemente jeweils unendliche Mengen sind. Anhand von ausgewählten Beispielen kann man erkennen, dass solche Mengen die aus Kapitel II bekannten Axiome von Gruppen, Ringen oder sogar Körpern erfüllen.
Diese Strukturen sind kein Zufall

Satz.

Sei m eine natürliche Zahl, dann ist die Menge ℤ∕mℤ mit der oben definierten Addition und Multiplikation ein kommutativer Ring, der sogenannte Restklassenring modulo m.

Beweis. Die Menge ℤ∕mℤ ist mit der oben eingeführten Addition eine abelsche Gruppe mit neutralem Element 0 mod m bzgl. der Addition (was sich aus unseren bisherigen Überlegungen unmittelbar ergibt). Mit der oben definierten Multiplikation ist ℤ∕mℤ eine Halbgruppe und 1 mod m ist das neutrale Element der Multiplikation, insbesondere gelten die Distributiv- und Assoziativgesetze. Damit ist ℤ∕mℤ ein Ring und der Satz bewiesen. qed.

Die Idee der Restklassenbildung ist oft hilfreich, um redundante Information los zu werden, mit dem Vorteil von der unendlichen Menge ℤ zur endlichen Menge von Restklassen modulo m übergehen zu können. Die Restklassenarithmetik hat ganz verschiedene Anwendungen, wie beispielsweise bei ISBN-Nummern.

Eine Restklasse a mod m heißt prim, wenn a und m teilerfremd sind. Wegen ggT(a + km,m) = ggT(a,m) ist entweder jedes Element einer Restklasse oder keines teilerfremd zum Modul m. Die primen Restklassen modulo m = 8 sind damit

1, 3, 5, 7 mod 8.

Die Menge der primen Restklassen modulo m ist offensichtlich multiplikativ abgeschlossen (denn mit a und b ist auch das Produkt ab teilerfremd zu m). Die Anzahl φ(m) der primen Restklassen modm zählt die Eulersche φ-Funktion. Es gelten (wie man sich leicht überlegt)

φ(8) = 4, φ(10) = 4 und φ(2^k) = 2^k+1

bzw.

φ(p) = p-1 und φ(p^k) = p^k(1 - 1/p) für p prim.

Ein Vertretersystem der φ(m) vielen primen Restklassen modm heißt primes Restsystem modulo m. Ist b₁,…,b_φ(m)ein primes Restsystem modm, so auch ab₁,…,ab_φ(m), sofern a teilerfremd zu m ist. Es ist klar, dass mit einem zum Modul teilerfremden a mit b_j auch ab_j eine prime Restklasse modulo m ist. Aus ab_j≡ ab_k mod m folgt mit der 6. Rechenregel auch b_j≡ b_k mod m. Also sind mit b_j und b_k auch ab_j und ab_k inkongruente Restklassen modulo m. Diese Rechenregeln bilden die Grundlage weiterer wichtiger Sätze zum Restklassenkalkül, wie beispielsweise der Satz von Euler.
Die Idee der primen Restklassen (bzw. multiplikativ Inversen) hilft auch beim Lösen von linearen Kongruenzen.
Diese Idee lässt sich verallgemeinern

Satz.

Seien a,b ∈ ℤ und m ∈ ℕ. Dann ist die Kongruenz

aX ≡ b mod m

genau dann lösbar, wenn ggT(a,m)∣b. In diesem Fall gibt es genau ggT(a,m) inkongruente Lösungen modulo m.

Beweis. Nach dem Satz von Bézout ist die lineare diophantische Gleichung

aX = b + mY bzw. aX − mY = b

genau dann lösbar, wenn b ein Vielfaches von ggT(a,m) ist. In diesem Fall existieren also ganze Zahlen x und y, so dass

ax = b + my bzw. ax ≡ b mod m.

Damit ist eine lösende Restklasse modulo m also gefunden. Ist ggT(a,m) > 1, so ergeben sich mehrere Lösungen modulo m über die 6. Kürzungsregel.qed.

Der Beweis ist konstruktiv (dank des euklidischen Algorithmus versteckt im Satz von Bézout).
In einem alten chinesischen Mathematikbuch vor ca. zweitausend Jahrhen stellte sein Verfasser Sun-Tsu folgende Aufgabe:

Aufgabe 1.

Finde eine Zahl, welche Zahl bei Division durch 3 den Rest 2, bei Division durch 5 den Rest 3 und bei Division durch 7 den Rest 2 lässt.

Hierher rührt auch der Name des folgenden Resultates:

Satz (Chinesischer Restsatz).

Es seien m₁,…,m_n∈ ℕ paarweise teilerfremd und a₁,…,a_n ∈ ℤ beliebig. Dann besitzt das lineare Konruenzsystem

kongruenzen

eine eindeutige Lösung x mod m, wobei m := m₁⋅…⋅ m_n.

Eine interessante Interpretation des chinesischen Restsatzes ist die folgende: In einem hinreichend kleinen Intervall ist eine ganze Zahl also eindeutig durch ihre Reste modulo kleiner Primzahlen bestimmt!

Beweis. Wir haben die Existenz und die Eindeutigkeit dieser Lösung zu zeigen. Hierzu setzen wir

chin

Hierbei ist m∕m_j eine ganze Zahl (klar) mit m∕m_j≡ 0 mod m_k für k≠j; ansonsten, wenn also j = k, sind m∕m_j und m_j = m_k teilerfremd. Mit dem Satz von Euler folgt

Also gilt x ≡ a_k mod m_k für 1 ≤ k ≤ n und x ist eine Lösung unseres linearen Kongruenzsystems. Dies beweist also die Existenz einer Lösung; nun der Nachweis der Eindeutigkeit: Eine Restklasse y ist genau dann eine Lösung, wenn m_j∣(x − y) für 1 ≤ j ≤ n gilt. Mit der paarweisen Teilerfremdheit der m_j ist dies äquivalent zu m = m₁⋅…⋅m_n∣(x−y) bzw. x ≡ y mod m, was zu zeigen war. qed.