Hello everyone,
we have two question concerning exercise 6.2, or more generally the calculation of the sum over C(r).
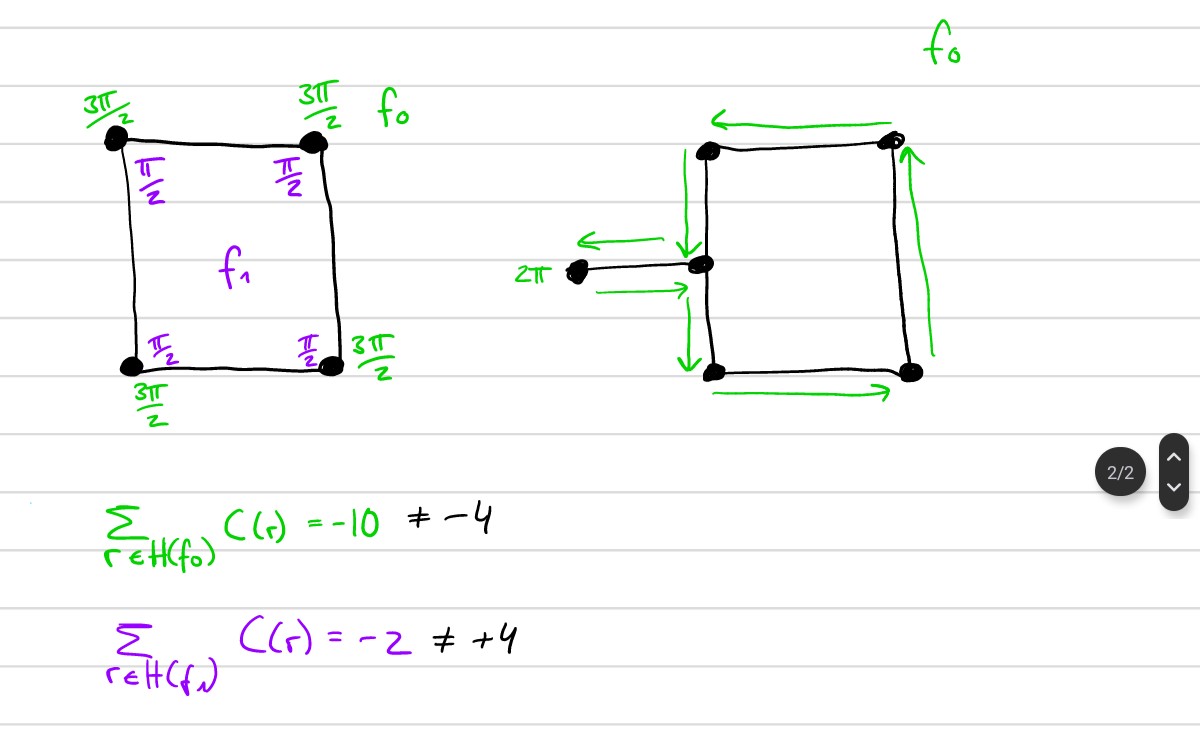
In the picture below, the left shows an example how we set the angles alpha and hence the values for the sums when considering the outer face f0 or the inner face f1. The values do not match the values (-4, +4) we would expect from the lecture. Maybe someone can help us and tell us what we did wrong.
On the right, we have a second question: In the script it is said that alpha can be 2pi. The only case we found, where that would be the case, is when we have a vertex with degree one. The question is if we imagined the waking through the edges correctly, or if this would oppose the calculations/algorithms in any way.