Demokurs: Approach to the Basics of Calculus - ENGLISH
Sequences - Basics

|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Definition 1 (Sequence). Let M be a non-empty set. A sequence is a function:
Occasionally we speak about a sequence in M .
Note: Characteristics of the set ℕ give certain characteristics to the sequence. Because ℕ is ordered, the terms of the sequence are ordered.
Definition 2 (Terms and Indices): A sequence is denoted ( a 1 , a 2 , a 3 , … ) or for short ( a n ) n instead of f ( n ) . The numbers a 1 ,a 2 ,a 3 , … ∈ M are called the terms of the sequence. Because of the mapping
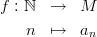
A few easy examples |
Random sequence of coloured squares. At any one time only one term of the sequence is displayed.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Example 1: The sequence of natural numbers 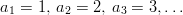 This special sequence has the property that every term is the same as its index. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
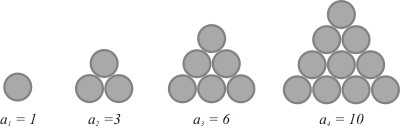
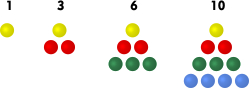
Example 2: The sequence of triangular numbers
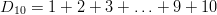
In general form the sequence is defined as: D n = 1 + 2 + 3 + … + ( n − 1) + n.
This motivates the following definition
Notation and Definition (sum sequence): Let ( a n ) n ,a n : ℕ → M be a sequence with terms a n , the sum is written:
The sign ∑ is called sigma sign here the index k increases from 1 to n. Sum sequences are sequences whose terms are formed by summation of previous terms.
Thus the n th triangular number can be written as:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Example 3: Sequence of square numbers Interestingly, the sum of two consecutive triangular numbers is a square number. So, for example, we have: 3 + 1 = 4 and 6 + 3 = 9. In general this gives the relationship:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
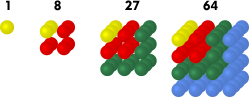
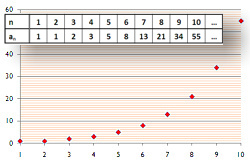
Example 4: Sequence of cube numbers
The first terms of the sequence are: (1 , 8 , 27 , 64 , 125 , … ). |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
If, as in Definition 1, M = ℝ, we obtain the following definition:
Definition 3 (Sequence of Numbers): A sequence of real numbers is a function
When we speak about a sequence in this part of the course we mean in general a real sequence. Note: In this course, we only consider sequences in ℕ , ℚ and ℝ. If we delete arbitrarily many terms from a sequence but retain the order of the remaining sequence, then we obtain a so called subsequence. Mathematically this is defined as follows: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Definition 4 (Subsequence): Given a sequence ( a n ) n and a strictly monotonically increasing
function
we call the composition 2
a subsequence of ( a n ) n .
|
H. Böhm: Relief 6 Punkte ... (1959)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Example 5: Let ( q n ) n with q n := n 2 be the sequence of square numbers
Definition 5 (Sequence of differences):
Given a sequence ( a n ) n = a 1 , a 2 , a 3 , … , a n , …; then 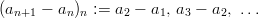 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Example 6: Given the sequence ( a n ) n with a n :=
Let ( b n ) n be its 1 st difference sequence. Then it follows that
A term of ( b n ) n has the general form 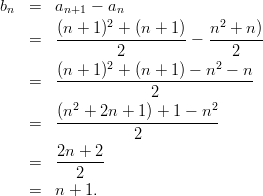
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Exercise 1: Illustrate the sequence of square numbers in at least three different ways. Exercise 2: Let ( π n ) n be the sequence of decimal places of the constant π. Is the finite sequence (1 , 4 , 1 , 5 , 9 , 2) a subsequence ( π n ) n ? Give a reason for your answer.
|


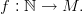


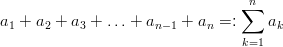
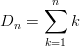
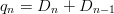

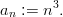
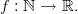
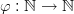
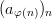

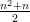 , i.e.
, i.e. 