Grundlagen der anwendungsbezogenen Hochschulmathematik
6. Integralrechnung
6.3. Hauptsatz der Integral und Differentialrechnung

In dem vorherigem Kapitel wurde aus der Kenntnis eines Intervalls \([a,b]\) und einer (stetigen) Funktion \(f\) eine Zahl \(I\) durch die Vorschrift \(I:=\int\limits_a^b f(\xi)\,\mathrm{d}\xi \) definiert. Dieses Vorgehen lässt sich wieder allgemeiner auffassen, indem die obere Integralgrenze als variabel angenommen wird:

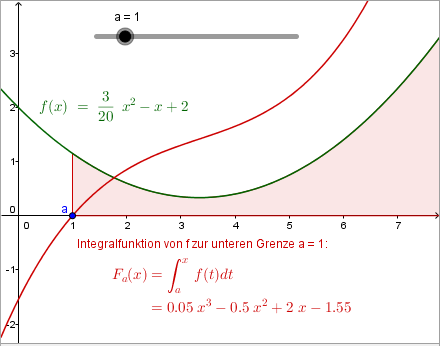
Ist \(f\) über jedem abgeschlossenen Teilintervall von \(I\) integrierbar und ist \(a\in I\), so heißt die Funktion\[F_a(x) = \int^{x}_a f(t)\;dt \text{ für alle } x\in I\]
Integralfunktion von \(f\) zur unteren Grenze \(a\).
Die Stammfunktion
An dieser Stelle soll auch der Begriff der Stammfunktion genannt sein.

Definition 2 (Stammfunktion)
Die reellen Funktionen \(f\) und \(F\) seien auf dem Intervall \((a,b)\) definiert. Gilt für jedes \(x\in(a,b)\) die Gleichung \[F'(x) = f(x),\] so heißt \(F\) die Stammfunktion von \(f\) auf dem Intervall \((a,b)\).
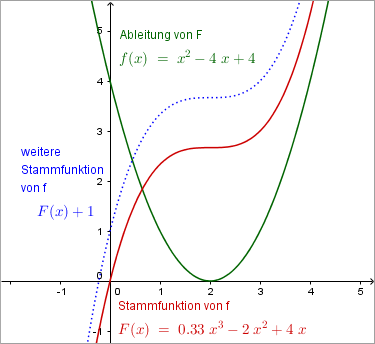
Dabei ist anzumerken, dass es zu jeder Funktion \(f\) unendlich viele Stammfunktionen \(F\) gibt.
Ist \(F\) eine Stammfunktion von \(f\), so sind auch alle durch Addition einer Konstanten erhaltenen Funktionen \(F+c\) Stammfunktionen von \(f\), denn es gilt: \[\frac{d}{dx} (F+c) = \frac{d}{dx} F + \frac{d}{dx} c = f + 0.\]
Umgekehrt unterscheiden sich zwei beliebige Stammfunktionen \(F\) und \(G\) von \(f\) nur durch eine Konstante, d. h. es existiert ein \(c\in\mathbb{R}\), sodass: \(F(x) = G(x) +c.\)
Beispiel 1
Zu \(f(x)=2x\) sind sowohl \(F_0(x) = x^2\) als auch \(F_3 (x) = x^2+3\) oder \(F_{15}(x) = x^2 + 15 \) Stammfunktionen.
Beispiel 2
Die Funktion \(f(x)=e^{x^2}\) ist integrierbar, also für alle \(a\) und \(b\) besitzt das Integral \(\int\limits_a^b e^{\xi^2}\,\mathrm{d}\xi\) einen endlichen Wert. Leider kann aber für die Stammfunktion \(F(x) = \int\limits_a^x e^{\xi^2}\,\mathrm{d}\xi\) keine analytische Darstellung angegeben werden.
Stetige Funktionen besitzen eine Stammfunktion und sind auch integrierbar. Nicht jede riemann-integrierbare Funktion besitzt eine Stammfunktion (z.B: Treppenfunktionen sind integrierbar, können aber keine Stammfunktion besitzen da sie die Zwischenwerteigenschaft nicht erfüllen). Umgekehrt gibt es auch Funktionen, die eine Stammfunktion besitzen, aber nicht riemann-integrierbar sind. Die Existenz einer Stammfunktion ist also nicht äquivalent zur Integrierbarkeit einer Funktion.
Aus der Integrierbarkeit einer Funktion auf einem Intervall folgt die Integrierbarkeit auf Teilintervallen, somit sind für kompakte Intervalle die Integrierbarkeit und die Existenz der Integralfunktion äquivalent.
Der Zusammenhang zwischen Stammfunktion und Integralfunktion wird durch den Hauptsatz der Integral- und Differentialrechnung (HDI) deutlich.

Satz 1 (Hauptsatz der Differential- und Integralrechnung)
- Für \(G(x):=\int\limits_a^x f(\xi)\, \mathrm{d}\xi \) gilt: \[ G'(x) = f(x), \quad x\in(a,b).\]
- Sei \(F\) eine beliebige Stammfunktion der stetigen Funktion \(f\) auf \(D_f\subset\mathbb{R}\), so gilt:
\[I=G(b)=\int\limits_a^b f(\xi)\,\mathrm{d}\xi = [F(\xi)]_a ^b = F(b) - F(a). \]
Beispiel 3
\(\int \limits _0 ^2 f(x)\, \mathrm d x = \int \limits _0 ^2 2x\, \mathrm d x = [x^2-5] _0 ^2 = 2^2 -5-( 0^2-5) = 4\)
(Hierbei wurde als Stammfunktion für \(f(x)=2x\) die Funktion \(x^2-5\) gewählt.)
Dies ist gleichzeitig der Flächeninhalt von \(0\) bis \(2\) unter der Funktion \(2x\).
(Berechnet durch die Dreiecksformel \(\frac{1}{2} \cdot\) Grundlinie \(\cdot\) Höhe \(= \frac{1}{2} \cdot 2 \cdot 4=4\).)
Bemerkung. Die Anwendung des Hauptsatzes funktioniert für jede beliebige Stammfunktion. Stammfunktionen unterscheiden sich nämlich nur durch ein konstantes Glied, das bei der Rechnung verschwindet (wie es im obigen Beispiel mit dem konstanten Glied 5 geschieht).
Neben den bestimmten Integralen der Form \(\int\limits_a^b f(\xi)\,\mathrm{d}\xi\) gibt es auch Integrale der Form \[F(x) = \int f(x)\,\mathrm{d}x.\] Diese Integrale ohne Grenzen heißen unbestimmte Integrale und beschreiben die Menge aller möglichen Stammfunktionen einer Funktion \(f\).

Unbestimmtes Integral
Fehlt im Integral die Angabe von Integrationsgrenzen, so spricht man von einem unbestimmten Integral \(\int f(x)\, \mathrm d x \). Unbestimmte Integrale haben meistens nicht den Zweck, einen bestimmten Flächeninhalt zu berechnen, sondern die Stammfunktion einer Funktion anzugeben.

Ergänzungen zum Hauptsatz der Differential- und Integralrechnung
Bestimmte Integrale können nach dem Hauptsatz mit Hilfe einer beliebigen Stammfunktion berechnet werden.
Der zweite Hauptsatz folgt im Wesentlichen aus dem 1. Hauptsatz, nach dem die Integralfunktion \(F_a\) auch eine Stammfunktion von \(f\) ist, sich also lediglich durch eine additive Konstante \(c\) unterscheidet, d. h. es gilt: \(F(x)=F_a(x)+c\) für alle \(x \in I\).
Einsetzen von \(a\) und \(b\) ergibt:
\(F(a)=F_a(a)+c=c\) und \(F(b)=F_a(b)+c=F_a(b)+F(a)\)
Daraus folgt: \[ \int^{b}_a f(x)\;dx = F_a(b) = F(b) - F(a)\]
Wir hatten die Integralfunktion \(F(x) = \int_a^xf(t)\, \mathrm{d}t\) definiert, wobei \(f\) eine stetige Funktion sei. Es gilt der folgende Satz:

Satz 2 (Differenzierbarkeit der Integralfunktion)
Die Integralfunktion \(F(x)\) ist differenzierbar und es gilt:
\[\frac{d}{dx}F(x) = \frac{d}{dx} \int_a^xf(t)\, \mathrm{d}t = f(x)\]

Bemerkung. Es gibt Funktionen, die integrierbar sind, deren Stammfunktion nicht geschlossen darstellbar ist. So ist die Funktion \[g(x):=e^{-x^2}\] stetig und die Integrale \(\int_a^b e^{-x^2}\,\mathrm{d}x\) existieren, aber es gibt keine geschlossen Darstellung für \(\int e^{-x^2}\,\mathrm{d}x\). Diese Funktion wird auch als Fehlerfunktion bezeichnet
\[\mathrm{erf}(x) = \frac{2}{\sqrt{\pi}}\int_0^x e^{-r^2}\,\mathrm{d}r.\]