Grundlagen der anwendungsbezogenen Hochschulmathematik
5. Differentialrechnung
5.3. Spezielle Ableitungen
In diesem Kapitel beschäftigen wir uns mit speziellen Ableitungen:
- Trigonometrische Funktionen
- verknüpfte Funktionen
- Exponential- und Logarithmusfunktion
Trigonometrische Funktionen
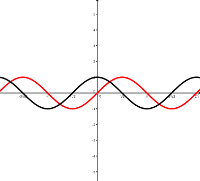
Die Funktion \(\color{red}\sin\color{red}(\color{red}x\color{red})\) und ihre Ableitungs-Funktion \(\cos(x)\).
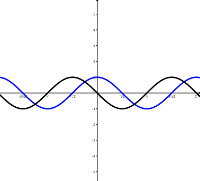
Die Funktion \(\color{blue}\cos\color{blue}(\color{blue}x\color{blue})\) und ihre Ableitungs-Funktion \(-\sin(x)\).
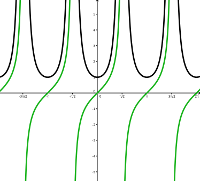
Die Funktion \(\color{green}\tan\color{green}(\color{green}x\color{green})\) und ihre Ableitungsfunktion \(1/\cos^2(x)\).
Beispiel 1:
\[\frac{d}{dx} (3 \sin(x)) = 3 \sin'(x) = 3 \cos(x).\]
Beispiel 2:
\[\frac{d}{dx} \cos^2 (x) = \cos'(x) \cdot \cos(x) + \cos(x) \cdot \cos'(x) = -2\sin(x)\cos(x).\]
Beispiel 3:
\[\begin{aligned} \frac{d}{dx} \frac{\sin(x) + 1}{\cos(x)} &= \frac{d}{dx} \left( \frac{\sin(x)}{\cos(x)} + \frac{1}{\cos(x)} \right) \\ &= \tan'(x) - \frac{\cos'(x)}{\cos^2(x)} \\ &= \frac{1+\sin(x)}{\cos^2 (x)}.\end{aligned}\]
Kettenregel
In diesem Abschnitt lernen wir die Formel zur Bestimmung der Ableitung einer Komposition von Funktionen kennen. Diese wichtige Regel ist bekannt als Kettenregel, damit lassen sich Funktionen wie z.B. \(sin(2x)\) ableiten.
Sei \(f\colon \mathbb{R}\to \mathbb{R}\), \(g\colon \mathbb{R}\to \mathbb{R}\) und \(f \circ g \colon \mathbb{R}\to \mathbb{R}\).
Die Kettenregel.
Sei \(g\) differenzierbar im Punkt \(x\) und \(f\) differenzierbar in \(g(x)\). Dann gilt \[\frac{d}{dx}f(g(x))=f'(g(x))g'(x).\]
Beispiel 1:
Es ist die Funktion \((2x-1)^3\) zu differenzieren. Wir nehmen \(f(x) = x^3\) und \(g(x) = 2x-1\) und differenzieren die Komposition \(f(g(x))\). Da \[f'(x) = 3x^2 \text{ and } g'(x) = 2,\] erhalten wir \[\frac{d}{dx} (2x-1)^3 = 3(2x-1)^2 \cdot 2 = 6(4x^2-4x+1) = 24x^2-24x+6.\]
Die Funktion \(\color{green}(\color{green}2\color{green}x\color{green}-\color{green}1\color{green})^\color{green}3\) und und ihre Ableitungsfunktion.
Beispiel 2:
Wir müssen die Funktion \(\sin 3x\) differenzieren. Nehme \(f(x) = \sin x\) und \(g(x) = 3x\), dann differenziere die Komposition \(f(g(x))\). \[\frac{d}{dx} \sin 3x = \cos 3x \cdot 3 = 3 \cos 3x.\]
Bemerkung. Sei \(h\colon \mathbb{R}\to \mathbb{R}, g\colon \mathbb{R}\to \mathbb{R}\) und \(f\colon \mathbb{R}\to \mathbb{R}\). Nun folgt \[\frac{d}{dx}f(g(h(x)))=f'(g(h(x)))\frac{d}{dx}g(h(x))=f'(g(h(x)))g'(h(x))h'(x).\] Auf ähnliche Weise erhält man komplexere Regeln für Kompositionen von mehreren Funktionen.
Beispiel 3:
Differenziere die Funktion \(\cos^3 2x\). Wähle \(f(x) = x^3\), \(g(x) = \cos x\) und \(h(x) = 2x\) und differenziere die Komposition \(f(g(h(x)))\). \[\begin{aligned}\frac{d}{dx} \cos^3 2x &= 3(\cos 2x)^2 \cdot \frac{d}{dx} \cos 2x \\ &= 3 \cos^2 2x \cdot (-\sin 2x) \cdot 2 \\ &= -6 \sin 2x \cos^2 2x.\end{aligned}\]
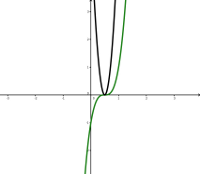
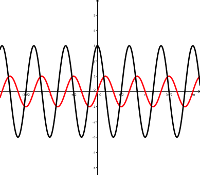Die Funktion \(\color{red}\sin \color{red}3\color{red}x\) und und ihre Ableitungsfunktion.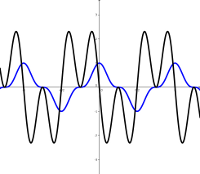 
Die Funktion \(\color{blue}\cos^\color{blue}3 \color{blue}2\color{blue}x\) und und ihre Ableitungsfunktion.
Exponential- und Logarithmusfunktion
Wir definieren zwei wichtige Funktionen, die Exponentialfunktion und die Logarithmusfunktion.
Die Exponentialfunktion
Beispiel 1:
Zum Zeitpunkt \(t_0\) ist die Größe einer Bakterien-Kolonie 500. Die Bakterien teilen sich jede halbe Stunde in zwei. Dies bedeutet, dass sich in einer Stunde die Population vervierfacht:
| nach 1 Stunde | \(4 \cdot 500\) |
|---|---|
| nach 2 Stunden | \(4 \cdot (4 \cdot 500) = 4^2 \cdot 500\) |
| nach 3 Stunden | \(4 \cdot (4^2 \cdot 500) = 4^3 \cdot 500\) |
| \(\vdots\) | \(\vdots\) |
| nach t Stunden | \(4^t \cdot 500\) |
Die Funktion, die die Größe der Bakterien Bevölkerung zum Zeitpunkt \(t\) angibt, ist \(f(t) = 500 \cdot 4^t\).
Modellierung des Bevölkerungs-Wachstums
Zum Zeitpunkt \(t\in \mathbb{R}\) ist die Größe der Bevölkerung \(s(t)\), wobei die Wachstums-Geschwindigkeit direkt proportional ist: \(s'(t)=s(t)\). Sei erst \(s(0)=1\). Nun müssen wir eine Lösung für das Anfangswertproblem finden \[\begin{cases}s'=s, \\ s(0)=1.\end{cases}\]
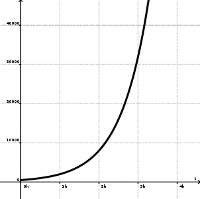
Die Funktion \(500 \cdot 4^t\).
Definition 1 (Exponentialfunktion)
\[\exp(t):=\sum_{k=0}^{\infty} \frac{t^k}{k!}.\]
Die Motivation für diese Definition ist die formale Rechnung \[ \frac{d}{dt}(1+t+\frac{1}{2!}t^2+\frac{1}{3!}t^3+\dots ) = 1+t+\frac{1}{2!}t^2+\frac{1}{3!}t^3+\dots,\] wobei wir die Umformung \( \frac{k}{k!} = \frac{1}{(k-1)!}\) nutzen.
Man kann zeigen, dass die Reihe konvergiert für alle \( t\in\mathbb{R}\) und die Funktion exp die notwendigen Eigenschaften besitzt. Die Beweise sind eher technisch und werden hier weggelassen.
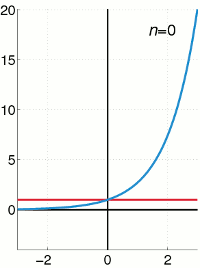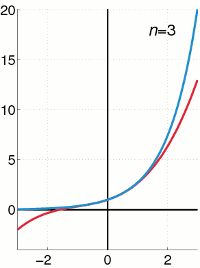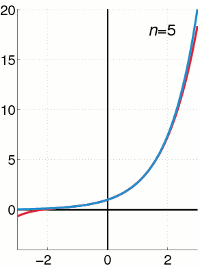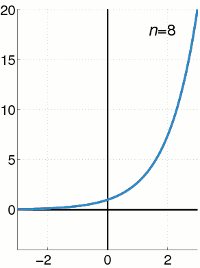
Die Funktion \(e^t\) und die Summe der ersten \(n+1\) Terme von \(\sum_{k=0}^{\infty} \frac{t^k}{k!}.\)
Satz 1.
Für alle \(t\in \mathbb{R}\) haben wir \( \exp (t) = e^t \), mit \( e=\exp(1)\) als sogenannte Napiers Konstante oder Eulersche Zahl.
Satz 2.
\[\frac{d}{dx}\exp(x)=\exp(x).\]
Interaktivität. Die Ableitung der Exponentialfunktion (Der Punkt \( x \) ist waggrecht verschiebbar).
Der natürliche Logarithmus
Anhand der Formel \( \exp (x)=e^x\) sehen wir, dass \(\exp \colon \mathbb{R} \to (0,\infty)\) eine strikt steigende (somit bijektive) Funktion ist. Ihre Inverse heißt natürlicher Logarithmus:
Definition 2
\[\ln:=\exp^{-1}\colon (0,\infty)\to \mathbb{R}.\]
Beispiel 3.
Aus der Definiton erhalten wir \(\exp(\ln(x)) = x\), für \(x>0\). Also \[\begin{aligned}\frac{d}{dx} \exp(\ln(x)) &= \frac{d}{dx}x \\ \exp(\ln(x)) \cdot \frac{d}{dx} \ln(x) &= 1 \\ x \cdot \frac{d}{dx} \ln(x) &= 1 \\ \frac{d}{dx} \ln(x) &= \frac{1}{x} \text{, für } x>0.\end{aligned}\]
Somit haben wir gezeigt:
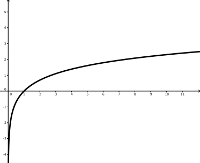
Natürliche Logarithmus-Funktion \(\ln(x)\).
Satz 3.
\[\frac{d}{dx} \ln(x) = \frac{1}{x}, \text{ wenn } x>0.\]
Interaktivität. Die Ableitung der Logarithmusfunktion.
Exponentialfunktion mit Basis \( a > 0\)
Beispiel 4.
Per Definition \(a^x = \exp(x \ln(a))\). Somit \[\begin{aligned}\frac{d}{dx} a^x &= \frac{d}{dx} \exp(x \ln(a)) \\ &= \exp(x \ln(a)) \cdot \frac{d}{dx} (x \ln(a)) \\ &= a^x \ln(a) \text{, für } a > 0.\end{aligned}\] Somit haben wir bewiesen:
Satz 4.
\[\frac{d}{dx} a^x = a^x \ln(a) \text{, wenn } a > 0\]
Logarithmus mit Basis \(a > 0\)
Die Funktion \((t\mapsto a^t)\colon \mathbb{R} \to (0,\infty)\) ist
-
strikt monoton fallend für \(0 \lt a \lt 1\), und
-
strikt monoton steigend für \(1 \lt a \lt \infty\).
Dann heißt die Inverse Logarithmus mit der Basis \(a\):
Definition 3
\[\log_a \colon (0, \infty) \to \mathbb{R}\]
Satz 5.
Für \(x>0\) \[\frac{d}{dx} \log_a(x) = \frac{1}{x \ln(a)}.\]
Der Logarithmus hat die folgenden Eigenschaften (sofern der jeweilige Logarithmus definiert ist):
Satz 6.
-
\(\log_a(1) = 0\)
-
\(\log_a(a) = 1\)
-
\(\log_a(x^r) = r \log_a(x)\)
-
\(\log_a(a^x) = x\)
-
\(\log_a(x) = \frac{\log_b(x)}{\log_b(a)}\)
-
\(\log_a(xy) = \log_a(x)+\log_a(y)\)
-
\(\log_a(\frac{x}{y}) = \log_a(x)-\log_a(y)\)