Grundlagen der anwendungsbezogenen Hochschulmathematik
5. Differentialrechnung
5.1. Grundlagen

Definition

Ableitung - Definitionen und Grundlagen
Als nächstes folgt die Definition der Ableitung einer Funktion. Hierbei starten wir mit einem Beispiel, um die Idee hinter der formalen Definition zu veranschaulichen
Beispiel 0:
Der folgende Graph gibt an, wie weit ein Fahrradfahrer von seinem Startpunkt aus gelangt.
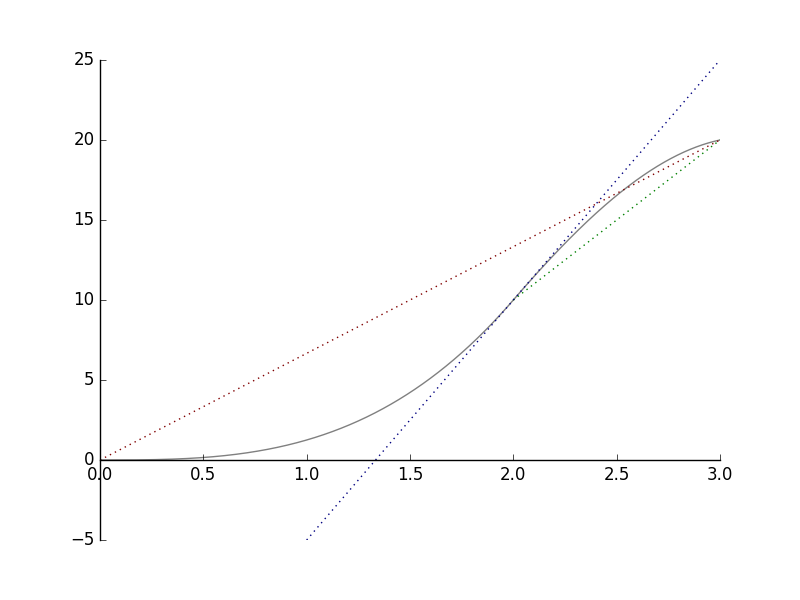
- Betrachte die rote Linie. Man erkennt, dass der Radfahrer innerhalb von 3 Stunden \(20\) km zurücklegt. Die durchschnittliche Geschwindigkeit der gesamten Strecke beträgt \(6.6\) km/h.
- Betrachte nun die grüne Linie. Innerhalb der zweiten und dritten Stunde legt der Radfahrer weitere \(10\) km zurück. Somit ist in diesem Zeitintervall die durchschnittliche Geschwindigkeit \(10\) km/h.
Hierbei betragen die Steigung der roten Linie \(\frac{20}{3} \approx 6.6\) und die Steigung der grünen Linie \(10\). Diese Werte entsprechen den zugehörigen Durchschnitts-Geschwindigkeiten. - Betrachte noch die blaue Linie. Sie ist die Tangente der Kurve im Punkt \(x=2\) h. Durch Anwendung des gleichen Prinzips wie mit durchschnittlichen Geschwindigkeiten, schließen wir, dass 2 Stunden nach der Abfahrt, die Geschwindigkeit der Radfahrers \(\frac{30}{2}\) km/h \(= 15\) km/h betrug.
Führt man diesen Gedankengang ins unendlich Kleine fort, dann kommt man zur allgemeinen Definition der Ableitung:

Definition 1 (Ableitung)
Sei \((a,b)\subset \mathbb{R}\). Die Ableitung der Funktion \(f\colon (a,b)\to \mathbb{R}\) im Punkt \(x_0\in (a,b)\) ist definiert als \[f'(x_0):=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}.\] Wenn \(f'(x_0)\) existiert, dann heißt \(f\) differenzierbar im Punkt \(x_0\).
Bemerkung: Da \(x = x_0+h\), folgt \(h=x-x_0\), und somit kann die Definition auch in der äquivalenten Form \[f'(x_0):=\lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0}\] geschrieben werden.
Es gibt verschiedene Möglichkeiten die Ableitung zu notieren:
\[f'(x_0)=Df(x_0) =\left. \frac{df}{dx}\right|_{x=x_0}, \ \ f'=Df =\frac{df}{dx}. \]
Geometrische Interpretation
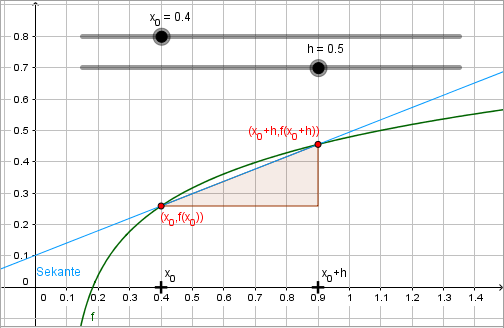
Betrachte die Kurve \(y = f(x)\). Legt man eine Gerade durch die Punkte \((x_0,f(x_0))\) und \((x_0+h, f(x_0+h))\), so beträgt die Steigung der Kurve \[\frac{f(x_0+h)-f(x_0)}{x_0+h-x_0} = \frac{f(x_0+h)-f(x_0)}{h}.\] Wenn \(h \to 0\) definieren wir den Grenzfall als Tangente in diesem Punkt. Die Gerade berührt die Kurve \(y = f(x)\) nur im Punkt \((x_0, f(x_0))\). Die Gerade ist die Tangente an die Kurve \(y=f(x)\) im Punkt \((x_0,f(x_0))\) und ihre Steigung beträgt \[\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h},\] welches der Ableitung der Funktion \(f\) im Punkt \( x_0\) entspricht. Somit ist die Tangente durch die Gleichung \[y=f(x_0)+f'(x_0)(x-x_0)\] gegeben.
Interaktivität. Manipuliere die Werte für \(x_0\) und betrachte die Änderungen der Tangente an der Kurve.
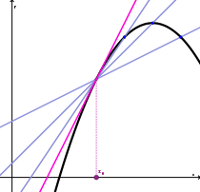
geometrische Interpretation
Beispiel 1:
Sei \(f\colon \mathbb{R} \to \mathbb{R}\) die Funktion \(f(x) = x^3 + 1\). Die Ableitung von \(f\) in \(x_0 = 1\) beträgt: \[\begin{aligned}f'(1) &=\lim_{h \to 0} \frac{f(1+h)-f(1)}{h} \\ &=\lim_{h \to 0} \frac{(1+h)^3 + 1 - 1^3 - 1}{h} \\ &=\lim_{h \to 0} \frac{1+3h+3h^2+h^3-1}{h} \\ &=\lim_{h \to 0} \frac{h(3+3h+h^2)}{h} \\ &=\lim_{h \to 0} 3+3h+h^2 \\ &= 3. \end{aligned}\]
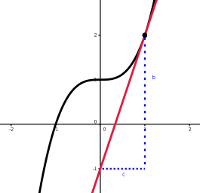
Die Funktion \( x^3 + 1\) und ihre Tangente im Punkt \(1\).
Beispiele zur elementaren Berechnung der Ableitung bei verschiedenen Funktionen
Beispiel 2:
Sei \(g\colon \mathbb{R} \to \mathbb{R}\) die Funktion \(g(x)=|x|\). Hat \(g\) eine Ableitung im Punkt \(0\)?
Nun ist \[g'(x_0)= \begin{cases}+1 & \text{wenn $x_{0}>0$} \\ -1 & \text{wenn $x_{0}<0$}\end{cases}\]
Der Graph \(y=g(x)\) hat keine Tangente im Punkt \(x_0=0\): \[\frac{g(0+h)-g(0)}{h}= \frac{|0+h|-|0|}{h}=\frac{|h|}{h}=\begin{cases}+1 & \text{für $h>0$}, \\ -1 & \text{für $h<0$}.\end{cases}\] Folglich existiert \(g'(0)\) nicht.
Ergebnis. Die Funktion \(g\) ist nicht differenzierbar im Punkt \(0\).
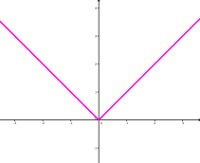
Die Funktion \(|x|\).
Bemerkung. Sei \(f\colon (a,b)\to \mathbb{R}\). Wenn \(f'(x)\) für jedes \(x\in (a,b)\) existiert, dann erhalten wir die Funktion \(f'\colon (a,b)\to \mathbb{R}\). Wir schreiben:
| (1) | \(f(x)\) | = \(f^{(0)}(x)\), | |
| (2) | \(f'(x)\) | = \(f^{(1)}(x)\) | = \(\frac{d}{dx}f(x)\), |
| (3) | \(f''(x)\) | = \(f^{(2)}(x)\) | = \(\frac{d^2}{dx^2}f(x)\), |
| (4) | \(f'''(x)\) | = \(f^{(3)}(x)\) | = \(\frac{d^3}{dx^3}f(x)\), |
| ... |
Hier ist \(f''(x)\) die zweite Ableitung von \(f\) in \(x\), \(f^{(3)}\) ist die dritte Ableitung und so weiter.
Wir führen folgende Notation ein: \begin{eqnarray} C^n\bigl( (a,b)\bigr) =\{ f\colon \, (a,b)\, \to \mathbb{R} & \mid & f \text{ ist } n \text{ mal differenzierbar im Intervall } (a,b) \nonumber \\ & & \text{ und } f^{(n)} \text{ ist stetig}\}. \nonumber \end{eqnarray} Diese Funktionen sind n-mal stetig differenzierbar.
Eine praktische Anwendung für höhere Ableitungen sehen Sie in Die Änderungsrate aus physikalischer Sicht und eine innermathematische Anwendung im späteren Kapitel Kurvendisskussion.

Linearisierung und Differenzial
Die Ableitung dient auch dazu Funktionen zu approximieren. Aus der Definition der Ableitung erhalten wir \[ f'(x_0)\approx \frac{f(x)-f(x_0)}{x-x_0} \Leftrightarrow f(x)\approx f(x_0)+f'(x_0)(x-x_0), \] wobei die rechte Seite die Linearisierung oder das Differenzial von \(f\) in \(x_0\) ist. Das Differenzial wird mit \(df\) bezeichnet. Der Graph der Linearisierung, \[ y=f(x_0)+f'(x_0)(x-x_0), \] ist die Tangente vom Graph der Funktion \(f\) im Punkt \((x_0,f(x_0))\). Später, in der Analysis mit mehreren Variablen, wird die tatsächliche Bedeutung des Differenzials klarer. Für das Erste, sind die genauen Details nicht notwendig. Dies motiviert eine äquivalente Definition der Ableitung:
\(f\) heißt differenzierbar an der Stelle \(x_0\), wenn eine Zahl existiert, sodass gilt:
\[ f(x) = f(x_0) + m\cdot (x-x_0) + r(x-x_0),\]
wobei für die Restfunktion \(r\) gilt:
\[ \lim\limits_{x \to x_0} \frac{ r(x-x_0)}{x-x_0} = 0 \]
\(m\) wird dann Ableitung von \(f\) an der Stelle \(x_0\) genannt; \(f'(x_0)=:m\).
Zur Vermeidung des Quotienten im Grenzwert lässt sich stattdessen auch definieren:
\[ f(x) = f(x_0) + m\cdot (x-x_0) + (x-x_0) \cdot R(x-x_0), \]
wobei
\[ \lim\limits_{x \to x_0} R(x-x_0) = 0 \]
Bedeutung der Definition:
Für lineare Funktionen lässt sich jeder Funktionswert \(f(x)\) aus dem Funktionswert an einer festen Stelle \(x_0\) berechnen, indem die Differenz \(x-x_0\) mit der Steigung \(m\in\mathbb{R}\) multipliziert wird:
\[f(x)=f(x_0) + (x-x_0)\cdot m.\]
Bei nichtlinearen Funktionen muss die Steigung in Abhängigkeit von der Stelle modifiziert werden, doch lokal passt die Approximation gut, sofern die Modifikation \(R(x-x_0)\) lokal klein ist und im Grenzwert verschwindet, d.h.:
\[ f(x) = f(x_0) + (x-x_0) \cdot (m + R(x-x_0)) \text{ mit } \lim\limits_{x \to x_0} R(x-x_0) = 0.\]

Anschauliche/graphische Beziehung zwischen Funktionsgraph und Ableitung
Graphisch differenzieren
Vom Verständnis der Ableitung als Tangentensteigung ausgehend kann ohne formale Berechnungs-Verfahren graphisch differenziert werden. Dazu muss an einzelnen Punkten des Graphen einer Funktion die Steigung ermittelt werden (z.B. durch Anlegen einer Tangente). Der (gemessene) Wert für deren Steigung wird als Ordinate (y-Wert) – gemeinsam mit der zugehörigen Abszisse (x-Wert) – als Punkt in ein (zweites) Koordinatensystem übertragen.
Verschieben Sie den Punkt A entlang des Graphen. Im linken Fenster wird der Wert der Tangentensteigung an diesem Punkt eingezeichnet.Vorstellungen
Es gibt verschiedene Möglichkeiten die Ableitung zu interpretieren:
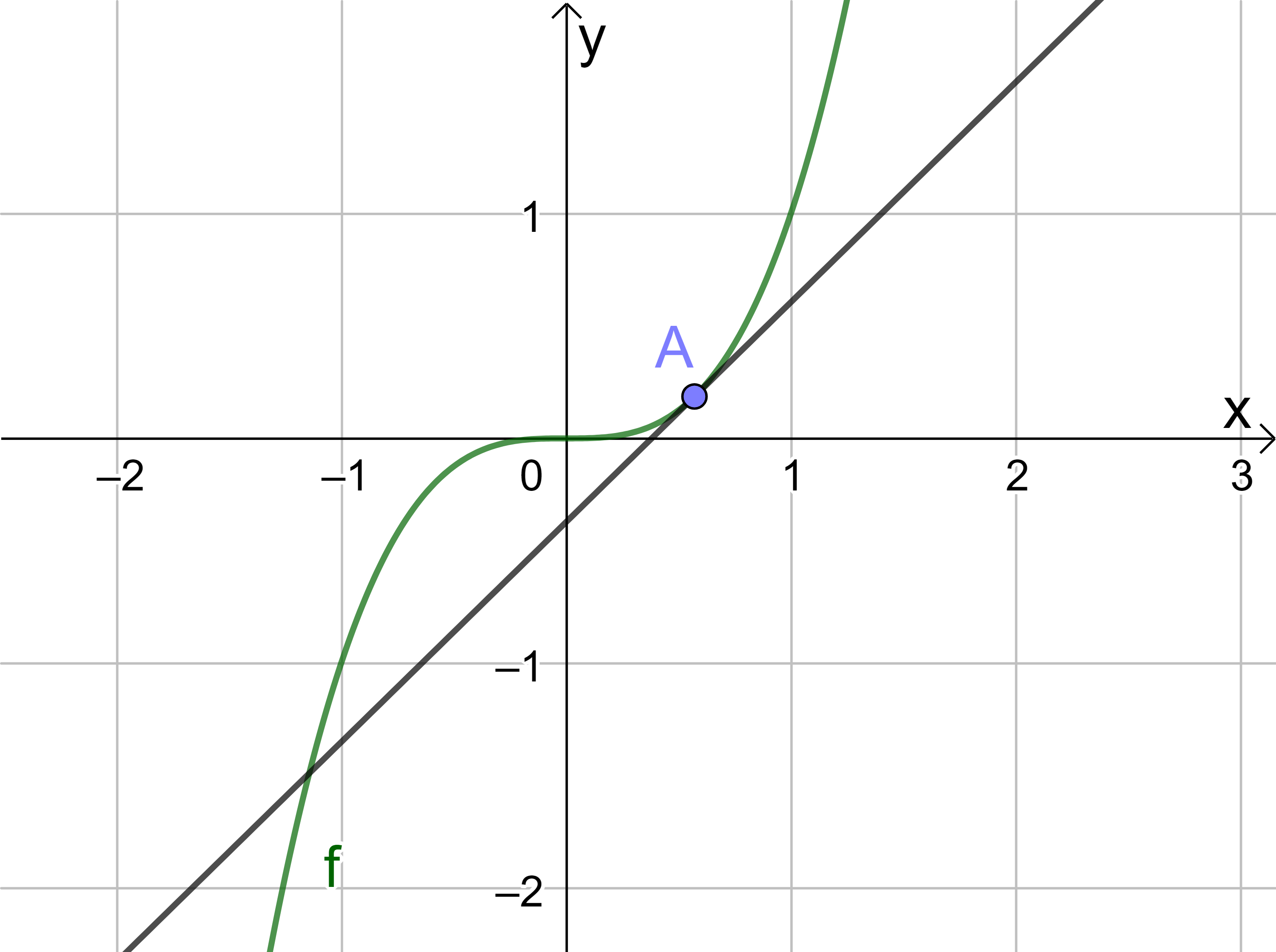
Im folgenden betrachten wir die unterhalb der Definition beschriebene Interpretation die Ableitung als die Steigung der Tangenten an den Punkt einer differenzierbaren Funktion verstehen. Hierbei darf die Tangente aber - anders als beim Kreis - den Funktionsgraphen durchaus mehrmals schneiden wie das Beispiel rechts zeigt.
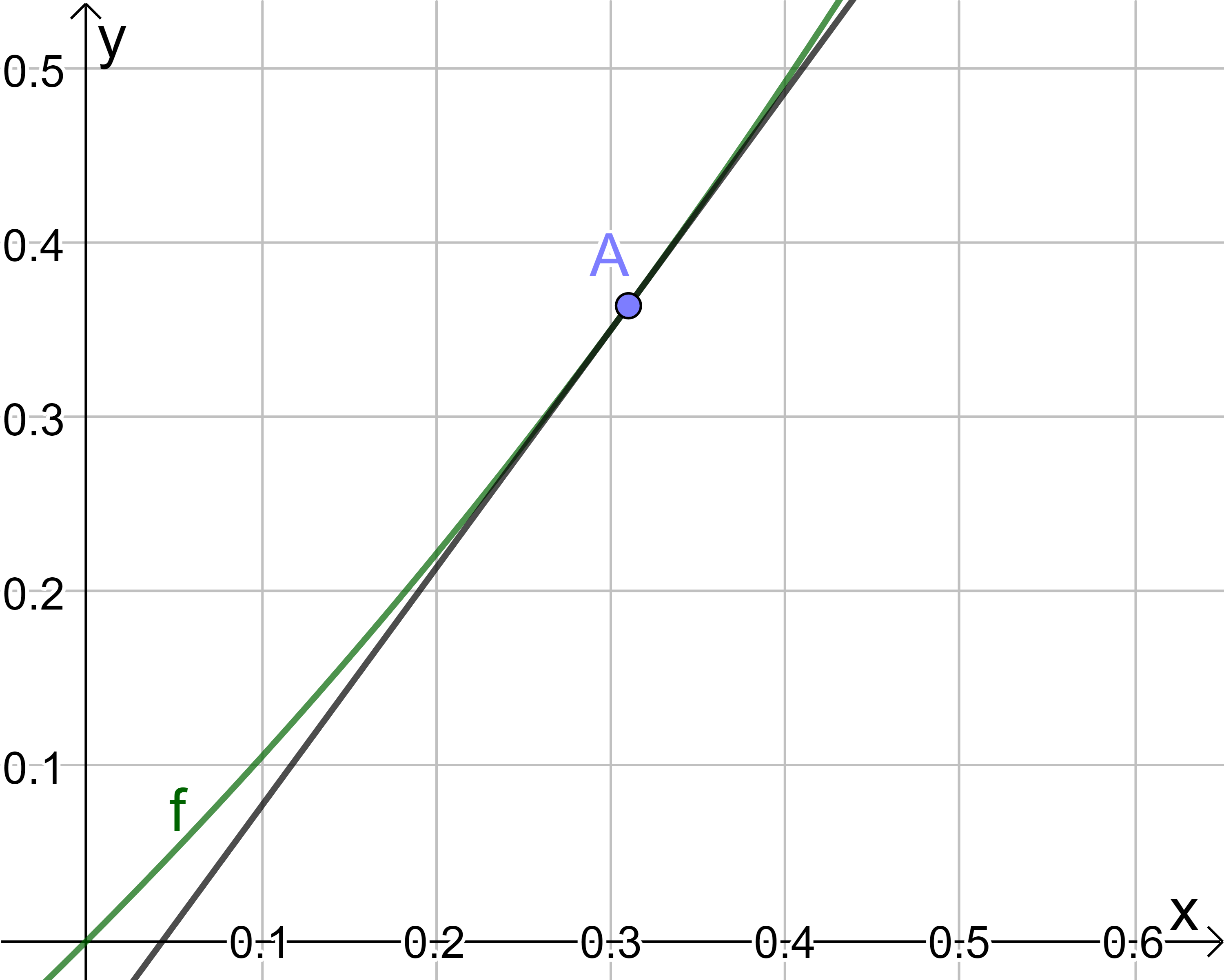
Vielmehr schmiegt sich die Tangente in diesem einen Punkt der Gerade an, wenn man beliebig weit hineinzoomt. Man kann sich deshalb besser eine Schmiegegerade statt einer Tangenten vorstellen.
Die Tangente und die Kurve im gemeinsamen Punkt haben dabei die gleiche Steigung. Zusätzlich kann man anhand der Kurve die "lokale Richtung" der Kurve ablesen. In obigem Fall steigt die Kurve in einer gewissen Steigung
Ableitung als lokale Änderungsrate
Betrachten wir nochmals das Beispiel 0, dann tauchen hier mehrere Arten von Änderungsraten auf (Der Graph sei durch die Funktion \( f \) gegeben). Die Angabe der insgesamt zurückgelegten Strecke von 20 km durch die Betrachtung der Differenz \( f(3) - f(0) \) ist eine absolute Änderungsrate. Berücksichtigt man zusätzlich die benötigte Zeit, indem man mittels Steigungsdreieck die Steigung bzw. mittlere Geschwindigkeit berechnet, so ist dies eine mittlere Änderungsrate. In unserem Fall war das der Differenzenquotient \( \frac{f(3)-f(0)}{3-0}=\frac{20}{3} \).
Verkleinert man systematisch das Intervall auf der \( x \)-Achse (in unserem Fall die Zeit), so erhält man die lokale Änderungsrate bzw. den Differentialquotienten aus der Definition der Ableitung. Dieser spiegelt nicht mehr die mittlere Geschwindigkeit, sondern die Momentantgeschwindigkeit in einem Punkt wider bzw. allgemeiner die Steigung einer Kurve in einem Punkt.
Wichtig ist dabei zu verinnerlichen, dass der Differenzenquotient ein Quotient und der Differentialquotient der Grenzwert eines Quotienten ist.
Ableitung als lokale lineare Approximation
Wir haben bereits gesehen, dass Graphen differenzierbarer Funktionen Schmiegegeraden besitzen. Wie man den Funktionsterm der Tangenten bestimmt, wurde unter Linearisierung und Differential bereits angesprochen. Wenn wir wieder das Beispiel aus der "Ableitung als Tangentensteigung" betrachten und noch viel weiter hineinzoomen würden, so könnten wir irgendwann kaum mehr zwischen Kurve und Tangente unterscheiden - der Graph der Kurve ist also für kleine Abweichungen des \( x \)-Wertes vom Schnittpunkt linear. Man kann also für diese \( x \)-Werte statt des möglicherweise komplizierten Funktionsterms der Kurve die einfachere Linearisierung als gute Näherung nutzen.
Diese Eigenschaft nutzt man z.B. bei der Kleinwinkelnäherung. Dabei können die trigonometrischen Funktionen Sinus, Kosinus und Tangens für Winkel nahe \( 0 \) linearisiert werden. So ist \( sin(x) \approx x \approx tan(x) \) sowie \( cos(x) \approx 1 \) für sehr kleine \(x\). Dies ist graphisch anschaulich, wenn man in den entsprechenden Graphen hineinzoomt, und kann z.B. mittels derer Taylor-Entwicklungen bewiesen werden.