In diesem Abschnitt lernen Sie ausgewählte Kurven, wie etwa Kreis und Ellipse kennen.
Grundlagen der anwendungsbezogenen Hochschulmathematik
متطلبات الإكمال
4. Funktionen II
4.6. Kurven und Abbildungen


Parametrisierte Kurven
Definition (Kurven)
Eine parametrisierte Kurve \(K\) ist eine Abbildung der Form
\( K:[a,b] \rightarrow \mathbb{R}^2\)
\(t \rightarrow (K_1(t),K_2(t)) = (x(t),y(t))\)
wobei \(t \in [a,b] \subset \mathbb{R}\); man nennt \(t\) den Parameter.
Eine parametrisierte Kurve \(K\) ist eine Abbildung der Form
\( K:[a,b] \rightarrow \mathbb{R}^2\)
\(t \rightarrow (K_1(t),K_2(t)) = (x(t),y(t))\)
wobei \(t \in [a,b] \subset \mathbb{R}\); man nennt \(t\) den Parameter.
Die implizite Darstellung einer Kurve \(K\) erhält man als die Nullstellenmenge einer Gleichung:
\(K:\{(x,y) | f(x,y) = 0\}\)

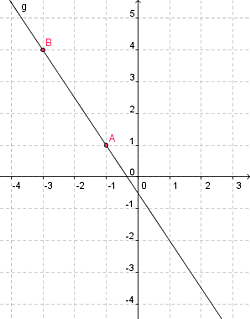
Kurven darstellen - Gerade
Die Gerade \(g\) durch die Punkte \(A = (-1,1)\) und \(B = (-3,4)\) besitzt folgende Parameterdarstellung:
\((x = - 1 + t(- 3 - (- 1)), y = 1 + t(4 - 1))\)
also \((x = - 1 - 2t, y = 1 + 3t)\).
Die Parameterdarstellung ist dabei allgemein von der Form:
\(x = x_1 + t(x_2 - x_1), y = y_1 + t(y_2 - y_1)\), für alle \(t \in \mathbb{R} \)
In impliziter Form wird die Gerade \(g\) durch eine Gleichung ausgedrückt:
\((4 - 1)(x - (- 1)) = (- 3 - (- 1))(y - 1)\)
also \(3x + 2y + 1 = 0\)
Dies ergibt sich aus der allgemeinen Form
\((y - y_1) = m \cdot (x - x_1)\)
Darin ist \(m \in \mathbb{R}\) die sog. Steigung der Geraden, die sich per
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
berechnen lässt.
Die Gerade \(g\) durch die Punkte \(A = (-1,1)\) und \(B = (-3,4)\) besitzt folgende Parameterdarstellung:
\((x = - 1 + t(- 3 - (- 1)), y = 1 + t(4 - 1))\)
also \((x = - 1 - 2t, y = 1 + 3t)\).
Die Parameterdarstellung ist dabei allgemein von der Form:
\(x = x_1 + t(x_2 - x_1), y = y_1 + t(y_2 - y_1)\), für alle \(t \in \mathbb{R} \)
In impliziter Form wird die Gerade \(g\) durch eine Gleichung ausgedrückt:
\((4 - 1)(x - (- 1)) = (- 3 - (- 1))(y - 1)\)
also \(3x + 2y + 1 = 0\)
Dies ergibt sich aus der allgemeinen Form
\((y - y_1) = m \cdot (x - x_1)\)
Darin ist \(m \in \mathbb{R}\) die sog. Steigung der Geraden, die sich per
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
berechnen lässt.

Kurven darstellen - Kreis
Definition (Kreis)
Ein Kreis ist die Menge aller Punkte \(P\), die von einem vorgegebenen Punkt \(M\) einen festen Abstand \(r\) haben, also
\(\{P \mid |P M | = r\}\)
Der Kreis ist durch die Angabe des Punktes \(M\), seines Mittelpunktes, und seines Radius’ \(r\) vollständig bestimmt.
Ein Kreis ist die Menge aller Punkte \(P\), die von einem vorgegebenen Punkt \(M\) einen festen Abstand \(r\) haben, also
\(\{P \mid |P M | = r\}\)
Der Kreis ist durch die Angabe des Punktes \(M\), seines Mittelpunktes, und seines Radius’ \(r\) vollständig bestimmt.
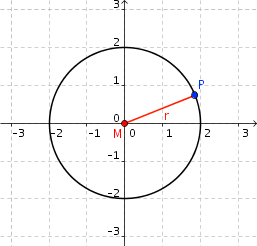
In impliziter Form lässt sich ein Kreis um den Nullpunkt \(M = (0, 0)\) mit dem Radius \(r = 2\) schreiben als
\(x^2 + y^2 = 2^2\)
Alternativ, aber äquivalent hierzu, lässt sich ein Kreis auch in Parameterform darstellen:
\((2 \cdot \cos(t), \,2 \cdot \sin(t)), 0 \le t < 2\pi \)

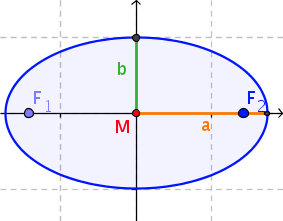
Kurven darstellen - Ellipsen
Der Kreis (rot) ist ein Spezialfall der Ellipse (blau) (vgl. Animation).
Der Kreis (rot) ist ein Spezialfall der Ellipse (blau) (vgl. Animation).

Definition: Ellipse
Eine Ellipse ist die Menge aller Punkte \(P\), deren Abstandssumme von zwei gegebenen Punkten \(F_1\) und \(F_2\), den sog. Brennpunkten, konstant ist. Also
\(\{P \mid |P F_1| + |PF_2| = const.\}\)
Eine Ellipse ist die Menge aller Punkte \(P\), deren Abstandssumme von zwei gegebenen Punkten \(F_1\) und \(F_2\), den sog. Brennpunkten, konstant ist. Also
\(\{P \mid |P F_1| + |PF_2| = const.\}\)
Hier sehen Sie die sog. Gärtnerkonstruktion einer Ellipse. Ziehen Sie mit der Maus am roten Punkt \(P\) und verändern Sie die Lage der Brennpunkte \(F_1\) und \(F_2\) mit dem orangen Schieberegler:
Jeder Punkt \(P = (x,y)\) einer Ellipse mit den Halbachsen \(a\) und \(b\) (vgl. Zeichnung rechts) erfüllt die Gleichung:
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} =1\)
Dies ist die Ellipsengleichung für eine Ellipse mit Mittelpunkt \((0, 0)\) in kartesischen Koordinaten. Die Parameterform dazu lautet:
\((a \cdot \cos(t), b \cdot \sin(t)), 0 \le t < 2\pi\)
\(\frac{x^2}{a^2} + \frac{y^2}{b^2} =1\)
Dies ist die Ellipsengleichung für eine Ellipse mit Mittelpunkt \((0, 0)\) in kartesischen Koordinaten. Die Parameterform dazu lautet:
\((a \cdot \cos(t), b \cdot \sin(t)), 0 \le t < 2\pi\)
Ein weiteres Beispiel: Die Zykloiden
Wenn ein Rad vom Radius \(r\) auf einer ebenen Fläche entlang rollt (z. B. ein Autoreifen) ohne dabei zu gleiten und dabei die Bewegung eines Punktes \(P\) auf dem Rad aufgezeichnet wird (z. B. die Bewegung des Ventils), dann ist die Bahnkurve des Punktes \(P\) eine sog. Zykloide.
Als Parameter wählt man hier den Abstand \(a = |MP|\) von Mittelpunkt \(M\) des Rades zum betrachteten Punkt \(P\) und den sog. Wälzwinkel \(t\). Die Parameterdarstellung der Kurve lautet dann:
\((r \cdot t - a \cdot \sin(t), r - a \cdot \cos(t))\)
Abhängig von der Lage des Punktes \(P\) erhält man verschiedene Typen von Zykloiden: Wenn \(a = r\) heißt die Kurve gewöhnliche Zykloide, wenn \(a > r\) verschlungene Zykloide und sonst (\(a < r\)) gestreckte Zykloide.
Wenn ein Rad vom Radius \(r\) auf einer ebenen Fläche entlang rollt (z. B. ein Autoreifen) ohne dabei zu gleiten und dabei die Bewegung eines Punktes \(P\) auf dem Rad aufgezeichnet wird (z. B. die Bewegung des Ventils), dann ist die Bahnkurve des Punktes \(P\) eine sog. Zykloide.
Als Parameter wählt man hier den Abstand \(a = |MP|\) von Mittelpunkt \(M\) des Rades zum betrachteten Punkt \(P\) und den sog. Wälzwinkel \(t\). Die Parameterdarstellung der Kurve lautet dann:
\((r \cdot t - a \cdot \sin(t), r - a \cdot \cos(t))\)
Abhängig von der Lage des Punktes \(P\) erhält man verschiedene Typen von Zykloiden: Wenn \(a = r\) heißt die Kurve gewöhnliche Zykloide, wenn \(a > r\) verschlungene Zykloide und sonst (\(a < r\)) gestreckte Zykloide.


