Grundlagen der anwendungsbezogenen Hochschulmathematik
3. Funktionen I
3.1. Grundlagen zu Funktionen


Funktionen
In diesem Kapitel wird der Funktionsbegriff definiert und erläutert. Im Anschluss daran werden verschiedene bereits aus der Schule bekannte Funktionen eingehend betrachtet.
Was ist eine Funktion?
Isaac Newton (1643–1727) ist einer der Begründer der Differenzial- und Integralrechnung, die wir im Laufe des Kurses noch kennenlernen werden. Er untersuchte „Größen“ in geometrischen und in physikalischen Situationen, die mit der Zeit „fließen“. Mit dem Wort "fließen" meinte Newton damals, dass sich die Punkte mit der Zeit verändern. Er schreibt dazu selbst:
"Ich betrachte hier die mathematischen Größen [. . . ] durch stetige Bewegung beschrieben. [. . . ] Diese Erzeugungen finden in der Natur tatsächlich statt, und man kann sie täglich bei der Bewegung der Körper beobachten. (Newton 1704)"
Interpretiert man den Begriff Zeit abstrakter, dann entspricht das einer Größe t, die sich mit konstanter Geschwindigkeit stetig ändert und von der andere Größen x.t/, y.t/, . . . abhängt. Betrachten wir ein Beispiel zu einer Funktion:

Beispiel 1
Zwischen der in Metern pro Sekunde gemessenen Schallgeschwindigkeit \(c\) und der in Grad Celsius gemessenen Lufttemperatur \(\theta\) besteht der Zusammenhang
\(c(\theta) = 331,5 \cdot \sqrt{1 + \frac{\theta}{273} }\, \text{für } \, \theta > - 273\)
\(c\) ist eine Funktion von \(\theta\).

Definition Funktion:
Zu beliebigen Mengen \(A\) und \(B\) versteht man unter einer Funktion (bzw. Abbildung) \(f : A \rightarrow B\) eine Vorschrift, die jedem(!) \(x \in A\) genau einen Funktionswert \(y = f(x) \in B\) zuordnet. \(A\) heißt dabei Definitions- und \(B\) Zielmenge.
Für jedes \(x \in A\) heißt das dem Element \(x \) zugeordnete Element \(y \in B\) Funktionswert von \(x \). Die Menge aller Funktionswerte nennt man Wertemenge der Funktion. Mit dem maximalen Definitionsbereich einer Funktion auf einer Grundmenge bezeichnen wir alle Werte der Grundmenge in denen die Funktion wohldefiniert ist.
Der Graph von \(f\) ist die Menge \(G_f= \{(x,y) \in A × B : y = f(x)\}\)
Diese Schreibweise bedeutet, dass die Funktionsvorschrift \(f \) einem Wert \(x\) (dem „Urbild“) einen Funktionswert \(f(x)\) (das „Bild“) zuordnet. Dabei können Funktionen auch auf diskreten Mengen definiert sein, beispielsweise kann auch eine Folge als Funktion auf den natürlichen Zahlen aufgefasst werden. Eine solche Funktion nennt man diskrete Funktion.
Erklärung: Eine Funktion ist also eine eindeutige Zuordnungs-Vorschrift.
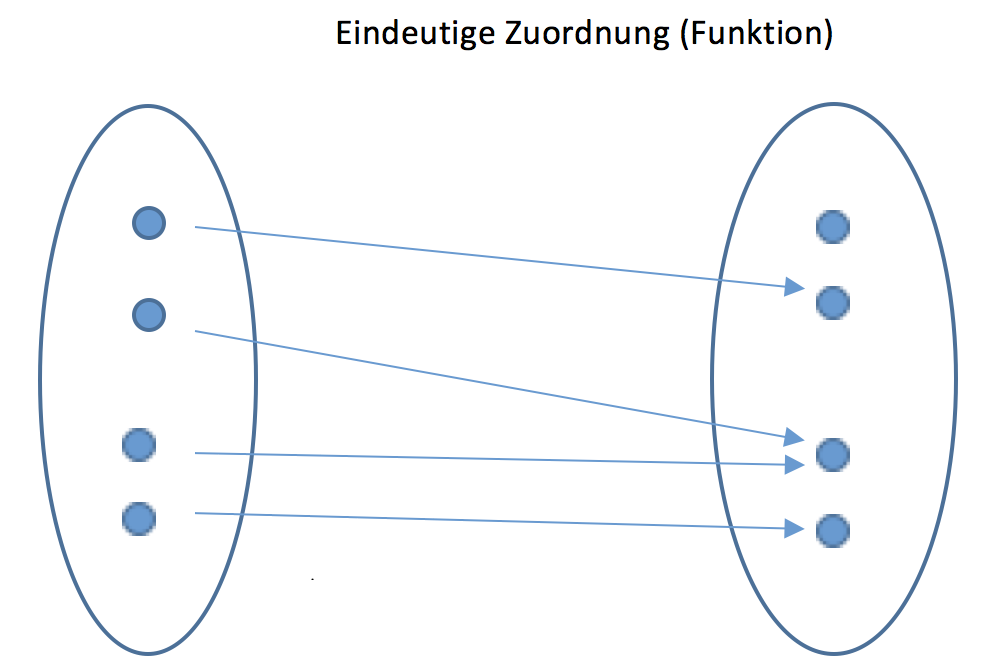
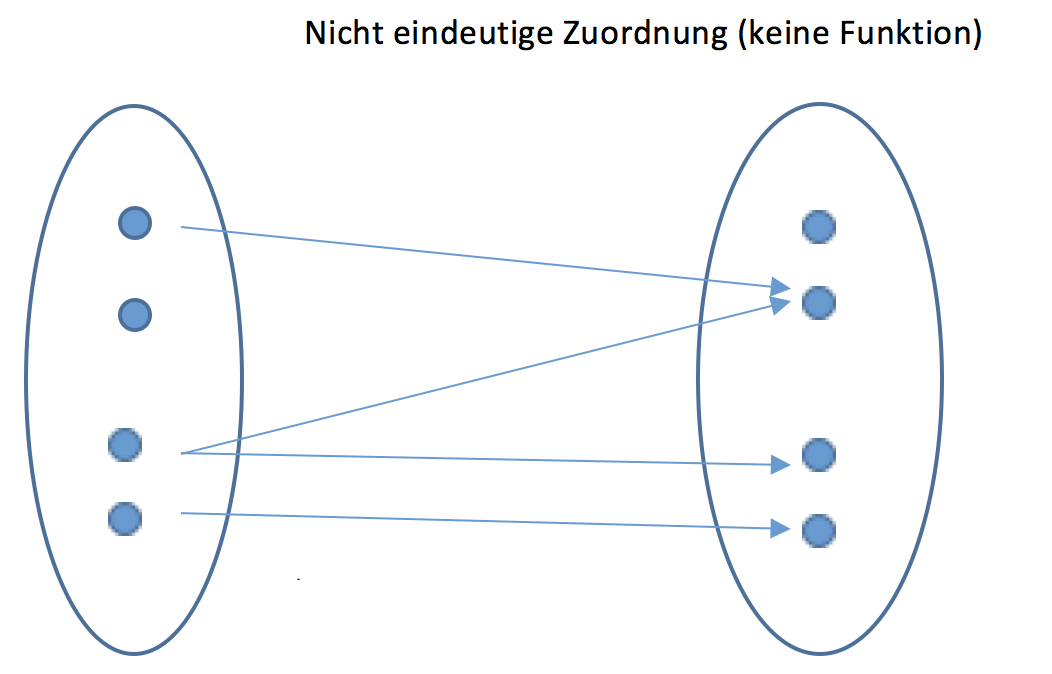
Beispiel:
In diesem Beispiel wird jeder natürlichen Zahl \(x\) ihr Quadrat \(y = f(x) = { x }^{ 2 }\) zugeordnet.
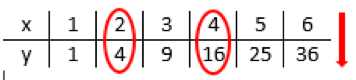
Definition 1 (Funktion)
Wenn zwei Größen so zusammenhängen, dass jedem Wert der ersten Größe genau ein Wert der zweiten Größe zugeordnet wird, dann nennt man diese Zuordnung Funktion.
Definition 2 (Funktion)
Seien A und B Mengen. Eine Zuordnung, die jedem Element der Menge A genau ein Element der Menge B zuordnet, nennt man Funktion.
Definition 3 (Funktion)
Eine Funktion f ist eine Teilmenge des kartesischen Produkts \(AxB\) zweier Mengen \(A\) und \(B\), bei der für alle \(x \in A\) genau ein \(y \in B\) existiert mit \((x, y) \in f\).

Darstellungen von Funktionen
Es gibt verschiedene Möglichkeiten eine Funktion darzustellen:
- graphische Darstellungen
- Tabellarische Darstellungen
- Darstellungen mit Termen
- verbale Darstellung, z.B. Verdopplung in 20 Minuten

Graphische Darstellungen:
Mit grafischen Darstellungen können funktionale Zusammenhänge visuell aufgezeigt werden. Im folgenden sind zwei Pfeildiagramme abgebildet. Diese stellen die Definitions- und die Zielmenge einer Funktion grafisch dar und drücken die Zuordnung von Elementen mithilfe von Pfeilen aus.
In der nebenstehenden Abbildung sehen Sie ein Pfeildiagramm zu einer Folge. In der unteren Graphik ist ein Pfeildiagramm zu Eigenschaften von Schüler:innen aufgezeigt.
Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2016). Didaktik der Analysis: Aspekte und Grundvorstellungen zentraler Begriffe. Heidelberg: Springer Spektrum, S. 54
Die gebräuchlichste grafische Darstellung von (reellen) Funktionen ist die Darstellung des Funktionsgraphen im kartesischen Koordinatensystem. Zu jedem Element \(x\) der Definitionsmenge gibt es ein Element \(y\) der Zielmenge mit \(y=f(x)\). Der Punkt \(x, y)\ liegt dann auf dem Funktionsgraphen. Beim Graphen handelt es sich, wie oben definiert, um eine Punktemenge, die die bekannte Kurven-Darstellung ergibt. Die Punkte haben die Form \((x,f(x))\).

Tabellarische Darstellungen
Eine sehr elementare Darstellung einer Funktion ist eine Wertetabelle. Diese stellt die einander zugeordneten Werte unmittelbar neben- bzw. untereinander dar. Die tabellarische Darstellungen von Funktionen hat offensichtlich Grenzen:
Wie bei Pfeildiagrammen können nur einzelne Wertepaare angegeben werden. Bei einer Funktion, die auf einer unendlichen Menge (z. B. einem Zahlenintervall) definiert ist, kann eine Tabelle also nur einen sehr kleinen Ausschnitt darstellen. Betrachtet man hier charakteristische Punkte, ist dies ein nützliches Hilfsmittel einen Graphen zu skizzieren. Darauf werden wir im nächsten Kapitel näher eingehen
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |

Darstellungen mit Termen
- Funktionsterm
\(f(x)=x^2+1\)
- Funktionsgleichung
\(y=x^2+1\)
- Zuordnungsvorschrift
\(x \mapsto x^2+1\)
Mit dem Term wird die Definitionsmenge für alle Elemente einheitlich festgelegt.

Aufgabe 1 - Darstellungswechsel:
- Ein Rechteck mit der Umfangslänge 24 cm ist x cm lang. Gib für seinen Flächeninhalt einen Funktionsterm und die Definitionsmenge an.
- Geben Sie eine Wertetabelle für \(f(x)=x^2+x \) an.
- Beschreiben Sie in Worten: \(f(t)=\frac{2t}{3}\)
Aufgabe 2:
Ergänzen Sie die folgende Tabelle:| Zahl | 3 | 11 | 27 | 64 | 89 | 111 | 127 | 567 | 625 |
| Quersummenwert | |||||||||
| Anzahl der Teiler |
Sind stellen die Zuordnungen Quersummenwert und Teilerzahl eine Funktion dar?
