Demokurs: Didaktik der Algebra
| Website: | WueCampus |
| Kurs: | vhb - Demokurs Lehramt |
| Buch: | Demokurs: Didaktik der Algebra |
| Gedruckt von: | Gast |
| Datum: | Sonntag, 15. Februar 2026, 00:23 |
1. Funktionen I


Funktionen sind der wichtigste Themenstrang im Algebraunterricht. Dabei bestehen enge Beziehungen zu den anderen Themensträngen.
In diesem Kapitel wird zunächst
- der Funktionsbegriff diskutiert.
- Der Umgang mit Funktionen und damit verbundene Denkweisen werden durch das Konzept des funktionalen Denkens fassbar.
- Dieses Denken entwickelt sich im Laufe der Kindheit und Jungend.
- Der Umgang mit Funktionen konkretisiert sich in verschieden funktionalen Darstellungen und dem Wechsel zwischen ihnen.

Allgemeiner Hinweis
Durch Anklicken der Graphiken am rechten Rand der Buchseiten bzw. aller blau markierten Texte öffnen sich Pop-Ups, die Beispiele, Aufgaben oder Erläuterungen enthalten.

1.1. Funktionsbegriff


Funktionen drücken Beziehungen zwischen Zahlen und Größen aus.

Hinsichtlich des Funktionsbegriffs kann man zwei Grundpositionen einnehmen:
1. Der Funktionsbegriff als Grundbegriff
Im Hinblick auf die grundlegende Bedeutung des Funktionsbegriffs wird empfohlen (BRÜNING, SPALLEK 1978), auf eine Definition zu verzichten und ihn stattdessen als eine eindeutige Zuordnung zu umschreiben.
Man nimmt damit eine gewisse Verschwommenheit in Kauf. Dafür lassen sich angemessene Vorstellungen aufbauen.
\[ f:A\to B \]
2. Funktionen als spezielle Relationen
PICKERT (1969) empfiehlt Funktionen als rechtseindeutige Relationen zu definieren.
Man gewinnt dabei eine präzise Grundlage, nimmt aber ein hohes Abstraktionsniveau in Kauf.
\[ f\subset A\times B \]

Als Kompromiss bietet sich ein genetischer Zugang an:
Hierbei wird zunächst auf eine Definition verzichtet und stattdessen erst Vorstellungen aufgebaut sowie Erfahrungen vermittelt. In einer Reflexionsphase kann dann der Funktionsbegriff kritisch hinterfragt werden, so dass das Bedürfnis nach einer formalen Definition bei den Lernenden geweckt wird.

Die beiden Grundpositionen finden sich in der historischen Entwicklung des Funktionsbegriffs wieder.

1.2. Aspekte des funktionalen Denkens


Die Unterrichtsreform zu Beginn des 20. Jahrhunderts erhielt mit dem etwas schillernden Begriff des funktionalen Denkens ein Schlagwort, das bis in unsere Zeit hineinwirkt. Es erstreckte sich auf alle Themenbereiche des Mathematikunterrichts, wirkte allerdings auch etwas verschwommen.
Eine Klärung versuchte VOLLRATH 1989:
Er versteht unter funktionalem Denken einen bestimmten gedanklichen Umgang mit Funktionen.
Dabei sind ihm drei grundlegende Sachverhalte wesentlich:
1. Der Zuordnungscharakter
Durch Funktionen beschreibt oder stiftet man Zusammenhänge zwischen Größen: Einer Größe ist dann eine andere zugeordnet, so dass die eine Größe als abhängig von der anderen gesehen wird.
2. Das Änderungsverhalten
Durch Funktionen erfasst man, wie sich Änderungen einer Größe auf die abhängige Größe auswirken.
3. Die Sicht als Ganzes
Mit Funktionen betrachtet man einen gegebenen oder gestifteten Zusammenhang als Ganzes.

Bei der Untersuchung funktionaler Zusammenhänge ist die Verbindung von Algebra und Geometrie sehr gewinnbringend. Folgende Aufgabe zeigt ein entsprechendes Beispiel. Die Fragen und Antworten zu Zusammenhängen lassen sich den Aspekten des funktionalen Denkens zuordnen.

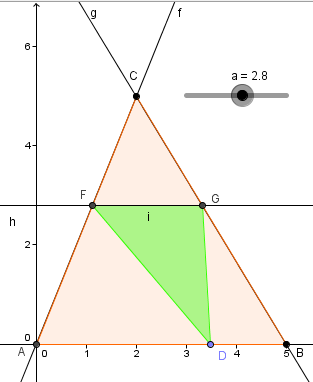
Aufgabe Dreieck im Dreieck
Gegeben sei Dreieck ∆ABC mit den Eckenpunkten A(0,0), B(5,0) und C(3,5). In diesem Dreieck ist ein kleines Dreieck ∆DGF einbeschrieben, dessen einer Eckpunkt D auf der Strecke [A,B] liegt. Die Parallele zur x- Achse mit der Funktionsgleichung \( h(x) = a \) für \( 0\le a\le 5 \) schneidet die Gerade f durch A und C im Punkt F und die Gerade g durch B und C im Punkt G.
- Änderungsaspekt: Wie ändert sich der Flächeninhalt A des kleinen Dreiecks bei Variation von a?
- Zuordnungsaspekt: In welchem Verhältnis steht der maximale Flächeninhalt des kleinen Dreiecks zum Flächeninhalt des großen Dreiecks?
- Objektaspekt: Durch welche Funktionsart lässt sich der Zusammenhang zwischen a und dem Flächeninhalt des kleinen Dreiecks beschreiben? Stellen Sie die Funktionsgleichung auf.

1.3. Entwicklung des Funktionalen Denkens


Funktionales Denken entwickelt sich. Das bedeutet insbesondere die Entwicklung folgender Fähigkeiten:
- Zusammenhänge zwischen Größen können festgestellt, angegeben, angenommen und erzeugt werden.
- Hypothesen über die Art des Zusammenhangs und über den Einfluss von Änderungen können gebildet, kontrolliert und gegebenenfalls revidiert werden.

Vor allem die Untersuchungen von PIAGET (Piaget u.a. 1977) haben Hinweise auf die Altersabhängigkeit dieser Fähigkeiten gegeben und im Hinblick auf die Erfassung proportionaler Zusammenhänge eine Fülle von Untersuchungen gebracht (s. Tourniaire/Pulos 1985).
Typische Entwicklungsstadien erkennt man am Fahrbahnversuch von VOLLRATH (1986):

Beim Fahrbahnversuch werden folgende Verhaltensmuster beobachtet:
(1) Ein Zusammenhang wird nicht erkannt.
Das Kind lässt die Kugel immer ganz oben starten. Auch die Misserfolge verändern das Verhalten nicht.
(2) Ein Zusammenhang wird angenommen, doch die Monotonie wird nicht erkannt.
Die Versuchsperson lässt die Kugel an verschiedenen Punkten starten. Es werden aber keine Konsequenzen aus dem Verhalten der Kugel gezogen.
(3) Die Monotonie des Zusammenhanges wird erkannt.
Die Versuchsperson erkennt: Je höher der Startpunkt liegt, desto weiter rollt die Kugel. Das führt dann durch systematisches Ändern der Ausgangsposition zum richtigen Startpunkt.
Das Stadium (3) wird im Alter von etwa 11-12 Jahren erreicht.

1.4. Darstellungen


Funktionen können in unterschiedlicher Weise dargestellt werden.
Zu den wichtigsten Darstellungsarten zählen:
1. Verbale Darstellung
Funktionale Zusammenhänge, insbesondere Abhängigkeiten und die Zuordnungsvorschrift, werden mit Worten beschrieben.
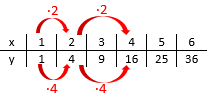
2. Numerische Darstellung als Tabelle
In einer tabellarischen Darstellung werden geordnete Wertepaare angegeben, sie gibt damit einen Überblick über die einander zugeordneten Zahlen.
Bei Funktionen mit unendlichem Definitionsbereich kann sie natürlich nur einen "Ausschnitt" der Funktion darstellen.
|
r |
0 |
1 |
2 |
3 |
4 |
|
U |
0 |
6.28 |
12.57 |
18.85 |
25.13 |
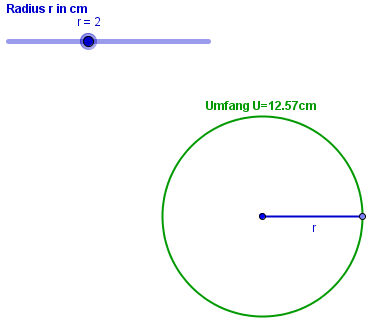
3. Graphische Darstellung als Graph oder Diagramm
Stellt man die Menge \( \{ (x; y)|y = f(x) \} \) im Achsenkreuz dar, so erhält man den Graphen der Funktion f. An ihm kann man leicht Eigenschaften der Funktion (Symmetrien, Periodizität, Proportionalität, …) erkennen.
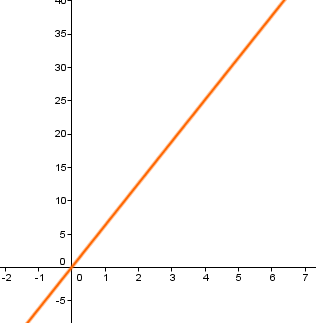
4. Symbolische Darstellung als (Funktions-) Term oder Gleichung
Die Beziehung zwischen der unabhängigen Variablen x und der abhängigen Variablen y wird als Gleichung angegeben. Bzw. man gibt den zur Variablen x zugeordneten Term an.
Termdarstellung \[ r\to 2\pi r \]


1.5. Aufgaben




- Geben Sie einige Beispiele, bei welchen geometrischen Themen der Sekundarstufe I der Funktionsbegriff mit Erfolg verwendet werden kann.
- Welchen Beitrag kann der Funktionsbegriff für fächerübergreifenden Unterricht zwischen Mathematik und Physik leisten?


Nennen Sie an geeigneten Beispielen einige wichtige Beiträge, die der Computer zum Verständnis und zur Beherrschung des Funktionsbegriffs leisten kann.