Demokurs: Didaktik der Analysis

Ein zentrales Ziel des Analysis-Unterrichts ist die Ausbildung von Grundvorstellungen, die der inhaltlichen Deutung mathematischer Begriffe dienen und deren Nutzen für Anwendungssituationen verdeutlichen.

Zu einer umfassenden Behandlung eines Begriffs und seiner Erfassung seiner Vernetzung mit anderen Begriffen der Analysis ist die Entwicklung verschiedener Vorstellungen notwendig.

Die Zugänge zum Ableitungsbegriff bauen jeweils primär auf einer der vorgestellten Grundvorstellungen auf (wobei stets Zusammenhänge zu den übrigen Vorstellungen bestehen).

Hier werden vor allem die zwei gängigsten unterrichtlichen Zugänge vorgestellt:

Zugang über lokale Änderungsraten

Dieser Zugang wird in den Bildungsstandards der KMK für das Abitur bevorzugt.

Hierbei wird auf die Beschreibung von Änderungs- oder Bewegungsprozessen zurückgegriffen, z.B. unter Betrachtung einer Funktion \(f \mapsto f(t)\), die jedem Zeitpunkt den zurückgelegten Weg zuordnet.

Die Frage nach der Momentangeschwindigkeit zu einem bestimmten Zeitpunkt \(t_0\) führt – aufbauend auf dem Geschwindigkeitsbegriff der Sekundarstufe I – zum Differenzenquotienten \(\left( \frac{\text{Weg}}{\text{Zeit}} \right) v = \frac{f(t) - f(t_0)}{t-t_0}, \; t\neq t_0\), der gerade der mittleren Änderungsrate, bzw. der physikalischen Durchschnittsgeschwindigkeit im Intervall \([t_0, t]\) entspricht.

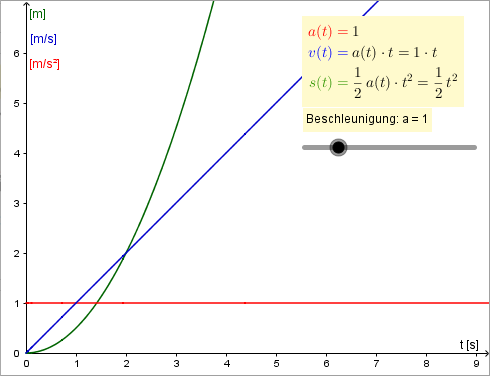
Exemplarisch lässt sich dieser Übergang anhand einer gleichmäßig beschleunigten Bewegung mit Beschleunigung \(a\) durchführen, deren zurückgelegte Strecke sich durch \(s(t) = \frac{1}{2}at^2\) beschreiben lässt.

Auch bei diesem Zugang lassen sich entsprechende Werte (in diesem Fall die Durchschnittsgeschwindigkeiten in immer kleiner werdenden Intervallen) mit einer Tabellenkalkulation aufzeigen; es kann beobachtet werden, dass sich diese Werte immer mehr dem einem bestimmten Wert annähern: der Momentangeschwindigkeit am Zeitpunkt \(t_0\), die der Ableitung von \(f\) entspricht.

Ermittlung der Durchschnittsgeschwindigkeit bei einer geradlinigen Bewegung mit der konstanten Beschleunigung  \(a\)

Zugang über Sekanten und Tangenten

Aufbauend auf der vorgestellten Grundvorstellung wird bei diesem Zugang eine Tangente an den Graphen einer Funktion angelegt. Dazu werden ein fester Punkt  \( P(x_0, f(x_0)) \) sowie ein beweglicher „Hilfspunkt“ \( Q(x_0+h, f(x_0 + h)), \; h\in\mathbb{R} \) gewählt. Durch \(P\) und \(Q\) wird eine Sekante gelegt und daraufhin  schrittweise verkleinert. Diese Situation kann mit Hilfe dynamischer Geometrie-Programme von den Lernenden erkundet werden und die Idee der Tangenten als Grenzlage von Sekanten kann dadurch zuerst auf graphischer Ebene erfahren werden.

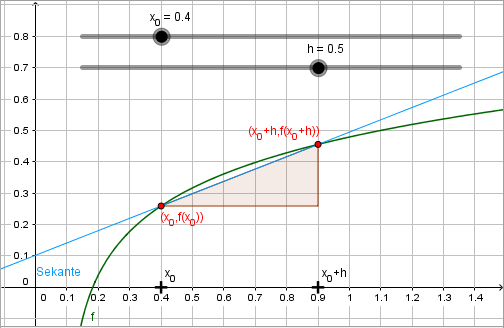
Die Sekantensteigung lässt sich (s. Definition) berechnen als \[ m_{PQ} = \frac{f(x_0 + h) - f(x_0)}{h}, \; h\neq 0 \]

Der Grenzprozess \(h\to 0\) kann nun graphisch, numerisch und symbolisch veranschaulicht werden.

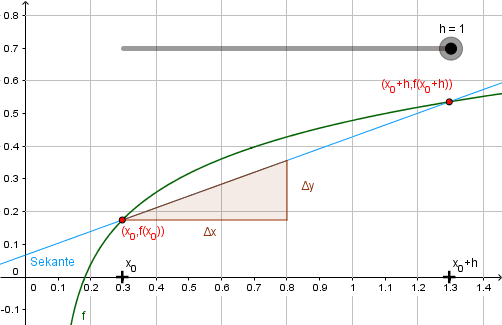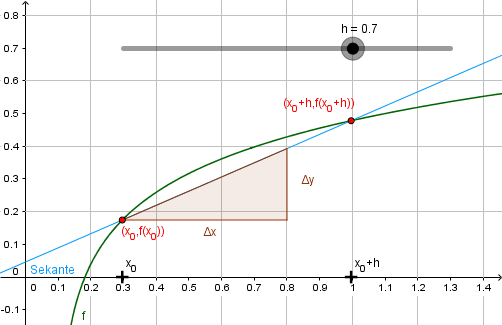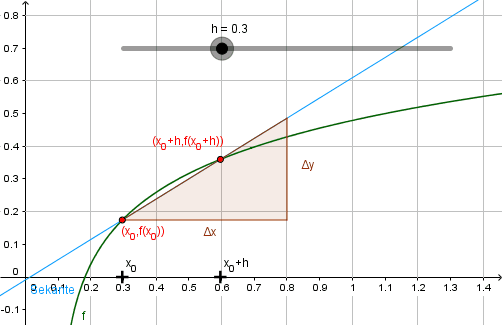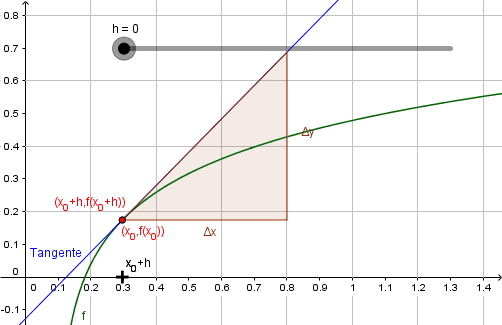
Die graphische Veranschaulichung lässt sich nur im Rahmen der Zeichengenauigkeit der verwendeten Software (oder einer klassischen Tafel) realisieren. Numerisch lässt sich der Grenzprozess ebenfalls nur diskret und bis zu einer gewissen Genauigkeit darstellen: 

Tabellarische Darstellung des Annäherungsprozesses in \(x_0 = 1\) für \(f(x)=\frac{1}{2}x^2\)

Auf der symbolischen Ebene lässt sich die Ableitung entsprechend der Definition als Grenzwert des Differenzenquotienten für \(h\to 0\) herleiten – beispielsweise ebenfalls anhand der Funktion \(f(x)=\frac{1}{2}x^2\): \[ \begin{align*} \frac{f(x_0 + h) - f(x_0)}{h}  &= \frac{\frac{1}{2}(x_0 + h)^2 - \frac{1}{2} {x_0}^2}{h} = \frac{\frac{1}{2} {x_0}^2 + x_0h + \frac{1}{2}h^2 - \frac{1}{2} {x_0}^2}{h} \\ &= x_0 + \frac{1}{2} h, \; h\neq 0 \end{align*}\]

Damit beträgt die Sekantensteigung für \(x_0 = 1\) gerade \(m=1 + \frac{1}{2}h\) und für den Grenzübergang \(h\to 0\) ergibt sich \(f'(x_0) = 1\).