Diagnostische Methoden IV: Schulleistungstests (Testbeispiele. Kennen lernen unterschiedlicher schulrelevanter Testtypen und ihrer Anwendungsbedingungen)

2.1.5 Die Normtabelle als ein zentrales Merkmal des normorientierten Schulleistungstests

Der bereits erwähnte Vergleich der Leistungen eines einzelnen Schülers mit dem anderer Schüler steht beim normorientierten Schulleistungstest auf stabilen Füßen. Aus Ergebnissen der großen Eichstichprobe errechnet der Testautor mit Hilfe eines der gängigen Statistikprogramme die Normtabelle. Dabei wird die empirische Verteilung der Eichstich-probe (Rohpunktverteilung) in die Normalverteilung überführt.

Unter Verwendung der Normtabelle ist der Testanwender nicht mehr nur auf die Rohpunktsumme angewiesen, welche, bei strenger Betrachtung, nur das Rangskalen-Niveau erreicht. Für den Anwender wichtig: Mit der Rohpunktsumme alleine kann keine Interpretation des individuellen Endergebnisses eines Schülers vorgenommen werden.

Ziel der statistischen Bearbeitung des Testautors und der Anwendung der Normtabelle durch den Testnutzer ist es, das Testergebnis in Standardwerte zu verwandeln und damit auf Intervallskalen-Niveau zu bringen (Lehreinheiten 4 und 5). Die für normorientierte Schul-leistungstests dabei eindeutig am meisten angewendete Skala ist die T-Skala mit dem Mittelwert von 50 und der Standardabweichung von 10 T-Punkten (s. Abb. 10.1). In Abbildung 10.1 sieht man auch, welchem Punkt der Normalverteilung ein T-Wert entspricht. Wenn ein Einzelergebnis (Rohwert) in einen T-Wert verwandelt ist, hat man mit diesem T-Wert gleich die interpretierbare Position des Schülers im gemessenen Merkmal, z.B. Rechtschreibfähigkeit im 5. Jahrgang Realschule.

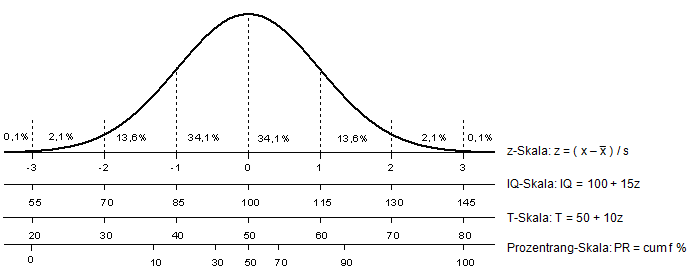
Abbildung 10.1: Vergleich verschiedener Standardwerte und ihre Relation zur Normalverteilung,  in Anlehnung an Michel & Conrad 1982, S. 78.

Nun gibt es außer dem T-Wert, in den sich die Nutzer erst einarbeiten müssen, noch eine andere Standardskala, nämlich die Prozentrangskala. Sie hat, wie der Name mitteilt, kein Intervallskalen-Niveau sondern eben nur das Rangskalen-Niveau, gleicht diesen Nachteil aber ein Stück weit durch ihre hohe Anschaulichkeit aus. So bedeutet etwa ein Prozentrangwert (PR) von 15:

In der Abbildung 10.1 ist auch die IQ-Skala (Intelligenzquotient) mit aufgenommen. Diese kann bei Schulleistungstests definitionsgemäß nicht angewendet werden. Es gibt aber Fragestellungen, bei denen es interessant ist, die Intelligenz und die Schulleistung eines Schülers in einem oder in mehreren Fächern zu vergleichen, so etwa im Fall des Underachievements, also der erwartungswidrigen Schlechten (wie L. Kemmler 1970 formulierte). Solange man an der sogenannten Diskrepanzdefinition der Legasthenie festhält (wie etwa im Bayerischen Legasthenie-Erlass), verlangt die damit einhergehende Definition zur Vergabe der Diagnose Legasthenie eine Diskrepanz der Rechtschreibleistung von der Intelligenzleistung. Die Rechtschreibleistung muss 10 oder 15 (in Bayern willkürlich auf 12 festgesetzt) T-Wert-Punkte (= eine ganze oder eineinhalb Standardabweichungen) unter dem gemessenen IQ liegen. Wenn man in Abbildung 10.1 den IQ durch eine senkrechte Linien-ziehung nach unten in den analogen T-Wert verwandelt, kann man prüfen, ob eine solche Diskrepanz vorliegt (zur Problematik der Diskrepanzdefinition s. Weber & Marx, 2008).

Die Anwendung der eigentlichen Normtabelle (Beispiel: s. Tabelle 10.3) geschieht nach folgendem einfachen Prinzip: Man lege ein Lineal quer über die Tabelle und schaue auf der dadurch entstehenden waagrechten Linie nach, welchem PR-Wert und welchem T-Wert der erreichte Rohpunktwert entspricht. Ein Ablesebeispiel: Dem Rohwert von 26 entsprechen in diesem Test ein PR-Wert von 31 und ein T-Wert von 45, der als "wahrer" Wert zwischen 43 und 48 liegt (zur Axiomatik der Klassischen Testtheorie s. Lehreinheit 3).

Ein Beispiel für eine Normtabelle (als Vorlage dient ein fiktives Beispiel mit maximal 44 möglichen Rohpunkten. Die Eichung wurde hier an 1 535 Schülern der angesprochenen Jahrgangsstufe durchgeführt). Mithilfe dieser Normtabelle kann man jeden vorkommenden Rohwert in einen Prozentrangwert oder einen T-Wert verwandeln. Das T-Wert-Band gibt das Vertrauensintervall an, innerhalb dessen der wahre Wert mit einer Wahrscheinlichkeit von p=0,.68 oder p=0,95 (oft nicht angegeben) liegt. 

Über den unten folgenden Link können Sie ein Video aufrufen, welches eine Musterlösung demonstriert.

https://wuecampus.uni-wuerzburg.de/moodle/mod/resource/view.php?id=186260

Geben Sie bitte einen Rohpunktwert ein und klicken Sie auf den Button "Lösung" um sich die referenzierten Werte anzeigen zu lassen.

Normtabellen eines Tests können auch getrennt für Untergruppen der Population angelegt werden. So kann man etwa denselben Rechtschreibtest für die 5. Jahrgangsstufe der Realschule und getrennt davon für die 5. Jahrgangsstufe des Gymnasiums normieren. Bei manchen normorientierten Schulleistungstests findet man auch zusätzlich zu der allgemeinen Normtabelle eigene Normtabellen für Jungen und Mädchen. Die Handhabung dieser so gewonnenen unterschiedlichen Standardwerte für Jungen und Mädchen darf nur mit großer Vorsicht vorgenommen werden.