Kapitel druckenKapitel drucken

Statistische Grundlagen der Diagnostik, Testtheorie

2. Verteilungen

Das in unserem Zusammenhang wichtigste Konzept der Statistik ist das der Verteilung. Misst man an einer Menge von Personen ein bestimmtes Merkmal, so ergibt sich eine Verteilung der gemessenen Werte. Da eine solche Verteilung empirisch erhoben wird, nennt man sie "empirische Verteilung". Es ist üblich, eine solche Verteilung grafisch in Form eines Säulendiagramms oder eines Histogramms darzustellen. Dazu teilt man den Bereich der gemessenen Werte in eine überschaubare Anzahl gleich großer Intervalle ein, die sich nicht überschneiden dürfen. Diese Intervalle werden auf der X-Achse abgetragen. Dann zählt man die Personen, deren Werte jeweils in einem Intervall liegen, und trägt die Anzahl als Säule auf der Y-Achse ab. An der Verteilungsgrafik kann man ablesen, über welchen Bereich sich die Messwerte erstrecken – man sagt auch, wie weit die Werte streuen – und welche Werte besonders häufig vorkommen.

Übung 1

Erstellung einer Verteilungsgrafik

Bearbeiten Sie die folgenden Übungsaufgaben.

  1. Laden Sie hier das Tabellenblatt herunter. Das Tabellenblatt enthält fiktive Daten, die man sich als Ergebnisse eines Tests vorstellen kann, bei dem maximal 75 Punkte erzielt werden können. Diese dienen als Grundlage der Bearbeitung.
  2. Sortieren Sie die Daten in aufsteigender Reihenfolge!
  3. Entscheiden Sie sich für geeignete Intervallgrenzen!
  4. Ordnen Sie den Rohwerten die entsprechende Nummer des Intervalls zu!
  5. Legen Sie eine Zeile mit Intervallbeschriftungen an!
  6. Zählen Sie die Fälle jeder Intervallnummer und tragen Sie das Ergebnis unter der Zeile mit den Beschriftungen ein! (Variante mit Funktion "zählenwenn")
  7. Markieren Sie die beiden Zeilen mit den Intervallbeschriftungen und den dazugehörigen Fallzahlen!
  8. Drücken Sie den Grafik-Button und folgen den Anweisungen des Diagramm-Assistenten!

 


Musterlösung

 Empirische Verteilungen haben häufig charakteristische Formen. So gibt es die meisten Fälle oft in der Mitte der Verteilung und die extremeren Werte verteilen sich in etwa symmetrisch um die Mitte herum. Eine solche Form nennt man auch "eingipfelig", wobei "Gipfel" das Intervall mit den meisten Fällen bezeichnet. Verteilungen, die dieser Form ähneln, können durch die statistischen Kennwerte Mittelwert und Standardabweichung gut beschrieben werden. Der Mittelwert einer Verteilung gehört zu den Maßen der zentralen Tendenz. Das gebräuchlichste unter diesen Maßen ist das arithmetische Mittel. Es wird gebildet, indem man alle Messwerte aufsummiert und durch die Anzahl der Fälle (meist Personen) teilt:

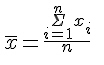
Gebräuchliche Abkürzungen für das arithmetische Mittel einer Verteilung sind (sprich "x quer"), M oder als sogenannter Populationsparameter µ (s.u.). Die Breite einer Verteilung wird durch sogenannte Dispersionsmaße beschrieben. Das zum arithmetischen Mittel gehörige Dispersionsmaß ist die Standardabweichung. Die Standardabweichung errechnet man, indem man die Summe der quadrierten Abweichungen jedes Messwertes vom Mittelwert durch die Anzahl der Fälle minus eins teilt und daraus die Wurzel zieht:

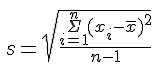
Die Standardabweichung ist aus einem weiteren wichtigen Maß, der Varianz, abgeleitet. Die Berechnung der Varianz entspricht der der Standardabweichung, nur dass die Wurzelziehung wegfällt; die Varianz ist also gleich der Standardabweichung zum Quadrat. Sie wird entsprechend meist mit s2 bezeichnet. Varianzen sind von den Zahlenwerten weniger anschaulich als Standardabweichungen, haben aber vorteilhafte mathematische Eigenschaften, die für Berechnungen genutzt werden.


Übung 2

Berechnung des Mittelwertes und der Standardabweichung mit Tabellenkalkulation

Bearbeiten Sie die folgenden Übungsaufgaben.

  1. Öffnen Sie die vorher bearbeitete Datei Diag03-UeA01-Daten.xls!
  2. Gehen Sie in die Zelle B78 und geben "=" ein! (Damit weiß das Programm, dass Sie eine Funktion oder Formel eingeben wollen).
  3. Schreiben Sie "mittelwert("!
  4. Markieren Sie die ganze Zahlenreihe in Spalte B!
  5. Geben Sie ")" und Enter ein! Nun erscheint in Zelle B78 der Mittelwert der Datenreihe.
  6. Beschriften Sie das Feld durch Eingabe von "M" in Zelle A78! (Beschriftungen sind wichtig, um sich später auf Kalkulationsblättern wieder zurechtzufinden.)
  7. Wiederholen Sie das Vorgehen in Zelle B79, um die Standardabweichung zu berechnen. Die zugehörige Funktion heißt "stabw(<Bereich>)"

Musterlösung

Theoretische Überlegungen zu den stochastischen Prozessen (Zufallsprozessen), die empirischen Verteilungen zugrunde liegen, führen zu theoretischen Verteilungen. Die bekannteste davon ist die Normalverteilung. Theoretisch folgt die Verteilung eines Merkmals dann der Normalverteilung, wenn es von mehreren, unabhängig voneinander variierenden Einflussfaktoren abhängt. Man spricht dann auch davon, dass das Merkmal normalverteilt sei.


Übung 3

Verteilung der Summe von Würfen mit 5 Würfeln

Abbildung 3.1: Verteilung in Form eines Histogramms


Die Normalverteilung ist durch die beiden Parameter Mittelwert und Standardabweichung vollständig festgelegt. Das bedeutet, dass Normalverteilungen mit unterschiedlichen Mittelwerten und Standardabweichungen recht unterschiedlich aussehen können. Sie können dies mit dem Applet "Normalverteilung" nachvollziehen. Bei der Darstellung von theoretischen Verteilungen wird die jeweilige Merkmalsausprägung auf der X-Achse abgetragen. Auf der Y-Achse wird die sogenannte Dichte dargestellt. Vereinfacht ausgedrückt entspricht die Dichte der erwarteten Häufigkeit von Fällen1.


Übung 4

Normalverteilung

Eine praktisch sehr bedeutsame Eigenschaft der Normalverteilung ist, dass man für alle Intervalle von Merkmalsausprägungen genau berechnen kann, welcher Anteil von Fällen innerhalb des Intervalls zu erwarten ist. Formal wird dazu das Integral der Dichtefunktion zwischen den Intervallgrenzen berechnet. Da das Integral anschaulich der Fläche unter der Dichtekurve entspricht, ist der erwartete Anteil von Fällen gleich dem Verhältnis der Fläche innerhalb der Intervallgrenzen zur Gesamtfläche unterhalb der Dichtekurve.

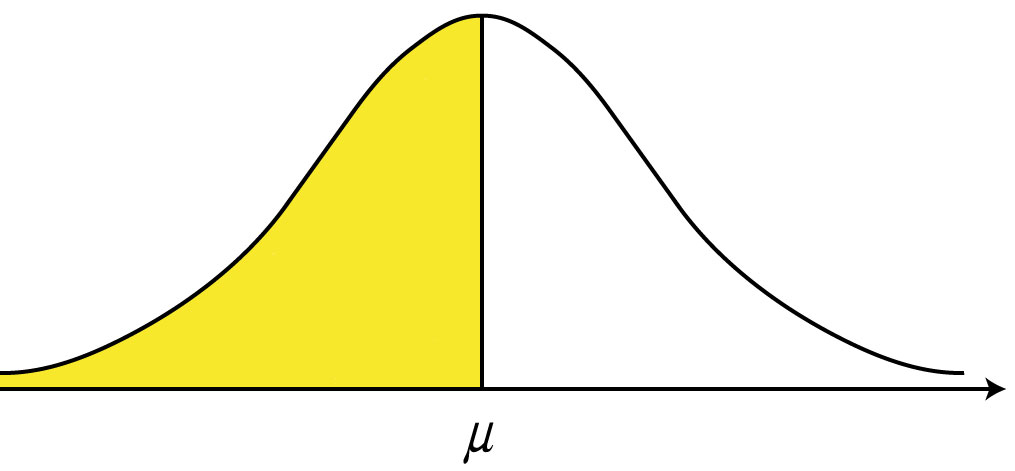
Abbildung 3.2: Integral unter einer NV-Kurve


Wir wollen dies am Beispiel der theoretischen Verteilung des Intelligenzquotienten nachvollziehen. Diese entspricht einer Normalverteilung mit einem Mittelwert von 100 und einer Standardabweichung von 15. Man kann nun angeben, welcher Anteil von Fällen mit einem IQ zwischen 100 und 115 zu erwarten ist: Es sind rund 34%. Fälle mit einem IQ größer als 130 sind dagegen nur 2,3% zu erwarten. Die erwarteten Häufigkeitsanteile der Abschnitte, die durch Vielfache der Standardabweichung gebildet werden, sind in Abbildung 3.4 angegeben.

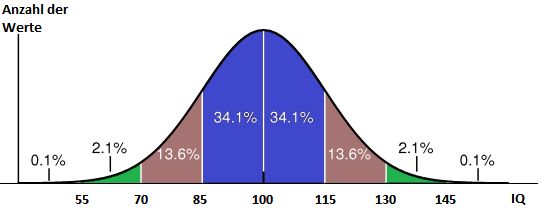
Abbildung 3.3: Anteile unter der NV-Kurve


In der Praxis muss man allerdings keine Integrale berechnen, sondern kann die entsprechenden Werte in Tabellen ablesen. Dazu wird die konkret vorliegende Verteilung per linearer Transformation in die Standardnormalverteilung umgerechnet, deren Mittelwert bei 0 und deren Standardabweichung bei 1 liegt. Da die Flächenverhältnisse unter der Dichtekurve von linearen Transformationen des Merkmals nicht verändert werden, ist dies ohne Informationsverlust möglich. Die Werte der Merkmalsausprägung werden also in sogenannte z-Werte umgerechnet und zwar nach folgender Formel:

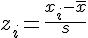
Man bezeichnet dies auch als z-Transformation. In Tabellen zur Standardnormalverteilung ist für jeden z-Wert der Flächenanteil unterhalb der Dichtekurve von minus unendlich bis zum jeweiligen z-Wert angegeben.

Etwas Ähnliches geschieht auch bei der Berechnung von Intelligenzquotienten. Da die Rohpunktwerte von Intelligenztests nicht so verteilt sind, dass sich im Mittel 100 Punkte ergeben, werden sie so transformiert, dass sich ein Mittelwert von 100 und eine Standardabweichung von 15 ergibt.

Neben der Normalverteilung gibt es eine Reihe weiterer theoretischer Verteilungen, wie etwa die Binomialverteilung, die die Verteilung von positiven Ausgängen binärer Ereignisse beschreibt, oder die Chi-Quadrat-Verteilung der Summe von n stochastisch unabhängigen, quadrierten normalverteilten Zufallsvariablen. Diese Verteilungen können aber im Rahmen des vorliegenden Kurses nicht besprochen werden. Stattdessen soll hier ein häufiges Missverständnis angesprochen werden: Es besteht in der Annahme, dass Schulleistungen, also auch die Ergebnisse von Klassenarbeiten, innerhalb einer Klasse normalverteilt sein sollten. Dies ist aus zwei Gründen falsch. Erstens sind bei Stichprobengrößen von etwa 30 Personen oder weniger deutliche Abweichungen der empirischen Verteilung von der theoretischen Verteilung wahrscheinlich. Das heißt, dass selbst wenn in der Population (also z.B. alle Neuntklässler in bayerischen Gymnasien) das Merkmal normalverteilt wäre, kann man für kleine, nicht zufällig gezogene Teilstichproben (Klassen) keineswegs erwarten, dass das Merkmal auch dort der Normalverteilung folgt. Dies liegt daran, dass nach dem Gesetz der großen Zahl Schätzungen statistischer Kennwerte – wozu man auch Verteilungen rechnen kann – erst bei größeren Stichproben genauer werden.

Zweitens ist es keineswegs immer sinnvoll, für Schulleistungen die Normalverteilung zu erwarten. Wenn ein Test beispielsweise zur Lernzielkontrolle durchgeführt wird, sollten die Ergebnisse hauptsächlich von einem Faktor – dem Unterricht – abhängen und nicht von einer Vielzahl zufällig variierender Einflussfaktoren. Wenn der Unterricht gut war, kann man durchaus Verteilungen erwarten, die deutlich in Richtung guter Leistungen verschoben sind.

Neben den gebräuchlichen Verteilungskennwerten arithmetisches Mittel und Standardabweichung gibt es weitere Kennwerte, die vor allem dann verwendet werden, wenn Daten vorliegen, die nicht auf Intervallniveau interpretiert werden dürfen. Auf die Datenniveaus werden wir in Kapitel 5 noch zu sprechen kommen. Hier seien vorerst nur die Maße kurz beschrieben: Der Median (Mdn) ist ein Maß der zentralen Tendenz, der gewissermaßen die Verteilung in zwei Hälften teilt. Ordnet man alle n Meßwerte einer Stichprobe der Größe nach, so entspricht der Wert an der Stelle n/2 dem Median. Das dazugehörige Dispersionsmaß ist der Quartilabstand; das ist die Differenz zwischen den Werten an den Stellen ¼ n und ¾ n. Bei Häufigkeitsverteilungen über Kategorien (also z.B. Berufe oder Länder) ist der Modalwert als Maß der zentralen Tendenz anzusehen. Er ist gleich dem Namen der Kategorie mit den meisten Fällen.

1 Streng genommen sind bei stetigen Zufallsvariablen Wahrscheinlichkeiten für das Auftreten einzelner Werte nicht ermittelbar, da es ja unendlich viele Möglichkeiten für einzelne Werte gibt. Es ist allerdings möglich, solche Wahrscheinlichkeiten für Intervalle von Werten anzugeben. Dies wird mit der Verteilungsfunktion ausgedrückt, die für jeden möglichen Wert die Wahrscheinlichkeit wiedergibt, dass der Wert mindestens so groß ist. Die Dichte entspricht demgemäß der ersten Ableitung der Verteilungsfunktion.