Kegelschnitte
2.1 Drehungen in Ebene und Raum
In diesem Kapitel fokussieren wir uns auf Drehungen, Spiegelungen und Drehspiegelungen von geometrischen Objekten. Für deren Beschreibung benötigen wir sogenannte orthogonale Abbildungen (bzw. orthogonale Matrizen). Kurz gesagt bilden orthogonale Abbildungen 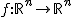 orthogonal zu einander stehende Vektoren wieder auf orthogonale Vektoren ab. |