Wir wollen zwei geometrische Objekte als nicht wesentlich verschieden ansehen, wenn sie sich zwar durch ihre Lage im Raum, nicht aber in Form und Größe unterscheiden, bzw. mathematisch präziser: wenn sie sich durch sogenannte euklidische Bewegungen ineinander überführen lassen. Euklidische Bewegungen sind hierbei abstandserhaltende Abbildungen 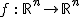 . Sie bestehen aus einer orthogonalen Abbildung verkettet mit Translationen und sind somit linear und winkeltreu. . Sie bestehen aus einer orthogonalen Abbildung verkettet mit Translationen und sind somit linear und winkeltreu. |