Demokurs: Mathematik und Computer

Der Zugmodus

In dieser Einheit lernen Sie den Zugmodus kennen. Dieser ist für die "Dynamik" der DGS verantwortlich und stellt eine Erweiterung zu den herkömmlichen Zirkel- und Linealoperationen dar. Dies wird z.B. an folgender Beispielaufgabe deutlich:

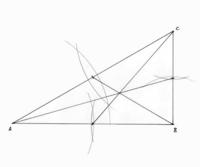
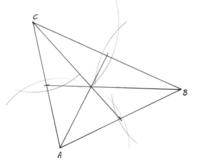
Es sollen alle drei Seitenhalbierenden eines Dreiecks konstruiert werden.
Die Konstruktion kann mit Zirkel und Geodreieck auf Papier angefertigt werden. Stellt man sich die Lösung in Form einer solchen Papierzeichnung vor, so könnte das Ergebnis aussehen, wie rechts dargestellt.

Es sieht so aus, als würden sich die Seitenhalbierenden in einem Punkt schneiden. Um festzustellen, ob es sich nicht nur um einen "Zufall" handelt, müssten zunächst mehrere weitere Zeichnungen angefertigt werden:

Wie man sieht, schneiden sich die Seitenhalbierenden anscheinend in allen Fällen in einem Punkt.

Mit Hilfe des Zugmodus ist die Veränderung der Lage von Punkten auf dem Bildschirm möglich. Vom Computer wird dabei sofort die neue Lage aller von diesem Punkt abhängigen Objekte berechnet und am Bildschirm neu dargestellt. Die ursprünglichen Beziehungen zwischen den geometrischen Objekten bleiben dabei erhalten.

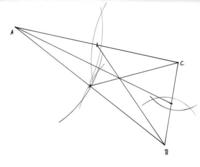
Beispiel 2:

Gegeben sind ein Dreieck ABC und dessen Seitenhalbierenden. Nutzen Sie den Zugmodus um verschiedene Lagen des Dreiecks zu erhalten! Was fällt Ihnen auf?

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Die Vermutung, dass sich die Seitenhalbierenden in jedem Fall in einem Punkt schneiden, kann durch den Zugmodus an "sehr vielen" Beispielen nachvollzogen werden.
Zur Bestätigung dieser Vermutung ist allerdings ein mathematischer Beweis erforderlich. Einen Beweis finden sie z.B. hier.

Aufgabe 1:

Konstruieren Sie ein Dreieck und einen entsprechenden Umkreis. Benutzen Sie dazu den Schnittpunkt von zwei Mittelsenkrechten.
Eine Schritt für Schritt-Anleitung finden Sie hier.

Aufgabe 2:

Zeichnen Sie mit einem DGS einen Halbkreis und ein Dreieck, um den Satz des Thales zu veranschaulichen. Fügen Sie die Winkel ein.